Как часто хочется себе представить как движения планет зависят от звезды? Сегодня для этого не нужен телескоп! Представить движения планет в зависимости от объекта очень большой массы можно и на компьютере.
Идея для данной программы зародилась в момент, когда я захотел наглядно представить себе то, как движутся планеты нашей солнечной системы, и как бы менялась траектория движения планет относительно солнца при различных начальных условиях.
Долго тянуть не буду и сразу перейду к краткому описанию программы. Решил писать на питоне. Суть заключается в том, что мы можем создавать планеты в любой точке плоскости, с любым радиусом, массой, цветом и начальной скоростью и моделировать их взаимодействие.Чтобы было не очень сумбурно, решил в куски с кодом вставлять комментарии.
Сначала продемонстрирую пример работы: создаю Солнце и 6 планет, левым придаю скорость вверх, а правым - вниз, равную по модулю. Несмотря на то, что в начальный момент скорость каждой из планет одинакова, свой полный оборот вокруг Солнца они завершают в разное время. Это происходит из-за разницы в начальных расстояниях.



Первый блок: просто импортируем необходимые библиотеки
import pygame
import timeВторой блок: создаём необходимые переменные
fps = 120 # просто fps
G = 6.67 / 10 ** 11 # сохраняем константу гравитационной постоянной
k = 1000000 # метров в одном пикселе
mouse_x, mouse_y = 0, 0 # начальное положение мышки (начальные значения не очень влияют)
time_speed = 10000 # коэффициент ускорения программы
# При коэффициенте ускорения больше 10 ^ 5, появляется очень большая погрешностьТретий блок: запускаем окно, задаём ширину, высоту и переменные для отображения fps и ускорения
pygame.init()
screen = pygame.display.set_mode((1500, 800))
pygame.display.set_caption("Planetary acceleration")
style = pygame.font.SysFont("arial", 36)
render_fps = style.render('fps ' + str(fps), True, 'blue')
render_time_speed = style.render('acceleration: ' + str(time_speed), True, 'blue')Четвёртый блок: для удобства создадим класс, который будет отвечать за одну планету
class Planet:
def __init__(self, x, y, r, m, color): # задаём начальные параметры
self.x = x # координата по оси Ох
self.y = y # координата по оси Оу
self.r = r # радиус планеты
self.m = m # масса планеты
self.color = color # цвет планеты
self.speed = [0, 0] # скорость которую имеет планета
self.f = [0, 0] # сила, которые действуют на планету
self.status = True # существует планета или уже нет
self.trace_count = 0 # переменная, чтобы "не очень часто" выводить траекторию планеты, иначе сильно упало бы fps
self.trace = [] # точки траектории нашей планеты
def update_coordinates(self): # обновляем скорость, координату и траекторию
self.speed[0] += (self.f[0] / self.m) * time_speed ** 2 / fps ** 2
self.speed[1] += (self.f[1] / self.m) * time_speed ** 2 / fps ** 2
self.x += self.speed[0]
self.y += self.speed[1]
self.trace_count += (self.speed[0] ** 2 + self.speed[1] ** 2) ** 0.5
if self.trace_count / k >= 7: # чем меньше число после знака, тем более сплошной будет траектория при выводе
self.trace_count = 0
self.trace.append((self.x, self.y))
if len(self.trace) > 1000: # Также, чтобы не проседало fps, когда много точек, начинаем удалять с конца
self.trace.pop(0)
def draw(self): # отображаем все планеты и их траектории
pygame.draw.circle(screen, self.color, ((self.x - mouse_x) / k, (self.y - mouse_y) / k), self.r / k)
for i in self.trace:
pygame.draw.circle(screen, self.color, ((i[0] - mouse_x) / k, (i[1] - mouse_y) / k), 1)Пятый блок: нужен для определения всех сил, действующих на каждую планету
def update_forces(planets, collides):
for i in range(len(planets)):
for j in range(i + 1, len(planets)):
dif_x = planets[j].x - planets[i].x # разница между двумя планетами по х
dif_y = planets[j].y - planets[i].y # разница между двумя планетами по y
d = (dif_x ** 2 + dif_y ** 2) ** 0.5 # пифагорово расстояние между планетами
f = G * planets[i].m * planets[j].m / d ** 2 # Сила между двумя планетами
planets[i].f[0] += dif_x * f / d # обновляем действующие силы на тело
planets[i].f[1] += dif_y * f / d
planets[j].f[0] -= dif_x * f / d
planets[j].f[1] -= dif_y * f / d
if planets[i].r + planets[j].r > d: # Находим какие две планеты сталкиваются друг с другом
collides.append((i, j))Шестой блок: обрабатываем все столкновения планет
def remove_collides(planets, collides):
for i in collides:
p1 = planets[i[0]]
p2 = planets[i[1]]
if p1.status and p2.status: # если обе планеты ещё существуют
if p1.m > p2.m: # какая планета больше по массе, та и выиграла
new_planet = Planet(p1.x, p1.y, p1.r + p2.r, p1.m + p2.m, p1.color)
else:
new_planet = Planet(p2.x, p2.y, p1.r + p2.r, p1.m + p2.m, p2.color)
new_planet.speed = [(p1.m * p1.speed[0] + p2.m * p2.speed[0]) / (p1.m + p2.m),
(p1.m * p1.speed[1] + p2.m * p2.speed[1]) / (p1.m + p2.m)]
planets.append(new_planet)
p1.status = p2.status = 0Седьмой блок: для примера, создаём солнце и несколько планет
planets = []
# Солнце
p = Planet(0, 0, 696_000_000, 1.9891 * 10 ** 30, 'orange')
planets.append(p)
for i in range(14, 20):
p = Planet((-1) ** i * (i * 10 ** 9 + 10 ** 9), 0, 1, 1, 'green')
planets.append(p)
planets[i - 13].speed[1] += (-1) ** i * 29273.6 * time_speed / fpsВосьмой блок: запускаем основную программу, обрабатываем все команды, которые могут поступать от пользователя и обновляем массив, в котором содержаться ещё "живые" планеты
tick = 0
tm = time.time()
running = True # стандартная переменная для запуска цикла
while running:
tick += 1
if tick == 100: # чтобы fps в левом углу не сходил с ума и не происходило деление на ноль
tick = 0
render_fps = style.render("fps:" + str(int(100 / (time.time() - tm))), True, "blue")
tm = time.time()
for event in pygame.event.get(): # начинаем обрабатывать команды
if event.type == pygame.QUIT: # выход
running = False
if event.type == pygame.MOUSEBUTTONDOWN: # нажатие любой кнопки мыши
x = event.pos[0] # определяем где находится мышка у пользователя
y = event.pos[1]
new_x = mouse_x + x * k # считаем коэффициенты для в нашей "размерности"
new_y = mouse_y + y * k
if event.button == 4: # колёсико мышки вперёд - приближение космической карты
k *= 0.85
mouse_x = new_x - x * k
mouse_y = new_y - y * k
if event.button == 5: # колёсико мышки назад - отдаление космической карты
k /= 0.85
mouse_x = new_x - x * k
mouse_y = new_y - y * k
if event.button == 3: # правая кнопка мыши - добавляем планету в точку, куда указывает мышка
planets.append(Planet(new_x, new_y, 6371000, 5.9722 * 10 ** 24, 'blue'))
if event.button == 2: # нажатие колёсика - ускорение работы программы
if time_speed >= 100000:
time_speed = 1
for i in planets:
i.speed[0] /= 100000 # уменьшение скоростей планет
i.speed[1] /= 100000
else:
time_speed *= 10
for i in planets:
i.speed[0] *= 10
i.speed[1] *= 10
render_time_speed = style.render('acceleration: ' + str(time_speed), True, 'blue') # обновляем отображение ускорения
if event.type == pygame.MOUSEMOTION: # для перемещения по космической карте с помощью удержания левой кнопки мыши
if pygame.mouse.get_pressed()[0]:
mouse_x -= event.rel[0] * k
mouse_y -= event.rel[1] * k
collides = [] # массив для определения кортежей столкновений
update_forces(planets, collides) # находим все столкновения
remove_collides(planets, collides) # обрабатываем все столкновения
screen.fill("black") # обновляем чёрный фон
new_planets = []
for planet in planets:
if planet.status: # выбираем только те планеты, которые ещё не столкнулись
planet.update_coordinates() # обновляем их значения
planet.f = [0, 0] # сбрасываем действующие силы
new_planets.append(planet) # сохраняем "живые" планеты
planet.draw() # отображаем всё
planets = new_planets # обновляем массив
screen.blit(render_fps, (10, 10)) # выводим fps
screen.blit(render_time_speed, (10, 50)) # выводим ускорение
pygame.display.update()
pygame.quit() # заканчиваем Всё. Это вся программа, которая необходима для данной задачи.
Под конец, давайте полностью смоделируем работу Солнечной системы!
Добавим код для создания Солнца и всех планет
# Земля:
p = Planet(-152 * 10 ** 9, 0, 6371000, 5.9722 * 10 ** 24, 'green')
planets.append(p)
planets[0].speed[1] += 29273.6 * time_speed / fps # скорость вокруг солнца
# Луна:
p = Planet(-363104000 - 152 * 10 ** 9, 0, 1737100, 7.35 * 10 ** 22, 'grey')
planets.append(p)
planets[1].speed[1] = 1023 * time_speed / fps # скорость вокруг земли
planets[1].speed[1] += 29273.6 * time_speed / fps # скорость вокруг солнца
# Меркурий
p = Planet(-69.8 * 10 ** 9, 0, 2439700, 3.33022 * 10 ** 23, "yellow")
planets.append(p)
planets[2].speed[1] += 38000 * time_speed / fps # Скорость вокруг солнца
# Венера
p = Planet(-109 * 10 ** 9, 0, 6051800, 4.8675 * 10 ** 24, "white")
planets.append(p)
planets[3].speed[1] += 34000 * time_speed / fps
# Марс
p = Planet(-249.2 * 10 ** 9, 0, 3390000, 6.4171 * 10 ** 23, "red")
planets.append(p)
planets[4].speed[1] += 23000 * time_speed / fps
# Юпитер
p = Planet(-816.521 * 10 ** 9, 0, 71492000, 1.8986 * 10 ** 27, "brown")
planets.append(p)
planets[5].speed[1] += 12500 * time_speed / fps
# Сатурн
p = Planet(-1.51 * 10 ** 12, 0, 60268000, 5.6846 * 10 ** 26, "beige")
planets.append(p)
planets[6].speed[1] += 9100 * time_speed / fps
# Уран
p = Planet(-3 * 10 ** 12, 0, 25362000, 8.6813 * 10 ** 25, "pink")
planets.append(p)
planets[7].speed[1] += 6300 * time_speed / fps
# Нептун
p = Planet(-4.5 * 10 ** 12, 0, 24622000, 1.02409 * 10 ** 26, "blue")
planets.append(p)
planets[8].speed[1] += 4950 * time_speed / fps
# Солнце
p = Planet(0, 0, 696_000_000, 1.9891 * 10 ** 30, 'orange')
planets.append(p)В связи с тем, что расстояние между планетами очень большое, сначала я решил показать симуляцию движения планет земного типа
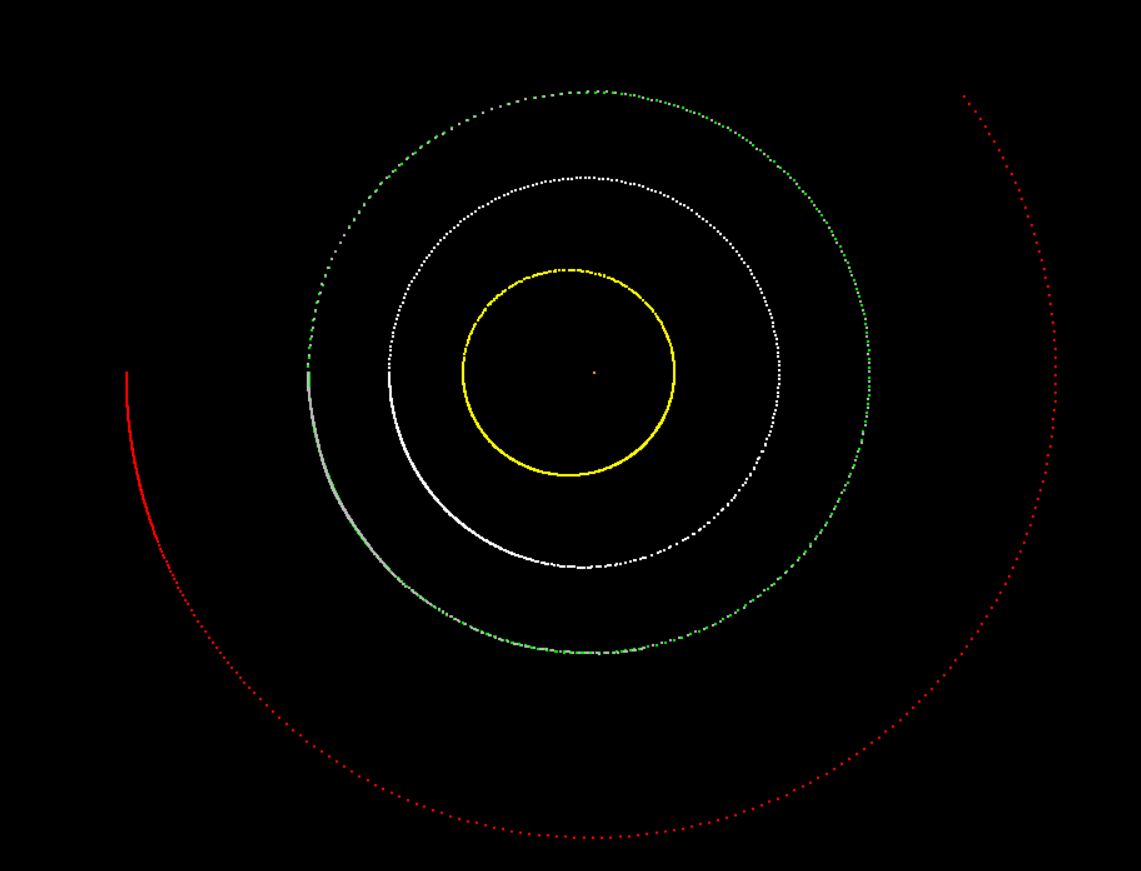
Теперь немного отдалимся от Солнца и посмотрим на оставшиеся планеты

Это всё, что я хотел рассказать и показать вам сегодня. Смело копируйте программу и проводите свои собственные эксперименты на космической карте!
Комментарии (31)

belch84
20.08.2023 12:23Вот относительно простая гравитационная система (гипотетическая) двух тел, для различных соотношений их масс траектории одного из тел могут быль существенно разными
Задача двух тел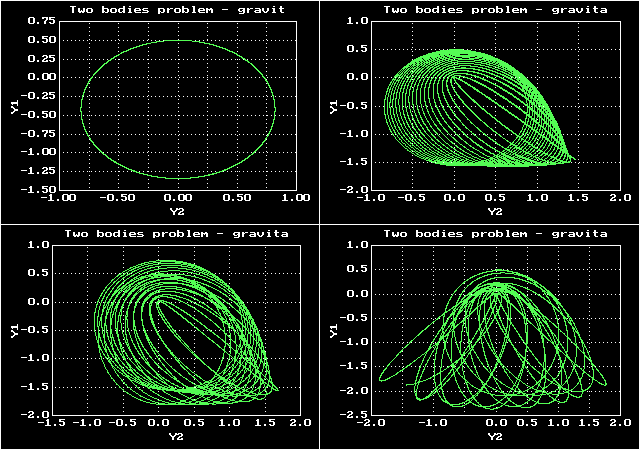
Здесь метод интегрирования намного более точный, чем метод Эйлера (а именно — метод Рунге-Кутты порядка 4 с переменным шагом), а траектория может быть как очень простой, так и достаточно сложной



Smog1on1the1water
Не буду комментировать код, прокомментирую сам подход.
1. При выполнении симуляций физических моделей уравнения принято обезразмеривать. Все эти размерные величины в ходе итераций не нужны от слова вовсе и лишь усложняют вычисления, так как на каждом шаге вы делаете лишние телодвижения, это не эффективно и излишне.
2. В вашей симуляции все планеты будут двигаться по спиралям, а не по замкнутым эллиптическим орбитам. Причина - использование метода Эйлера, который является простейшим из численных методов. Вы отрезок эллипса заменяете на небольшой кусочек прямой, но не делаете никакой коррекции на изменение угла. В результате, на каждом шаге будет накапливаться расхождение (Ломаная Эйлера и точное решение задачи), и в итоге планеты у вас постоянно будут разлетаться, система не проживет и тысячи лет. Это самая грубая ошибка, которую вы могли допустить.
3. Вместо метода Эйлера в данном случае не обязательно использовать методы прямо более высоких порядков, но хотя бы модифицированный метод Эйлера был бы гораздо лучше.
4. При выполнении симуляций строго необходимо контролировать базовые параметры системы на предмет корректности. В данном случае - закон сохранения энергии. Нужно постоянно (не обязательно на каждой итерации, но достаточно регулярно) вычислять энергию системы и следить, чтобы она не менялась (гравитационных волн у вас нет). Вы этого не сделали, поэтому ошибки остались незамеченными.
Список замечаний не полный, но для начала хватит.
Z1at Автор
Спасибо большое за все замечания! Если буду дальше модифицировать программу, постараюсь учесть все замечания, в частности закон сохранения энергии.
Только не совсем понял по поводу второго пункта. Ведь на самом первом примере видно, что если создать одно тело, масса которого сильно превышает все остальные, то оставшиеся тела будут как раз вращаться по эллиптическим орбитам. Конечно, небольшое расхождение будет, но сомневаюсь, что настолько большое, чтобы тела начали двигаться с большим отклонением от оригинальной орбиты.
Pavgran
Зря сомневаетесь. Система тел под влиянием гравитации - хаотическая система. Малые возмущения приводят к большим изменениям в траекториях. В том числе и небольшие погрешности метода интегрирования будут накапливаться и приведут к большим изменениям в окончательных траекториях. Попробуйте сравнить точное решение задачи двух тел (Солнца и Юпитера, например) с результатом вашей симуляции после, скажем, 10 миллионов шагов.
ред.: Вообще говоря, система из двух тел не хаотична, хаос начинается с трёх тел. И мой аргумент с предложением сравнения модели и точного решения не совсем последователен с предыдущим аргументом про хаотичность гравитации. Но увидеть расхождение можно будет все равно, поскольку сам прямой метод Эйлера расходится.
belch84
Pavgran
Хм, спасибо, буду знать.
Smog1on1the1water
Вообще показано, что динамика тел в Солнечной системе таки является хаотической, см. Laskar 1989, 1990. Фазовые траектории системы расходятся экспоненциально. Поэтому на масштабе порядка нескольких десятков миллионов лет моделирование астрономических факторов изменения климата (в целях палеоклиматических исследований) теряет смысл, увы.
belch84
Численные решения для внешних планет
Smog1on1the1water
Во-первых, русская Википедия - это плохой источник. Она нерегулярно обновляется и качество статей по физике в ней невысоко. Во-вторых, именно в данном случае в оригинальной статье, на которую ссылается русская Вики, говорится, что there exist clearly chaotic trajectories with complex structure and Lyapunov times-the timescale for the onset of chaos-ranging from 2million years to 230million years, as well as trajectories that show no evidence of chaos over 1Gyr timescales. Совсем не то же самое, что написано в русской статье. В-третьих, по вашей же ссылке, если бы вы внимательно посмотрели чуть дальше, цитирую: Для внутренних планет численные расчеты дают хаотичность их положения на орбите. Кроме того, особой проблемой является Меркурий, который... И снова, эта информация опять же присутствует в уже упомянутой выше статье.
В общем, не стоит доверять некачественным источникам. Там есть много особенностей и деталей, но сути это не меняет, хаотическая динамика имеет место быть.
belch84
Ровно то же самое написано и в русской Википедии
Вообще, обвинения Википедии в неточностях стали теперь общим местом, они, на мой взляд, абсолютно незаслужены, сама Википедия (даже и русская) как источник намного более точная, чем некоторые научные работы.В случае Солнечной системы существование хаотческих траекторий вовсе не означает, что планеты реально движутся по именно таким траекториям, поскольку современная точность измерения их положения в пространстве не позволяет однозначно определить их дальнейшую траекторию на миллиарды лет вперед. Теория КАМ говорит, что вероятность того, что конкретная планета через много лет будет двигаться по хаотической траектории, практически нулевая. Следует различать утверждения «для планеты существуют возможные хаотические траектории» и «хаотичность траекторий всех планет теперь является доказанной»
Smog1on1the1water
Я привел вам конкретный пример неточности и некорректности, какие еще могут быть вопросы? Почитайте оригинальную статью, а не пересказ.
Означает. Во-первых, речь идет лишь о планетах-гигантах, в то время как внутренние планеты и система Плутон-Харон отчетливо демонстрируют хаотическое поведение. Реально, и об этом говорится в статье, на которую ссылается русская Вики, почитайте. Во-вторых, даже в случае планет-гигантов речь идет о другом. Если бы вы почитали оригинальную статью, то обратили бы внимание на то, что в ней рассматривается ограниченное число сценариев и лишь на масштабах 200млн - 1млрд лет. При этом, если на масштабах 200млн среди рассмотренных сценариев хаотических было 70%, то на масштабе 1млрд лет - уже 90%.
КАМ этого не говорит, потому что применительно к ньютоновской гравитации корректна лишь для задачи трех тел (и снова в русской Вики об этом забыли написать). Существуют попытки обобщить выводы на задачу n-тел, но они также сталкиваются с теми или иными ограничениями. Применительно конкретно к Солнечной системе проблемой КАМ является существование резонансов, которые разрушают инвариантные торы (и снова в русской Вики тишина про это). Теме резонансов, например, посвящена одна из последних статей уже упомянутого выше Laskar: The origin of chaos in the Solar System through computer algebra.
Как я уже говорил, в этом вопросе много тонкостей, а вы зачем-то прицепились лишь к поведению планет-гигантов. Еще раз повторю - в математическом смысле Солнечная система является хаотической. Вопросы могут возникать лишь в отношении того, насколько.
belch84
Smog1on1the1water
Это даже не я лично, а многочисленное научное сообщество.
Вам не нужно понимать, просто примите к сведению. Земля - круглая. Солнечная система - хаотическая.
А перемешивание это откуда вообще берется? Из нелинейности. Это именно наш случай, тут даже проверять нечего.
belch84
Неплохо было бы, чтобы вы сделали хотя бы одну публикацию здесь, тогда каждый сможет оценить, стоит ли слепо доверять всем вашим утверждениям
Smog1on1the1water
Напишите это всем тем авторам, ссылки на которых я вам тут давал, они будут очень рады.
Мои, к примеру, есть в Physica D: Nonlinear Phenomena, потому что динамический хаос в нелинейных системах является частью моей специализации как теоретика. Так что я от чистого сердца пытался донести до вас положение дел, а вы зачем-то в бутылку полезли. Неприятно.
belch84
Smog1on1the1water
Смотрите, какая тут история.
1. Вы сделали утверждение, что система гравитационно-связанных тел хаотической не является. И сослались на КАМ. Но, во-первых, КАМ тут не работает, я уже объяснил почему. Во-вторых, я сослался на Жака Ласкара, который в работе 1989 года показал, что Солнечная система демонстрирует хаотическое, а не квазипериодическое поведение. Вот, можно перейти по этой ссылке, если не верите мне. Там вот прямо черным по белому так и написано, и повторяется в каждой научной статье.
2. Вы ткнули меня ссылкой на Вики про планеты-гиганты. Но, во-первых, в первую очередь всегда говорят про внутренние планеты и Плутон-Харон, поскольку для них время Ляпунова относительно мало (от 1млн до 30млн лет, что более-менее в рамках человеческих интересов). И здесь никаких сомнений нет вовсе. Во-вторых, поведение планет-гигантов - это отдельная тема. И даже если их поведение относительно "регулярно", это не влияет на основную часть вопроса - таки хаос в Солнечной системе есть безотносительно типа их собственного поведения. Поэтому ваше исходное утверждение в любом случае ложно, так как в принципе отрицает возможность хаоса.
3. Но вернемся к планетам-гигантам и известной статье, на которую ссылается русская Вики. Внимательно ее прочтем, про что она? В ней говорится, что существует противоречие между различными работами, где в одних случаях демонстрируется хаотическое поведение планет-гигантов, а в других - нет. С чем это противоречие может быть связано, и как его разрешить? В статье приходят к выводу, что противоречие не связано с вычислительными ошибками, оно объективно. А причина кроется в начальных условиях задач интегрирования, а именно в неточности текущих наблюдательных данных, в результате чего время Ляпунова для планет-гигантов может меняться в широких пределах, буквально от миллионов до миллиардов лет. По этой причине в одних работах удалось наблюдать хаос, а в других - нет (не хватало модельного времени). И если среди ансамбля траекторий в статье на отрезке 200млн лет было лишь 70% решений с хаосом, то на отрезке в 1млрд лет - уже 90%. Это не отрицание хаоса, а указание на то, что время Ляпунова может быть весьма значительным.
Обратите внимание - моего личного мнения тут нет ни на одном из этапов, мы говорим лишь о мнении научного сообщества.
belch84
Пожалуйста, можете указать, как это соотносится с вашим безапелляционным утверждением?
Перешел по ссылке, обнаружил статью о француском астрономе, постровшем одну из моделей Солнечной системы, которая для некоторых из планет на периодах в сотни милионов лет предсказывает хаотическое поведение. Точно не буду углубляться в исследования его модели, понимаю только, что значения достаточно многих её параметров можно обсуждать (например, не знаю, как они там определяют массы планет, подозреваю, что ошибки там могут быть значительными). Особенно понравилась фраза из статьи по ссылке Понятно, что слегка хаотических сценариев там может быть больше, но несомненно хаотических — 1% (как там насчет меры нуль?).
Вообще, ваши комментарии к статье об относительно простой симуляции Солнечной системы вызывают ощущение, что вам хочется, так сказать, «блеснуть эрудицией», расссказывая о моделях, работающих на диапазонах в сотни миллионов лет. Для моделей, подобных той, которая описывается в публикации, обсуждать хаос смысла нет
Smog1on1the1water
https://habr.com/ru/articles/755724/comments/#comment_25877160
Ага, а Эйнштейн, стало быть, работник патентного бюро.
Слушайте, ну это уже просто напросто невежливо. Вы реально начали вести себя уже как плоскоземельщик. Ну зачем вот это вот все? Только ради того, чтобы до последнего бороться за неправильное, но все-таки свое мнение? Блин, ну это смешно.
А вы не обратили внимания, что не привели ни одного возражения по существу, и при этом давно уже перешли на личности, причем не только в мой адрес, но и научного сообщества вообще? "Подозреваю, понравилось, не буду углубляться..." Это, конечно, весьма научные аргументы. А вы возьмите и углубитесь! Ну видно же невооруженным глазом, что плаваете в теме. Вот эти вот попытки сослаться на КАМ, неудачные отсылки к википедии, слова про "меры ноль" - это все настолько нелепо и грустно. Нет хаоса в Солнечной системе? Прекрасно! Жду вашей публикции в Phys. Rev. в ближайшие дни!
А это так и вообще просто позор какой-то. Вы не читаете дальше одного абзаца и не понимаете смысла написанного, лепите одно с другим без разбору.
В начале абзаца по сути написано, что работы Ласкара 1989 и 1990 года стали общепризнанными. А дальше, где вы процитировали, речь про совершенно другую работу 2009 года на основе ППН формализма, дабы исследовать вклад неньютоновских и других поправок в общую нелинейность системы. Это вообще не про количество хаотических сценариев в принципе. Ваша очередная попытка аргументации разбита просто напросто вдребезги, потому что вообще мимо и не в тему.
Вы невнимательны. Хаос я и не обсуждал. Это вы зачем-то начали неправильно поправлять Pavgran, что и заставило меня вступить в вашу с ним дискуссию о хаосе. Все остальные мои замечания к публикации касаются лишь качества счета и ответов на прямо заданные вопросы. Вы зачем-то снова все перепутали.
belch84
Скажите пожалуйста, если я сформулирую поправку к публикации уважаемого Pavgranа примерно так — да, хаотическое поведение для планет Солнечной системы действительно возможно, но заметить его будет чрезвычайно трудно, заметно проявляется оно только на периодах в сотни миллионов лет и пока удалось его подтвердить только для внутренних планет, не для всей Солнечной системы, для которой некоторые исследования подтверждают хаотичность, а некоторые нет — такая поправка не будет оскорблять уважаемого Pavgranа, а также персонально вас и все научное сообщество в вашем лице?
Ну и еще про дребезги
О каких количествах тогда речь здесь?
И, пожалуйста, очень прошу вас — не волнуйтесь, то, что кажется вам переходом на личности — это просто реакция на ваш менторский тон Я ведь сам могу решать, что мне нужно понимать, а что нет, верно?
Smog1on1the1water
А как вы думаете, плоскоземельщики не тем же самым образом рассуждают?
О числе катастрофических сценариев. Хаотический и катастрофический - не одно и то же, хаотических там все 2501 случай.
Нет, это называется заметанием сора под ковер. Точно так же можно было бы говорить - ну все-таки в рамках человеческого роста и даже инфраструктуры городов Земля является плоской, а вот так называемая якобы сферичность - ну она возможна, но заметить ее было бы очень трудно, да и вообще не особо кому-либо удалось подтвердить.
Общим научным консенсусом является присутствие хаотического поведения в динамике планет. Без всяких отговорок. Откройте любую работу - она начнется именно с этого. Можно, к примеру, того же Батыгина: Advances in computational technology and space travel have sparked continued interest in the problem of planetary orbits. In particular, it has been demonstrated that the solar system displays chaotic behavior on sufficiently long timescales (Laskar 1989, 1990; Sussman & Wisdom 1992). The four terrestrial planets display chaotic motion with a Lyapunov time on the order of 5 million years, as do the Jovian planets (Laskar 1989; Murray & Holman 1999 and the references therein). Furthermore, the mass ratios of the planets to the Sun are much larger than those required by the KAM theory to assure strictly bounded, quasi periodic variations of the orbital elements (Arnold 1961). It therefore appears that the solar system may ultimately be dynamically unstable.
Видите, что является дискуссионным вопросом? Не наличие/присутствие хаоса, а возможность катастрофических сценариев с потерей глобальной устойчивости. Вот что является предметом исследований, отсюда и свежая статья Жака Ласкара про резонансы, ссылку на которую я уже приводил, и интерес к релятивистским поправкам и пр. эффектам, влияющим на степень нелинейности в системе.
Ну и обратите внимание - всего один абзац из работы Батыгина затрагивает сразу ВСЕ вопросы, которых мы касались. Это всё, чего данная дискуссия реально стОит, вы совершенно зря упорствуете.
Smog1on1the1water
Даже у вас на картинке симуляции движения планет земного типа видно, что орбиты спиральные, второй оборот не совпадает по радиусу с первым. Проблема не в том, что расхождение небольшое, а в том, что оно накапливается постоянно. В методе Эйлера нигде нет коррекции этого расхождения, посмотрите еще раз картинку из Вики, ссылку на которую я дал. В результате, чем больше итераций, тем больше расхождение. Даже если вы сделаете шаг интегрирования очень и очень маленьким, итераций станет настолько же больше, и просто спираль будет получаться более гладкой. Отсутствие коррекции в самом методе интегрирования (замены дифференциалов на конечные разности и приращения) - неустранимый недостаток метода Эйлера. В методах математической физики есть отдельный раздел, который связан с вязками и невязками разностных схем. Их можно придумывать и так, и эдак, но в данном случае вполне достаточно пользоваться общепринятыми и общеизвестными методами, изобретать велосипед тут не нужно. Нужно просто взять более точный метод, чем метод Эйлера. Для начала. А если вы захотите моделировать еще и столкновения или максимально близкие сближения тел, то тут и без переменного шага интегрирования не обойдется с методом контроля и коррекции.
Не могу сказать за все ВУЗы, но у нас на физфаке во времена моей юности эту задачу разбирали на первом курсе. И я своими глазами насмотрелся на все веселые ньюансы, которые тут возникают на разных этапах сложности решения.
oburdelev
Интересовался ранее этой темой но далее метода Эйлера не ушел. Подскажите пожалуйста, какие более точные методы использовать для численного моделирования задач 2 и 3 тел? Будет здорово, если покажете направление, где можно почитать.
Pavgran
Ну, для самого начала можно почитать про семейство методов Рунге-Кутты, например. Они достаточно просты в реализации и большинство из них имеет больший порядок точности, чем метод Эйлера. Дальше можно начать изучать методы интегрирования, сохраняющие энергию системы. Я сам эту тему не изучал, но в гугле по запросу "energy-preserving integration for n body problem" нашлось несколько интересно выглядящих результатов.
Milliard
Для простых орбит подойдет метод Рунге-Кутты, как ответили выше. Если нужна высокая точность с тесными сближениями тел, то метод Адамса-Башфорта. Есть реализации метода (решатель ode113) на многих языках.
Smog1on1the1water
Если вам прям интересно-интересно, то вот одна из известных и цитируемых работ на эту тему (надеюсь, токен не сдохнет): A hybrid symplectic integrator that permits close encounters between massive bodies, J. E. Chambers, 1999. Там во введении есть обзор и более ранних методов. Указанные методы делают акцент именно на том, чтобы ошибка сохранения энергии на масштабах миллиардов лет была минимальна. Ну а более простые методы уже указали.
vk6677
Эдвард Лоренс из-за ошибок округления при распечатке результатов и их повторного ввода в компьютер даже стал пионером в разработке теории хаоса.
При таком масштабе расчетов ошибка будет очень быстро накапливаться.
Deosis
Раз уж у вас есть симуляция, то можно просто запустить и посмотреть, что произойдет на масштабах в тысячи лет.
unclegluk
Году в 90-м, будучи школьником, нечто подобное ваял на Фокале на ДВК2. Здесь даже подход комментировать не стоит. Задача на красивую картинку для привлечения одноклассниц и пятерку по астрономии.