
Одна из страниц его биографии известна чуть менее широко. Связана она с решением поистине чудовищно сложного для тех времен алгебраического уравнения 45-ой степени!
В 1594 году Виет прославился как математик на всю Европу. Известный голландский математик того времени Адриан ван Роумен предложил математикам Европы решить составленное им уравнение 45-й степени и разослал письменный вызов в разные страны. Во Францию он письмо не отправил, так как считал, что там нет математика, способного решить поставленную задачу.
Само уравнение имело вид:

В современной записи оно выглядит следующим образом:
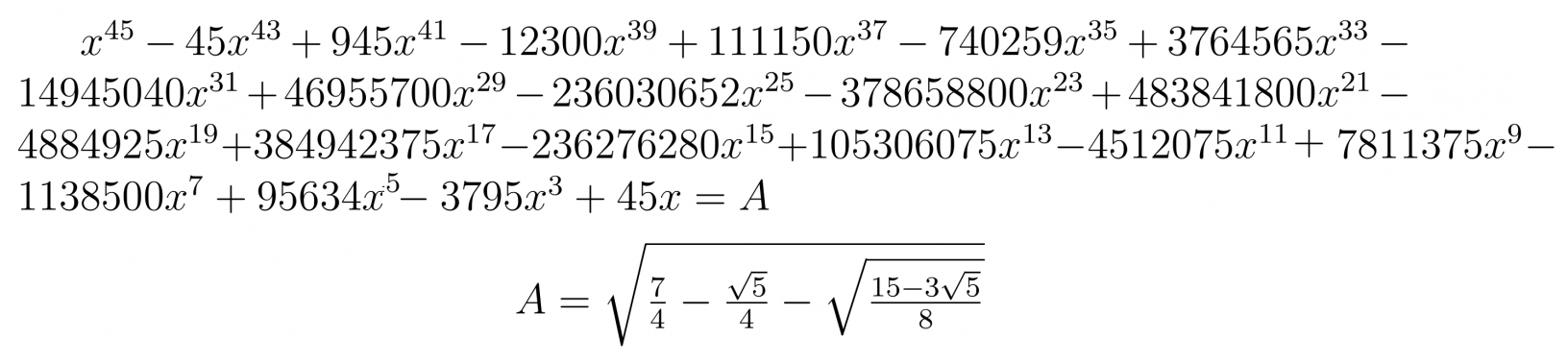
Каждый из коэффициентов велик, и ни один из них не является простым. Девятнадцать из них, например, делятся на 5. 95 634 делится на 7. 236 030 652 делится на 12. 740 259 делится на 3. Кроме того, коэффициенты постепенно увеличиваются к середине. Эту закономерность демонстрируют такие биномы, как (x + y)^n.
Большинство источников не уточняют, каким именно образом ван Роумен придумал это уравнение, ведь, согласитесь, из головы такое взять невозможно. Ответ на этот вопрос мы узнаем, когда прочитаем, чем был известен голландец.

Ван Роумен был профессором математики и медицины с 1586 по 1592 год, а затем в течение шести месяцев в 1592 году был ректором Лёвенского католического университета. За это время он спланировал опубликовать обзор всей математики:
В качестве первой части этого проекта он работал над «theoria polygonorum», теорией правильных многоугольников. Результатом этого должны были стать таблицы синусов, касательных и секущих, а также решение задачи о возведении окружности в квадрат, что для него означало вычисление пропорции между длиной окружности и диаметром окружности. Предполагалось, что работа будет состоять из 12 глав, в первых четырех из которых будут рассмотрены правильные 3-, 4-, 5- и 15-угольники и связанные с ними многоугольники, полученные многократным удвоением числа сторон. В разделах 5-9 рассматриваются все остальные правильные многоугольники. В главах 10 и 11 ван Румен изучал круг. В 10 разделе будет рассказано, как вычислить его окружность и площадь. В 11 разделе будут рассмотрены многие ошибочные или просто неправильные решения проблемы возведения круга в квадрат. Наконец, в разделе 12 будет показано, как необходимые арифметические операции могут быть выполнены с наименьшими трудностями.
Оказывается, традицией того времени было завуалированно сообщать о своих открытиях. Именно эту цель и преследовал ван Роумен. Получив новую общую формулу для составления таблиц тригонометрических функций, он просто свёл к уравнению одно из вычисленных им значений.
В защиту этой позиции есть неопровержимый факт. Ван Роумен привёл в письме несколько решений уравнения при других значениях правой части, например:
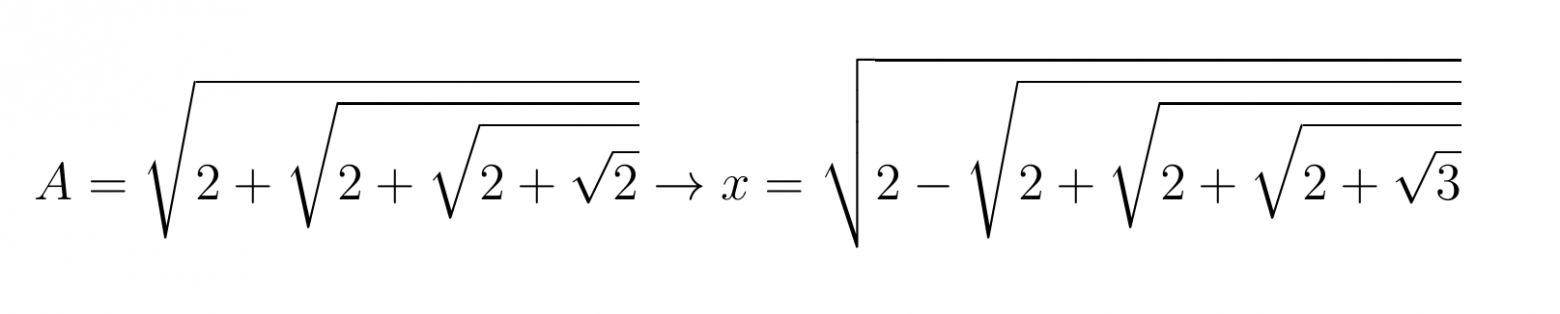
Уравнение ван Роумена было упомянуто на встрече голландского посла с королем Франции Генрихом IV. Посол Нидерландов тогда отметил, что «ни один французский математик не был включен в составленный ван Роуменом обзор великих математиков». Возмущенный монарх ответил, «что их есть у нас» и поручил передать задачу Виету. Посмотрим же, как Франсуа мог расколоть этот «крепкий орешек».
❯ Левая часть уравнения
Гениальность француза, решившего это уравнение практически сразу, заключалась в том, что он вывел формулу, по которой в левой части получаются коэффициенты при х. Используя современные обозначения:

Некоторые источники говорят, что этот алгебраический вывод — следствие величайшей геометрической интуиции Виета, связавшего уравнение с построением правильных вписанных многоугольников.
Оценив количество множителей в левой части уравнении Виет определил, что n=45… Если хочется убедиться в справедливости формулы, то пожалуйста:
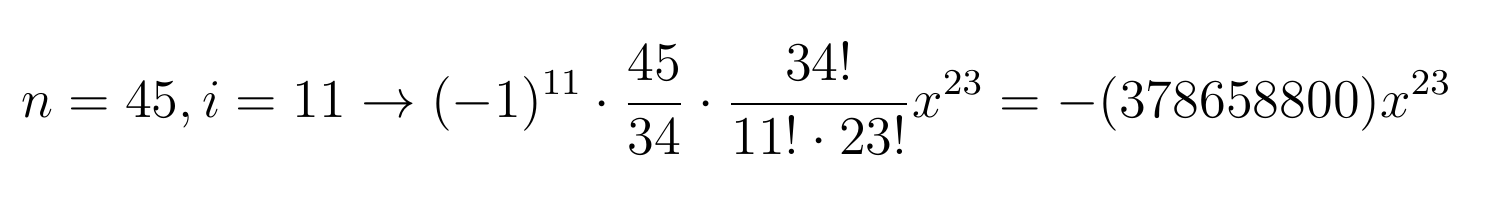
Все остальные коэффициенты получаются аналогичным образом.
❯ Правая часть уравнения
Зацепившись за примеры решения уравнения, которые были представлены ван Роуменом в письме, Виет «почуял» тригонометрию. Выкладки были примерно такие:

Врубив рекурсию на максимум, Виет смог показать, что значение А, которое было приведено выше, не что иное, как:
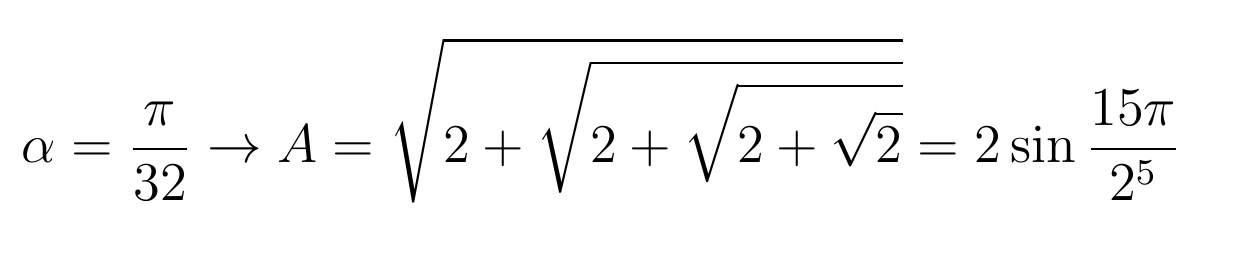
Оставив любопытному читателю все остальные преобразования, покажу, чего добился Виет со значением А из исходного уравнения:

Теперь вернемся к общей формуле, вычисляющей коэффициенты разложения. В первом множителе там число 45, втрое большее знаменателя выше, что наводит на общую формулу:

Вместо х, как в исходном уравнении, подставлен удвоенный синус. Приравнивая, получим:
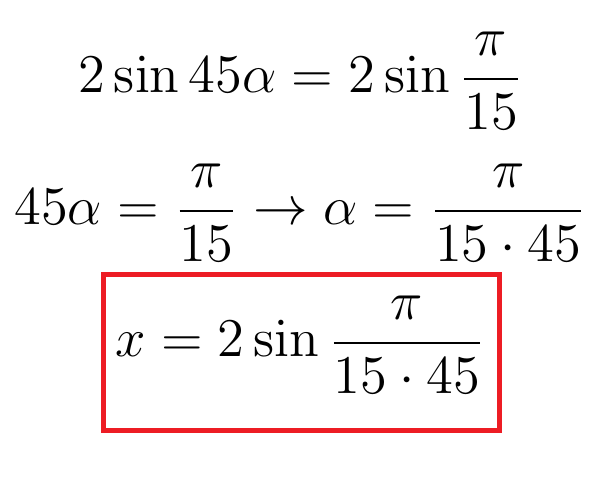
Но синус — функция периодическая, и у этого уравнения Виет нашел еще 44 решения, все из них вида:
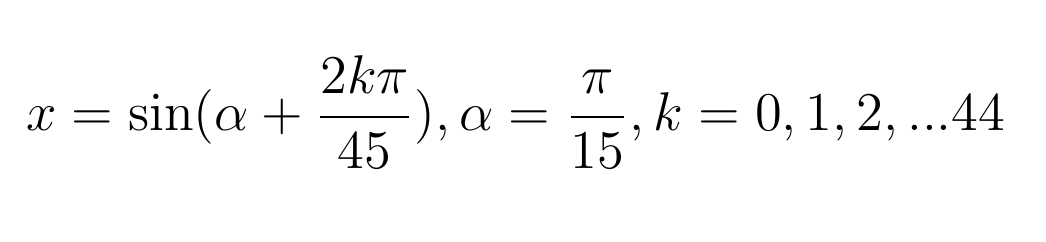
Франсуа, впрочем, признал только 22 положительных решениях, потому что отрицательные вовсе не считал нужным показывать. Если учесть, что алгебраическая символика еще была несовершенной, не было обозначений тригонометрических функций, не было удобного обозначения радикалов, то решение Виетом уравнения ван Роумена действительно вызывает восхищение. Как результат, Виет прославился на всю Европу и значительно повысил авторитет французских математиков.
- Больше математики в Telegram — "Математика не для всех".
Возможно, захочется почитать и это:
- ➤ «Он должен быть стать вторым Ньютоном» — говорил Харди о Рамануджане после первого письма. Что же такого написал индиец?
- ➤ Big data. Математика на службе биологии
- ➤ 96 лет со дня рождения Джона Маккарти
- ➤ Инопланетная математика
- ➤ Как создавали Sid Meier's Civilization

Комментарии (54)

wataru
11.09.2023 13:09+86Когда увидел "функцию пола" слегка офигел. Это весьма странный дословный перевод функции floor. По-русски обычно говорят "функция округления вниз".

andreybrylb Автор
11.09.2023 13:09+9На самом деле достаточно удобно: есть функция пола и функция потолка)

wataru
11.09.2023 13:09+27Если бы оно было общепринятым, то - да. Тогда было бы короче писать. А так вам пришлось там же еще и расказывать, что эта функция "пола" делает. Просто "округление вниз" было бы в итоге короче.

grey_narn
11.09.2023 13:09+7В (очень профессиональном) переводе "Конкретной математики" именно пол и потолок, вроде бы.

aamonster
11.09.2023 13:09+3Программисты их обычно называют по-английски, а у остальных короткого названия нет)

Old_paranoid
11.09.2023 13:09А также замечательная обобщенная функция 4S+2P (4 стены, пол, потолок) другими словами, "от фонаря" :)

youngmysteriouslight
11.09.2023 13:09-8Ух ты, поражен до глубины. Я пропустил первые абзацы и бегло прочитал остальное. Подумал, что «функция пола» так называется из-за специфики предметной области — тогдашних гендерных исследований. Мол, мальчик-девочка-мальчик-девочка-… — вот вам n%2 = n - 2 * floor(n/2) для определения пола (правда, почему-то написано только floor(n/2), но да бог с ним, подумал я). Всё оказалось гораздо прозаичнее.

mayorovp
11.09.2023 13:09+1В переводах "Конкретной математики" и "Искусства программирования" используются именно "пол" и "потолок".

vasily-v-ryabov
11.09.2023 13:09+11Функция пола - тоже царапнуло, но там ещё и слово «целое» пропущено. :) Должно быть «ближайшее целое число», а не просто «ближайшее число».

D7ILeucoH
11.09.2023 13:09Ближайшего числа не существует) это аксиома непрерывности действительного множества чисел. Так что вполне адекватно используется подразумевание целых чисел

Lodary
11.09.2023 13:09В "Конкретной математике" Кнута тоже переводили как пол и потолок. Округление вниз/вверх общепринято, но пол/потолок довольно мило все-таки :)

Zenitchik
11.09.2023 13:09Пока я не начал изучать английский, мне даже в голову не приходило, что floor - это слово, а не просто имя функции. ))))

janatem
11.09.2023 13:09В исходном уравнении, по-видимому, опечатка: третий с конца моном 95634x на самом деле должен быть кубическим.

janatem
11.09.2023 13:09+30Авторам статей напоминаю, что в редакторе Хабра поддерживается нормальный LaTeX. Вставлять заранее отрендеренные картинки некрасиво — они масштабируются произвольным образом, так что короткие формулы кажутся набранными гигантским шрифтом. Давайте не будем уподобляться medium.com, там математические статьи выглядят реально по-уродски. (Мне доводилось там не только читать, но и писать, это больно.)

wataru
11.09.2023 13:09Важное замечание: В новом редакторе хабра. Для редактирования статьи надо переключиться на новую версию (кстати, кто еще не в курсе, там вроде как запилили трекер! Можно переключатся).

janatem
11.09.2023 13:09+1И в старом было, всегда его использовал. Сломали разве?

wataru
11.09.2023 13:09Когда-то давно - не было в старом. А потом я стал статьи в новом писать. Не в курсе про формулы в старом редакторе. Может и есть, но вряд ли так удобно - что формулу показывает сразу как вы ее пишите.

MaFrance351
11.09.2023 13:09Это статья из корпоративного блога. Конкретно тут есть требования писать именно в старом редакторе.

NooneAtAll3
11.09.2023 13:09а как переключаться?
я помню попытался попробовать что пописать, но посмотреть на старый редактор вообще не смог

Zenitchik
11.09.2023 13:09В самом низу страницы есть ссылка "Перейти на новую версию" https://habr.com/berserk-mode-yarr

NooneAtAll3
11.09.2023 13:09это в смысле что выбирать редакторы можно только на новохабре?

wataru
11.09.2023 13:09+1Вы не можете выбирать редакторы отдельно. Хотите новый редактор — переключайте весь хабр на новую версию.

vladf
11.09.2023 13:09+8Вот эта часть заставила вспомнить высказывания "очевидно, что" из учебников, над которыми думаешь часами... Так и не понял как сделан данный переход:
"Теперь вернемся к общей формуле, вычисляющей коэффициенты разложения. В первом множителе там число 45, втрое большее знаменателя выше, что наводит на общую формулу"

Refridgerator
11.09.2023 13:09+3Функцию пола автор перевёл, а упоминать про биномиальные коэффициенты, в которых и вся соль, почему-то не стал.

mayorovp
11.09.2023 13:09+13Результатом этого должны были стать таблицы синусов, касательных и секущих, а также решение задачи о возведении окружности в квадрат, что для него означало вычисление пропорции между длиной окружности и диаметром окружности.
Это так квадратуру круга перевели?

domix32
11.09.2023 13:09+4функция пола, которая возвращает ближайшее меньшее к аргументу число
по-русски оно обычно называется округление вниз и возвращает ближайшее ЦЕЛОЕ меньшее либо равное заданному аргументу.



dave2
Иногда мне кажется, что Хабр это окно в параллельную вселенную.
ssj100
с 6 класса - теорема Виета
avost
Речь, видимо о том, что кто ж её любил? Как только узнавали про метод с дискриминантом, так и забывали о Виетте с облегчением :).
По крайней мере в моей вселенной было так.
Ребёнки мои сейчас тоже так считают.
Но вселенная, где эту теорему любят наверняка существует, раз о ней написано на хабре :)
Alexandroppolus
Нам в школе сначала рассказали про дискриминант, а позже про теорему Виета. Я обычно сначала пытался по-быстрому "смекнуть" решение с помощью неё, и только если не удавалось, расчехлял более трудоемкий, но безотказный дискриминант.
Эпизод с 45 степенью тоже смутно припоминаю, вроде об этом было пару слов в учебнике.
MaFrance351
Я ей пользовался. Видимо, мне везло, так как довольно часто получалось достаточно быстро найти.
Zenitchik
Я в детстве её любил. С ней для школьных примеров часто удаётся быстро угадать ответ, что избавляет от писанины.
Кстати, проходили мы её позже, чем дискриминант. Сильно позже.
qw1
AlexMih
Формально говоря, Виета про другое - если известны корни x1 и x2, то по ней можно быстро состряпать подходящее уравнение. Графически говоря, по двум точкам подобрать параболу. Но не сказал бы, что это частая задача.
А вот как именно находить по ней корни - никогда не понимал, несмотря на все свои олимпиады и медали. Перебирать x1, хотя бы от 10 до -10, вычислять по одной формуле x2 и проверять подстановкой в другую формулу? Так дискриминантом быстрее.
mayorovp
Именно что перебирать. Только не "от и до", а по целочисленным делителям. Разумеется, так можно решить только "школьное" уравнение, где специально закладывались "красивые" корни.
lorc
Ну не обязательно прямо подбирать. Просто смотрим на q. Если оно, грубо говоря, из таблицы умножения, то имеет смысл разложить его на делители. Например если мы видим уравнение x^2 - 8x + 12 = 0 то очевидно что 12 можно разложить либо 3*4 либо 2*6. Соответственно, имеет смысл проверить корни 3 и 4, а также 2 и 6. В данном случае подходят корни 2 и 6, ибо 2+6 = 8.
Scott_Leopold
Зачем перебирать? Это же просто система из двух очень простых уравнений (если коэффициенты p и q известны).
qw1
Которая, при решении "в лоб", сводится к уравнению 2-й степени. Бадум-с!
Ergistael
А вот когда нам рассказали о Теореме Безу (правда, без доказательства, но разрешали пользоваться)...
Scott_Leopold
Так происходит, потому что обычно в школе не объясняют теорему Виета как следует.
На самом деле, она действительно проста и изящна. Куда больше, чем дискриминант.
uszer
Реально некропост про какую-то альтернативную версию школы. "Все любили... ". Не надо за "всю Одессу" говорить, да и Одесса уже "не та"...
oleg_rico
Вероятнее всего автор учился в школе с математическим уклоном где и бином Ньютона в старших классах проходили. В обычных школах всё заканчивалось на решение квадратичных уравнений.
sergku1213
У Вас что была особая школа ?. Десятый класс школы - первообразная, скомканное изучение дифуров и интегралов. Ну как сказать, изучение...в основном понятие. Просто большинство прошли мимо