На 12м году опыта программирования микроконтроллеров мне наконец-то пригодилась школьная тригонометрия. Это настолько специфический случай, что я решил написать про это заметку.
Когда Вам надо добавить в устройство звук, то можно воспользоваться микросхемой MAX98357A. Чип этого же семейства MAX98357B можно встретить вообще в Apple AirTag!
Это по сути DAC у которого на входе I2S, а на выходе PWM 330kHz. Меняется только скважность PWM сигнала в зависимости от значений PCM отсчетов в канале I2S.

Главный плюс таких D усилителей - это высокий КПД и высокая энергоэффективность.
В семействе MAX98357x только 2 чипа: MAX98357A, MAX98357B. Вот что значит расшифровка PartName.

Далее я буду работать с MAX98357A.
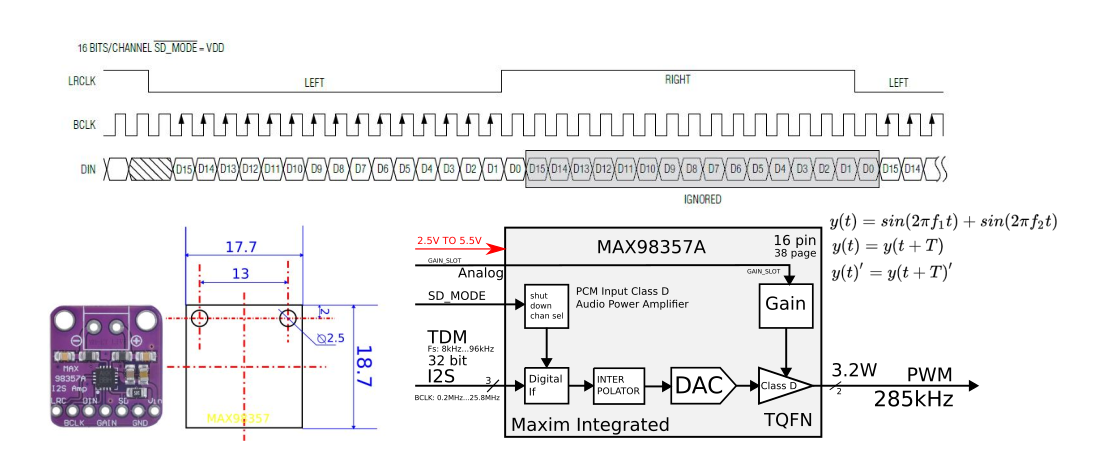
С точки зрения программиста микроконтроллеров чип выглядит так. Тут можно заметить приемник I2S, цифро-аналоговый преобразователь DAC, усилитель D-класса (по сути генератор PWM), регулятор громкости напряжением. Еще в спеке сказано, что внутри присутствует осциллятор на 330kHz.

Распиновка микросхемы MAX98357A

ASIC примечателен тем, что для него есть специальная отладочная плата. На корпусе микросхемы написано AKK 7AA.
Распиновка PCB отладочной платы

Габариты отладочной платы показаны на рисунке ниже, это 17.7x18.7 мм. Вот чертеж.

Так как чип получает данные по I2S, то приведу подсказку по интерфейсу I2S. I2S это 4х проводной двухканальный синхронный полнодуплексный последовательный интерфейс передачи цифровых данных. Топология соединения Master-Slave. Битовая скорость до 3MBit/s. Интерфейс передает отсчеты DAC/ADC в формате big-endian знаковых чисел в кодировке two's complement integer (PCM). Вот пожалуй всё, что надо знать про I2S в 90% случаев.

В теории так выглядит осциллограмма передачи звука.

А вот так выглядит осциллограмма работающего звука 1kHz на практике. Тут видны PCM семплы со значениями 32, 1, -31, 63. Заполнены оба канала. Звук есть.
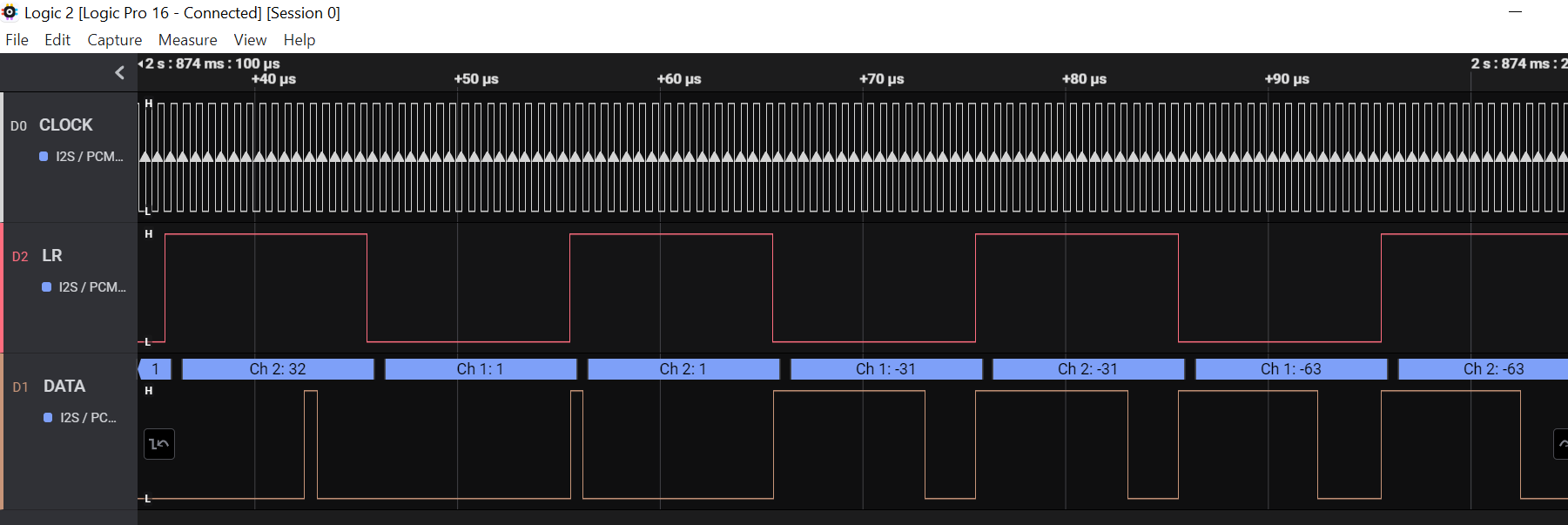
А вот если передавать PCM данные только по правому каналу то звука не будет. Это потому, что у меня сейчас на проводе SD_MODE напряжение 3,3V.
В чипе MAX98357x выбор канала задается напряжением на пине 4 SD_MODE. Обычно это делается установкой резисторов подтяжки напряжения. Таким образом проводом SD_MODE можно включать или отключать звук даже, если в шине I2S бежит трафик.

Если передавать данные только по левому каналу, то звук снова есть. Это и ожидаемо, ведь на проводе SD_MODE 3.3V.
Очевидно, что сейчас чип MAX98357A выхватывает PCM отсчёты только из левого канала I2S.
А это сигнал на выходе усилка. Тут PWM на частоте 285714 Hz, хотя в спеке заявлено 330 kHz.

Вообще сигнал с усилителя D-класса следует пропускать через фильтр нижних частот. Однако электромагнитные звуко излучатели сами являются в том числе и ФНЧ. В качестве звуко излучателя я взял спикер от колонки JBL Clip3.

Вот такой получился прототип. Пришлось соединить все компоненты общей пластмаcской из оргстекла.

Отладка
Как же убедиться, что звуко-излучатель работает на той частоте, которую в самом деле установили?
Вариант №1: Воспроизвести синус.
Надо воспроизвести тестовый звук. Что-нибудь предельно простое, например синус функцию. Затем измерять частоту и сравнить измеренную частоту с воспроизведенной частотой. Если значения совпали, то значит акустическая система воспроизведения работает четко.

Вот таблица предварительно рассчитанных в RAM памяти микроконтроллера PCM семплов

Теперь, когда звук присутствует, можно воспользоваться мобильным приложением Audizr. Это акустический спектро анализатор для мобильных телефонов с OS Andriod. Подразумеваю, что мобильное приложение в real-time вычисляет DFT. Вот на экране мобильного телефона видно, что тон в самом деле 1000 Hz.

Вариант №2: Тестирование звукоизлучателя DTMF интерфейсом
В предыдущем параграфе мы проверили только одну частоту: 1kHz. Однако как проверить остальные частоты? Есть решение.
Можно на микроконтроллере рассчитать двухтональный сигнал и воспроизвести не просто синус, а сумму синусов. То есть DTMF тоны для кнопок 0, 1, 2, 3, ... D, *, #. Затем поднести мобильный телефон с работающим мобильным приложением DTMF Тone Decode и принять цифры. Если в GUI приложения принялись те же числа, что в коде модульного теста, то это значит, что акустическая система полностью исправна.
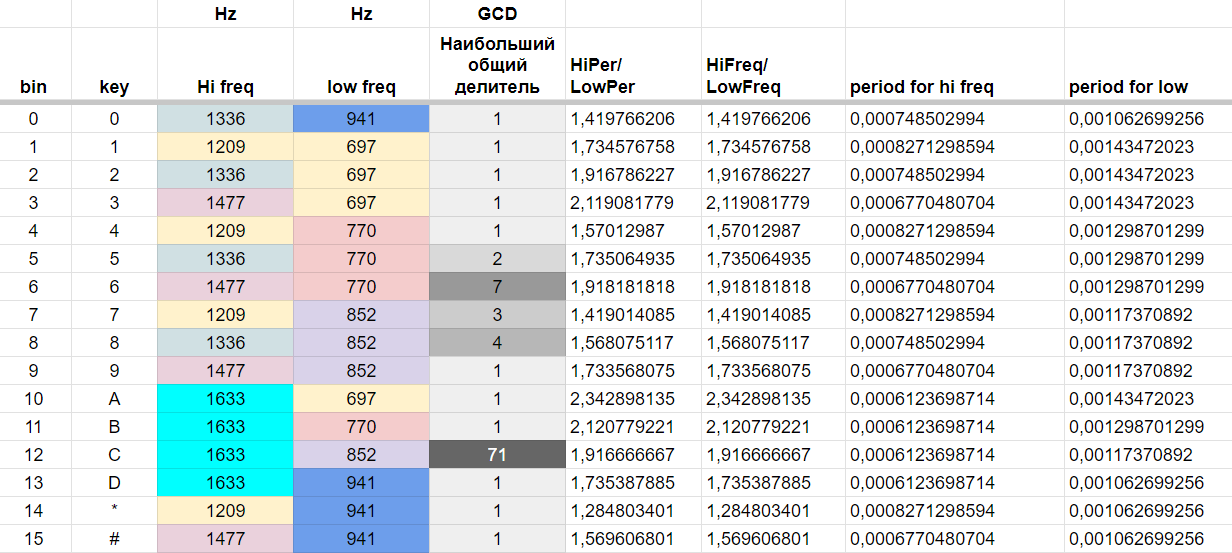
Вот DTMF частоты, которые соответствуют кнопкам

Надо рассчитать звуковую дорожку для каждой кнопки и воспроизвести её. И тут наступает серьезная проблема.
Сколько отсчетов надо расcчитать для каждого тона DTMF?
Очевидно, что никто не собирается подключать SD карту и всю память записывать гигабайтными однообразными тонами DTFM в *.wav файлах. Надо попытаться найти минимальный период для каждого из 16 тонов.
Эту задачу легко формализовать. Надо просто для каждой пары f1, f2 найти Т. То есть 16 раз решить систему уравнений (1) (2) (3).
Надо как-то выразить T через f1, f2.
Решая эту систему уравнений в общем виде, я пришел к выводу, что решения нет. Особенно для таких странных частот как f1=1336, f2=941. Для решения системы уравнений (1-2-3) частоты DTMF это совсем не подарок судьбы. Они даже не в 2 раза отличаются между собой. Сайт Wolfram Alfa даже отказался искать численно решение за бесплатно.
Если решение и есть, то период уходит далеко в века. В микроконтроллере по-любому не хватит никакой памяти, чтобы сохранить дорожку размером в период для суммы синусов с разрешенными частотами. В общем из-за этого у меня было в тот вечер плохое настроение.
Как же быть?
Я решил попробовать найти период DTMF тонов "на глаз". Для этого я написал Python скрипт для, того чтобы самому лично пройтись по звуковой волне.
import matplotlib.pyplot as plt
import math
import numpy as np
f2=770.0
f1=1477.0
Fs=48000
T=0.01
T_fs= 1.0/Fs
t = np.arange(0, T, T_fs)
Y1 = np.sin(t*2*math.pi*f1)
Y2 = np.sin(t*2*math.pi*f2)
Y =Y1+Y2
plt.plot(t, Y)
plt.title('signal')
plt.xlabel('Time,[s]')
plt.ylabel('PCM, ')
plt.grid()
plt.xticks(rotation=-90)
plt.show()Получился вот такой график для тона "5" : 1336 Hz, 770 Hz.
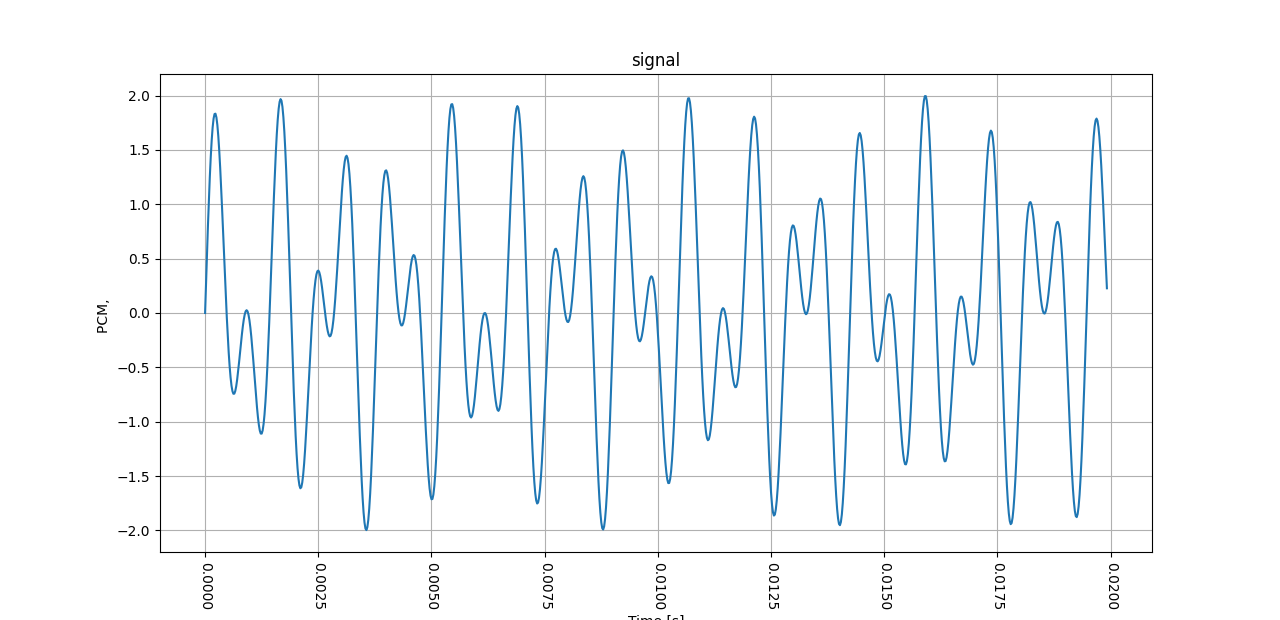
В результате пришлось пойти на нелегальные действия и выбрать так называемый псевдо период. То есть часть графика, которая хоть как-то визуально повторяется. Для тона 5 получилось значение 9021858 ns=9021.858 us=9.021858 ms.

Для остальных тонов я поступил аналогично. В результате у меня кристаллизировалась вот такая LookUp таблица псевдо периодов для DTMF.
static const DtmfKeyPadFreq_t DtmfKeypadFrequencies[] = {
{.code = 0x1, .letter = '1', .freq_small_hz = 697, .freq_big_hz = 1209, .min_period_ns=9968000,},
{.code = 0x0, .letter = '0', .freq_small_hz = 941, .freq_big_hz = 1336, .min_period_ns=7465949,},
{.code = 0x2, .letter = '2', .freq_small_hz = 697, .freq_big_hz = 1336, .min_period_ns=8362420,},
{.code = 0x3, .letter = '3', .freq_small_hz = 697, .freq_big_hz = 1477, .min_period_ns=8739477,},
{.code = 0x4, .letter = '4', .freq_small_hz = 770, .freq_big_hz = 1209, .min_period_ns=9095496,},
{.code = 0x5, .letter = '5', .freq_small_hz = 770, .freq_big_hz = 1336, .min_period_ns=9021858,},
{.code = 0x6, .letter = '6', .freq_small_hz = 770, .freq_big_hz = 1477, .min_period_ns=9345112,},
{.code = 0x7, .letter = '7', .freq_small_hz = 852, .freq_big_hz = 1209, .min_period_ns=8248412,},
{.code = 0x8, .letter = '8', .freq_small_hz = 852, .freq_big_hz = 1336, .min_period_ns=8226680,},
{.code = 0x9, .letter = '9', .freq_small_hz = 852, .freq_big_hz = 1477, .min_period_ns=9446054,},
{.code = 0xA, .letter = 'A', .freq_small_hz = 697, .freq_big_hz = 1633, .min_period_ns=8583695,},
{.code = 0xB, .letter = 'B', .freq_small_hz = 770, .freq_big_hz = 1633, .min_period_ns=9155131,},
{.code = 0xC, .letter = 'C', .freq_small_hz = 852, .freq_big_hz = 1633, .min_period_ns=9255729,},
{.code = 0xD, .letter = 'D', .freq_small_hz = 941, .freq_big_hz = 1633, .min_period_ns=8546970,},
{.code = 0xE, .letter = '*', .freq_small_hz = 941, .freq_big_hz = 1209, .min_period_ns=7441866,},
{.code = 0xF, .letter = '#', .freq_small_hz = 941, .freq_big_hz = 1477, .min_period_ns=7444171,},
};Я собрал сборку, запрограммировал микроконтроллер и начал испускать DTMF тоны. Каково же было мое удивление, когда мобильное Andriod приложение DTMF Тone Decode в точности распознало звуки, синтезированные по этим псевдо периодам!
Всё здорово, однако мобильный телефон это автоматизированный тест, который подразумевает участие человека оператора. Как же сделать тест полностью автономным?
Есть такой чип как MT8870. Это DTMF Decoding модуль. Чип вычисляет алгоритм Гёрцеля для 8 частот DTMF и устанавливает двоичный код на 4х битном GPIO порте.

У него на выходе 4хбитный GPIO. Можно подключить его к GPIO отладочной платы и им же принимать воспроизводимый сигнал. Тогда не будет нужды в мобильном приложении и человеке-операторе.
Вот так при помощи старого интерфейса DTMF можно тестировать аудиоаппаратуру.
Недостатки MAX98357A
1--Усилители D-класса трудно отлаживать. Тут на выходе меняется скважность. Если вы воспроизводите синус, то вы осциллографом не увидите синус на выходе. Вы его только услышите. Надо еще прикрепить специально рассчитанный фильтра нижних частот.
2--Нет возможности варьировать громкость. Только Вкл.\Откл.
Достоинства MAX98357A
1++ Простота
2++ Дешевизна усилителя (110 RUR).
3++ Высокая энергоэффективность
4++ MAX98357A не нужно отдельное высокочастотное мегагерцовое тактирование для работы подобно тому как это было в ASICе MAX9860.
Итоги
Удалось разработать драйвер для MAX98357A. Для этого понадобилось написать MCAL для подсистемы тактирования микроконтроллера, I2S, GPIO. Также пришлось разработать программный компонент DAC для вычисления сигналов различной формы (синусы, косинусы). Прежде всего sin с разной фазой, частотой и амплитудой.
Интерфейс DTMF отлично подходит для тестирования звукоизлучающей аппаратуры.
Как обычно, чтобы написать систему тестирования, пришлось затратить в 3 раза больше усилий, чем на написание самого функционала.
Если Вы знаете как решить в общем виде систему уравнений (1-2-3), то пишите в комментариях.
Словарь
Акроним |
Расшифровка |
I2S |
Inter-IC Sound |
КПД |
коэффициент полезного действия |
DAC |
digital to analog converter |
MCAL |
Microcontroller Abstraction Layer |
DFT |
Discrete Fourier transform |
MSB |
most significant bit |
WS |
Word Select |
ASIC |
Application-specific integrated circuit |
LRCLK |
Left Right Clock |
PCM |
Pulse-code modulation |
IC |
integrated circuit |
BCLK |
Bit Clock |
MAX |
Maxim Intergated |
Links
https://habr.com/ru/companies/vdsina/articles/533492/
https://docs.google.com/spreadsheets/d/1m7vS2bYHUwDMsY2KlE-snnw0ZAD8YeDrgGDN_kSPVAM/edit#gid=1473020946
https://habr.com/ru/companies/skillfactory/articles/554452/
https://habr.com/ru/companies/timeweb/articles/555752/
https://stereo.ru/p/t808p-kak-rabotaet-usilitel-klassa-d-ili-ne-takoy-kak-vse
http://latex.codecogs.com/eqneditor/editor.php
Контрольные вопросы
Как работает усилитель D-класса?
Какой период у DTMF сигнала для символа "1"?
Чем интерфейс I2S отличается от интерфейса TDM?
Как найти период суммы синусов?
Комментарии (26)

tminnigaliev
26.11.2023 01:52+6Отвечаю на вопрос о системе уравнений:
Никто не держит дискретизированные дтмф- последовательности в памяти.
Д в слове дтмф означает 'дуал', т.е. то, что синусов в сигнале два. Микросхема ДТМФ генератора умеет генерировать каждый из синусов в отдельности. Делает она это путем проигрывания записанных сэмплов, расчитывает сэмплы на лету или вообще генерирует их аналоговым способом - сказать сейчас не готов (потому что пишу с телефона).
Так или иначе, система не решается у вас из-за того, что сигналы дискретизированы по времени. Т.е. почти любое обрезание по времени приведёт к потере непрерывности сигнала, а значит к появлению в спектре выходного сигнала мусора - внеполосных сигналов.
Если так хочется решить задачу (и найти период, начиная с которого сигнал похож сам на себя) - посчитайте автокорреляционную функцию и найдите сдвиг, дающий пик автокорреляции. Проблема может быть в том, что чем длиннее вы будете брать запись, на которой будете считать xcorr, тем более подходящие пики автокорреляции будете находить каждый раз. Точного попадания, возможно, не добъетесь никогда (потому что частота дискретизации не кратна частотам всех 8 синусов, которые есть в ДТМФ).
А вообще, вы уже чуть-чуть прикоснулись к ЦОС (DSP) пытаясь решить эту задачу. Добро пожаловать. Тут очень интересно и очень многое неочевидно. Товарищи Смит и Лайонс с нетерпением ждут возможности всё вам рассказать и объяснить (правда русский перевод Смита содержит довольно много ошибок и неточностей перевода, а Лайонса днём с огнём не найти - но pdf-ки в сети есть).

aabzel Автор
26.11.2023 01:52Никто не держит дискретизированные дтмф- последовательности в памяти.
Я их тоже не держу. Рассчитываю в run-time аудиодорожку и отправляю на исполнение.
Потом эту же RAM паvять заполняю расчетами для другого тона и тоже отправляю на исполнение. RAM память пере используется.

An_private
26.11.2023 01:52+1А вообще, вы уже чуть-чуть прикоснулись к ЦОС (DSP)
Задумался, кстати, а какой спектр получится в результате проделанной тс операции - вырезания просчитанного куска на примерно 10 мс и его бесконечного повторения. В голове крутится что-то типа свёртки спектра прямоугольного сигнала частотой 100Гц (то есть sinc) и спектра исходного двухтонального сигнала, так как проделанное чем-то похоже на фазовую модуляцию. Но вот как это аналитически посчитать - ума не приложу. Разве что численно в вольфраме или матлабе считать. Нет идей? :)

Sdima1357
26.11.2023 01:52+7Микроконтроллер в состоянии подсчитывать dtmf на лету, из одной небольшой таблицы синуса. Я делал это на 4- х битном контроллере на 400 килогерц в 95 году. Из каждой частоты вычисляете период с запасом в пару бит . Итого 3 сложения, два сдвига вправо и два LUT на отсчет.
То есть сегодня справится любой современный контроллер.

aabzel Автор
26.11.2023 01:52+1Да. Я тоже рассчитываю дорожки в run-time по формуле сложения синусов.

An_private
26.11.2023 01:52+3Надо воспроизвести тестовый звук. Что-нибудь предельно простое, например синус функцию. Затем измерять частоту и сравнить измеренную частоту с воспроизведенной частотой. Если значения совпали, то значит акустическая система воспроизведения работает четко
Генерируемая частота и её значение зависят только от микроконтроллера, который её генерирует. "Акустическая система воспроизведения" на это никак не влияет.
Вот таблица предварительно рассчитанных в RAM памяти микроконтроллера PCM семплов
А если бы вспомнили школьный курс, то достаточно было бы хранить в 4 раза меньше семплов. Так как достаточно хранить только половину полупериода - вторая половина полупериода точно такая же, а второй полупериод в точности равен первому, только с другим знаком.
Если решение и есть, то период уходит далеко в века
Как уже было справедливо указано - все частоты целые, поэтому период в любом случае не может быть больше 1 сек
В микроконтроллере по-любому не хватит никакой памяти, чтобы сохранить дорожку размером в период для суммы синусов с разрешенными частотами
16 вариантов по 1 сек. При частоте семплирования 32кГц и разрядности 16 (дикий оверкилл, на самом деле) получаем 1МБ. А если вспомнить, что вторая половина каждого записи ровно симметрична первой половине, до 512кБ. Для современных контроллеров вполне терпимо.
Но. В любом случае это решение в лоб и так не делают. А делают синтез по таблице.
То есть имеем одну единственную таблицу для значений синуса от 0 до 90 градусов. Как показывает практика обычно 64 точки более чем достаточно. То есть получаем 256 точек на период.
Для каждой генерируемой частоты имеем аккумулятор, который для каждого следующего выходного семпла увеличивается на величину:
генерируемая частота / частоту дискретизации * количество семплов в таблице
Тогда целая часть этого аккумулятора будет номер семпла в таблице, а дробная - определяет с какой пропорцией надо взять этот и следующий семплы для интерполяции. Синус - функция гладкая, поэтому вполне достаточно линейной интерполяции.
Повторяем для всех частот, которые надо сгенерировать, суммируем полученные значения и выдаём на выход.
Всё, простейший табличный синтез.

An_private
26.11.2023 01:52+1Да, я знаю, что аккумулятор может быть целочисленный и так даже удобнее.
Просто не стал уже вдаваться в детали :)

aabzel Автор
26.11.2023 01:52"Акустическая система воспроизведения" на это никак не влияет.
У звукоизлучателя может быть порвана мембрана.

An_private
26.11.2023 01:52+3От этого генерируемая частота не изменится. Максимум появятся гармоники.

aabzel Автор
26.11.2023 01:52А если бы вспомнили школьный курс, то достаточно было бы хранить в 4 раза меньше семплов. Так как достаточно хранить только половину полупериода - вторая половина полупериода точно такая же, а второй полупериод в точности равен первому, только с другим знаком.
Сложность в том, что мне надо на лету менять еще и sample rate: 8kHz, 16kHz, 32kHz, 41kHz, 50kHz, 48kHz, 98kHz, 128kHz.
Слишком много таблиц получится.
An_private
26.11.2023 01:52+2Если мы говорим о вашем алгоритме "в лоб", то вам нужно считать ровно столько же таблиц. Только если хранить в памяти только участок 0-90 градусов, то требования к памяти можно уменьшить в 4 раза.
Если же говорить об алгоритме синтеза по таблице, то предпросчитанная таблица к частоте дискретизации не привязана никак вообще. От частоты дискретизации зависит только величина инкремента аккумулятора. Поэтому таблица всего одна для любой частоты.

LaoWai2000
26.11.2023 01:52+6Частоты DTMF подобраны так не кратно потому, чтоб не вызывать ложных срабатываний при прохождении тонов через тракт с существенной нелинейностью.
Генератор синуса пишется легко в целых числах, не знаю, как на питоне, на це нормально залазит даже в микрочиповский пик, выдающий пять мипсов без умножителя. Так что уравнения решать смысла никакого нет.

ionicman
26.11.2023 01:52+3Я на ATTINY-85 делал FFT 8bit с целочисленным LUT для sin/cos и она занимала памяти совсем чуток (нужно только до 45 градусов хранить) причём одна и для sin и для cos - все выводится отлично на ходу - вообще никаких проблем.

aabzel Автор
26.11.2023 01:52Синус можно еще вычислять алгоритмом CORDIC
https://ru.wikipedia.org/wiki/CORDIC

Sergey_zx
26.11.2023 01:52+3По моему для ЛЮБОГО числа одновременно работающих генераторов достаточно иметь таблицу синусов (точнее, её четверть) и набор счётчиков с соответствующими периодами.
Суммируем их мгновенные значения и получаем значение для шим. Бонусом, тут можно домножать значения для того что бы частоты были с разными уровнями.
При этом, чем выше частота тактирования счётчиков и ШИМ, тем чище будет звук, ибо именно на этой частоте сойдутся кратности выходных частот.

itsWoland
26.11.2023 01:52+2Если решение и есть, то период уходит далеко в века.
В музыке это называлось «полиритм» т.е. в 1 такте проигрывался один звук 5 раз, а второй 4. То есть как минимум их произведение дает полный цикл

aabzel Автор
26.11.2023 01:52+2Есть такой мем, что самое сложное для понимания инженеров - это нотная грамота.

iShrimp
26.11.2023 01:52+3Это задача по арифметике, а не по теории музыки. Если периоды двух сигналов равны t1 и t2 и отношение t1/t2 рационально, то общий период равен НОК(t1,t2). НОК вычисляется как произведение периодов t1*t2, делённое на их НОД.
Если отношение t1/t2 иррационально, то алгоритм Евклида будет выполняться бесконечно долго. Но можно разложить t1/t2 в цепную дробь, значения которой будут всё точнее приближать требуемое отношение. Самое интересное, что так можно аппроксимировать не только иррациональное, но и "сложное" рациональное число более "простой" дробью (с меньшим знаменателем).
Для числа 1336/941 получаем приближения 1, 3/2, 7/5, 10/7, 17/12 и т. д.
Теория цепных дробей всё же имеет отношение к музыке - она хорошо описывает периодические паттерны, которые человек слышит в одновременно звучащих тонах (или ритмах), или видит в наложенных периодических решётках (муар) и т.д.

NutsUnderline
26.11.2023 01:52ну чтож, автор открыл для себя "хорошо забытое старое", и навесил кликбейтный заголовок.
Для меня вот например вполне себе "открытием" здесь является картинка с синусом и треугольником - я вполне знаю про ШИМ, но у меня в голове это представление сугубо "машинное" в виде счетчика. Хотя даже в даташитах значение счетчиков треугольниками рисуют.

aabzel Автор
26.11.2023 01:52+1Задача образования не только в производстве новых знаний, но и в воспроизводстве старых.

nixtonixto
26.11.2023 01:52+2Если вы воспроизводите синус, то вы осциллографом не увидите синус на выходе. Вы его только услышите. Надо еще прикрепить специально рассчитанный фильтр нижних частот.
Пользуйтесь цифровым осциллографом - даже у дешёвых есть настраиваемые ФНЧ/ФВЧ, которые программно удаляют постоянную составляющую и ВЧ-помехи от ШИМа.

vlatro
26.11.2023 01:52+1Вообще не понимаю, зачем ехать в Париж через Чукотку. Засэмплировать по одному периоду отдельных частот и смешивать одну частоту из «нижней» группы с одной из «верхней» группы «на лету». Один цикл while с двумя циклическими счётчиками и одна операция сложения. «Когда деревья были большими» с этим справлялись 8-битные МК с частотой ядра 4МГц ) - правда, если писать на ассемблере ))
А то, что «наименьший общий период» будет «стремиться к бесконечности» - очевидно, там частоты специально подобраны так, чтобы гармоники одной не попадали на другую.

An_private
26.11.2023 01:52+1Засэмплировать по одному периоду отдельных частот
Этот подход плохо работает когда частота дискретизации не слишком велика. Например, 1633Гц при частоте дискретизации 32кГц даст всего 20 семплов на период. То есть фактическая частота сгенерированного сигнала будет 32/20=1.6 кГц. В случае DTMF это не критично, но метод табличного синтеза с интерполяцией не сильно сложнее вычислительно, но даёт куда более точное значение синтезированной частоты.

dlinyj
26.11.2023 01:52+2Классная статья, спасибо. Но слишком уж много опросов в конце, пока долистаешь чтобы поставить плюс устанешь.


miksoft
Нужна пояснительная бригада. На непосвященный взгляд кажется, что 1 секунды достаточно. Ведь частоты целочисленные (в Герцах), значит в секунду укладывается целое число периодов. Или имелось в виду, что по сравнению с памятью микроконтроллера (не нашел упоминания модели в статье) секунда так же велика, как века?
И, похоже, без специальных ухищрений меньший период не годится, т.к. 1336 и 941 не имеют общих делителей.
aabzel Автор
Да. У меня микроконтроллер nrf5340 + куча софта в прошивке уже есть. Ему даже полсекунды не запомнить на Fs 48kHz.