Всем привет!
Давно хотел начать цикл статей, посвященных цифровой обработке сигналов на ПЛИС, но по разным причинам так и не мог к этому приступить. К счастью, в распоряжении появилось немного свободного времени, поэтому периодически я буду публиковать материалы, в которых отражены различные аспекты, связанные с ЦОС на ПЛИС.

В этих статьях я постараюсь минимизировать теоретическое описание тех или иных алгоритмов и большую часть материала посвятить практическим тонкостям, с которыми столкнулся лично я и мои коллеги, и знакомые, так или иначе связанные с разработкой на ПЛИС. Надеюсь, данный цикл статей принесет пользу, как начинающим инженерам, так и матёрым разработчикам.
В первой части рассмотрим простейший CIC фильтр. CIC – «cascaded integral-comb», по-русски – каскадный интегрально-гребенчатый фильтр типа БИХ (с бесконечной импульсной характеристикой). Класс таких фильтров широко используется в задачах, где требуется работа на нескольких скоростях передачи данных. CIC фильтры активно применяются для децимации и интерполяции, то есть для понижения и повышения частоты дискретизации. CIC фильтр сам по себе есть не что иное, как фильтр нижних частот (ФНЧ). То есть такой фильтр пропускает нижние частоты спектра, обрубая верхние за частотой среза. АЧХ фильтра строится по закону ~sin(x)/x. Главное преимущество CIC фильтров состоит в том, что они совсем не требуют операций умножения (в отличие от другого типа фильтров, например, КИХ).
Из названия можно догадаться, что в основе CIC фильтра лежит два базовых блока: интегратор и гребенчатый фильтр (дифференциатор). Интегрирующее звено (int) представляет собой обычный БИХ-фильтр первого порядка, выполненный как самый простой аккумулятор. Гребенчатый фильтр (comb) является КИХ-фильтром первого порядка.
Между интегратором и гребенчатым фильтром часто ставится узел повышения или понижения частоты дискретизации в целое число раз — R.
Формулы для передаточной и амплитудно-частотной характеристик приведены ниже:

Более подробно со всеми математическими выкладками обо всех аспектах децимации и интерполяции можно почитать в других источниках, на которые в конце статьи я приведу ссылки.
Если CIC-фильтр используется для понижения частоты дискретизации, то он называется дециматором. В таком случае первым звеном идет интегратор, затем происходит понижение частоты дискретизации и, наконец, идет звено дифференцирующего фильтра.
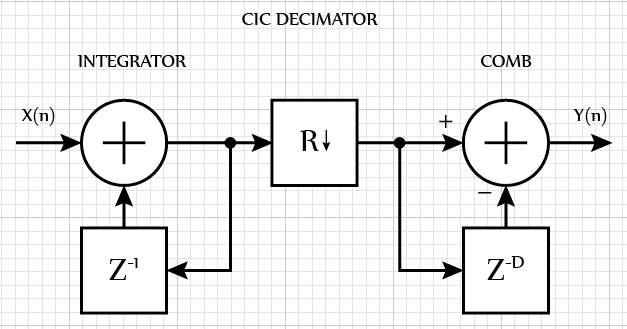
Если CIC-фильтр используется для повышения частоты дискретизации, то он называется интерполятором. В таком случае дифференцирующее звено стоит на первом месте, затем происходит повышение частоты дискретизации и, наконец, идет звено интегрирующего фильтра.
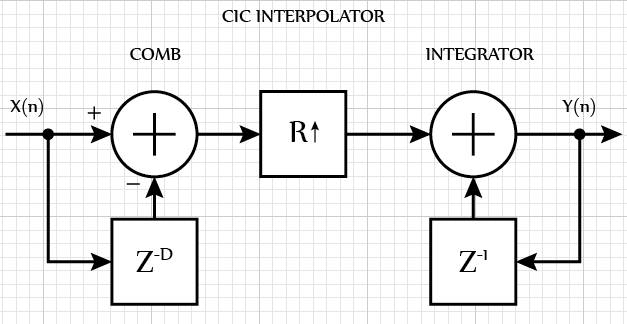
В зависимости от задержки входного сигнала в дифференцирующем звене, можно получать различные частотные характеристики фильтра. Известно, что при увеличении параметра задержки D, увеличивается количество «нулей» амплитудно-частотной характеристики (АЧХ) фильтра.
Заметим, что для связки интегратора и гребенчатого фильтра (CIC фильтра) при увеличении параметра D в дифференцирующей секции нули АЧХ смещаются к центру – изменяется частота среза фильтра Fc = 2 pi / D.
Каскадное соединение интегратора и гребенчатого фильтра без операций децимации и интерполяции называется фильтром «скользящего среднего». Уровень первого бокового лепестка такого фильтра составляет всего -13 дБ, что достаточно мало для серьезных задач ЦОС.
В силу линейности математических операций, происходящих в CIC фильтре возможно каскадное соединение нескольких фильтров подряд. Это дает пропорциональное уменьшение уровня боковых лепестков, но также увеличивает завал главного лепестка спектра (под спектром я часто буду понимать АЧХ фильтра). Таким образом, при N-каскадном соединении однотипных CIC фильтров происходит перемножение идентичных передаточных характеристик. Как правило, секции интеграторов и гребенчатых фильтров объединяются вместе по типу. Например, сначала последовательно ставится N секций однотипных интеграторов, затем N секций однотипных дифференцирующих фильтров.
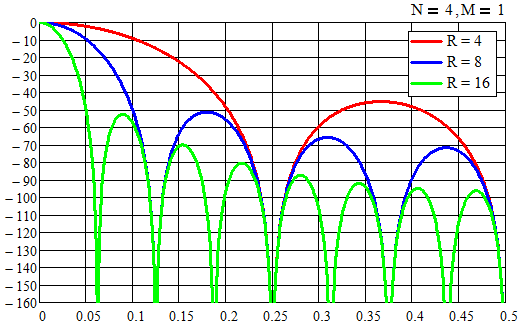
На следующем рисунке приведена АЧХ фильтра при различных параметрах коэффициента дискретизации R (расчет сделан в MathCAD 14).
АЧХ CIC фильтра полностью эквивалентна частотной характеристике FIR фильтра с прямоугольной импульсной характеристикой (ИХ). Общая ИХ фильтра определяется как свертка всех импульсных характеристик каскадов связки интегратора и гребенчатого фильтра. С ростом порядка CIC фильтра, его ИХ интегрируется соответствующее число раз. Таким образом, для CIC фильтра первого порядка ИХ – прямоугольник, для фильтра второго порядка ИХ – равнобедренный треугольник, для третьего порядка ИХ – парабола и т.д.
К несчастью, увеличение величины задержки D в гребенчатой структуре и увеличение порядка фильтра N приводят к росту коэффициента передачи. Это в свою очередь приводит к увеличению разрядности на выходе фильтра. В задачах ЦОС, где применяются CIC фильтры нужно всегда об этом помнить и следить, чтобы передаваемые сигналы не выходили за используемую разрядную сетку. К примеру, негативный эффект роста разрядности проявляется в значительном увеличении используемых ресурсов кристалла ПЛИС.
Интерполятор: использование ограниченной точности не влияет на внутреннюю разрядность регистров, масштабируется только последний выходной каскад. Существенный рост разрядности данных происходит в секциях интеграторов.
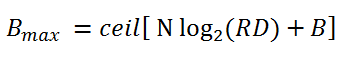
Дециматор: CIC фильтр-дециматор очень чувствителен к параметрам D, R и N, от которых зависит разрядность промежуточных и выходных данных. И дифференцирующее звено, и интегратор влияют на конечную разрядность выходного сигнала.
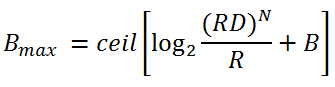
В этих формулах: B — разрядность входных данных, Bmax — разрядность выходных данных, R — коэффициент дискретизации, D — параметр задержки, N — порядок фильтра (количество каскадов).
Замечание! В статье Хогенауэра описаны принципы выбора разрядности для каждого каскада дециматора. Xilinx и Altera при реализации своих фильтров учитывают негативный эффект роста разрядности фильтра и борятся с этим явлением методами, описанными в статье.
Так как я моя работа на 99% связана с микросхемами фирмы Xilinx, я приведу описание IP-ядра фильтра для этого вендора. Но смею вас заверить, что для Altera все практически аналогично.
Для того, чтобы создать CIC фильтр, необходимо зайти в приложение CORE Generator и создать новый проект, в котором указать тип используемого кристалла ПЛИС и различные другие несущественные в данном случае настройки.
CIC Compiler — Вкладка 1:

Component name имя компонента (используются латинские буквы a-z, цифры 0-9 и символ "_").
Filter Specification:
Sample Rate Change Specification:
Hardware Oversampling Specification: эти параметры влияют на выходную частоту дискретизации, количество тактов, требуемых для обработки данных. От этих параметров также зависит уровень параллелизма внутри ядра и количество занимаемых ресурсов.
* — диапазон зависит от общих настроек и коэффициента дискретизации R.
CIC Compiler — Вкладка 2:
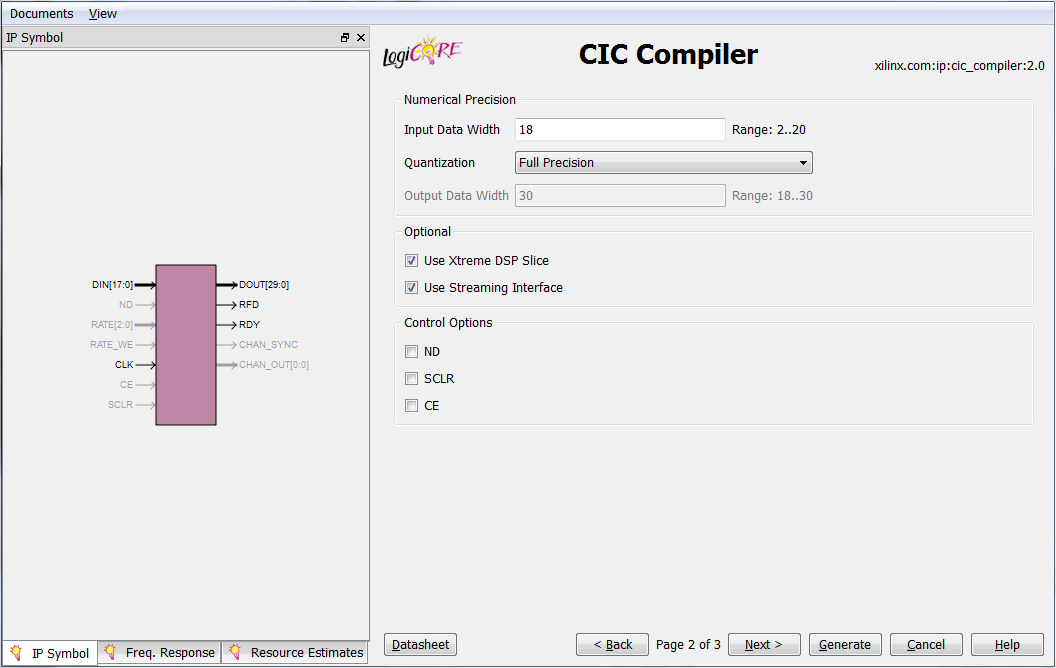
Numerical Precision:
Optional:
Control Options:
CIC Compiler — Вкладка 3:

Summary — эта вкладка в виде списка отражает конечные настройки фильтра (количество каскадов, параметры частот, разрядность входных, выходных и промежуточных данных, задержка в фильтре и т.д.).
В левой части окна CIC Compiler есть три полезные дополнительные вкладки:
После установки всех настроек необходимо нажать на кнопку Generate. В результате приложение CORE Generator через какое-то время выдаст целый набор файлов, из которых нам нужны самые основные:
Если вы работаете в среде ISE Design Suite, то CORE Generator автоматически создаст нужные файлы в рабочем каталоге. Для других средств разработки (типа Modelsim или Aldec Active-HDL) необходимо перенести нужные файлы в соответствующий рабочий каталог.
Пример 1: Для моделирования очень удобным средством является программа MATLAB. Для примера возьмем модель CIC-фильтра 4 порядка, сделанного на логических элементах из System Generator Toolbox от Xilinx. Децимация и интерполяция не используется (CIC вырождается в фильтр скользящего среднего с окном 16). Параметры фильтра: R = 1, N = 4, D = 16. На следующем рисунке приведена модель одного каскада в среде MATLAB.

Посмотрим, как выглядит импульсная характеристика после каждого каскада фильтра, для этого подадим на вход системы периодический единичный импульс.
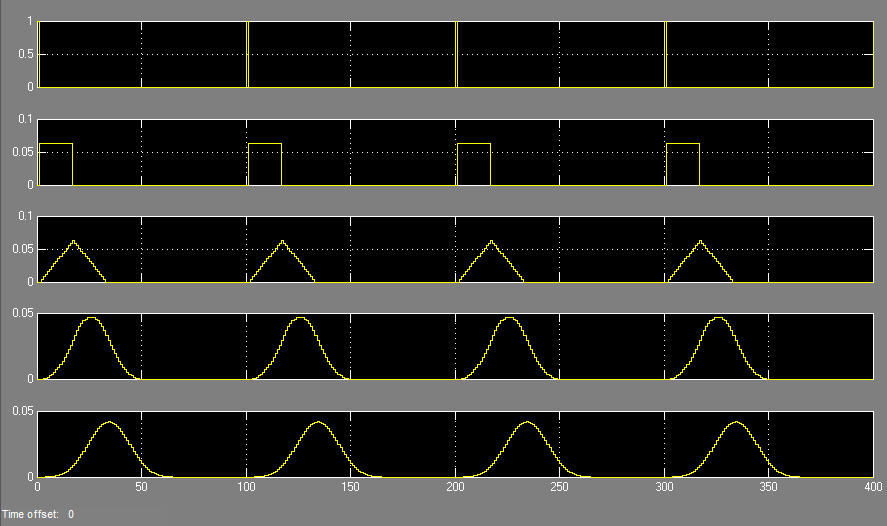
Видно, что сигнал на выходе первого звена образует прямоугольный импульс длительностью = D, на выходе второго звена — треугольный сигнал длительностью 2D, на выходе третьего звена — параболический импульс, на выходе третьего — кубическая парабола. Результат полностью согласуется с теорией.
Пример 2: непосредственно IP-ядро CIC фильтра. Параметры: N = 3, R = 4, D = 1. На следующем рисунке представлена модель фильтра.
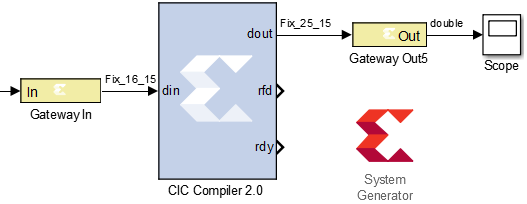
Если на вход такого фильтра подать единичный импульс длительностью несколько тактов (например 32), то на выходе образуется сигнал параболической формы, напоминающий ИХ фильтра скользящего среднего третьего порядка.

Резюме
На этом хотелось бы подвести итог. CIC фильтры используются во многих задачах, где требуется изменить частоту дискретизации. CIC фильтры применяются в системах, работающих на нескольких частотах дискретизации (multirate processing), например, в аудио-технике для изменения бит-рейта (из 44.1кГц в 48кГц и обратно). CIC фильтры применяются в системах связи для реализации DDC (digital down converter) и DUC (digital up converters). Пример использования CIC-фильтров: микросхема цифрового приема AD6620 от Analog Devices.
Реализация собственного фильтра на ПЛИС на HDL языках часто не требуется, и можно смело пользоваться готовыми ядрами от вендоров, либо готовыми opensource-проектами. Если все же возникла необходимость в реализации собственного CIC фильтра для прикладной задачи, то нужно помнить следующие принципы.
CIC фильтры обладают рядом особенностей:
Литература
Продолжение следует...
Давно хотел начать цикл статей, посвященных цифровой обработке сигналов на ПЛИС, но по разным причинам так и не мог к этому приступить. К счастью, в распоряжении появилось немного свободного времени, поэтому периодически я буду публиковать материалы, в которых отражены различные аспекты, связанные с ЦОС на ПЛИС.

В этих статьях я постараюсь минимизировать теоретическое описание тех или иных алгоритмов и большую часть материала посвятить практическим тонкостям, с которыми столкнулся лично я и мои коллеги, и знакомые, так или иначе связанные с разработкой на ПЛИС. Надеюсь, данный цикл статей принесет пользу, как начинающим инженерам, так и матёрым разработчикам.
Часть 1: CIC фильтр
В первой части рассмотрим простейший CIC фильтр. CIC – «cascaded integral-comb», по-русски – каскадный интегрально-гребенчатый фильтр типа БИХ (с бесконечной импульсной характеристикой). Класс таких фильтров широко используется в задачах, где требуется работа на нескольких скоростях передачи данных. CIC фильтры активно применяются для децимации и интерполяции, то есть для понижения и повышения частоты дискретизации. CIC фильтр сам по себе есть не что иное, как фильтр нижних частот (ФНЧ). То есть такой фильтр пропускает нижние частоты спектра, обрубая верхние за частотой среза. АЧХ фильтра строится по закону ~sin(x)/x. Главное преимущество CIC фильтров состоит в том, что они совсем не требуют операций умножения (в отличие от другого типа фильтров, например, КИХ).
Введение
Из названия можно догадаться, что в основе CIC фильтра лежит два базовых блока: интегратор и гребенчатый фильтр (дифференциатор). Интегрирующее звено (int) представляет собой обычный БИХ-фильтр первого порядка, выполненный как самый простой аккумулятор. Гребенчатый фильтр (comb) является КИХ-фильтром первого порядка.
Между интегратором и гребенчатым фильтром часто ставится узел повышения или понижения частоты дискретизации в целое число раз — R.
- В случае понижения частоты дискретизации из входной последовательности выбирается каждый R-отсчет, образуя прореженную выходную последовательность.
- В случае повышения частоты дискретизации между отсчетами входной последовательности просто вставляются нули, которые затем сглаживаются в интегрирующей секции, образуя последовательность на увеличенной частоте дискретизации.
Формулы для передаточной и амплитудно-частотной характеристик приведены ниже:

Более подробно со всеми математическими выкладками обо всех аспектах децимации и интерполяции можно почитать в других источниках, на которые в конце статьи я приведу ссылки.
Дециматор
Если CIC-фильтр используется для понижения частоты дискретизации, то он называется дециматором. В таком случае первым звеном идет интегратор, затем происходит понижение частоты дискретизации и, наконец, идет звено дифференцирующего фильтра.

Интерполятор
Если CIC-фильтр используется для повышения частоты дискретизации, то он называется интерполятором. В таком случае дифференцирующее звено стоит на первом месте, затем происходит повышение частоты дискретизации и, наконец, идет звено интегрирующего фильтра.

В зависимости от задержки входного сигнала в дифференцирующем звене, можно получать различные частотные характеристики фильтра. Известно, что при увеличении параметра задержки D, увеличивается количество «нулей» амплитудно-частотной характеристики (АЧХ) фильтра.
Заметим, что для связки интегратора и гребенчатого фильтра (CIC фильтра) при увеличении параметра D в дифференцирующей секции нули АЧХ смещаются к центру – изменяется частота среза фильтра Fc = 2 pi / D.
Каскадное соединение интегратора и гребенчатого фильтра без операций децимации и интерполяции называется фильтром «скользящего среднего». Уровень первого бокового лепестка такого фильтра составляет всего -13 дБ, что достаточно мало для серьезных задач ЦОС.
В силу линейности математических операций, происходящих в CIC фильтре возможно каскадное соединение нескольких фильтров подряд. Это дает пропорциональное уменьшение уровня боковых лепестков, но также увеличивает завал главного лепестка спектра (под спектром я часто буду понимать АЧХ фильтра). Таким образом, при N-каскадном соединении однотипных CIC фильтров происходит перемножение идентичных передаточных характеристик. Как правило, секции интеграторов и гребенчатых фильтров объединяются вместе по типу. Например, сначала последовательно ставится N секций однотипных интеграторов, затем N секций однотипных дифференцирующих фильтров.
На следующем рисунке приведена АЧХ фильтра при различных параметрах коэффициента дискретизации R (расчет сделан в MathCAD 14).

АЧХ CIC фильтра полностью эквивалентна частотной характеристике FIR фильтра с прямоугольной импульсной характеристикой (ИХ). Общая ИХ фильтра определяется как свертка всех импульсных характеристик каскадов связки интегратора и гребенчатого фильтра. С ростом порядка CIC фильтра, его ИХ интегрируется соответствующее число раз. Таким образом, для CIC фильтра первого порядка ИХ – прямоугольник, для фильтра второго порядка ИХ – равнобедренный треугольник, для третьего порядка ИХ – парабола и т.д.
Рост разрядности данных
К несчастью, увеличение величины задержки D в гребенчатой структуре и увеличение порядка фильтра N приводят к росту коэффициента передачи. Это в свою очередь приводит к увеличению разрядности на выходе фильтра. В задачах ЦОС, где применяются CIC фильтры нужно всегда об этом помнить и следить, чтобы передаваемые сигналы не выходили за используемую разрядную сетку. К примеру, негативный эффект роста разрядности проявляется в значительном увеличении используемых ресурсов кристалла ПЛИС.
Интерполятор: использование ограниченной точности не влияет на внутреннюю разрядность регистров, масштабируется только последний выходной каскад. Существенный рост разрядности данных происходит в секциях интеграторов.
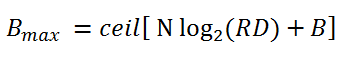
Дециматор: CIC фильтр-дециматор очень чувствителен к параметрам D, R и N, от которых зависит разрядность промежуточных и выходных данных. И дифференцирующее звено, и интегратор влияют на конечную разрядность выходного сигнала.
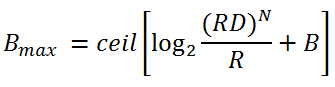
В этих формулах: B — разрядность входных данных, Bmax — разрядность выходных данных, R — коэффициент дискретизации, D — параметр задержки, N — порядок фильтра (количество каскадов).
Замечание! В статье Хогенауэра описаны принципы выбора разрядности для каждого каскада дециматора. Xilinx и Altera при реализации своих фильтров учитывают негативный эффект роста разрядности фильтра и борятся с этим явлением методами, описанными в статье.
Xilinx CIC Filter
Так как я моя работа на 99% связана с микросхемами фирмы Xilinx, я приведу описание IP-ядра фильтра для этого вендора. Но смею вас заверить, что для Altera все практически аналогично.
Для того, чтобы создать CIC фильтр, необходимо зайти в приложение CORE Generator и создать новый проект, в котором указать тип используемого кристалла ПЛИС и различные другие несущественные в данном случае настройки.
CIC Compiler — Вкладка 1:

Component name имя компонента (используются латинские буквы a-z, цифры 0-9 и символ "_").
Filter Specification:
- Filter type — тип фильтра: интерполирующий / децимирующий.
- Number of stages — количество каскадов интеграторов и гребенчатых фильтров: 3-6.
- Differential delay — задержка в дифференциальных ячейках фильтра: 1-2.
- Number of channels — количество независимых каналов: 1-16.
Sample Rate Change Specification:
- Fixed / Programmable — тип коэффициента дискретизации R: постоянный / программируемый.
- Fixed or Initial Rate — значение коэффициента дискретизации R: 4..8192.
- Minimum Rate — минимальное значение коэффициента дискретизации R: 4..8.
- Maximum Rate — максимальное значение коэффициента дискретизации R: 8..8192.
Hardware Oversampling Specification: эти параметры влияют на выходную частоту дискретизации, количество тактов, требуемых для обработки данных. От этих параметров также зависит уровень параллелизма внутри ядра и количество занимаемых ресурсов.
- Select format — выбор частотных соотношений фильтра: Frequency Specification / Sample period.
- Frequency Specification — Частотная спецификация: пользователь задает частоту дискретизации и частоту обработки данных.
- Sample period — Тактовая спецификация: пользователь задает отношение частоты обработки к тактовой частоте данных.
- Input Sampling Frequency — входная частота дискретизации: *.
- Clock frequency — частота обработки фильтра: *.
- Input Sampling period — отношение частоты обработки к частоте входного тактового сигнала: *.
* — диапазон зависит от общих настроек и коэффициента дискретизации R.
CIC Compiler — Вкладка 2:

Numerical Precision:
- Input Data Width — разрядность входных данных: 2..20.
- Quantization — округление выходных данных: полная точность / округление разрядной сетки.
- Output Data Width — разрядность выходных данных, диапазон зависит от коэффициентов N, D и R (максимальное значение — 48 битов).
Optional:
- Use Xtreme DSP Slice — использовать встроенные DSP-блоки для реализации фильтра.
- Use Streaming Interface — использовать потоковый интерфейс для многоканальной реализации фильтра.
Control Options:
- ND — «New data», входной сигнал, определяющий поступление данных на вход фильтра.
- SCLR — синхронный сброс фильтра (логическая единица на этом входе производит сброс).
- CE — «Clock Enable», сигнал разрешения тактирования фильтра.
CIC Compiler — Вкладка 3:

Summary — эта вкладка в виде списка отражает конечные настройки фильтра (количество каскадов, параметры частот, разрядность входных, выходных и промежуточных данных, задержка в фильтре и т.д.).
В левой части окна CIC Compiler есть три полезные дополнительные вкладки:
- IP-symbol — схематичный вид IP-блока с активными портами ввода/вывода.
- Freq. response — передаточная характеристика CIC-фильтра.
- Resource estimate — оценка занимаемых ресурсов.
После установки всех настроек необходимо нажать на кнопку Generate. В результате приложение CORE Generator через какое-то время выдаст целый набор файлов, из которых нам нужны самые основные:
- *.VHD (или *.V) — файл исходных кодов для моделирования на VHDL или Verilog.
- *.VHO — бесполезный файл, но из него можно взять описание компонента и портирование для вставки в проект.
- *.NGC — файл списка соединений. Содержит описание архитектуры IP-ядра (используемые компоненты и связи сигналов между ними) для выбранного кристалла ПЛИС.
- *.XCO — лог-файл, в котором хранятся все параметры и настройки IP-ядра. Полезный файл при работе в среде Xilinx ISE Design Suite.
Если вы работаете в среде ISE Design Suite, то CORE Generator автоматически создаст нужные файлы в рабочем каталоге. Для других средств разработки (типа Modelsim или Aldec Active-HDL) необходимо перенести нужные файлы в соответствующий рабочий каталог.
CIC Filter in MATLAB
Пример 1: Для моделирования очень удобным средством является программа MATLAB. Для примера возьмем модель CIC-фильтра 4 порядка, сделанного на логических элементах из System Generator Toolbox от Xilinx. Децимация и интерполяция не используется (CIC вырождается в фильтр скользящего среднего с окном 16). Параметры фильтра: R = 1, N = 4, D = 16. На следующем рисунке приведена модель одного каскада в среде MATLAB.

Посмотрим, как выглядит импульсная характеристика после каждого каскада фильтра, для этого подадим на вход системы периодический единичный импульс.

Видно, что сигнал на выходе первого звена образует прямоугольный импульс длительностью = D, на выходе второго звена — треугольный сигнал длительностью 2D, на выходе третьего звена — параболический импульс, на выходе третьего — кубическая парабола. Результат полностью согласуется с теорией.
Пример 2: непосредственно IP-ядро CIC фильтра. Параметры: N = 3, R = 4, D = 1. На следующем рисунке представлена модель фильтра.

Если на вход такого фильтра подать единичный импульс длительностью несколько тактов (например 32), то на выходе образуется сигнал параболической формы, напоминающий ИХ фильтра скользящего среднего третьего порядка.

Резюме
На этом хотелось бы подвести итог. CIC фильтры используются во многих задачах, где требуется изменить частоту дискретизации. CIC фильтры применяются в системах, работающих на нескольких частотах дискретизации (multirate processing), например, в аудио-технике для изменения бит-рейта (из 44.1кГц в 48кГц и обратно). CIC фильтры применяются в системах связи для реализации DDC (digital down converter) и DUC (digital up converters). Пример использования CIC-фильтров: микросхема цифрового приема AD6620 от Analog Devices.
Реализация собственного фильтра на ПЛИС на HDL языках часто не требуется, и можно смело пользоваться готовыми ядрами от вендоров, либо готовыми opensource-проектами. Если все же возникла необходимость в реализации собственного CIC фильтра для прикладной задачи, то нужно помнить следующие принципы.
CIC фильтры обладают рядом особенностей:
- Простые в реализации и не требуют операций умножения.
- Децимация и интерполяция на CIC фильтрах используется повсеместно для быстрого изменения частоты дискретизации, как в целое, так и в дробное число раз.
- С ростом порядка фильтра N и величины задержки D увеличивается разрядность промежуточных и выходных данных.
- С ростом порядка фильтра N увеличивается подавление боковых лепестков и увеличивается неравномерность главного лепестка АЧХ.
- Рекомендуется использовать фильтры порядка не более 6-8, т.к. с увеличением порядка усложняется реализация, увеличивается объем занимаемых ресурсов, а также происходят искажения АЧХ фильтра в пределах полосы пропускания.
- С ростом параметра задержки D гребенчатого фильтра изменяется частота среза фильтра, но в практических целях при каскадном соединении параметр D < 3.
- При децимации в R раз существенно увеличивается разрядность на выходе фильтра.
- При интерполяции основной вклад в разрядность промежуточных и выходных данных вносят только интегрирующие звенья.
- АЧХ CIC фильтра эквивалентна АЧХ FIR фильтра с прямоугольной импульсной характеристикой. Общая ИХ фильтра определяется как свертка всех импульсных характеристик каскадов связки интегратора и гребенчатого фильтра.
- При изменении частоты на выходе фильтра в ПЛИС используют сигнал разрешения «clock enable», а частоту обработки не изменяют.
- Если отношение «частота обработки / частота дискретизации» >> 1, в ПЛИС возможно повторно использовать ресурсы фильтра, тем самым для многоканальной системы реализовать обработку с минимальной затратой ресурсов кристалла.
- В современных ПЛИС CIC фильтры реализуются на блоках DSP (Xilinx, Altera), но при отсутствии свободных ресурсов возможна реализация на логических ячейках (SLICEs).
- После CIC фильтра рекомендуется ставить умножитель с программируемым коэффициентом усиления (gain multiplier), который будет подстраивать уровень сигнала до нужного динамического диапазона
- CIC фильтры вносят искажение в спектр выходного сигнала, поэтому после CIC фильтра необходимо ставить компенсирующий FIR фильтр (методика расчета представлена в даташите Altera, для расчета необходим MATLAB).
Литература
- E. Ifeachor, B. Jervis. Digitaal l SignProcessing: A Practical Approach (2nd Edition).
- Hogenauer, E. An economical class of digital filters for decimation and interpolation.
- Wikipedia CIC filter
- Altera CIC Filter Userguide
- Xilinx CIC Compiler DS613
- MATLAB CIC Filter
- DSPLIB — CIC фильтры
- DSPLIB — CIC дециматор и интерполятор
- Исходные коды на Verilog с пояснениями
- OpenCores project 1. Фамилия у автора очень интересная :)
- OpenCores project 2
Продолжение следует...
Комментарии (12)

mezastel
04.12.2015 18:26Почему этот пост не на Хабре?

capitanov
04.12.2015 19:00С хабра тематика FPGA давно переехала на гиктаймс :)

mezastel
04.12.2015 19:04Ээээ… точно? Точно не «давно», еще недавно видел там посты Метротека. И интересно почему же? Хабр гиковый ресурс, место FPGA там.

capitanov
04.12.2015 19:49Мою первую статью, написанную на хабре, в свое время переместили сюда. Поищите на гиктаймс по метке или хабу "fpga" статьи — они практически все тут.

Alexeyslav
06.12.2015 00:40Просто надо иметь в виду что раздел происходит не по тому что именно описано в статье а как именно. Практические конструкции вроде DIY — на гиктаймсе, а Хабр больше для профессиональных теоретических статей, из которых не выходят практические конструкции а раскрывается теория. По этому критерию статье самое место именно на хабре.


nerudo
Тут есть нюанс. Насколько я понимаю, изменение частоты дискретизации возможно только между кратными частотами. Т.е. для комбинации частот 44.1 и 48 нужно получить промежуточную частоту (весьма высокую для столь неудачной комбинации — 2822,4 кГц). В целом же, для передискретизации между некратными частотами используются farrow-фильтры
0serg
Это широко распространенное заблуждение. Во-первых наивная передискретизация сигнала кратной частоты, к примеру усреднением двух подряд идущих отсчетов для снижения частоты дискретизации вдвое создаст проблемы. Во-вторых при понимании почему такое происходит становится очевидно что никаких ограничений на «кратность частот» на самом деле нет. Кратность влияет сугубо на удобство обработки, у кратных частот вычисления можно значительно упростить.
nerudo
Мы вроде [в контексте данного топика] говорим конкретно про CIC-структуру, а не «фильтры вообще». Я, честно говоря, слабо понимаю, как с помощью классического CIC изменить частоту дискретизации на 8.83% (естественно без внесения существенных искажений в сигнал) не поднимая частоту обработки выше большей из частот.
0serg
Да, это верно, согласен. Слишком просто часто вижу этот комментарий в общем контексте.
capitanov
Мне кажется, что для современных ПЛИС использовать «большие» частоты дискертизации при обработке звука — ерунда. Например, поставить интерполятор на R(I) = 160, а затем дециматор на R(D) = 147 — не проблема. Частота обработки в любом случае будет много выше частоты дискретизации. Другов вопрос, что делать преобразование из 44.1 в 48 на таких ПЛИС как Kintex-7 или Stratix V не имеет смысла.
nerudo
Именно.