Итак, функции активации. Что мы знаем о них помимо загадочной тайны просто ужасных соглашений о наименованиях (о чем поговорим позже ????) и зачем они нам нужны?

Идея, собственно, настолько проста, что даже ваш кот может разобраться в этом. Прежде всего, что-то похожее есть в наших головах. Для этого давайте взглянем на упрощенный нейрон (органический и искусственный):

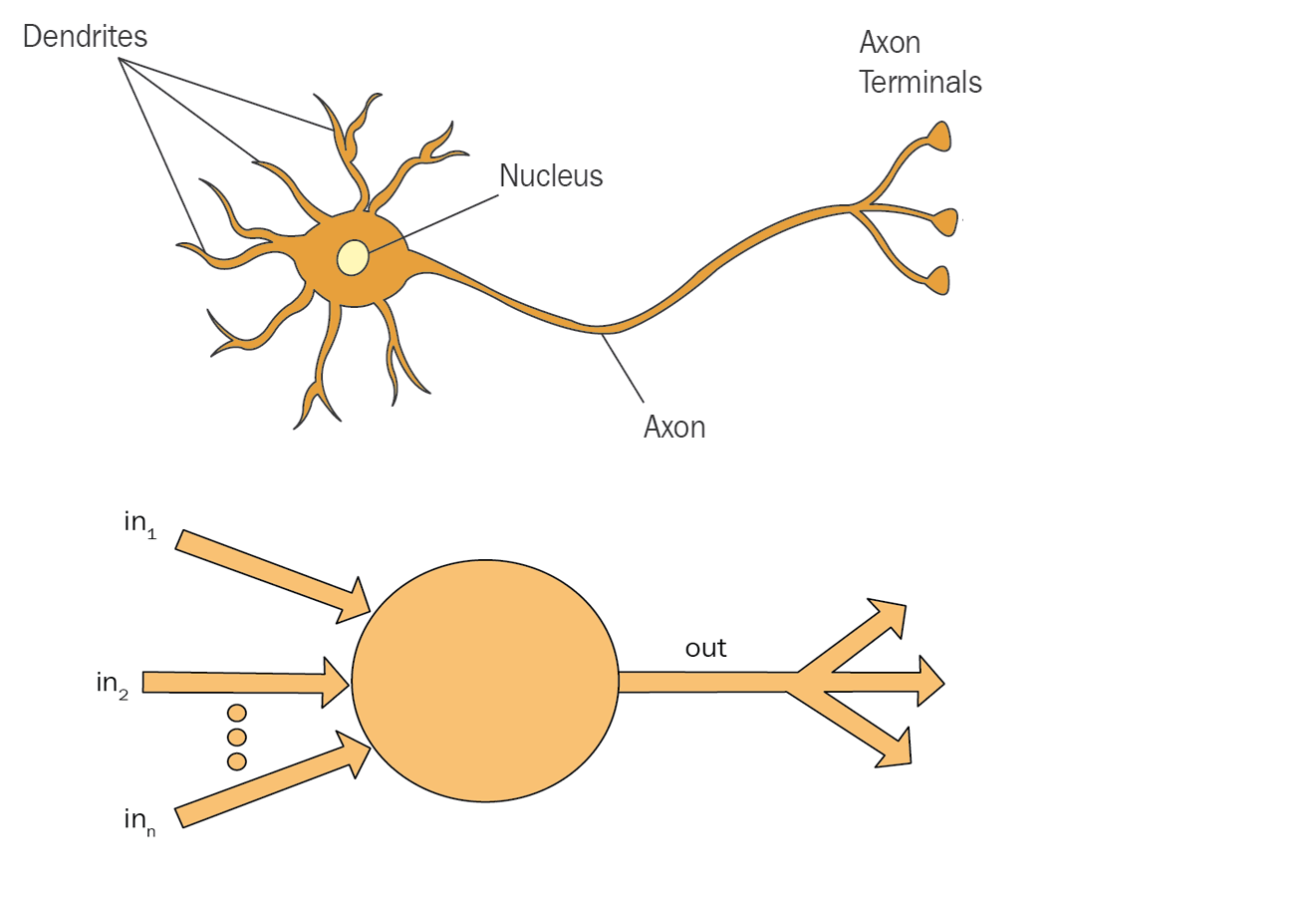
Нейрон принимает множество входных сигналов и магическим образом обрабатывает их, чтобы получить (в идеале) полезный результат на выходе. Поскольку нейроны связаны друг с другом, этот результат может быть передан связанному нейрону в качестве входных данных. Таким образом формируется сеть.

Нейрон внутри просто вычисляет взвешенную сумму своих входных данных. Вот и вся магия - берем все сигналы (которые выражены числами) и суммируем их - это результат. Ключевое слово здесь - "взвешенная" сумма. Он умножает все входные данные на определенный параметр, называемый весом. Как мы обсудили в этой статье, веса вычисляются в процессе обучения, и это главная цель обучения. Таким образом веса, в целом, это магические числа, полученные эмпирическим путем (он же метод тыка).

Искусственный нейрон имеет два основных свойства: weight (вес) и bias (????предвзятость, судья и здесь подкуплен. На самом деле это смещение - подробнее в конце). И все, что он делает, - это линейное преобразование всех входных данных, подобное следующему:

y = a * x + b     # думаю вы узнали уравнение прямой, отсюда название “линейная”

или

output_1 = weight * input_1 + bias

Полная формула выглядит так:

или

output = sum(weight * inputs + bias)

Что нейрон делает кажется простым. Потому что это и правда просто. Но есть один подвох: это слишком просто! Вы можете объединить множество таких нейронов в сеть, но это не поможет - многие сложные процессы в реальной жизни не являются линейными и смоделировать их такой сетью не выйдет! ????

Чтобы обойти это ограничение, выходные данные не отправляются как есть, они сначала преобразуются с использованием функции активации. Активационная функция активирует киборгов, которые захватят… ой не в ту книгу поглядел. Функция активации - это своего рода фильтр, который:

• фильтрует неважную информацию и оставляет только важную в определенном формате;

• вводит необходимую нелинейность, позволяя сети учиться и моделировать сложные закономерности.

Так что если подумать об этом - активационные функции усложняют работу нейронов, и это их основная цель ????... Но это логично, они следуют принципу Альберта Эйнштейна: сделайте настолько просто насколько возможно, но не проще.

Итак, полная функция преобразования нейрона выглядит так:

выход = активационная_функция(сумма(вес * вход + смещение))

или

output = activation_function( sum(weight * inputs + bias) )

Типы слоев нейронов и их связь с выбором функции активации 

Нейроны обычно связывают в сеть, наподобие такой:

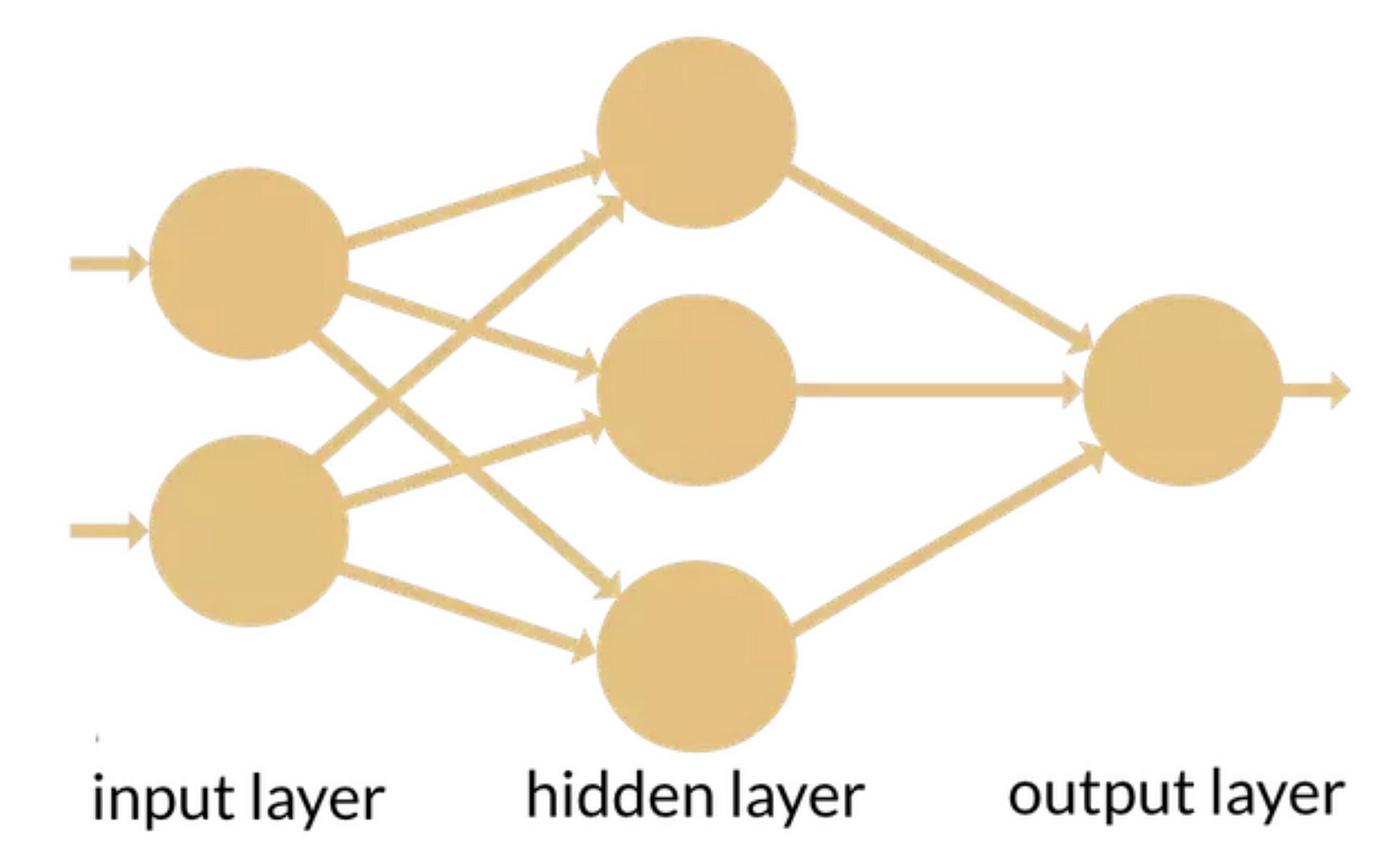
Основные три типа слоев это:

1. Входной - первый слой сети, который принимает сырые данные 

2. Выходной (frontend) — последний слой, который преобразует все что нейронная сеть надумала в более или менее конкретный ответ. Например, если в выходном слое используется softmax — он выдаст вероятности что заданная картинка это собака, кошка или попугай.

3. Скрытый (backend) — бэкенд он и есть бэкенд. Делает всю реальную работу под капотом.

Различные слои используют разные функции активации, потому что у них разные цели (почти так же, как разные фреймворки используются для фронтенда и бэкенда). Какую функцию активации использовать, зависит от одного — чего мы хотим добиться. Эта функция может быть любой, на самом деле, но некоторые функции работают лучше. Вот самые распространенные из них:

ReLU

Rectifier linear unit (aka нелинейная функция)

Много умных слов, готовьтесь быть шокированными настоящим жестким матаном:

if input > 0:
  return input
else:
  return 0

И это всё??? ???? Страшное название, очень простая вещь, как всегда в ML ????. Берем входное число и обрезаем его до ноля, если оно отрицательное. Интересно, кто заведует отделом наименований в машинном обучении. Я думаю — те же люди что придумали “вкусно и точка”...

ReLU предпочтительна по следующим причинам:

• Простота и эффективность: ReLU совершает простую математическую операцию max(0, x). Эта простота приводит к быстрым вычислениям.

• Решение проблемы исчезающего градиента (Vanishing Gradient): В глубоких сетях градиенты могут стать очень маленькими, что мешает обучению сети. Для примера посмотрите на другую распространенную функцию сигмоид:

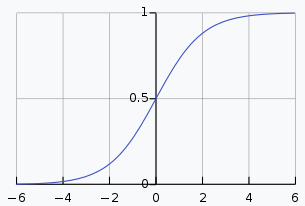
Видите, что она делает? Чем больше значение x, тем ближе y к 1. Это означает, что при очень больших значениях x, когда x изменяется — y практически не меняется. Так что почти не имеет значения, каково значение x после определенного уровня, y будет примерно равно 1, и таким образом система не может реагировать на входные данные, то есть учиться.

Теперь посмотрим на ReLU:

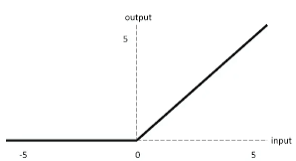
Поскольку у ReLU нет ограничения для всех положительных входных параметров, это помогает уменьшить эту проблему. Однако у ReLU есть и свои недостатки. Самый заметный из них — проблема «умирающего ReLU», когда многие нейроны могут стать неактивными и выводить только ноль, потому что на большом диапазоне значений выход функции равен нулю. Это можно уменьшить с помощью вариаций ReLU, таких как Leaky ReLU или параметрический ReLU (PReLU).

Сигмоида

Раз уж мы начали об этом говорить, давайте рассмотрим еще одно пугающе звучащее инопланетное чудовище. Термин «сигмоид» происходит от греческой буквы «сигма» (Σ, σ), из-за характерной «S»-образной кривой функции. Само слово «сигмоид» по сути означает «S-образный»... Могли бы просто назвать функцию S-образной, знаете... ????‍♂️

Вот график:

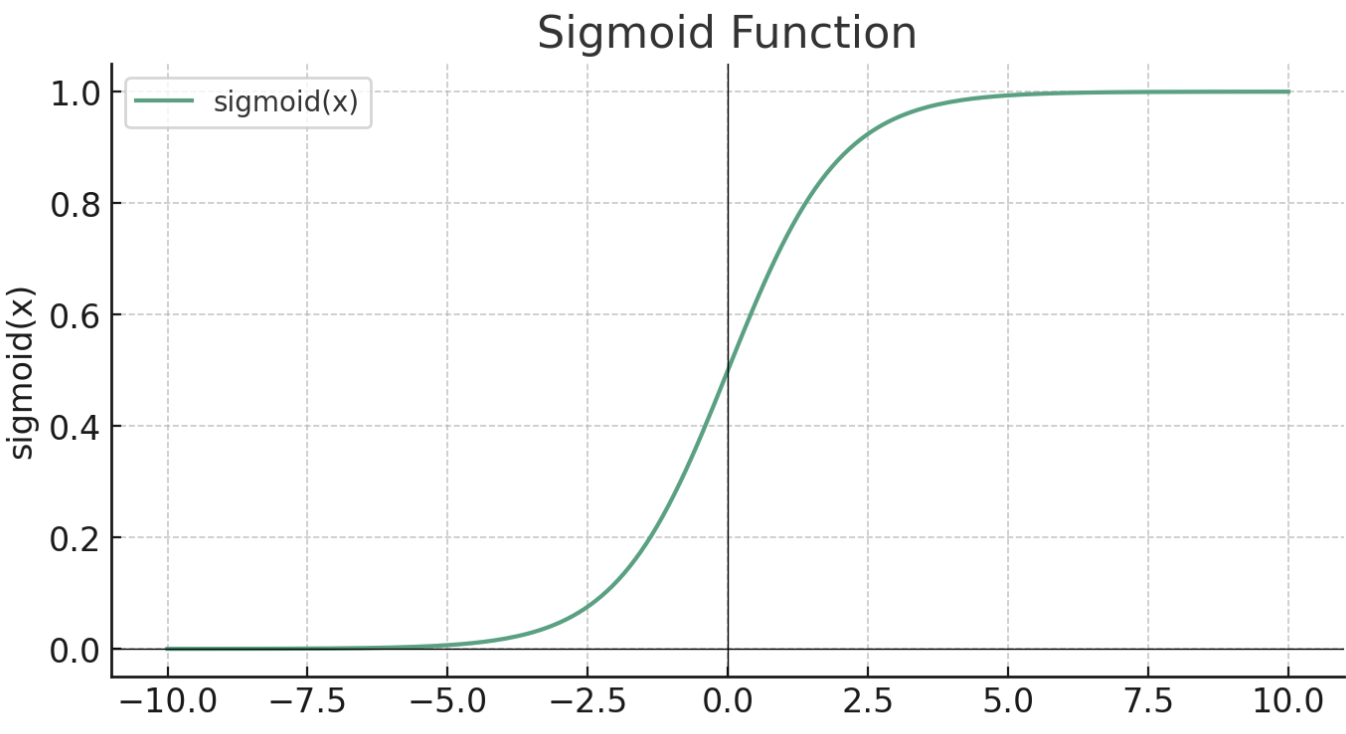
И формула:

f(x) = 1/(1+e^-x)

Сигмоида хороша для бинарной (да/нет) классификации, потому что она принимает любое действительное число в качестве входного и преобразует его в число между 0 и 1. По этой причине она часто используется в выходных слоях (подробнее об этом смотрите в конце).

Softmax

Мягкомаксимум. Как вы уже наверное догадались по предыдущим названиям, эта функция не мягкая и не максимум????. Ну что поделаешь.

Функция softmax принимает на вход вектор из K действительных чисел и нормализует его в распределение вероятностей, состоящее из K вероятностей, пропорциональных экспонентам входных чисел. Да, вы все правильно услышали ????.

Если серьезно, что она делает — принимает список произвольных чисел и преобразует их в список вероятностей пропорциональных этим числам. То есть:

Допустим, у нас есть список [1, 2, 3]:

softmax([1, 2, 3]) = [0.09003, 0.24473, 0.66524]

Вот и все. Сумма возвращаемых вероятностей будет равна 1 (или 100%). Чем больше число во входном списке (по сравнению с другими) — тем выше вероятность, в которую оно будет преобразовано на выходе.

Здесь стоит отметить, что функция принимает вектор (список) входных данных — а не одно число. Это отличается от всех предыдущих, и причина в том, что она работает сразу с несколькими нейронами (обычно со всем слоем). Таким образом, она сворачивает результаты слоя в выходное распределение вероятностей. По этой причине она часто используется в выходных слоях, для получения финального результата.

Кроме того, softmax используется в механизме внимания в архитектуре трансформера, потому что, если подумать, внимание — это своего рода ранжирование множества вещей в список наиболее важных.

Главное, что здесь нужно понять:

• Вероятность того, что входные данные относятся к первой категории (соответствующей 1), составляет примерно 0.09003.

• Вероятность того, что входные данные относятся ко второй категории (соответствующей 2), составляет примерно 0.24473.

• Вероятность того, что входные данные относятся к третьей категории (соответствующей 3), составляет примерно 0.66524.

Это делает функцию softmax особенно полезной для задач классификации в нейронных сетях, когда выходные данные должны представлять вероятность по нескольким классам. Например, когда мы пытаемся понять, является ли изображение собакой (1), кошкой (2) или рыбой (3).

Фактически, если у вас только две категории, она сводится к той же формуле, что и сигмоид, так что она как бы сигмоид только для >2 категорий.

Вот формула, если вы действительно хотите ее увидеть:

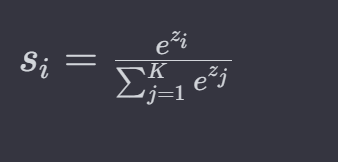
Tanh

Еще один гиперболоид инженера Гарина. Это название хотя бы логичное. Гиперболический тангенс часто сокращается как «tanh» (произносится как «танч»).

Эта функция принимает любое действительное число на входе и выдает значения в диапазоне от -1 до 1:

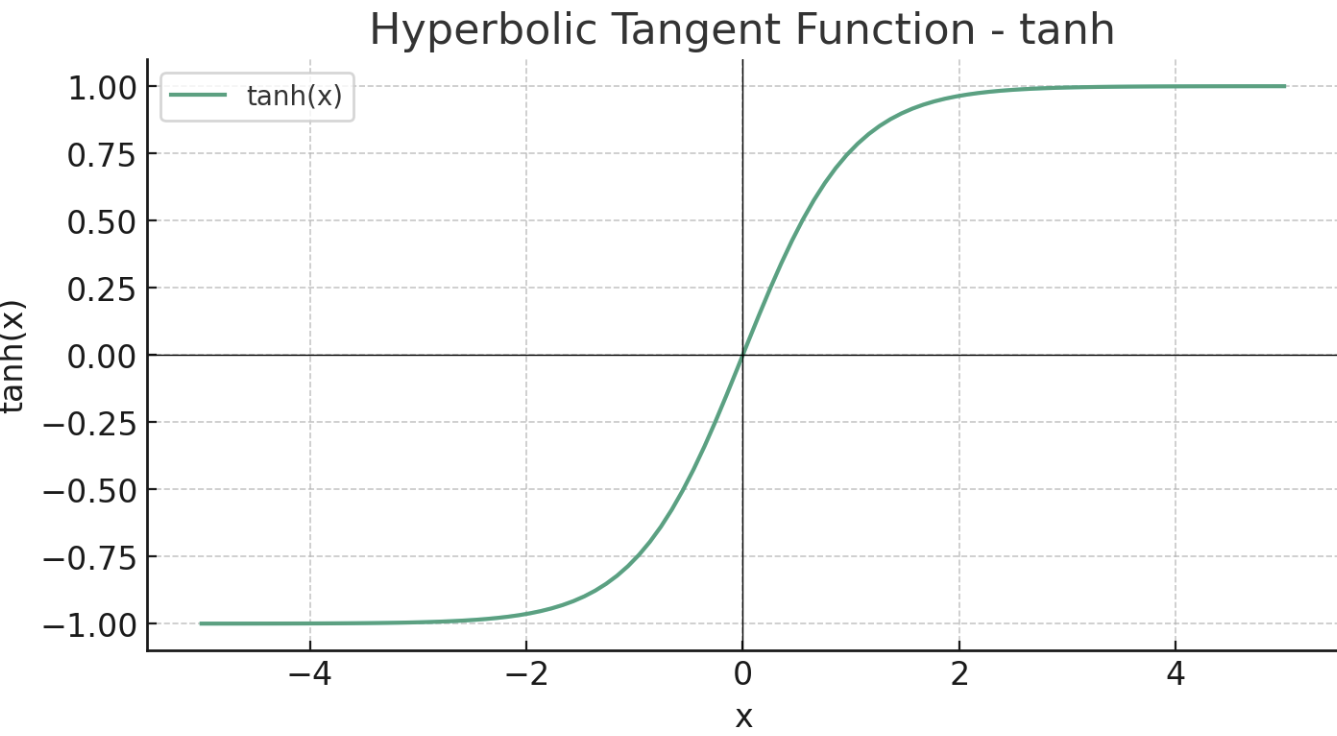
tanh(x) = 2 * sigmoid(2x)-1

или

tanh(x) = 2/(1+e^(-2x)) -1

Выходные значения tanh находятся в диапазоне от -1 до 1, что делает её центрированной относительно нуля. Это выгодно, поскольку это может помочь процессу обучения, так как данные, проходящие через сеть, в среднем будут поддерживать среднее значение близкое к 0, что в свою очередь помогает оптимизации методом градиентного спуска. Выходные значения сигмоида, с другой стороны, не центрированы относительно нуля (диапазон от 0 до 1), что может привести к так называемой проблеме «исчезающих градиентов» (см. раздел ReLU для объяснения). Из-за этих свойств (быстрый градиентный спуск, отсутствие исчезающих градиентов в отличии от сигмоиды) tanh часто используется в скрытых слоях.

Binary Step Function (ступенчатая)

Бинарная ступенчатая функция — один из самых простых типов функций активации, используемых в нейронных сетях. Это пороговая функция активации, которая активируется или нет в зависимости от того, находится ли входное значение x выше или ниже определенного порога, что аналогично переключателю вкл/выкл. Обычно она используется в перцептронах и задачах бинарной классификации, где ожидается, что выход будет либо 0, либо 1, например, при решении, является ли электронное письмо спамом или не спамом.

Исторически это была первая использованная функция активации в контексте нейронных сетей. Она использовалась в самом первом типе искусственного нейрона, названного перцептроном, разработанного Фрэнком Розенблаттом в конце 1950-х годов.

Бинарная ступенчатая функция может быть математически определена как:

где θ это пороговое значение.

Функция не часто используется в современных нейронных сетях, потому что она не дифференцируема на пороге θ, что делает её непригодной для использования с обратным распространением ошибки (методом, используемым для обучения нейронных сетей). Кроме того, она не предоставляет вероятностный результат, а жесткий ответ да-нет, который может быть слишком жестким для реальных задач.

Существует множество других функций, это лишь наиболее часто используемые.

Bias: Поговорим про предвзятость

Ещё одна жертва департамента наименований ????. Очень хочется поглядеть на этих людей и как они называют своих детей…

На самом деле это просто смещение или сдвиг. Название bias пришло из статистики и там оно имеет определенный смысл. Смещение добавляется к сумме входных значений нейрона (собственно чтобы сместить конечный результат), перед применением функции активации.

Это аналог смещения в формуле прямой, позволяет сместить график функции вверх или вниз. Без смещения вывод нейрона полностью управляется суммой входных параметров, что может ограничить его гибкость. Смещение добавляет ещё одну возможность настройки нейрона которая помогает сети лучше подстраиваться под обучающие данные.

Вот пример где смещение одновременно является и предвзятостью. Допустим мы строим рекомендательную систему для фильмов, где мы используем оценки одних пользователей для того чтобы рекомендовать фильмы другим, похожим пользователям. Всегда найдутся особенно привередливые критики, которые никогда не ставят фильмам высоких оценок. Хорошо бы учесть это в нашей системе, но если задуматься - это уже не характеристика фильма, а конкретного пользователя, т.к. он ставит низкие оценки всем фильмам без разбора. Веса зависят от характеристик фильма, а тут что делать? Вот тут и пригождается bias чтобы учесть поправку на особенно привередливых пользователей при обучении модели.

Это все на сегодня, хорошего дня!