Квантовые вычисления / forpes.ru

Главная
Квантовые вычисления

Квантовые вычисления

10.01.2024 08:45

A_Muha 1 3700 Источник

Квантовые вычисления - это наука о хранении и обработке информации с использованием систем, подчиняющихся законам квантовой механики. На атомарном уровне системы проявляют нелогичные эффекты.

Впервые Ричард Фейнман предложил в 1980-х годах, что эти эффекты, возможно, могут быть использованы для выполнения вычислений способом, превосходящим классические вычисления. Вскоре после первого появления квантовых компьютеров были разработаны алгоритмы, которые доказуемо решают определенные задачи быстрее, чем любой известный классический алгоритм. Например, алгоритм Гровера может быть использован для решения задачи неструктурированного поиска по N элементам со сложностью всего O(N). А алгоритм Шора позволяет решить задачу целочисленной факторизации, которая является центральной в системе шифрования RSA с открытым ключом, за полиномиальное время, экспоненциально быстрее, чем наиболее известный классический алгоритм. Моделирование квантово-механических систем является еще одним важным применением квантовых вычислений, которое может обеспечить возможное ускорение по сравнению с классическими алгоритмами.

В частности, моделирование квантово-механических систем сложно для классического компьютера и, по сути, в первую очередь вдохновило концепцию квантового компьютера. Эти ранние теоретические успехи вызвали всплеск исследований в этой области, и тем временем квантовые вычисления превратились в высоко дисциплинарную область исследований на стыке теоретической физики и информатики с теоретической стороны и экспериментальной физики и инженерии с практической.

Далее представим основные компоненты квантовых вычислений. Начнём с описания кубитов, которые являются основными строительными блоками квантовых компьютеров. После объяснения расширения до нескольких кубитов мы обсудим принцип измерения. Наконец, мы представляем концепцию квантовых вентилей. Следующее изложение сосредоточено на ключевых математических концепциях, а также основных примерах.

Кубиты

Кубиты являются базовой единицей в квантовых вычислениях, сравнимой с битами в классических вычислениях. Кубит - это двухуровневое квантовое состояние, то есть двумерный комплексный вектор

$| 0 \rangle = \begin{bmatrix}1\\0\end{bmatrix} , \:| 1 \rangle = \begin{bmatrix}0\\1\end{bmatrix} (1)$

такой, что существуют такие $\alpha$ и $\beta$ , что

$| \psi \rangle = \alpha | 0 \rangle + \beta | 1 \rangle = \begin{bmatrix}\alpha \\\beta\end{bmatrix} (2)$

Эти состояния $| 0 \rangle$ и $| 1 \rangle$ называются базисом состояния и они являются аналогом двух возможных значений классического бита: 0 и 1. Однако, в отличие от классических вычислений, кубит может находиться в суперпозиции. Следовательно в общем случае это линейная комбинация вычислительных базовых состояний, как в (2). Важным явлением, лежащим в основе квантовой механики, является то, что точное значение $| \psi \rangle$ (значения $\alpha$ и $\beta$ ) не могут быть измерены однозначно. Однако когда мы измеряем кубит, результат принимает значения классического бита, то есть значения 0 или 1. Вероятности получения этих результатов равны
$|\alpha|^2$ и $|\beta|^2$ аналогично. Следовательно, $\alpha$ и $\beta$ называются амплитудами вероятности состояния $| \phi \rangle$ . Тот факт, что $| \psi \rangle$ является единичным вектором, согласуется с этой вероятностной интерпретацией, поскольку она подразумевает, что $|\alpha|^2 + |\beta|^2 = 1$ . Тесно связан с этим явлением так называемый «коллапс» кубита после измерения: если измерение возвращает 0 (или 1), то сразу после измерения состояние кубита равно $| 0 \rangle$ (или $| 1 \rangle$ ). Далее в учебном пособии приводится более подробное введение в измерения квантовых состояний.

Обратите внимание, что умножение кубита в состоянии $| \psi \rangle$ на член $e ^{-i\phi}$ (называемый глобальной фазой) с углом $\phi \in R$ не влияет на амплитуды вероятности:

$|e^{-i\phi} \alpha|^2 = |\alpha|^2, \: |e^{-i\phi} \beta|^2 = |\beta|^2 \ (3)$

В частности, глобальная фаза не оказывает никакого влияния на наблюдаемое поведение кубита, поэтому два кубита, которые отличаются глобальной фазой, считаются эквивалентными.

Напомним, что кубит принимает значения в $\mathbb{C}^2$ , который изоморфен $\mathbb{R}^4$ , то есть описывается четырьмя вещественными параметрами. Однако пространство возможных значений кубита может быть параметризовано с использованием только двух реальных параметров: во−первых, как объяснено выше, умножение на глобальную фазу $e ^{-i\phi}$ не изменяет кубит, что уменьшает степени свободы на 1. Во-вторых, кубиты имеют единичную норму, что еще больше ограничивает возможные значения кубитов. В комбинации кубит может быть эквивалентно представлен с использованием только двух вещественных параметров, которые:

$\psi = cos \frac{\theta}{2}| 0 \rangle + e^{i\phi} sin \frac{\theta}{2}| 1 \rangle, \: (4)$

где $\theta$ , $\phi$ $\in \mathbb{R}$ - углы на сфере Блоха, показанные на рис. 1.

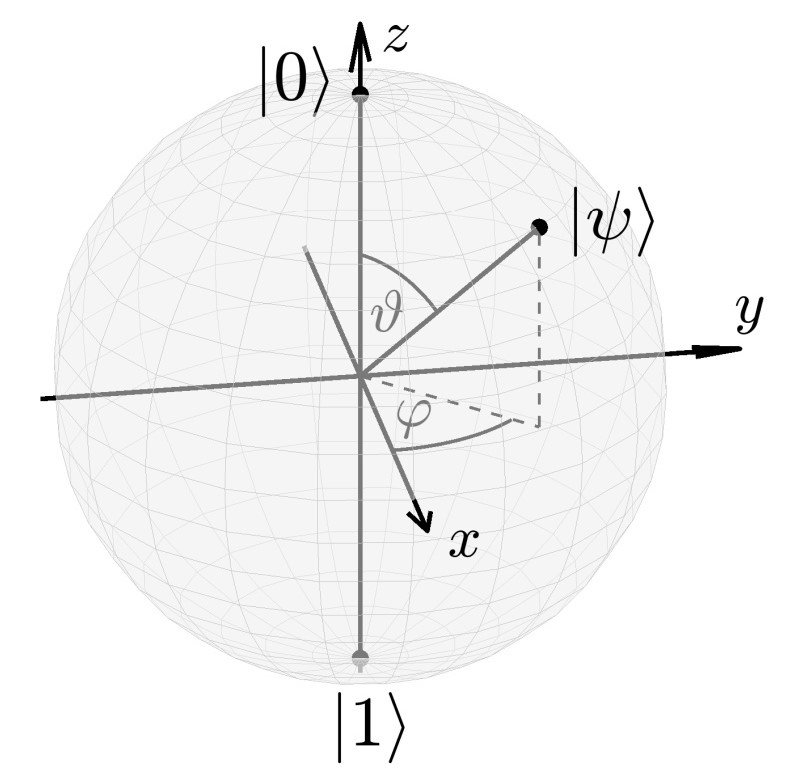
Сфера Блоха является полезной иллюстрацией одиночных кубитов, которая также показывает, как они обобщают классические биты: в то время как классический бит может принимать только два значения, которые представлены на рисунке 1 как Северный полюс $| 0 \rangle$ и Южный полюс $| 1 \rangle$ , кубит может находиться в любом месте сферы Блоха. Таким образом, кубиты имеют значительно больший диапазон возможных значений, что уже дает первый намек на мощь квантовых вычислений. Измерения кубита, однако, могут привести только либо к $| 1 \rangle$ , либо к $| 0 \rangle$ , где точное положение на сфере Блоха определяет соответствующие вероятности. Следовательно, основная задача в квантовых вычислениях состоит в том, чтобы использовать диапазон возможных значений кубита (бесконечно много), даже когда измерения сводят кубит к одному из двух дискретных значений.

Математическое определение кубита, приведённое выше, может принимать различные физические реализации. Для создания кубита в реальном мире подойдет любая квантово-механическая система, которая может принимать одно из двух значений при измерении. Например, кубит может быть реализован с помощью спина электрона. Всякий раз, когда измеряется спин, он будет либо увеличиваться, либо уменьшаться. В промежутках между измерениями вращение развивается в сложной суперпозиции этих двух результатов с коэффициентами, характеризующими вероятности измерений. Существует множество других возможных реализаций кубита. Прелесть квантовых вычислений в том, что они позволяют создать абстрактную теоретическую структуру, основанную на сложных векторах и унитарных матрицах, которая охватывает широкий спектр различных физических реализаций. В некоторой степени это позволяет отделить анализ и разработку квантовых алгоритмов от их физической реализации.

Множество кубитов

Точно так же, как классические компьютеры оперируют многими классическими битами, квантовые компьютеры обычно оперируют несколькими кубитами. В предыдущем разделе мы видели, что кубиты находятся в подмножестве $\mathbb{C}^2$ , которое изоморфно сфере в $\mathbb{R}^3$ . Предположим теперь, что у нас есть таких кубитов $| \psi_{j} \rangle$ , . Квантовое состояние $| \psi \rangle$ , представляющее все кубитов, находится в n-кратном тензорном произведении $\mathbb {C}^2$ на само себя. Точнее, $| \psi \rangle$ – единичный вектор в:

$(\mathbb{C}^2)^{\otimes n} = \underbrace{ \mathbb{C}^2 \otimes ... \otimes \mathbb{C}^2}_{n \ times} = \mathbb{C}^{2^n}. \ (10)$

Составное состояние $| \psi \rangle$ является тензорным произведением $| \psi_j \rangle$ , то есть

Применительно к векторам или матрицам, как в (11), тензорное произведение эквивалентно операции, которая часто используется в теории управления: произведению Кронекера. Принимая тензорные произведения базисных состояний с одним кубитом за $| 0 \rangle$ и $| 1 \rangle$ , базис для $\mathbb{C}^{2^n}$ может быть построен следующим образом:

${|0...000\rangle, \ |0...001\rangle, \ |0...010\rangle, \ ..., \ |1...111\rangle} . \ (12)$

Обратите внимание, что мы используем обозначения, введенные в (11) таким образом, что, например,

Базис (12) обычно называют вычислительным базисом. Например, если и отдельные кубиты принимают форму

$|\psi_1 \rangle = \begin{bmatrix}\alpha_1 \\\beta_1\end{bmatrix}$ и $|\psi_2 \rangle = \begin{bmatrix} \alpha_2 \\ \beta_2 \end{bmatrix}$ ,

тогда составное состояние $|\psi \rangle$ :

$|\psi \rangle = |\psi \rangle \otimes |\psi \rangle = \begin{bmatrix}\alpha_1 \alpha_2 \\\alpha_1 \beta_2 \\\beta_1 \alpha_2 \\\beta_1 \alpha_2\end{bmatrix} = \alpha_1 \alpha_2 |00 \rangle + \alpha_1 \beta_2 |01 \rangle + \beta_1 \alpha_2 |10 \rangle + \beta_1 \beta_2 |11 \rangle . \ (13)$

Интуитивно эта конструкция может быть объяснена с помощью вероятностной интерпретации амплитуд $\alpha_i$ , $\beta_i$ . Если вероятность измерения для состояния $|\psi_1 \rangle$ , соответственно $|\psi_2 \rangle$ , равна $|\alpha_1|^2$ , соответственно $|\alpha_2|^2$ , тогда вероятность измерения 00 для комбинированного состояния $|\psi_2 \rangle \otimes |\psi_2 \rangle$ задается через $|\alpha_1 \alpha_2|^2$ (и аналогично для других возможных результатов измерения 01, 10 и 11).

Состояния $|\psi \rangle$ , которые можно записать в виде $|\psi_1 \rangle \otimes |\psi_2 \rangle$ для каких-то $|\psi_1 \rangle , |\psi_2 \rangle$ , называют сепарабельными. Важно подчеркнуть, что не все состояния являются таковыми, то есть в $\mathbb{C}^{2^n}$ есть единичные векторы, которые не являются сепарабельными, они называются запутанными. Запутанность – загадочное свойство квантовых объектов, описывающее сильную связь между ними, которая не имеет классического аналога. Квантовым вычислениям необходима достаточная степень запутанности для достижения экспоненциального ускорения по сравнению с классическими вычислениями. Давайте в заключение подчеркнем, что размер $\mathbb{C}^{2^n}$ , пространства квантовых состояний, состоящего из кубитов, экспоненциально велик в сравнении с . Это показывает, что, в общем, квантовое состояние может быть представлено на классическом компьютере только для небольшого числа кубитов , то есть для значений таких, что не слишком велико.

Измерения

Как упоминалось выше, получить прямой доступ к значению квантового состояния невозможно. Вместо этого нам нужно провести измерения в соответствии с законами квантовой механики. В этой статье мы для простоты сосредоточимся на проективных измерениях. Проективные измерения всегда выполняются относительно наблюдаемого $\mathcal{M}$ , которое представляет собой эрмитову матрицу размерности (для системы с n кубитами), то есть $\mathcal{M} = \mathcal{M}^\dagger \in \mathbb{C}^{2^n}$ . Согласно спектральной теореме, мы можем записать

$\mathcal{M} = \sum_{i=1}^l \lambda_i P_i, \ (17)$

где $\lambda_i \in R$ – собственные значения $\mathcal{M}$ , а - проекции на соответствующие собственные пространства, то есть, $P_i = v_i v_i^\dagger$ с собственными векторами . Результатом измерения всегда является одно из собственных значений $\lambda_i$ из $\mathcal{M}$ , и вероятность измерения $\lambda_i$ равна

$\langle \psi |P_i| \psi \rangle= \psi^\dagger P_i \psi . \ (18)$

Если результат измерения задается через $\lambda_i$ , то непосредственно после измерения состояние равно

$\psi_{after \ meas.} = \frac {P_i | \psi \rangle} {\sqrt{\langle \psi |P_i| \psi \rangle}} . \ (19)$

Давайте подчеркнем довольно необычный факт: измерение влияет на квантовое состояние $| \psi \rangle$ . Во время измерения $| \psi \rangle$ изменяет свое значение, и через бесконечно малое время после измерения оно становится равным одному из собственных векторов наблюдаемого $\mathcal{M}$ . Этот процесс называется коллапсом квантового состояния $| \psi \rangle$ . Единственная информация, которая извлекается с помощью измерения – это одно из собственных значений $\mathcal{M}$ , которое показывает, на какой собственный вектор свернулось состояние. Тот факт, что измерения влияют на значения квантовых состояний (возможно, нежелательным образом) – это, конечно, плохая новость для управления с обратной связью.

Давайте проиллюстрируем вышеприведённые принципы на примере одного кубита. Наиболее часто рассматриваемой наблюдаемой матрицей является матрица Паули

$Z = \begin{bmatrix} \ 1 & 0\\ \ 0 & -1 \end{bmatrix}$ .

Поскольку собственные векторы являются вычислительным базисом состояний $| 0 \rangle$ и $| 1 \rangle$ , измерения относительно обычно называются измерениями в вычислительном базисе. Чтобы предоставить явные формулы для таких измерений, мы используем спектральную декомпозицию

$Z = \underbrace{1}_{\lambda_1 =} \cdot \underbrace{ \begin{bmatrix}1 & 0\\0 & 0\end{bmatrix}}_{P_1 =} + \underbrace{(-1)}_{\lambda_2 =} \cdot \underbrace{\begin{bmatrix}0 & 0\\0 & 1\end{bmatrix}}_{P_2 =}. \ (20)$

Следовательно, измерение для одного кубита $| \psi \rangle = \alpha | 0 \rangle + \beta | 1 \rangle$ всегда дает одно из собственных значений $\lambda_1 = +1$ или $\lambda_2 = -1$ от . Согласно (18), вероятность измерения $\lambda_1 = +1$ равна:

$\langle \psi |P_i| \psi \rangle = \begin{bmatrix}\alpha\\\beta\end{bmatrix}^\dagger \begin{bmatrix}1 & 0\\0 & 0\end{bmatrix} \begin{bmatrix}\alpha\\\beta\end{bmatrix} = |\alpha|^2, \ (21)$

Объединяя это с (19) если измерение возвращает значение $\lambda_1 = +1$ , то мы можем быть уверены, что кубит находится в состоянии:

$\frac {P_1 | \psi \rangle} {\sqrt{\langle \psi |P_1| \psi \rangle}} = \frac{\begin{bmatrix}1 & 0\\0 & 0\end{bmatrix} \begin{bmatrix}\alpha\\\beta\end{bmatrix}}{\sqrt{|\alpha|^2}} = e^{-\phi_\alpha} | 0 \rangle \ (22)$

с $\phi_\alpha \in \mathbb{R}$ таким , что $e^{-\phi_\alpha} = \frac{\alpha}{|\alpha|}$ . Напомним, что глобальные фазы $|\psi_1 \rangle , |\psi_2 \rangle$ не влияют на результаты измерений (факт, который теперь можно увидеть из (18) и (19) путем умножения $\psi$ на $e^{-\phi_\alpha}$ ). Следовательно, состояние в (22) эквивалентно $| 0 \rangle$ . Подводя итог, можно сказать, что вероятность получения в качестве результата измерения равна $|\alpha|^2$ и если мы измеряем , то состояние сворачивается до $| 0 \rangle$ после измерения. Аналогично, можно показать, что $|\beta|^2$ описывает вероятность измерения , и состояние сворачивается до $| 1 \rangle$ , если измеряется .

Наконец, отметим, что для многих практических целей важно определить полное квантовое состояние, то есть все его коэффициенты в вычислительном базисе (12), а не просто измерение относительно данной наблюдаемой величины. Поскольку кубиты недоступны непосредственно с помощью измерений, для этого были разработаны различные методы под названием квантовой томографии состояний.

Квантовые вентили

Классические компьютеры состоят из набора элементарных логических элементов (например, AND, OR, NOT), которые применяются к строкам классических битов. Аналогично, вычисления на квантовых компьютерах представлены квантовыми элементами, которые применяются к квантовым состояниям. Математически квантовые вентили представляют собой унитарные матрицы $\mathcal{U} \in \mathbb{U}^{2n}$ , то есть элементы $\mathcal{U}$ из $\mathbb{C}^{2n \cdot 2n}$ такие, что $\mathcal{U}^\dagger \mathcal{U} = I$ , где – число кубитов, на которые воздействует $\mathcal{U}$ . Действие элемента $\mathcal{U}$ на состояние $| \psi_{in} \rangle$ задается умножением, то есть,

$| \psi_{out} \rangle = \mathcal{U}| \psi_{in} \rangle. \ (23)$

На рисунке 2 представлена стандартная графическая иллюстрация действия $\mathcal{U}$ на $| \psi_{in} \rangle$ .

Рис 2: Действие на — Рис 2: Действие $\mathcal{U}$ на $| \psi_{in} \rangle$

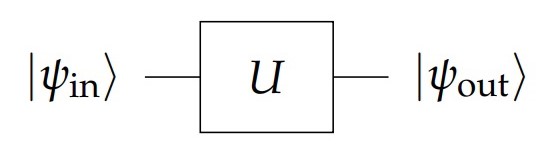
Применение элемента $\mathcal{U}$ к состоянию $| \psi_{in} \rangle$ представляет собой простой пример квантового алгоритма (эквивалентно называемого квантовой схемой). Мы ссылаемся на графическую схему, показанную на рисунке 2, как на схематичное представление элемента $\mathcal{U}$ . По соглашению, квантовые схемы всегда считываются слева направо. Квантовый элемент $\mathcal{U}$ может быть эквивалентно представлен в терминах его эрмитова генератора $H_U = H_U^\dagger$ :

$\mathcal{U} = e^{-iH_U}. \ (24)$

Матрицу обычно называют гамильтоновой из-за ее физического значения.

Унитарность квантовых вентилей имеет несколько интересных следствий. Во-первых, обратите внимание, что квантовые вентили являются линейными операторами, что ограничивает диапазон возможных вычислений на квантовом компьютере. Далее, любой квантовый вентиль $\mathcal{U}$ обратим, причем обратным является его эрмитово сопряженное $\mathcal{U}^\dagger$ . Обратите внимание на фундаментальное отличие от классических вычислений, которое необратимо (рассмотрим элемент AND). Тем не менее, квантовые компьютеры могут выполнять произвольные классические алгоритмы, основанные на элементе Тоффоли (квантовом аналоге элемента NAND) и вспомогательных кубитах. В квантовых вычислениях есть еще несколько интересных явлений, которые связаны с унитарностью квантовых вентилей. Одним из примечательных примеров является теорема о недопустимости клонирования, которая гласит, что скопировать кубиты невозможно, то есть не существует унитарного матричного отображения $|\psi \rangle \otimes | 0 \rangle$ в $|\psi \rangle \otimes |\psi \rangle$ для произвольного $|\psi \rangle$ .

Квантовая криптография

Квантовое распределение ключей (QKD) – это криптографический метод, который позволяет двум сторонам распространять секретный ключ, используя принципы квантовой механики. Протоколы QKD, такие как BB84, QKD на основе приманки и QKD с фазовым дифференциальным сдвигом, были разработаны для обеспечения безопасного распределения ключей. Используя квантовые свойства, такие как принцип неопределенности, QKD позволяет генерировать общий секретный ключ, который невозможно перехватить, не будучи обнаруженным, обеспечивая высокий уровень безопасности криптографических коммуникаций.

Протокол BB84, разработанный Беннеттом и Брассардом в 1984 году, представляет собой протокол квантового распределения ключей (QKD), который использует комбинацию квантового канала и небезопасного классического канала, который необходимо аутентифицировать для распространения секретного ключа между двумя сторонами. Протокол обеспечивает безопасность ключа, обнаруживая любые попытки подслушивания по квантовому каналу, таким образом предоставляя средство обнаружения любых потенциальных нарушений безопасности.

Протокол BB84 использует четыре квантовых состояния, которые случайным образом подготавливаются отправителем, Алисой, в одном из двух базисов (прямолинейный базис или диагональный базис) для передачи информации получателю, Бобу.

В BB84 используются четыре квантовых состояния:

$|0\rangle$ и $|1\rangle$ в прямолинейном базисе (X-базис)
$|+\rangle$ и $|-\rangle$ в диагональном базисе (Z-базис), где $|+\rangle = \frac{1}{\sqrt{2}}(1,1)$ и

$|-\rangle = \frac{1}{\sqrt{2}}(1,-1)$

Принцип работы протокола BB84 изложен ниже на примере с Алисой и Бобом.

На рисунке 3, где показана передача битов между Алисой и Бобом, можно наблюдать, что это в конечном итоге приводит к генерации общего секретного ключа, также известного как просеянный ключ в квантовом распределении ключей (QKD).

Протокол BB84 состоит из следующих шагов:

Алиса генерирует случайную последовательность битов и кодирует каждый бит в случайно выбранное состояние поляризации, используя одно из двух оснований: прямолинейное (R) или диагональное (D).
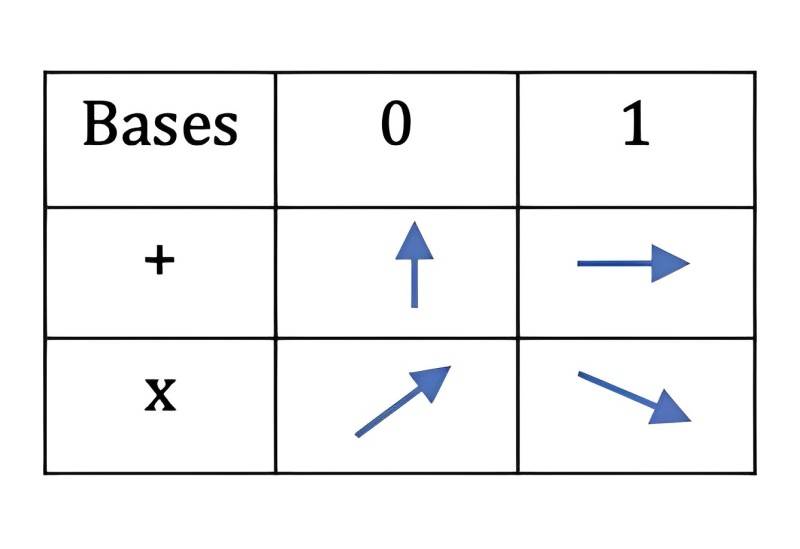
Информация кодируется в неортогональных квантовых состояниях, таких как одиночные фотоны с направлениями поляризации 0, 45, 90 и 135 градусов, в соответствии с рисунком 4.
Алиса отправляет закодированные фотоны Бобу по квантовому каналу.
Боб случайным образом выбирает одно из двух оснований для измерения поляризации каждого фотона, который он получает от Алисы.
Боб измеряет каждый фотон и записывает результаты либо как 0, либо как 1.
После передачи Алиса и Боб публично раскрывают базы, которые они использовали для каждого бита по классическому каналу.
Алиса и Боб отбрасывают биты, в которых базы не совпадали.
Оставшиеся биты образуют просеянный ключ.
Чтобы обеспечить безопасность ключа, Алиса и Боб выполняют тест на обнаружение любого потенциального подслушивания, сравнивая подмножество их просеянного ключа по классическому каналу.
Наконец, они используют методы исправления ошибок и усиления конфиденциальности для извлечения более короткого, но безопасного общего секретного ключа.

Чтобы обеспечить максимальную безопасность ключа, сгенерированного по протоколу BB84, Алиса и Боб тщательно проводят ключевой тест, предназначенный для обнаружения потенциального подслушивания. Он включает в себя сравнение случайно выбранного подмножества их просеянного ключа по классическому каналу. Алиса сообщает выбранное ею подмножество Бобу, который затем сравнивает это со своим собственным подмножеством, делясь результатами с Алисой. Существенная корреляция между подмножествами означает отсутствие подслушивающего устройства на квантовом канале, подтверждая безопасность ключа. И наоборот, отсутствие соответствия указывает на потенциальное прослушивание, что приводит к немедленному завершению протокола. Этот тест, называется этапом "усиления конфиденциальности". Точность и аутентичность ключа зависит от того, проводили ли Алиса и Боб измерения в одних и тех же базах, что приводит к 100 процентной точности, или были выбраны разные базы, что снижает точность до 50 процентов. По сути, протокол BB84 позволяет двум сторонам установить общий секретный ключ по незащищенному каналу, гармонизируя принципы квантовой механики с классической коммуникацией.

Источники:

Комментарии (1)

Jianke
11.01.2024 04:54
#26364162
Круто!