В этом посте я представлю подробный пример математики, используемой внутри модели трансформера, чтобы вы получили хорошее представление о работе модели. Чтобы пост был понятным, я многое упрощу. Мы будем выполнять довольно много вычислений вручную, поэтому снизим размерность модели. Например, вместо эмбеддингов из 512 значений мы используем эмбеддинги из 4 значений. Это позволит упростить понимание вычислений. Мы используем произвольные векторы и матрицы, но при желании вы можете выбрать собственные значения.
Как вы увидите, математика модели не так уж сложна. Сложность возникает из-за количества этапов и количества параметров. Перед прочтением этой статьи я рекомендую прочитать пост Illustrated Transformer (или читать их параллельно) [перевод на Хабре]. Это отличный пост, объясняющий модель трансформера интуитивным (и наглядным!) образом, поэтому я не буду объяснять то, что уже объяснено в нём. Моя цель заключается в том, чтобы объяснить, как работает модель трансформера, а не что это такое. Если вы хотите углубиться в подробности, то изучите известную статью Attention is all you need [перевод на Хабре: первая и вторая части].
Обязательные требования
Для понимания статьи необходимы базовые знания линейной алгебры; в основном мы будем выполнять простые матричные умножения, так что специалистом быть необязательно. Кроме того, будут полезны знания основ машинного обучения и глубокого обучения.
Что рассматривается в статье?
Полный пример математических вычислений, происходящих в модели трансформера в процессе инференса
Объяснение механизмов внимания
Объяснение остаточных связей и нормализации слоёв
Код для масштабирования модели
Наша цель будет заключаться в использовании модели трансформера в качестве инструмента для перевода, чтобы мы могли передать модели входные данные и ожидать от неё генерации перевода. Например, мы можем передать «Hello World» на английском и ожидать на выходе получить «Hola Mundo» на испанском.
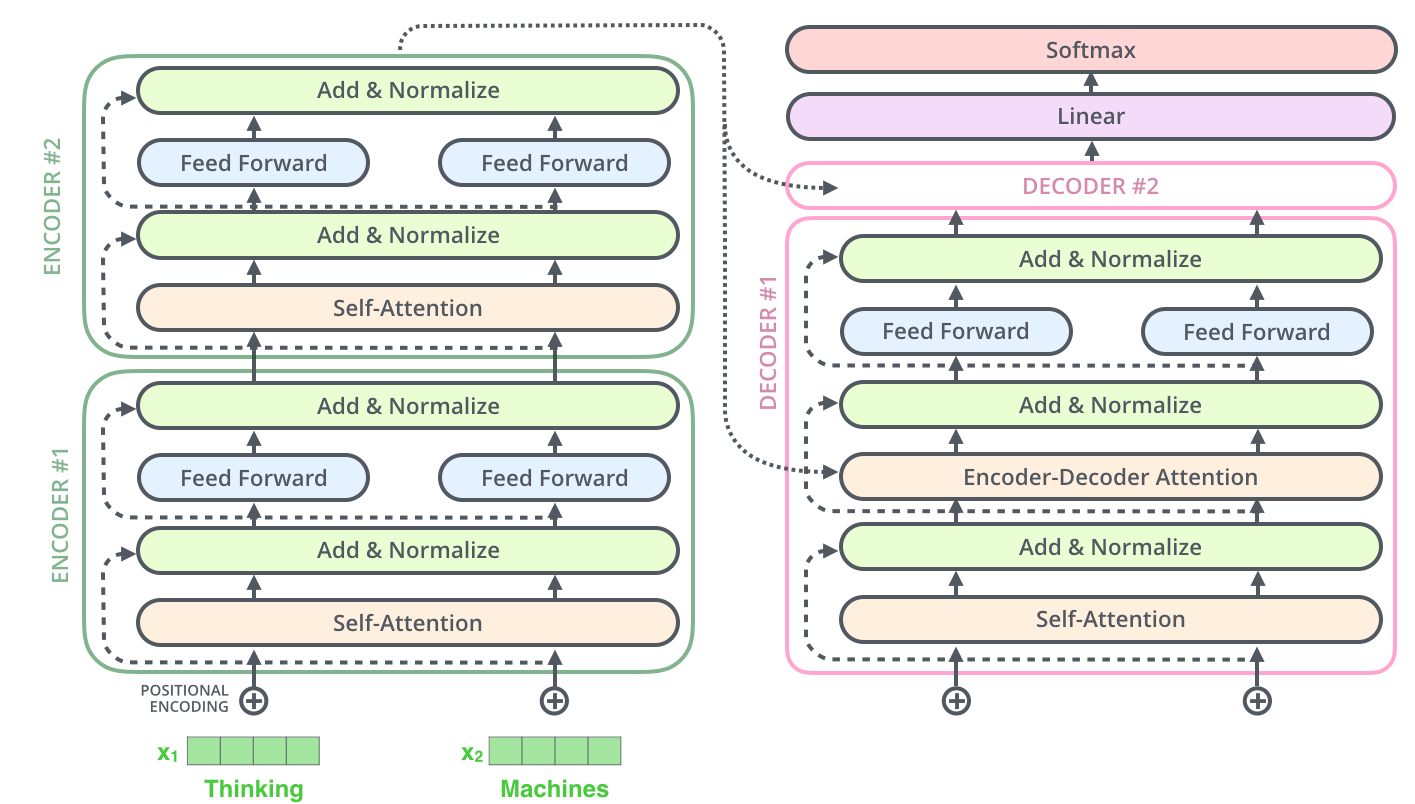
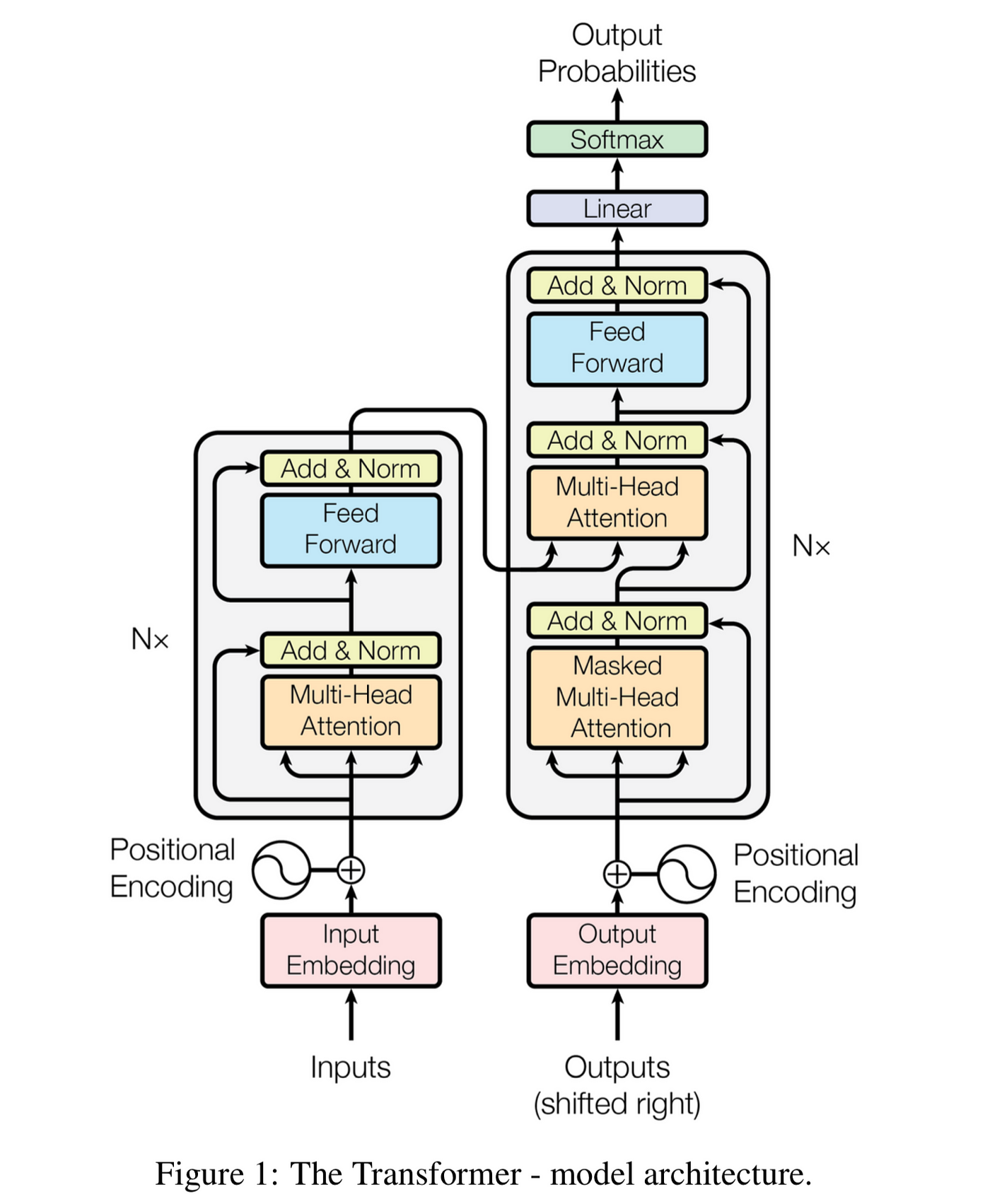
Давайте взглянем на пугающую диаграмму трансформера (не бойтесь, скоро вы её поймёте!):
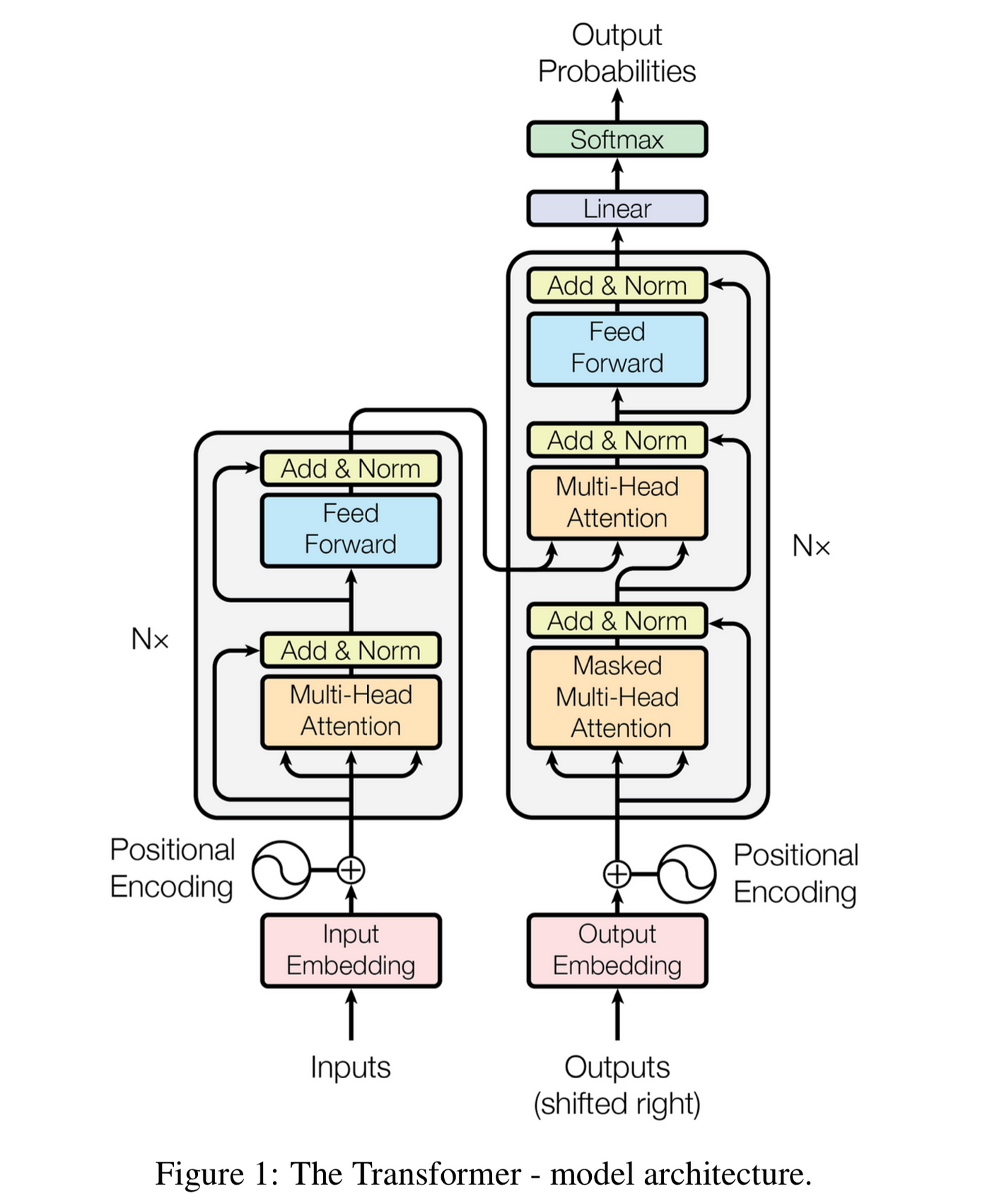
Исходная модель трансформера состоит из двух частей: кодировщика (encoder) и декодера (decoder). Кодировщик занимается «пониманием» или «осознанием смысла» входного текста, а декодер выполняет генерацию выходного текста. Давайте рассмотрим кодировщик.
Кодировщик
Цель работы кодировщика заключается в генерации обогащённого эмбеддингами описания входного текста. Этот эмбеддинг отражает семантическую информацию о входном тексте и передаётся декодеру для генерации выходного текста. Кодировщик состоит из стека из N слоёв. Прежде чем переходить к слоям, нужно разобраться, как передавать слова (или токены) в модель.
Примечание
Термин «эмбеддинг» используется слишком часто. Сначала мы создадим эмбеддинг, который будет входными данными для кодировщика. Кодировщик тоже создаёт на выходе эмбеддинг (иногда называемый hidden states). Декодер тоже получает эмбеддинг! Весь смысл в том, что эмбеддинг описывает токен в виде вектора.
0. Токенизация
Модели машинного обучения могут обрабатывать числа, а не текст, так что нам нужно превратить входной текст в числа. Именно это и выполняет токенизация! Это процесс разбиения входного текста на токены, с каждым из которых связан ID. Например, мы можем разделить текст «Hello World» на два токена: «Hello» и «World». Также мы можем разбить его на символы: «H», «e», «l», «l», «o», « »,«W», «o», «r», «l», «d». Мы сами можем выбирать принцип токенизации, он зависит от данных, с которыми мы работаем.
Для токенизации по словам (разбиения текста на слова) требуется очень большой словарь (всех возможных токенов). В нём слова наподобие «dog» и «dogs» или «run» и «running» будут разными токенами. Словарь символов потребует меньшего объёма, но будет обладать меньшим смыслом (он может быть полезен в языках наподобие китайского, где каждый символ содержит больше информации).
Прогресс двинулся в сторону токенизации по подсловам. Это нечто среднее между токенизацией по словам и по символам. Мы разделяем слова на подслова. Например, слово «tokenization» можно разбить на «token» и «ization». Как принимается решение о месте разбиения слов? Это часть обучения токенизатора при помощи статистического процесса, задача которого заключается в выявлении подслов, которые лучше всего выбрать для конкретного датасета. Это детерминированный процесс (в отличие от обучения модели машинного обучения).
В этой статье я для простоты использую токенизацию по словам. Наша цель будет заключаться в переводе «Hello World» с английского на испанский. Пример «Hello World» мы разобьём на токены «Hello» и «World». Каждому токену присваивается в словаре модели ID. Например, «Hello» может быть токеном 1, а «World» — токеном 2.
1. Эмбеддинг текста
Хотя мы можем передать модели ID токенов (то есть 1 и 2), эти числа не несут никакого смысла. Нужно превратить их в векторы (список чисел). Именно это и выполняет процесс эмбеддинга! Эмбеддинги токена сопоставляют ID токена с вектором фиксированной длины, имеющим семантическое значение токенов. Это создаёт интересные свойства: схожие токены будут иметь схожий эмбеддинг (иными словами, вычисление косинусного коэффициента между двумя эмбеддингами даст нам хорошее понимание степени схожести токенов).
Стоит заметить, что отображение токена в эмбеддинг изучается моделью. Хотя мы можем использовать уже обученный эмбеддинг наподобие word2vec или GloVe, в процессе своего обучения модели трансформеров изучают эти эмбеддинги. Это большое преимущество, поскольку модель может изучить наилучшее описание токенов для поставленной перед ней задачи. Например, модель может научиться тому, что «dog» и «dogs» должны иметь схожие эмбеддинги.
Все эмбеддинги в одной модели имеют одинаковый размер. В трансформере из научной статьи использовался размер 512, но чтобы мы могли выполнять вычисления, снизим его размер до 4. Я назначу каждому токену случайные значения (как говорилось выше, это отображение обычно изучается моделью).
Hello -> [1,2,3,4]
World -> [2,3,4,5]
Примечание
После публикации статьи многие читатели задали вопросы о представленных выше эмбеддингах. Мне было лениво и я просто записал числа, с которыми будет удобно выполнять вычисления. На практике эти числа будут изучаться моделью. Чтобы это было понятнее, я дополнил пост.
Мы можем вычислить схожесть этих векторов при помощи косинусного коэффициента, который для представленных выше векторов будет слишком высоким. На практике вектор, скорее всего, будет выглядеть примерно так: [-0.071, 0.344, -0.12, 0.026, …, -0.008].
Мы можем представить наши входные данные в виде единой матрицы

Примечание
Хотя мы и можем обрабатывать два эмбеддинга как два отдельных вектора, проще работать с ними как с единой матрицей, потому что в дальнейшем мы будем выполнять умножение матриц.
2. Позиционное кодирование
Отдельные эмбеддинги в матрице не содержат информации о позиции слов в предложении, так что нам нужна информация о позиции. Её можно создать, добавив к эмбеддингу позиционное кодирование.
Получить его можно различными способами; мы можем использовать изученный эмбеддинг или фиксированный вектор. В исходной научной статье используется фиксированный вектор, потому что авторы не увидели почти никакой разницы между двумя методиками (см. раздел 3.5 статьи). Мы тоже воспользуемся фиксированным вектором. Функции синуса и косинуса имеют волнообразный паттерн и повторяются. Благодаря использованию этих функций каждая позиция в предложении получает уникальное, но согласованное позиционное кодирование. Их повторяемость поможет модели проще изучать паттерны наподобие близости и расстояния между элементами. В статье используются следующие функции:

Смысл заключается в интерполяции между синусом и косинусом для каждого значения в эмбеддинге (для чётных индексов используется синус, для нечётных используется косинус). Давайте вычислим их для нашего примера!
Для «Hello»
i = 0 (чётный): PE(0,0) = sin(0 / 10000^(0 / 4)) = sin(0) = 0
i = 1 (нечётный): PE(0,1) = cos(0 / 10000^(2*1 / 4)) = cos(0) = 1
i = 2 (чётный): PE(0,2) = sin(0 / 10000^(2*2 / 4)) = sin(0) = 0
i = 3 (нечётный): PE(0,3) = cos(0 / 10000^(2*3 / 4)) = cos(0) = 1
Для «World»
i = 0 (чётный): PE(1,0) = sin(1 / 10000^(0 / 4)) = sin(1 / 10000^0) = sin(1) ≈ 0.84
i = 1 (нечётный): PE(1,1) = cos(1 / 10000^(2*1 / 4)) = cos(1 / 10000^0.5) ≈ cos(0.01) ≈ 0.99
i = 2 (чётный): PE(1,2) = sin(1 / 10000^(2*2 / 4)) = sin(1 / 10000^1) ≈ 0
i = 3 (нечётный): PE(1,3) = cos(1 / 10000^(2*3 / 4)) = cos(1 / 10000^1.5) ≈ 1
В итоге получаем следующее:
«Hello» -> [0, 1, 0, 1]
«World» -> [0.84, 0.99, 0, 1]
Обратите внимание, что эти кодировки имеют ту же размерность, что и исходный эмбеддинг.
Примечание
Мы используем синус и косинус, как и в исходной научной статье, но есть и другие способы реализации. В очень популярном трансформере BERT применяются обучаемые позиционные эмбеддинги.
3. Добавляем позиционное кодирование и эмбеддинг
Теперь мы добавим к эмбеддингу позиционное кодирование. Это выполняется сложением двух векторов.
«Hello» = [1,2,3,4] + [0, 1, 0, 1] = [1, 3, 3, 5]
«World» = [2,3,4,5] + [0.84, 0.99, 0, 1] = [2.84, 3.99, 4, 6]
То есть наша новая матрица, которая будет входными данными для кодировщика, выглядит так:

Если посмотреть на изображение из научной статьи, то можно увидеть, что мы только что выполнили левую нижнюю часть изображения (эмбеддинг + позиционное кодирование).
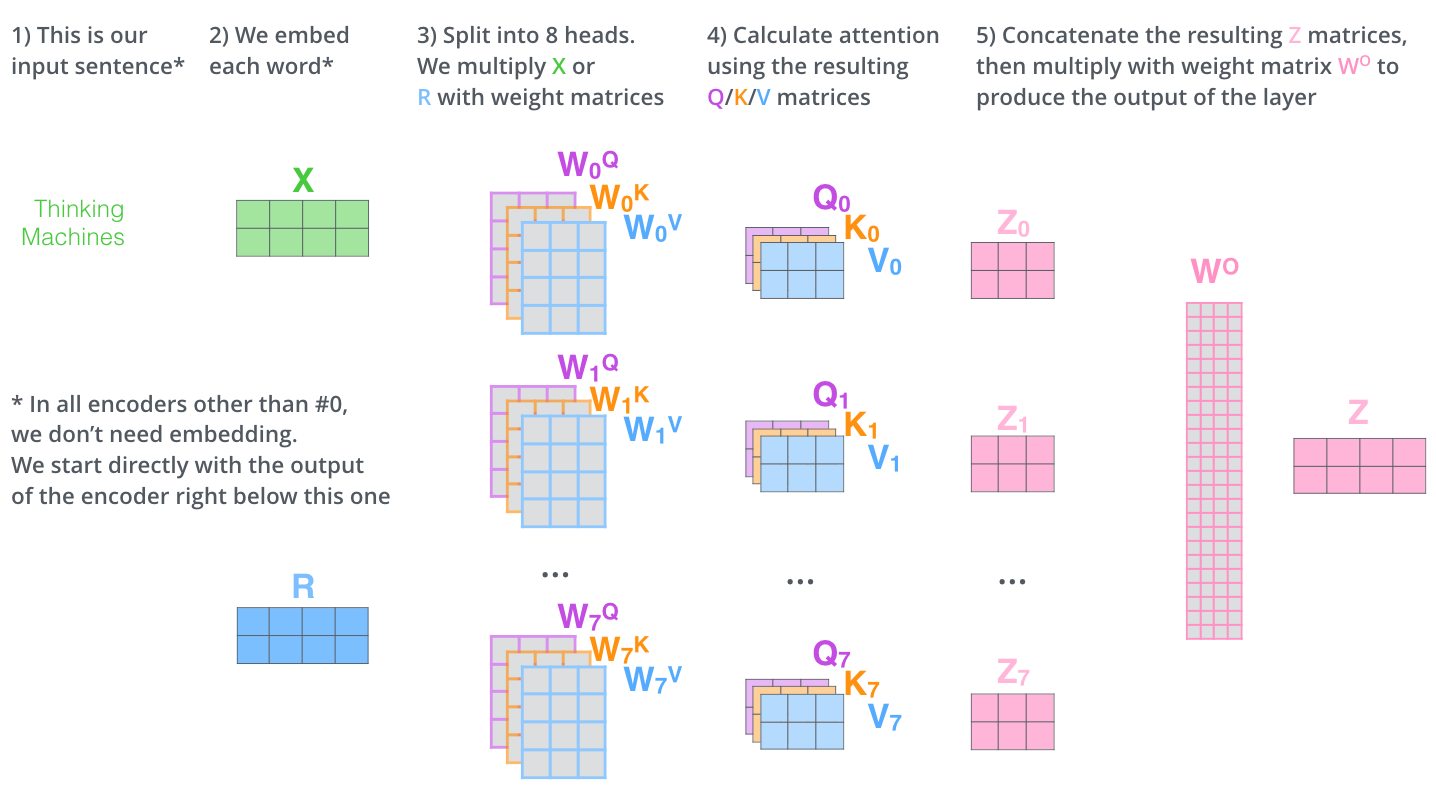
4. Самовнимание
4.1 Определение матриц
Теперь мы введём концепцию многоголового внимания (multi-head attention). Внимание — это механизм, позволяющий модели сосредоточиться на определённых частях входных данных. Многоголовое внимание позволяет модели совместно уделять внимание информации из различных подпространств описаний. Для этого используются множественные головы внимания. Каждая голова внимания имеет собственные матрицы K, V и Q.
Давайте в нашем примере используем две головы внимания. Для этих матриц мы применим случайные значения. Каждая матрица будет иметь размер 4x3. Благодаря этому каждая матрица будет преобразовывать четырёхмерные эмбеддинги в трёхмерные ключи (K), значения (V) и запросы (Q). Это снижает размерность механизма внимания, что помогает управлять вычислительной сложностью. Стоит отметить, что использование слишком малого размера внимания уменьшит точность модели. Давайте используем следующие значения (выбраны произвольно):
Для первой головы

Для второй головы

4.2 Вычисление ключей, запросов и значений
Для получения ключей, запросов и значений нужно умножить входные эмбеддинги на матрицы весов.
Вычисление ключей

На самом деле, нам не нужно вычислять всё это вручную, это будет слишком монотонно. Давайте схитрим и воспользуемся NumPy.
Сначала определим матрицы
import numpy as np
WK1 = np.array([[1, 0, 1], [0, 1, 0], [1, 0, 1], [0, 1, 0]])
WV1 = np.array([[0, 1, 1], [1, 0, 0], [1, 0, 1], [0, 1, 0]])
WQ1 = np.array([[0, 0, 0], [1, 1, 0], [0, 0, 1], [1, 0, 0]])
WK2 = np.array([[0, 1, 1], [1, 0, 1], [1, 1, 0], [0, 1, 0]])
WV2 = np.array([[1, 0, 0], [0, 1, 1], [0, 0, 1], [1, 0, 0]])
WQ2 = np.array([[1, 0, 1], [0, 1, 0], [1, 0, 0], [0, 1, 1]])И убедимся, что в приведённых выше вычислениях нет никаких ошибок.
embedding = np.array([[1, 3, 3, 5], [2.84, 3.99, 4, 6]])
K1 = embedding @ WK1
K1array([[4. , 8. , 4. ],
[6.84, 9.99, 6.84]])Отлично! Теперь давайте получим значения и запросы
Вычисление значений
V1 = embedding @ WV1
V1array([[6. , 6. , 4. ],
[7.99, 8.84, 6.84]])Вычисление запросов
Q1 = embedding @ WQ1
Q1array([[8. , 3. , 3. ],
[9.99, 3.99, 4. ]])Давайте пока пропустим вторую голову и сосредоточимся на окончательном результате первой головы. Ко второй голове мы вернёмся позже.
4.3 Вычисление внимания
Для вычисления показателя внимания требуется пара шагов:
Вычисление скалярного произведения запроса и каждого ключа
Деление результата на квадратный корень размерности вектора ключа
Применение функции softmax для получения весов внимания
Умножение каждого вектора значения на веса внимания
4.3.1 Скалярное произведение запроса и каждого ключа
Для вычисления результата для «Hello» необходимо вычислить скалярное произведение q1 и каждого вектора ключа (k1 и k2)

В мире матриц это будет равно Q1, умноженному на перестановку K1

Я могу сделать ошибку, так что давайте проверим всё это ещё раз с помощью Python
scores1 = Q1 @ K1.T
scores1array([[ 68. , 105.21 ],
[ 87.88 , 135.5517]])4.3.2 Деление на квадратный корень размерности вектора ключа
Затем мы делим показатели на квадратный корень размерности (d) ключей (в данном случае это 3, но в научной статье она была равна 64). Почему? При больших значениях d скалярное произведение растёт слишком быстро (ведь мы складываем умножение кучи чисел, что приводит к большим значениям). А большие значения — это плохо! Подробнее мы поговорим об этом чуть позже.
scores1 = scores1 / np.sqrt(3)
scores1array([[39.2598183 , 60.74302182],
[50.73754166, 78.26081048]])4.3.3 Применение функции softmax
Далее используем softmax для нормализации, чтобы все они были положительны и в сумме равнялись 1.
Что такое softmax?
Softmax — это функция, получающая вектор значений и возвращающая вектор значений между 0 и 1, в котором сумма значений равна 1. Это удобный способ получения вероятностей. Функция определяется следующим образом:

Не пугайтесь этой формулы, на самом деле она довольно проста. Допустим, у нас есть следующий вектор:

Softmax этого вектора будет такой:

Как видите, все значения положительны и в сумме дают 1.
def softmax(x):
return np.exp(x) / np.sum(np.exp(x), axis=1, keepdims=True)
scores1 = softmax(scores1)
scores1array([[4.67695573e-10, 1.00000000e+00],
[1.11377182e-12, 1.00000000e+00]])4.3.4 Умножение матрицы значений на веса внимания
Далее мы умножаем на матрицу значений
attention1 = scores1 @ V1
attention1array([[7.99, 8.84, 6.84],
[7.99, 8.84, 6.84]])Давайте объединим 4.3.1, 4.3.2, 4.3.3 и 4.3.4 в одну формулу с использованием матриц (это из раздела 3.2.1 научной статьи):

Да, вот и всё! Все проделанные нами вычисления можно легко свести к показанной выше формуле внимания! Давайте перенесём это в код.
def attention(x, WQ, WK, WV):
K = x @ WK
V = x @ WV
Q = x @ WQ
scores = Q @ K.T
scores = scores / np.sqrt(3)
scores = softmax(scores)
scores = scores @ V
return scoresattention(embedding, WQ1, WK1, WV1)array([[7.99, 8.84, 6.84],
[7.99, 8.84, 6.84]])Мы убедились, что значения те же, что и получены выше. Давайте воспользуемся этим кодом для получения показателей внимания второй головы внимания:
attention2 = attention(embedding, WQ2, WK2, WV2)
attention2array([[8.84, 3.99, 7.99],
[8.84, 3.99, 7.99]])Если вас интересует, как внимание стало одинаковым для двух эмбеддингов, то это вызвано тем, что softmax переводит показатели в 0 и 1. Смотрите:
softmax(((embedding @ WQ2) @ (embedding @ WK2).T) / np.sqrt(3))array([[1.10613872e-14, 1.00000000e+00],
[4.95934510e-20, 1.00000000e+00]])Это вызвано плохой инициализацией матриц и маленьким размерам векторов. Большие различиях в показателях до применения softmax будут лишь усилены, приводя к том, что одно значение будет близко к 1, а другие к 0. На практике наши исходные значения матрицы эмбеддингов были слишком велики, что привело к высоким значениям для ключей, значений и запросов, которые при умножении становились только выше.
Помните, как мы выполняли деление на квадратный корень размерности ключей? Именно поэтому мы это и делали, в противном случае значения скалярного произведения были бы слишком большими, из-за чего получились бы большие значения после softmax. Однако в данном случае, похоже, этого не было достаточно, учитывая наши небольшие значения! В качестве быстрого хака мы можем уменьшить масштаб значений на меньшее значение, чем квадратный корень трёх. Давайте переопределим функцию внимания, уменьшив масштаб на 30. В долгой перспективе это плохое решение, но оно поможет нам получить разные значения для показателей внимания. Позже мы вернёмся к более качественному решению.
def attention(x, WQ, WK, WV):
K = x @ WK
V = x @ WV
Q = x @ WQ
scores = Q @ K.T
scores = scores / 30 # we just changed this
scores = softmax(scores)
scores = scores @ V
return scoresattention1 = attention(embedding, WQ1, WK1, WV1)
attention1array([[7.54348784, 8.20276657, 6.20276657],
[7.65266185, 8.35857269, 6.35857269]])attention2 = attention(embedding, WQ2, WK2, WV2)
attention2array([[8.45589591, 3.85610456, 7.72085664],
[8.63740591, 3.91937741, 7.84804146]])4.3.5 Выходные значения внимания голов
Следующий слой кодировщика ожидает на входе одну матрицу, а не две. Первым этапом будет конкатенация выходных значений двух голов (см. раздел 3.2.2 научной статьи)
attentions = np.concatenate([attention1, attention2], axis=1)
attentionsarray([[7.54348784, 8.20276657, 6.20276657, 8.45589591, 3.85610456,
7.72085664],
[7.65266185, 8.35857269, 6.35857269, 8.63740591, 3.91937741,
7.84804146]])Затем мы умножаем эту конкатенированную матрицу на матрицу весов, чтобы получить окончательный результат слоя внимания. Этой матрице весов модель тоже обучается! Размерность матрицы гарантирует, что мы вернёмся к той же размерности, что была у эмбеддинга (в нашем случае 4).
# Просто произвольные значения
W = np.array(
[
[0.79445237, 0.1081456, 0.27411536, 0.78394531],
[0.29081936, -0.36187258, -0.32312791, -0.48530339],
[-0.36702934, -0.76471963, -0.88058366, -1.73713022],
[-0.02305587, -0.64315981, -0.68306653, -1.25393866],
[0.29077448, -0.04121674, 0.01509932, 0.13149906],
[0.57451867, -0.08895355, 0.02190485, 0.24535932],
]
)
Z = attentions @ W
Zarray([[ 11.46394285, -13.18016471, -11.59340253, -17.04387829],
[ 11.62608573, -13.47454936, -11.87126395, -17.4926367 ]])Всё это можно объединить в изображение из The Ilustrated Transformer
5. Слой с прямой связью
5.1 Простой слой с прямой связью
После слоя самовнимания у кодировщика идёт нейронная сеть с прямой связью (feed-forward neural network, FFN). Это простая сеть с двумя линейными преобразованиями и активацией ReLU между ними. В посте The Illustrated Transformer подробностей об этом нет, так что я вкратце объясню этот слой. Цель FFN заключается в обработке и трансформировании описания, созданного механизмом внимания. Поток обычно выглядит так (см. раздел 3.3 научной статьи):
Первый линейный слой: обычно он расширяет размерность входных данных. Например, если размерность входных данных равна 512, то размерность выходных данных может быть равна 2048. Это выполняется для того, чтобы позволить модели изучать более сложные функции. В нашем простом примере с размерностью 4 мы расширимся до 8.
Активация ReLU: нелинейная функция активации. Это простая функция, возвращающая 0, если входные данные отрицательны, и входные данные, если они положительны. Это позволяет модели обучаться нелинейным функциям. Вычисления выглядят так:

Второй линейный слой: он противоположен первому линейному слою. Этот слой снова возвращает размерность к исходной. В нашем примере он выполнит снижение с 8 до 4.
Всё это можно описать следующим образом

Напомню, что входными данными для этого слоя является Z, которое мы вычислили в самовнимании. Вот какие значения мы там получили

Теперь давайте зададим произвольные значения для матриц весов и векторов смещений. Я сделаю это в коде, но если у вас хватит терпения, то можете задать их вручную!
W1 = np.random.randn(4, 8)
W2 = np.random.randn(8, 4)
b1 = np.random.randn(8)
b2 = np.random.randn(4)А теперь давайте запишем функцию прямого прохода
def relu(x):
return np.maximum(0, x)
def feed_forward(Z, W1, b1, W2, b2):
return relu(Z.dot(W1) + b1).dot(W2) + b2output_encoder = feed_forward(Z, W1, b1, W2, b2)
output_encoderarray([[ -3.24115016, -9.7901049 , -29.42555675, -19.93135286],
[ -3.40199463, -9.87245924, -30.05715408, -20.05271018]])5.2 Объединяем всё: произвольный кодировщик
Теперь давайте напишем код, чтобы объединить в блоке кодировщика многоголовое внимание и прямую связь.
Примечание
Код оптимизирован для понимания и образовательных целей, а не для производительности, не судите слишком строго!
d_embedding = 4
d_key = d_value = d_query = 3
d_feed_forward = 8
n_attention_heads = 2
def attention(x, WQ, WK, WV):
K = x @ WK
V = x @ WV
Q = x @ WQ
scores = Q @ K.T
scores = scores / np.sqrt(d_key)
scores = softmax(scores)
scores = scores @ V
return scores
def multi_head_attention(x, WQs, WKs, WVs):
attentions = np.concatenate(
[attention(x, WQ, WK, WV) for WQ, WK, WV in zip(WQs, WKs, WVs)], axis=1
)
W = np.random.randn(n_attention_heads * d_value, d_embedding)
return attentions @ W
def feed_forward(Z, W1, b1, W2, b2):
return relu(Z.dot(W1) + b1).dot(W2) + b2
def encoder_block(x, WQs, WKs, WVs, W1, b1, W2, b2):
Z = multi_head_attention(x, WQs, WKs, WVs)
Z = feed_forward(Z, W1, b1, W2, b2)
return Z
def random_encoder_block(x):
WQs = [
np.random.randn(d_embedding, d_query) for _ in range(n_attention_heads)
]
WKs = [
np.random.randn(d_embedding, d_key) for _ in range(n_attention_heads)
]
WVs = [
np.random.randn(d_embedding, d_value) for _ in range(n_attention_heads)
]
W1 = np.random.randn(d_embedding, d_feed_forward)
b1 = np.random.randn(d_feed_forward)
W2 = np.random.randn(d_feed_forward, d_embedding)
b2 = np.random.randn(d_embedding)
return encoder_block(x, WQs, WKs, WVs, W1, b1, W2, b2)Вспомним наши входные данные в матрице E, имеющие позиционное кодирование и эмбеддинг.
embeddingarray([[1. , 3. , 3. , 5. ],
[2.84, 3.99, 4. , 6. ]])Теперь передадим это нашей функции random_encoder_block
random_encoder_block(embedding)array([[ -71.76537515, -131.43316885, 13.2938131 , -4.26831998],
[ -72.04253781, -131.84091347, 13.3385937 , -4.32872015]])Отлично! Это был всего один блок кодировщика. В научной статье применяются шесть кодировщиков. Выходные данные одного кодировщика передаются на следующий и так далее:
def encoder(x, n=6):
for _ in range(n):
x = random_encoder_block(x)
return x
encoder(embedding)/tmp/ipykernel_11906/1045810361.py:2: RuntimeWarning: overflow encountered in exp
return np.exp(x)/np.sum(np.exp(x),axis=1, keepdims=True)
/tmp/ipykernel_11906/1045810361.py:2: RuntimeWarning: invalid value encountered in divide
return np.exp(x)/np.sum(np.exp(x),axis=1, keepdims=True)array([[nan, nan, nan, nan],
[nan, nan, nan, nan]])5.3 Остаточные связи и нормализация слоёв
Ой-ёй! У нас начали появляться NaN! Похоже, наши значения слишком велики и при передаче следующему кодировщику они оказываются слишком большими и «взрываются»! Эта проблема слишком больших значений часто возникает при обучении моделей. Например, когда мы выполняем обратное распространение ошибки (методику, при помощи которой модели обучаются), градиенты могут оказаться слишком большими и в результате «взрываются»; это называется взрывом градиентов (gradient explosion). Без нормализации небольшие изменения во входных данных на первых слоях в последующих слоях усиливаются. Это распространённая проблема в глубоких нейросетях. Существует два способа борьбы с этой проблемой: остаточные связи и нормализация слоёв (они вкратце упоминаются в разделе 3.1 научной статьи).
Остаточные связи просто прибавляют входные данные слоя к его выходным данным. Например, мы складываем исходный эмбеддинг с выходными данными внимания. Остаточные связи устраняют проблему исчезающих градиентов. Логика в том, что если градиент слишком мал, то мы можем просто сложить входные данные к выходным, и градиент станет больше. Вычисления очень просты:

Вот и всё! Мы сделаем это для выходных данных внимания и выходных данных слоя с прямой связью.
Нормализация слоя — это методика нормализации входных данных слоя. Она выполняет нормализацию по размерности эмбеддинга. Логика в том, что мы хотим нормализовать входные значения слоя, чтобы они имели среднее значение 0 и квадратическое отклонение 1. Это помогает с градиентным потоком. Вычисления на первый взгляд выглядят не так уж просто.

Давайте объясним каждый параметр:
μ — это среднее значение эмбеддинга
σ — это квадратическое отклонение эмбеддинга
ε — это малое число, чтобы избежать деления на ноль. В случае нулевого значения квадратичного отклонения этот маленький эпсилон спасает нас.
γ и β — это изучаемые параметры, управляющие этапами масштабирования и сдвига.
В отличие от пакетной нормализации (batch normalization, не волнуйтесь, если не знаете, что это такое), нормализация слоёв нормализует по размерности эмбеддинга; это означает, что на каждый эмбеддинг не будут влиять другие сэмплы в пакете. Идея заключается в том, что мы хотим нормализовать входные данные слоя, чтобы они имели среднее значение 0 и квадратичное отклонение 1.
Зачем мы добавляем изучаемые параметры γ и β? Причина в том, что мы не хотим терять силу представления слоя. Если просто нормализовать входные данные, то какая-то информация может потеряться. Добавляя изучаемые параметры, мы можем научиться масштабировать и сдвигать нормализованные значения.
Соединив эти уравнения, мы получим уравнение для всего кодировщика:

Давайте проверим его на нашем примере! Возьмём прежние значения E и Z:

Теперь давайте вычислим нормализацию слоя; можно разделить этот процесс на три этапа:
Вычисление среднего и дисперсии для каждого эмбеддинга.
Нормализация вычитанием среднего в своей строке и делением на квадратный корень дисперсии строки (плюс малое число, чтобы избежать деления на ноль).
Масштабирование и сдвиг умножением на гамму и прибавлением беты.
5.3.1 Среднее и дисперсия
Для первого эмбеддинга

То же самое можно сделать для второго эмбеддинга. Пропустим сами вычисления и покажем только результат.

Давайте проверим при помощи Python
(embedding + Z).mean(axis=-1, keepdims=True)array([[-4.58837567],
[-3.59559107]])(embedding + Z).std(axis=-1, keepdims=True)array([[ 9.92061529],
[10.50653019]])Отлично! Теперь нормализуем
5.3.2 Нормализация
При нормализации из каждого значения в эмбеддинге мы вычитаем среднее и делим его на квадратичное отклонение. Эпсилон — это очень маленькое значение, например, 0,00001. Чтобы упростить, будем считать, что γ = 1, а β = 0.

Для второго эмбеддинга мы не будем выполнять вычисления вручную. Проверим их при помощи кода. Переопределим функцию encoder_block, внеся следующее изменение:
def layer_norm(x, epsilon=1e-6):
mean = x.mean(axis=-1, keepdims=True)
std = x.std(axis=-1, keepdims=True)
return (x - mean) / (std + epsilon)
def encoder_block(x, WQs, WKs, WVs, W1, b1, W2, b2):
Z = multi_head_attention(x, WQs, WKs, WVs)
Z = layer_norm(Z + x)
output = feed_forward(Z, W1, b1, W2, b2)
return layer_norm(output + Z)layer_norm(Z + embedding)array([[ 1.71887693, -0.56365339, -0.40370747, -0.75151608],
[ 1.71909039, -0.56050453, -0.40695381, -0.75163205]])Сработало! Давайте ещё раз попробуем пропустить эмбеддинг через шесть кодировщиков.
def encoder(x, n=6):
for _ in range(n):
x = random_encoder_block(x)
return x
encoder(embedding)array([[-0.335849 , -1.44504571, 1.21698183, 0.56391289],
[-0.33583947, -1.44504861, 1.21698606, 0.56390202]])Отлично! Значения приемлемые и отсутствуют NaN! Идея стека кодировщиков заключается в том, что на выходе они выдают непрерывное описание z, передающее смысл входной последовательности. Затем это описание передаётся декодеру, который генерирует выходную последовательность символов по одному элементу за раз.
Прежде чем приступать к декодеру, взглянем на изображение из потрясающего поста Джея:
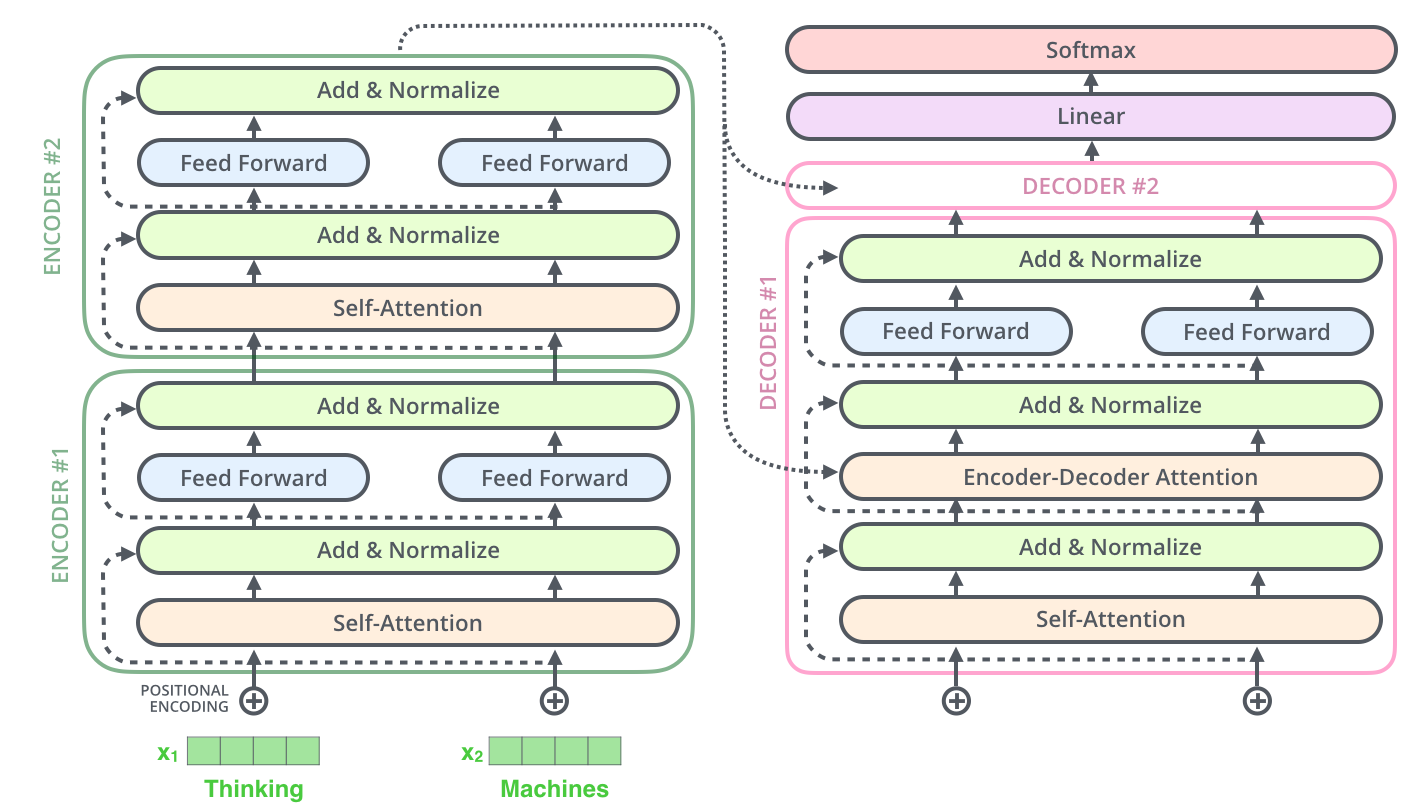
Каждый из элементов в левой части должен быть вам уже понятен! Впечатляет, правда? А теперь давайте перейдём к декодеру.
Декодер
Большинство знаний, полученных при изучении кодировщиков, будет использоваться и в декодере! Декодер имеет два слоя самовнимания, один для кодировщика, другой для декодера. Также декодер имеет слой с прямой связью. Давайте разберём каждую из частей по порядку.
Блок декодера получает два элемента входных данных: выходные данные кодировщика и сгенерированную выходную последовательность. Выходные данные кодировщика — это описание входной последовательности. В процессе инференса сгенерированная выходная последовательность начинается с особого токена начала последовательности (start-of-sequence token, SOS). Во время обучения целевая выходная последовательность — это действительная выходная последовательность, сдвинутая на одну позицию. Скоро это станет вам понятнее!
Имея сгенерированный кодировщиком эмбеддинг и токен SOS, декодер генерирует следующий токен последовательности, то есть «hola». Декодер авторегрессивен, то есть он берёт ранее сгенерированные токены и снова генерирует второй токен.
Итерация 1: входные данные — SOS, выходные — «hola»
Итерация 2: входные данные — SOS + «hola», выходные — «mundo»
Итерация 3: входные данные — SOS + «hola» + «mundo», выходные — EOS
Здесь SOS — это токен начала последовательности, а EOS — токен конца последовательности. После генерации токена EOS декодер прекращает работу. Он генерирует по одному токену за раз. Обратите внимание, что во всех итерациях используется эмбеддинг, сгенерированный кодировщиком.
Примечание
Такая авторегрессивная структура замедляет работу декодера. Кодировщик способен генерировать свой эмбеддинг за один прямой проход, а декодеру необходимо выполнить множество прямых проходов. Это одна из причин, по которым архитектуры, использующие один кодировщик (например, BERT или модели схожести предложений) гораздо быстрее, чем архитектуры с одними только декодерами (например, GPT-2 или BART).
Давайте разберём каждый из этапов! Как и кодировщик, декодер состоит из стека блоков декодеров. Блок декодера чуть сложнее, чем блок кодировщика. Его общая структура такова:
Слой самовнимания (маскированный)
Остаточная связь и нормализация слоя
Слой внимания кодировщика-декодера
Остаточная связь и нормализация слоя
Слой с прямой связью
Остаточная связь и нормализация слоя
Мы уже знакомы со всей математикой пунктов 1, 2, 3, 5 и 6. Взглянув на правую часть изображения ниже, вы увидите, что все эти блоки вам уже известны :
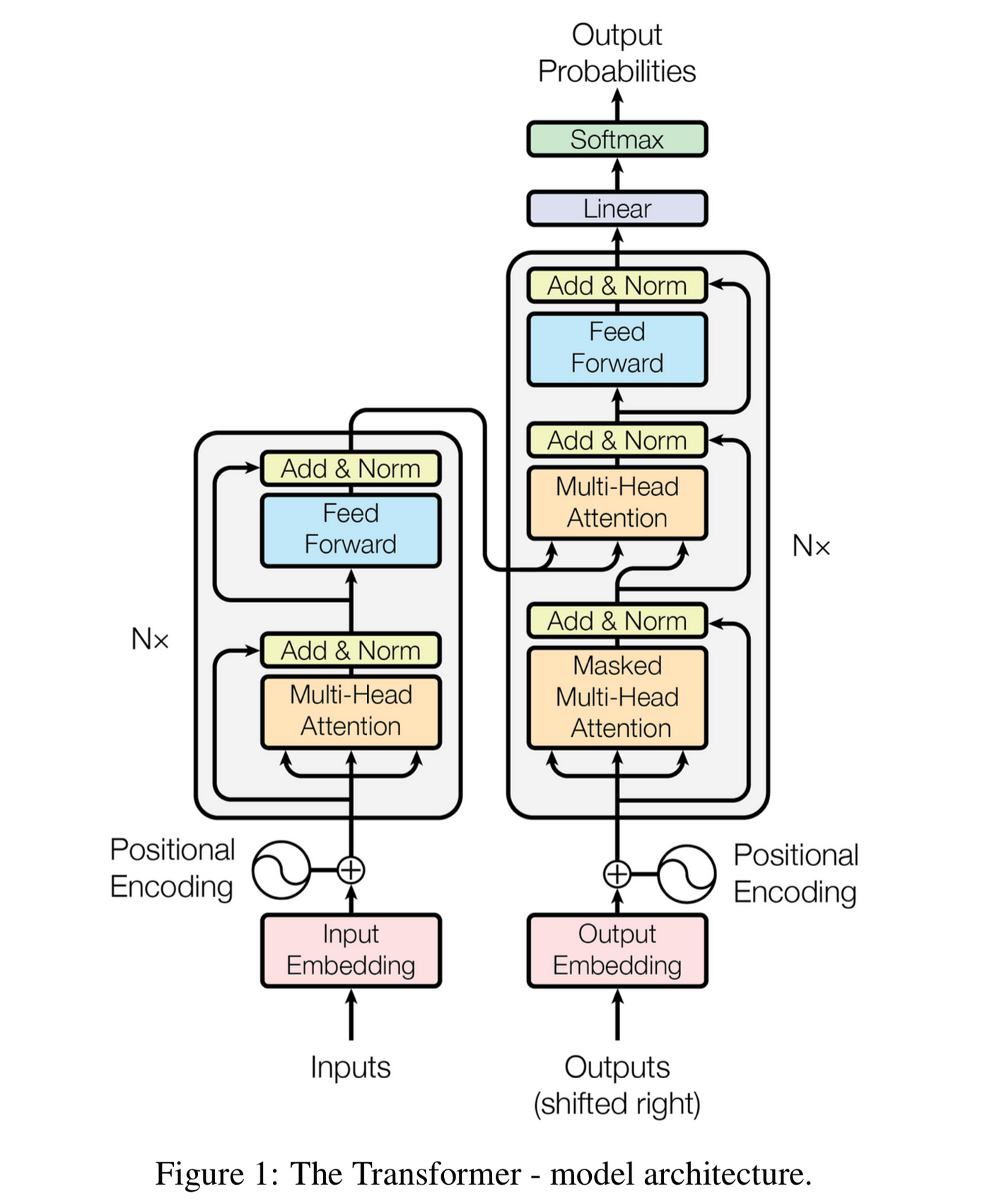
1. Эмбеддинг текста
Первый текст декодера нужен для эмбеддинга входных токенов. Входным токеном является SOS, так что мы выполняем его эмбеддинг. Используется та же размерность эмбеддинга, что и для кодировщика. Предположим, вектор эмбеддинга для SOS имеет такой вид:

2. Позиционное кодирование
Теперь мы добавим в эмбеддинг позиционное кодирование, как делали это в случае с кодировщиком. Учитывая, что это так же позиция, что и у «Hello», у нас будет то же позиционное кодирование, что и раньше:
i = 0 (чётный): PE(0,0) = sin(0 / 10000^(0 / 4)) = sin(0) = 0
i = 1 (нечётный): PE(0,1) = cos(0 / 10000^(2*1 / 4)) = cos(0) = 1
i = 2 (чётный): PE(0,2) = sin(0 / 10000^(2*2 / 4)) = sin(0) = 0
i = 3 (нечётный): PE(0,3) = cos(0 / 10000^(2*3 / 4)) = cos(0) = 1
3. Сложение позиционного кодирования и эмбеддинга
Сложение позиционного кодирования с эмбеддингом выполняется сложением двух векторов:

4. Самовнимание
Первый этап в блоке декодера — это механизм самовнимания. К счастью, у нас есть для этого код и мы можем просто его использовать!
d_embedding = 4
n_attention_heads = 2
E = np.array([[1, 1, 0, 1]])
WQs = [np.random.randn(d_embedding, d_query) for _ in range(n_attention_heads)]
WKs = [np.random.randn(d_embedding, d_key) for _ in range(n_attention_heads)]
WVs = [np.random.randn(d_embedding, d_value) for _ in range(n_attention_heads)]
Z_self_attention = multi_head_attention(E, WQs, WKs, WVs)
Z_self_attentionarray([[ 2.19334924, 10.61851198, -4.50089666, -2.76366551]])Примечание
С точки зрения инференса всё довольно просто, однако с точки зрения обучения есть сложности. При обучении мы используем неразмеченные данные: просто кучу текстовых данных, которые собираем частым скрейпингом в вебе. Цель кодировщика — передача всей информации входных данных, а задача декодера —предсказание следующего наиболее вероятного токена. Это значит, что декодер может использовать только ранее сгенерированные токены (он не может схитрить и посмотреть следующие токены).
Из-за этого мы используем маскированное самовнимание: маскируем ещё не сгенерированные токены. Это выполняется присвоением показателям внимания значений -inf. Так делается в научной статье (раздел 3.2.3.1). Пока мы это пропустим, но важно помнить, что при обучении декодер чуть сложнее.
5. Остаточные связи и нормализация слоёв
Здесь нет ничего таинственного, мы просто складываем входные данные с выходными данными самовнимания и применяем нормализацию слоя. Используется тот же код, что и выше.
Z_self_attention = layer_norm(Z_self_attention + E)
Z_self_attentionarray([[ 0.17236212, 1.54684892, -1.0828824 , -0.63632864]])6. Внимание кодировщика-декодера
Эта часть новая! Если вы задавались вопросом, куда направляются генерируемые кодировщиком эмбеддинги, то сейчас самое время для них!
Предположим, что выходными данными кодировщика является такая матрица:

В механизме самовнимания мы вычисляем запросы, ключи и значения для входного эмбеддинга.
Во внимании кодировщика-декодера мы вычисляем запросы из предыдущего слоя декодера и ключи и значения из выходных данных кодировщика! Все вычисления остаются такими же, что и раньше; единственное отличие в том, какой эмбеддинг использовать для запросов. Давайте взглянем на код
def encoder_decoder_attention(encoder_output, attention_input, WQ, WK, WV):
# В следующих трёх строках и состоит основное различие!
K = encoder_output @ WK # Обратите внимание, что теперь мы передаём предыдущие выходные данные кодировщика!
V = encoder_output @ WV # Обратите внимание, что теперь мы передаём предыдущие выходные данные кодировщика!
Q = attention_input @ WQ # То же, что и для самовнимания
# Остаётся таким же
scores = Q @ K.T
scores = scores / np.sqrt(d_key)
scores = softmax(scores)
scores = scores @ V
return scores
def multi_head_encoder_decoder_attention(
encoder_output, attention_input, WQs, WKs, WVs
):
# Обратите внимание, что теперь мы передаём предыдущие выходные данные кодировщика!
attentions = np.concatenate(
[
encoder_decoder_attention(
encoder_output, attention_input, WQ, WK, WV
)
for WQ, WK, WV in zip(WQs, WKs, WVs)
],
axis=1,
)
W = np.random.randn(n_attention_heads * d_value, d_embedding)
return attentions @ WWQs = [np.random.randn(d_embedding, d_query) for _ in range(n_attention_heads)]
WKs = [np.random.randn(d_embedding, d_key) for _ in range(n_attention_heads)]
WVs = [np.random.randn(d_embedding, d_value) for _ in range(n_attention_heads)]
encoder_output = np.array([[-1.5, 1.0, -0.8, 1.5], [1.0, -1.0, -0.5, 1.0]])
Z_encoder_decoder = multi_head_encoder_decoder_attention(
encoder_output, Z_self_attention, WQs, WKs, WVs
)
Z_encoder_decoderarray([[ 1.57651431, 4.92489307, -0.08644448, -0.46776051]])Сработало! Возможно, вы зададитесь вопросом: «зачем мы это делаем?». Дело в том, что мы хотим, чтобы декодер сосредоточился на релевантных частях входного текста (то есть «hello world»). Внимание кодировщика-декодера позволяет каждой позиции в декодере посетить все позиции входной последовательности. Это очень полезно для таких задач, как перевод, когда декодеру нужно сосредоточиться на релевантных частях входной последовательности. Декодер будет учиться сосредотачиваться на релевантных частях входной последовательности, учась генерировать правильные выходные токены. Это очень мощный механизм!
7. Остаточные связи и нормализация слоя
Всё то же, что и раньше!
Z_encoder_decoder = layer_norm(Z_encoder_decoder + Z_self_attention)
Z_encoder_decoderarray([[-0.44406723, 1.6552893 , -0.19984632, -1.01137575]])8. Слой с прямой связью
И тут то же самое! После этого я также выполню остаточную связь и нормализацию слоя.
W1 = np.random.randn(4, 8)
W2 = np.random.randn(8, 4)
b1 = np.random.randn(8)
b2 = np.random.randn(4)
output = layer_norm(feed_forward(Z_encoder_decoder, W1, b1, W2, b2) + Z_encoder_decoder)
outputarray([[-0.97650182, 0.81470137, -2.79122044, -3.39192873]])9. Объединяем всё: произвольный декодер
Давайте напишем код для одного блока декодера. Самое главное изменение заключается в том, что теперь у нас есть дополнительный механизм внимания.
d_embedding = 4
d_key = d_value = d_query = 3
d_feed_forward = 8
n_attention_heads = 2
encoder_output = np.array([[-1.5, 1.0, -0.8, 1.5], [1.0, -1.0, -0.5, 1.0]])
def decoder_block(
x,
encoder_output,
WQs_self_attention, WKs_self_attention, WVs_self_attention,
WQs_ed_attention, WKs_ed_attention, WVs_ed_attention,
W1, b1, W2, b2,
):
# То же, что и раньше
Z = multi_head_attention(
x, WQs_self_attention, WKs_self_attention, WVs_self_attention
)
Z = layer_norm(Z + x)
# Основное различие заключается в следующих трёх строках!
Z_encoder_decoder = multi_head_encoder_decoder_attention(
encoder_output, Z, WQs_ed_attention, WKs_ed_attention, WVs_ed_attention
)
Z_encoder_decoder = layer_norm(Z_encoder_decoder + Z)
# То же, что и раньше
output = feed_forward(Z_encoder_decoder, W1, b1, W2, b2)
return layer_norm(output + Z_encoder_decoder)
def random_decoder_block(x, encoder_output):
# Просто несколько произвольных инициализаций
WQs_self_attention = [
np.random.randn(d_embedding, d_query) for _ in range(n_attention_heads)
]
WKs_self_attention = [
np.random.randn(d_embedding, d_key) for _ in range(n_attention_heads)
]
WVs_self_attention = [
np.random.randn(d_embedding, d_value) for _ in range(n_attention_heads)
]
WQs_ed_attention = [
np.random.randn(d_embedding, d_query) for _ in range(n_attention_heads)
]
WKs_ed_attention = [
np.random.randn(d_embedding, d_key) for _ in range(n_attention_heads)
]
WVs_ed_attention = [
np.random.randn(d_embedding, d_value) for _ in range(n_attention_heads)
]
W1 = np.random.randn(d_embedding, d_feed_forward)
b1 = np.random.randn(d_feed_forward)
W2 = np.random.randn(d_feed_forward, d_embedding)
b2 = np.random.randn(d_embedding)
return decoder_block(
x, encoder_output,
WQs_self_attention, WKs_self_attention, WVs_self_attention,
WQs_ed_attention, WKs_ed_attention, WVs_ed_attention,
W1, b1, W2, b2,
)def decoder(x, decoder_embedding, n=6):
for _ in range(n):
x = random_decoder_block(x, decoder_embedding)
return x
decoder(E, encoder_output)array([[ 0.25919176, 1.49913566, -1.14331487, -0.61501256],
[ 0.25956188, 1.49896896, -1.14336934, -0.61516151]])Генерация выходной последовательности
У нас уже есть все необходимые части! Давайте сгенерируем выходную последовательность.
У нас есть кодировщик, получающий входную последовательность и генерирующий его обогащённое описание. Он состоит из стека блоков кодировщиков.
У нас есть декодер, получающий выходные данные кодировщика и сгенерированные токены и генерирующий выходную последовательность. Он состоит из стека блоков декодеров.
Как перейти от выходных данных декодера к слову? Нужно добавить поверх декодера последний линейный слой и слой softmax. Весь алгоритм в целом выглядит так:
Обработка кодировщиком: кодировщик получает входную последовательность и генерирует контекстуализированное описание всего предложения при помощи стека блоков кодировщиков.
Инициализация декодера: процесс декодирования начинается с эмбеддинга токена SOS (Start of Sequence), соединённого с выходными данными кодировщика.
Работа декодера: декодер использует выходные данные кодировщика и эмбеддинги всех ранее сгенерированных токенов для создания нового списка эмбеддингов.
Линейный слой для логитов: линейный слой применяется к последнему выходному эмбеддингу декодера для генерации логитов, представляющих сырые предсказания следующего токена.
Softmax для вероятностей: затем эти логиты передаются через слой softmax, преобразующий их в распределение вероятностей по потенциальным следующим токенам.
Итеративная генерация токенов: этот процесс повторяется, и на каждом этапе декодер генерирует следующий токен на основании кумулятивных эмбеддингов ранее сгенерированных токенов и исходных выходных данных кодировщика.
Формирование предложения: эти этапы генерации продолжаются, пока не будет создан токен EOS (End of Sequence) или не достигнута заранее заданная максимальная длина предложения.
Об этом говорится в разделе 3.4 научной статьи.
1. Линейный слой
Линейный слой — это простое линейное преобразование. Он получает выходные данные декодера и преобразует их в вектор размера vocab_size. Это размер словаря. Например, если у нас есть словарь из 10000 слов, то линейный слой преобразовал бы выходные данные декодера в вектор размера 10000. Этот вектор содержал бы вероятность того, что каждое слово будет следующим словом в последовательности. Для простоты можно начать со словаря из 10 слов и предположить, что первые выходные данные декодера — это очень простой вектор: [1, 0, 1, 0]. Мы используем произвольные веса и матрицы перекосов размера vocab_size x decoder_output_size.
def linear(x, W, b):
return np.dot(x, W) + b
x = linear([1, 0, 1, 0], np.random.randn(4, 10), np.random.randn(10))
xarray([ 0.06900542, -1.81351091, -1.3122958 , -0.33197364, 2.54767851,
-1.55188231, 0.82907169, 0.85910931, -0.32982856, -1.26792439])Примечание
Что используется в качестве входных данных для линейного слоя? Декодер будет выводить по одному эмбеддингу для каждого токена в последовательности. Входными данными для линейного слоя станет последний сгенерированный эмбеддинг. Последний эмбеддинг включает в себя информацию для всей последовательности до этого этапа, то есть содержит всю информацию, необходимую для генерации следующего токена. Это значит, что каждый выходной эмбеддинг декодера содержит информацию о всей последовательности до этого этапа.
2. Softmax
Они называются логитами, но интерпретировать их не так просто. Для получения вероятностей можно применить функцию softmax.
softmax(x)array([[0.01602618, 0.06261303, 0.38162024, 0.03087794, 0.0102383 ,
0.00446011, 0.01777314, 0.00068275, 0.46780959, 0.00789871]])И так мы получили вероятности! Предположим, словарь имеет такой вид:

Мы видим, что вероятности таковы:
hello: 0.01602618
mundo: 0.06261303
world: 0.38162024
how: 0.03087794
?: 0.0102383
EOS: 0.00446011
SOS: 0.01777314
a: 0.00068275
hola: 0.46780959
c: 0.00789871
Из этого видно, что наиболее вероятный следующий токен — это «hola». Если всегда выбирается наиболее вероятный токен, это называется жадным декодингом. Это не всегда наилучший подход, потому что он может привести к субоптимальным результатам, но пока мы не будем сейчас углубляться в методики генерации. Если хотите узнать о них подробнее, то прочитайте потрясающий пост.
3. Случайный трансформер из кодировщика и декодера
Давайте напишем код целиком. Зададим словарь, сопоставляющий слова с их изначальными эмбеддингами. Надо отменить, что это тоже изучается при обучении, но пока мы используем случайные значения.
vocabulary = [
"hello",
"mundo",
"world",
"how",
"?",
"EOS",
"SOS",
"a",
"hola",
"c",
]
embedding_reps = np.random.randn(10, 4)
vocabulary_embeddings = {
word: embedding_reps[i] for i, word in enumerate(vocabulary)
}
vocabulary_embeddings{'hello': array([-0.32106406, 2.09332588, -0.77994069, 0.92639774]),
'mundo': array([-0.59563791, -0.63389256, 1.70663692, -0.99495115]),
'world': array([ 1.35581862, -0.0323546 , 2.76696887, 0.83069982]),
'how': array([-0.52975474, 0.94439644, 0.80073818, -1.50135518]),
'?': array([-0.88116833, 0.13995055, 2.01827674, -0.52554391]),
'EOS': array([1.12207024, 1.40905796, 1.22231714, 0.02267638]),
'SOS': array([-0.60624082, -0.67560165, 0.77152125, 0.63472247]),
'a': array([ 1.67622229, -0.20319309, -0.18324905, -0.24258774]),
'hola': array([ 1.07809402, -0.83846408, -0.33448976, 0.28995976]),
'c': array([ 0.65643157, 0.24935726, -0.80839751, -1.87156293])}А теперь напишем произвольный метод generate , авторегрессивно генерирующий токены.
def generate(input_sequence, max_iters=3):
# Сначала мы кодируем входные данные в эмбеддинги
# Для простоты мы пропустим этап позиционного кодирования
embedded_inputs = [
vocabulary_embeddings[token] for token in input_sequence
]
print("Embedding representation (encoder input)", embedded_inputs)
# Затем генерируем описание эмбеддинга
encoder_output = encoder(embedded_inputs)
print("Embedding generated by encoder (encoder output)", encoder_output)
# Инициализируем выходные данные декодера эмбеддингом начального токена
sequence_embeddings = [vocabulary_embeddings["SOS"]]
output = "SOS"
# Случайные матрицы для линейного слоя
W_linear = np.random.randn(d_embedding, len(vocabulary))
b_linear = np.random.randn(len(vocabulary))
# Мы ограничиваем количество этапов декодинга, чтобы избежать слишком последовательностей без EOS
for i in range(max_iters):
# Этап декодера
decoder_output = decoder(sequence_embeddings, encoder_output)
# Используем для предсказания только последние выходные данные
logits = linear(decoder_output[-1], W_linear, b_linear)
# Обёртываем логиты в список, потому что softmax нужны пакеты/2D-массив
probs = softmax([logits])
# Получаем наиболее вероятный следующий токен
next_token = vocabulary[np.argmax(probs)]
sequence_embeddings.append(vocabulary_embeddings[next_token])
output += " " + next_token
print(
"Iteration", i,
"next token", next_token,
"with probability of", np.max(probs),
)
# Если следующий токен последний, то возвращаем последовательность
if next_token == "EOS":
return output
return output, sequence_embeddingsДавайте запустим код!
generate(["hello", "world"])Embedding representation (encoder input) [array([-0.32106406, 2.09332588, -0.77994069, 0.92639774]), array([ 1.35581862, -0.0323546 , 2.76696887, 0.83069982])]
Embedding generated by encoder (encoder output) [[ 1.14747807 -1.5941759 0.36847675 0.07822107]
[ 1.14747705 -1.59417696 0.36847441 0.07822551]]
Iteration 0 next token hola with probability of 0.4327111653266739
Iteration 1 next token mundo with probability of 0.4411354383451089
Iteration 2 next token world with probability of 0.4746898792307499('SOS hola mundo world',
[array([-0.60624082, -0.67560165, 0.77152125, 0.63472247]),
array([ 1.07809402, -0.83846408, -0.33448976, 0.28995976]),
array([-0.59563791, -0.63389256, 1.70663692, -0.99495115]),
array([ 1.35581862, -0.0323546 , 2.76696887, 0.83069982])])Отлично, теперь у нас есть токены «how», «a» и «c». Это неправильный перевод, но этого вполне можно было ожидать, ведь веса мы использовали случайные.
Советую ещё раз подробно изучить всю архитектуру кодировщика-декодера из научной статьи:
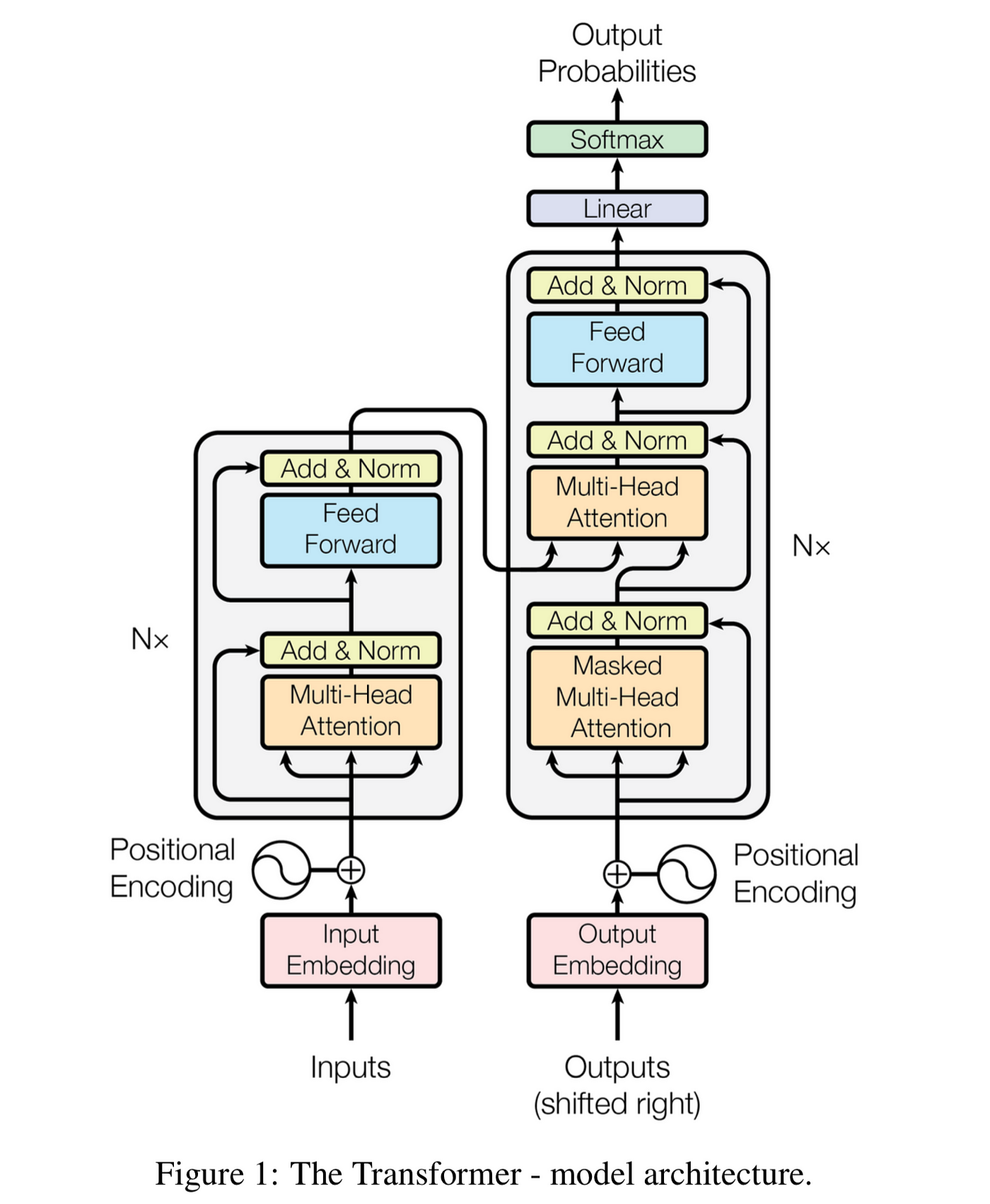
Заключение
Надеюсь, пост показался вам интересным и информативным! Мы рассмотрели множество аспектов. Но разве это всё? На самом деле, практически да! В архитектуры новых трансформеров добавляют множество трюков, но фундамент трансформера именно таков, каким мы его описали. В зависимости от задачи также можно использовать только кодировщик или декодер. Например, в задачах, требующих понимания, например, в классификации, можно использовать стек кодировщиков с линейным слоем поверх него. Для задач, требующих генерации, например, в переводе, можно использовать стеки кодировщиков и декодеров. А для свободной генерации, например, как в ChatGPT или Mistral, можно применять только стек декодеров.
Разумеется, мы многое упростили. Давайте вкратце проверим, какие были числа в научной статье о трансформере:
Размерность эмбеддингов: 512 (в нашем примере 4)
Количество кодировщиков: 6 (в нашем примере 6)
Количество декодеров: 6 (в нашем примере 6)
Размерность прямой связи: 2048 (в нашем примере 8)
Количество голов внимания: 8 (в нашем примере 2)
Размерность внимания: 64 (в нашем примере 3)
Мы рассмотрели множество тем, но довольно интересно, то мы можем достичь впечатляющих результатов, увеличив масштабы этих вычислений и проведя умное обучение. Мы не рассмотрели в посте обучение, потому что наша цель заключалась в понимании вычислений при использовании готовой модели, но я надеюсь, что это станет надёжным фундаментом для перехода к обучению!
Также можно найти более формальный документ с вычислениями в этом PDF.
Упражнения
Вот несколько упражнений, чтобы попрактиковаться в понимании трансформера.
В чём предназначение позиционного кодирования?
Чем отличаются самовнимание и внимание кодировщика-декодера?
Что произойдёт, если размерность внимания слишком мала? А если слишком велика?
Вкратце опишите структуру слоя с прямой связью.
Почему декодер медленнее кодировщика?
Какова цель остаточных связей и нормализации слоёв?
Как выполняется переход от выходных данных декодера к вероятностям?
Почему выбор каждый раз самого вероятного следующего токена может вызвать проблемы?
Ресурсы
The Illustrated Transformer [перевод на Хабре]
Attention is all you need [перевод на Хабре: первая и вторая части]


johnfound
Статья, нужная. Но я с самого начала не понял что это эмбединг, зачем он нужен и как он из токенов получается. И понятное дело, вся остальная статья потом звучала как на китайском.
В переводе ли дело, или статья и так неясная была изначально трудно сказать. Но мне кажется, что второе.
Firsto
Это так называемые векторы слов для определения контекстного сходства.
То есть слова, которые регулярно встречаются рядом в тексте, также будут находиться в непосредственной близости в векторном пространстве.
P.S.: Статья сложная, согласен, ещё бы все предыдущие осилить, на которые тут ссылаются.)