Архитектура

TOY - это минималистичный воображаемый процессор (хотя были попытки его воплощения в реальность). Его описал профессор Phil Koopman в своей статье Microcoded Versus Hard-wired Control ещё в 1987 году. TOY изучают на парах по Computer Science в Принстонском университете.

Я взял слайды используемые на занятиях и разложил всё по полочкам.

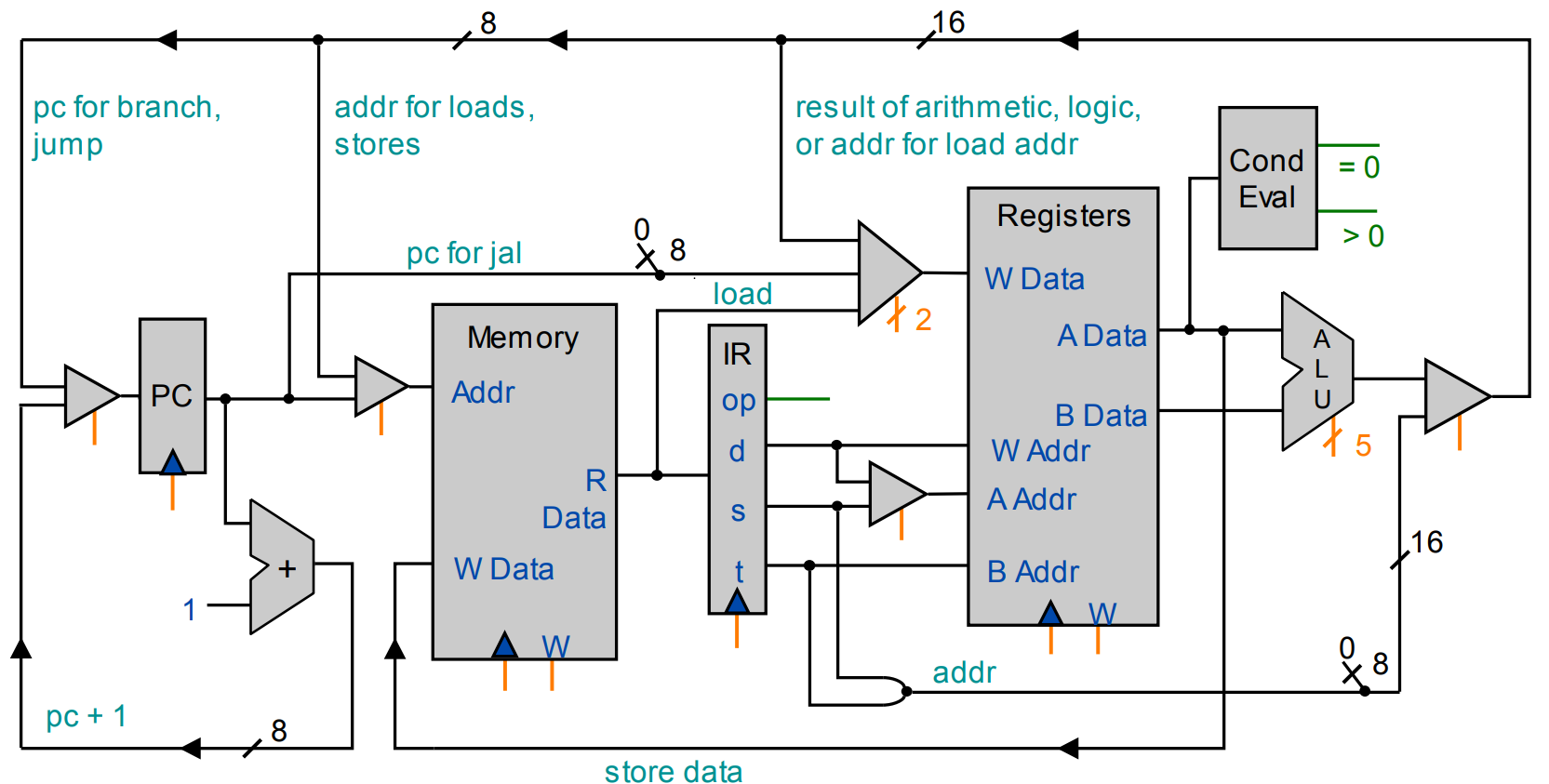
Основные особенности:

• арифметическо-логическое устройство

• 16 16-битных регистров

• 256 16-битных слов памяти и устройство ввода-вывода

• один 8-битный счётчик команд

• 16 инструкций

Не густо. Как где-то сказали: "Машина Тьюринга на минималках". Давайте приступим и напишем простой скелет эмулятора на Python:

class Toy:
	def __init__(self):
        self.registers = self.Registers()
        self.memory = self.Memory()
        self.alu = self.ALU()
        self.pc = 0x10

Сделаем для начала наиболее простую реализацию.

Регистры и память

В TOY 16 регистров по 16 бит и 256 ячеек памяти по 16 бит. Они доступны для чтения и записи. Поэтому выделим каждому по массиву данных и назначим простейшие функции чтения и записи:

class Registers:
    __REGISTERS_NUM = 16
    
    def __init__(self):
        self.image = [0 for i in range(self.__REGISTERS_NUM)]

    def read(self, addr):
        return self.image[addr]

    def write(self, addr, data):
        self.image[addr] = data

class Memory:
    __MEMORY_SIZE = 255
    
    def __init__(self):
        self.image = [0 for i in range(self.__MEMORY_SIZE)]

    def read(self, addr):
        return self.image[addr]

    def write(self, addr, data):
        self.image[addr] = data

Счётчик команд

Счётчик инструкций или program counter - это специальный регистр процессора, который указывает на следующую инструкцию в программе, которую надо исполнить. Программа состоит из инструкций лежащих в памяти. С помощью этого счётчика компьютер проходит вдоль всего кода попутно извлекая и исполняя эти инструкции.

В TOY программа начинается с адреса 16 (0x10):

class Toy:
	def __init__(self):
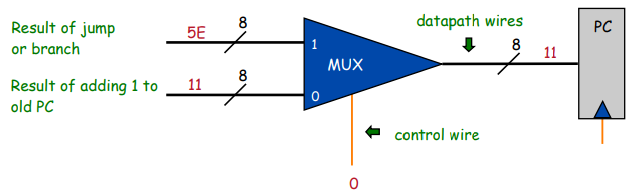
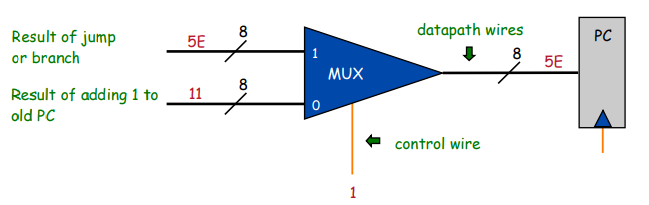
        self.pc = 0x10

При исполнении обычных инструкций он будет увеличиваться на единицу, а в операциях типа "Jump" будет сдвигаться сразу на несколько шагов вперёд или назад:

Архитектура набора команд (Instruction Set Architecture)

Основное отличие одного ядра процессора от другого - это набор команд (opcode), который они могут выполнить.

Инструкция TOY состоит из 16 бит в двух форматах:

То есть при извлечении инструкции из памяти (instruction fetch) нам нужно получить параметры этих форматов:

def fetch(self):
    instruction = self.memory.read(self.pc)
    opcode = (instruction & 0xF000) >> 12
    d      = (instruction & 0x0F00) >> 8
    s      = (instruction & 0x00F0) >> 4
    t      = (instruction & 0x000F)
    addr   = (instruction & 0x00FF)
    self.pc = self.pc + 1
    return opcode, d, s, t, addr

TOY может выполнять всего 16 команд (операций):

Чувствуете этот запах? Так пахнут бессонные ночи, красные глаза и его величество... Ассемблер!

Здесь всего 16 команд. Например, даже в 50-летнем Intel 4004 их было 52, а в x86 вообще 1502. Но даже этих 16-ти команд достаточно для ЛЮБОГО вычисления. Ограничивает только размер памяти.

Пропишем функции этих операций.

def op_halt(self, d, s, t, addr):
    print('HALT')
    exit()

def op_add(self, d, s, t, addr): # R[d] = R[s] + R[t]
    self.registers.write(d, self.registers.read(s) + self.registers.read(t))

def op_sub(self, d, s, t, addr): # R[d] = R[s] - R[t]
    self.registers.write(d, self.registers.read(s) - self.registers.read(t))
    
def op_and(self, d, s, t, addr): # R[d] = R[s] & R[t]
    self.registers.write(d, self.registers.read(s) & self.registers.read(t))
    
def op_xor(self, d, s, t, addr): # R[d] = R[s] ^ R[t]
    self.registers.write(d, self.registers.read(s) ^ self.registers.read(t))
    
def op_shl(self, d, s, t, addr): # R[d] = R[s] << R[t]
    self.registers.write(d, self.registers.read(s) << self.registers.read(t))
    
def op_shr(self, d, s, t, addr): # R[d] = R[s] >> R[t]
    self.registers.write(d, self.registers.read(s) >> self.registers.read(t))
    
def op_loada(self, d, s, t, addr): # R[d] = addr
    self.registers.write(d, addr)
    
def op_load(self, d, s, t, addr): # R[d] = M[addr]
    self.registers.write(d, self.memory.read(addr))
    
def op_stor(self, d, s, t, addr): # M[addr] = R[d]
    self.memory.write(addr, self.registers.read(d))
    
def op_loadi(self, d, s, t, addr): # R[d] = M[R[t]]
    self.registers.write(d, self.registers.read(t))
    
def op_stori(self, d, s, t, addr): # M[R[t]] = R[d]
    self.memory.write(self.registers.read(t), self.registers.read(d))
    
def op_bzero(self, d, s, t, addr): # if (R[d] == 0) PC = addr
    if self.registers.read(d) == 0:
        self.pc = addr
    
def op_bposi(self, d, s, t, addr): # if (R[d] > 0) PC = addr
    if self.registers.read(d) > 0:
        self.pc = addr
    
def op_jmpr(self, d, s, t, addr): # PC = R[d]
    self.pc = self.registers.read(d)
    
def op_jmpl(self, d, s, t, addr): # R[d] = PC + 1; PC = addr
    self.registers.write(d, self.pc)
    self.pc = addr

И пропишем эти функции в таблицу в соответствии с кодами команд:

execute = {
    0x0: op_halt,
    0x1: op_add,
    0x2: op_sub,
    0x3: op_and,
    0x4: op_xor,
    0x5: op_shl,
    0x6: op_shr,
    0x7: op_loada,
    0x8: op_load,
    0x9: op_stor,
    0xA: op_loadi,
    0xB: op_stori,
    0xC: op_bzero,
    0xD: op_bposi,
    0xE: op_jmpr,
    0xF: op_jmpl
}

Теперь работа TOY (как и работа любого компьютера) будет выглядеть всего лишь так:

def start(self):
    while True:
        op, d, s, t, addr = self.fetch()
        self.execute[op](self, d, s, t, addr)

Т.е. по сути компьютер просто производит бесконечное извлечение инструкций из памяти (fetch) и их выполнение (execute).

Загрузка программы

Напишем простую программу сложения и посмотрим на состояние регистров. Добавим отладку регистров:

def start(self):
    while True:
        op, d, s, t, addr = self.fetch()
        execute[op](self, d, s, t, addr)
        
        # debug registers
        print("Regs: ", self.registers.image)

Запишем несколько инструкций в память и запустим эмулятор:

computer = Toy()
computer.memory.write(0x10, 0x7328) # R[3] = 40
computer.memory.write(0x11, 0x7464) # R[4] = 100
computer.memory.write(0x12, 0x1234) # R[2] = R[3] + R[4]
computer.start()

Первая инструкция расположена по адресу 0x10, т.к. при старте счётчик команд начинает считать с этого адреса. Запускаем:

# python toy.py
Regs:  [0, 0, 0, 40, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Regs:  [0, 0, 0, 40, 100, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Regs:  [0, 0, 140, 40, 100, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
HALT

Оно работает!

Углубляемся

Поздравляем, завелось! Но как-то всё быстро получилось... Предлагаю на этом простейшем каркасе докопаться до самых транзисторов. Начнём с АЛУ.

АЛУ

Вместо выполнения арифметических операций силами Python, добавим АЛУ. Оно здесь умеет только прибавлять, отнимать, сдвигать биты и выполнять AND и XOR. "Это вам не Рио-де-Жанейро", никаких вам делений с плавающей точкой за одну инструкцию.

Рассмотрим суммирование двух чисел. Любая логическая схема состоит из простейших логический элементов:

Для построения схемы суммирования нам понадобится полусумматор:

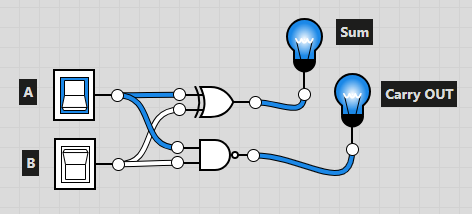
Или выражаясь в коде:

half_adder = lambda a, b: (a ^ b, a & b)

Из двух полусумматоров необходимо собрать полный сумматор:

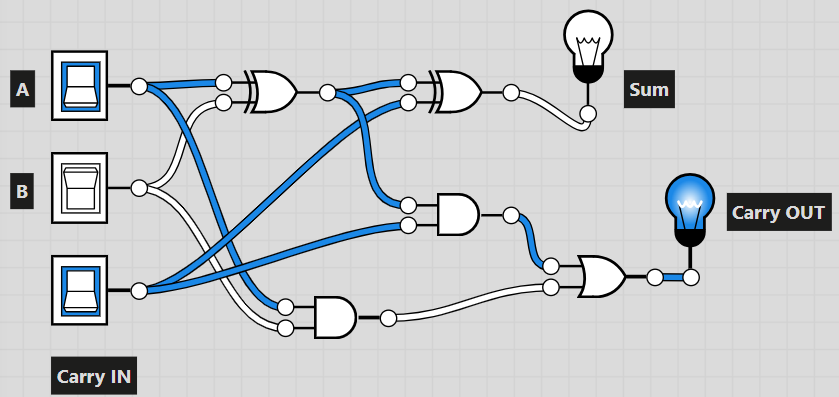
Или:

def full_adder(self, a, b, carry_in):
    half_adder = lambda a, b: (a ^ b, a & b)
    s1, c1 = half_adder(a, b)
    sum, c2 = half_adder(carry_in, s1)
    return sum, c1 | c2

Если посмотреть на схему АЛУ, то можно увидеть, что между операцией сложения и вычитания практически нет разницы:

Нужно всего лишь ввести дополнительную переменную substract для полного сумматора, и он превратится в сумматор-вычитатель:

def adder_substractor(self, a, b, carry_in, substract):
	return self.full_adder(a, b ^ substract, carry_in)

Доведём схему до 16 бит:

def adder_substractor(self, input1, input2, substract):
  result_byte = 0
  carry = substract
  bit_from_byte = lambda byte, position: (byte & (1 << position)) >> position
  for position in range(self.DATA_RESOLUTION):
      bit1 = bit_from_byte(input1, position)
      bit2 = bit_from_byte(input2, position)
      result_bit, carry = self.full_adder(bit1, bit2 ^ carry, carry)
      result_byte |= (result_bit << position)
  return result_byte

В общем принцип понятен, не будем заморачиваться с остальными операциями.

class ALU:
    __DATA_RESOLUTION = 16
    __CTRL_ADD_SUB	= 0b000
    __CTRL_AND		= 0b001
    __CTRL_XOR		= 0b010
    __CTRL_SHIFT	= 0b011
    __CTRL_INPUT2	= 0b100

    __SUBSTRACT_RESET = 0b0
    __SUBSTRACT_SET   = 0b1

    __SHIFT_RIGHT = 0b0
    __SHIFT_LEFT  = 0b1

    def __full_adder(self, a, b, carry_in):
        half_adder = lambda a, b: (a ^ b, a & b)
        s1, c1 = half_adder(a, b)
        sum, c2 = half_adder(carry_in, s1)
        return sum, c1 | c2

    def __adder_substractor(self, a, b, cr, sub):
        return self.__full_adder(a, b ^ sub, cr)
    
    def __alu(self, input1, input2, substract, shift_dir, ctrl):
        result_byte = 0
        if ctrl == self.__CTRL_ADD_SUB:
            carry = substract
            bit_from_byte = lambda byte, position: (byte & (1 << position)) >> position
            for position in range(self.__DATA_RESOLUTION):
                bit1 = bit_from_byte(input1, position)
                bit2 = bit_from_byte(input2, position)
                result_bit, carry = self.__adder_substractor(bit1, bit2, carry, substract)
                result_byte |= (result_bit << position)
        elif ctrl == self.__CTRL_AND:
            result_byte = input1 & input2
        elif ctrl == self.__CTRL_XOR:
            result_byte = input1 ^ input2
        elif ctrl == self.__CTRL_SHIFT:
            if shift_dir == self.__SHIFT_LEFT:
                result_byte = input1 << (input2 & 0b1111) # 16 steps max, only 4 bits in use
            else:
                result_byte = input1 >> (input2 & 0b1111) # 16 steps max, only 4 bits in use
        elif ctrl == self.__CTRL_INPUT2:
            result_byte = input2

        return result_byte

    def Add(self, input1, input2):
        return self.__alu(input1, input2, self.__SUBSTRACT_RESET, self.__SHIFT_RIGHT, self.__CTRL_ADD_SUB)

    def Sub(self, input1, input2):
        return self.__alu(input1, input2, self.__SUBSTRACT_SET,   self.__SHIFT_RIGHT, self.__CTRL_ADD_SUB)

    def And(self, input1, input2):
        return self.__alu(input1, input2, self.__SUBSTRACT_RESET, self.__SHIFT_RIGHT, self.__CTRL_AND)

    def Xor(self, input1, input2):
        return self.__alu(input1, input2, self.__SUBSTRACT_RESET, self.__SHIFT_RIGHT, self.__CTRL_XOR)

    def Shiftl(self, input1, input2):
        return self.__alu(input1, input2, self.__SUBSTRACT_RESET, self.__SHIFT_LEFT,  self.__CTRL_SHIFT)

    def Shiftr(self, input1, input2):
        return self.__alu(input1, input2, self.__SUBSTRACT_RESET, self.__SHIFT_RIGHT, self.__CTRL_SHIFT)
    
    def Input2(self, input1, input2):
        return self.__alu(input1, input2, self.__SUBSTRACT_RESET, self.__SHIFT_RIGHT, self.__CTRL_INPUT2)

Ещё раз про регистры

Поскольку компьютер - это по сути электрическая схема, то за одну операцию можно и читать значения регистров и тут же записать вычисленное значение. Посмотрим, как это происходит на основе уже созданной программы:

computer.memory.write(0x10, 0x7328) # R[3] = 40
computer.memory.write(0x11, 0x7464) # R[4] = 100
computer.memory.write(0x12, 0x1234) # R[2] = R[3] + R[4]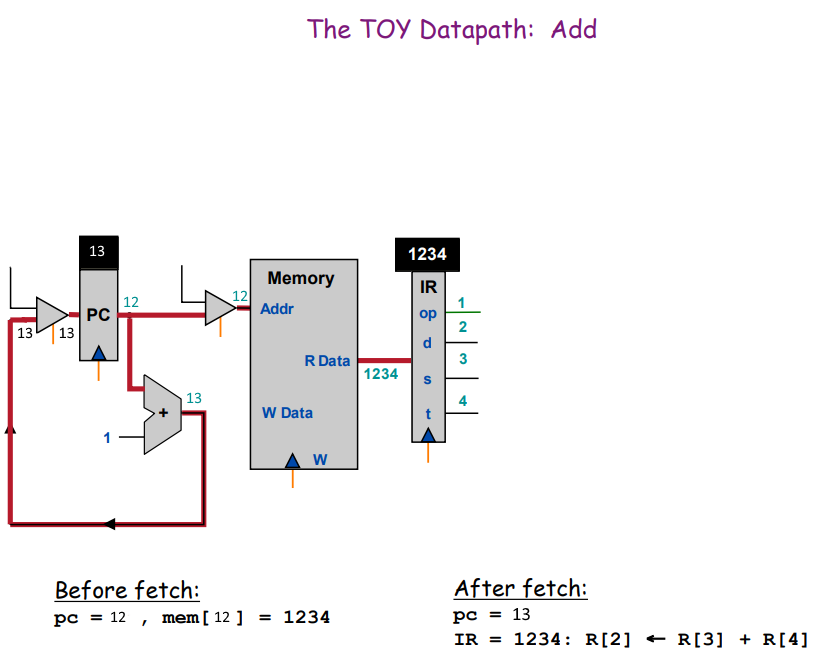

До извлечения инструкции по адресу 0x12 в регистр 3 записано значение 0x28, а в 4 - 0x64. Инструкция извлекается из памяти и распарсевается на op, d, s и t. Переходим к исполнению инструкции:

На входящие шины A Addr и B Addr попадают значения 3 и 4. Значения регистров 3 и 4 отдаются в АЛУ по шинам A Data и B Data, которые сразу же складываются. Полученное значение отправляется на шину W Data регистров по адресу на шине W Addr. И всё это за один такт!

def op_add(self, d, s, t, addr): # R[d] = R[s] + R[t]
    a_data, b_data = self.registers.read(s, t)
    w_data = self.alu.Add(a_data, b_data)
    self.registers.write(w_data, d)

def op_sub(self, d, s, t, addr): # R[d] = R[s] - R[t]
    a_data, b_data = self.registers.read(s, t)
    w_data = self.alu.Sub(a_data, b_data)
    self.registers.write(w_data, d)

...

Что касается самого принципа запоминания. Простейшая ячейка памяти (ОЗУ, регистр или счётчик) состоит из элементов NAND замкнутых друг на друга. Эффект запоминания как раз и строится на этой замкнутости: состояние выхода зависит от того, каким было предыдущее состояние системы:

Память и устройство ввода-вывода

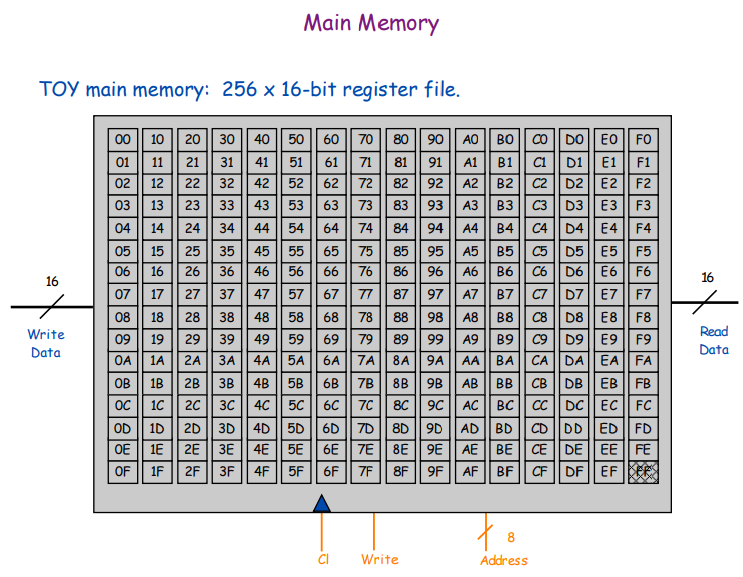
Устройство ввода-вывода замаплено в адресном пространстве памяти по адресу 255 (0xFF). Как и в обычном ПК, если вам нужен доступ к, например, шине PCI Express, вы тоже обращаетесь определённым адресам в пространстве памяти центрального процессора.

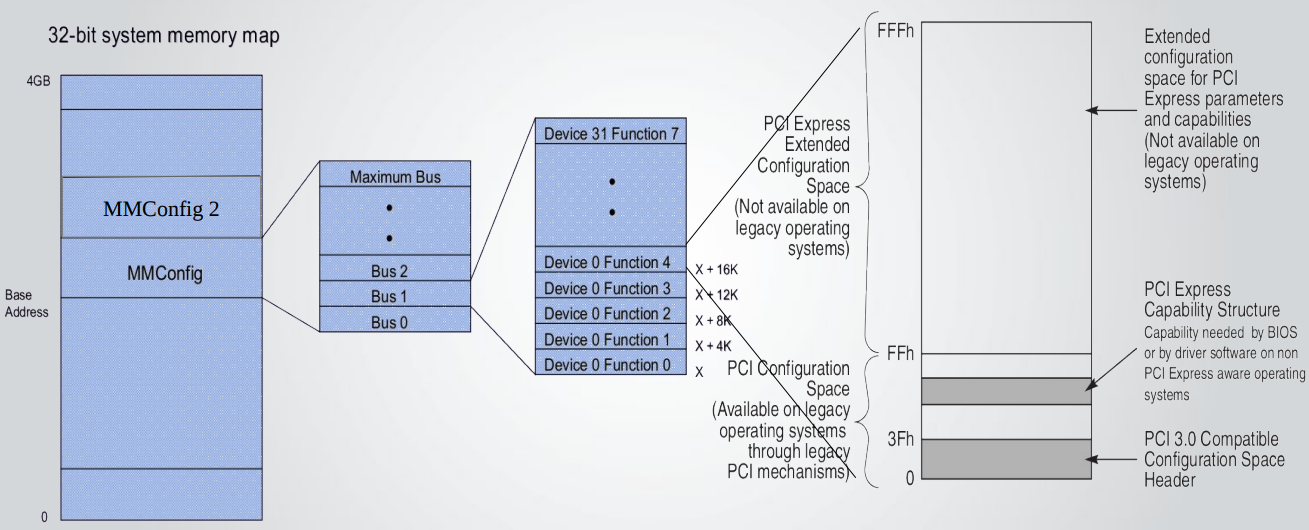
Если обратиться к этому адресу, то обращение перейдёт на порт ввода-вывода:

class Memory:
  __MEMORY_SIZE = 255
  __IO_ADDRESS = 255

  def __init__(self):
      self.image = [0 for i in range(self.__MEMORY_SIZE)]

  def read(self, addr):
      if 0 <= addr < self.__MEMORY_SIZE:
          return self.image[addr]
      elif addr == self.__IO_ADDRESS:
          return int(input("Enter a value > "))
  
  def write(self, addr, w_data):
      if 0 <= addr < self.__MEMORY_SIZE:
          self.image[addr] = w_data
      elif addr == self.__IO_ADDRESS:
          print("Output > ", w_data)

Но не всё так просто. Здесь 16-битная память, и если вводить или выводить через консоль отрицательные числа, то всё пойдёт крахом.

Python не лучший выбор, когда нужно работать с данными определённого типа и размера. Поэтому будем обрезать байты вспоминая дополнительный код:

def read(self, addr):
    if 0 <= addr < self.__MEMORY_SIZE:
        return self.image[addr]
    elif addr == self.__IO_ADDRESS:
        r_data = int(input("Enter a value > "))
        if r_data < 0:
            r_data = 0x10000 + r_data	# two's-complement
        return r_data

def write(self, addr, w_data):
    if 0 <= addr < self.__MEMORY_SIZE:
        self.image[addr] = w_data
    elif addr == self.__IO_ADDRESS:
        if w_data > 0x7FFF:
            w_data =  w_data - 0x10000	# two's-complement
        print("Output > ", w_data)

Теперь изменим существующую программу суммирования, чтобы значения слагаемых извлекались из устройства ввода-вывода:

computer.memory.write(0x10, 0x83FF) # загружаем значение из консоли в R[3]
computer.memory.write(0x11, 0x84FF) # загружаем значение из консоли в R[4]
computer.memory.write(0x12, 0x1234) # суммируем R[3] и R[4] и помещаем в R[2]
computer.memory.write(0x13, 0x92FF) # выводим в консоль значение R[2]

Запускаем:

# python toy.py
Enter a value > 123
Enter a value > -456
Output > -333
HALT

Огонь! Добавим загрузку внешнего файла и напишем что-нибудь посложнее.

Умножение трёх чисел в TOY

Добавим загрузку внешнего файла в TOY. Вообще порядок байт в TOY это little-endian (LE), и соответственно загружаемый файл тоже должен быть типа LE. Но предлагаю сделать файл в формате BE для большей читаемости, а при его загрузке в память TOY будем просто менять старшие и младшие байты местами:

def load_app(self, filename):
    with open(filename, 'rb') as file:
        file_contents = file.read()
        file_length = len(file_contents) // 2
        for addr in range(file_length):
            self.memory.write(self.SOFT_START_ADDRESS + addr, 
                  # change BE to LE
                  (int(file_contents[addr * 2]) << 8) | 
                  int(file_contents[(addr * 2) + 1]))

...

for a in sys.argv[1:]:
	self.load_app(a)

Напишем вычисление x * y * z. Чтобы не повторять два раза код умножения будем выполнять умножение в отдельной функции умножения. Итак, для начала напишем в псевдокоде:

R[A] = input() # сохраняем первое число из консоли в R[A]
R[B] = input() # а второе число в R[B]
R[F] = PC; goto multiple # умножаем R[A] на R[B] и сохраняем в R[C] в функции multiple
R[A] = R[C] # перемещаем результат умножения в R[A]
R[B] = input() # снова сохраняем число из консоли в R[B]
R[F] = PC; goto multiple # опять умножаем
print(R[C]) # печатаем
halt # завершаем работу

Сама функция умножения:

multiple: R[C] = 0 # в R[C] хранится результат умножения, сбрасываем его
R[1] = 1 # нам понадобится декрементить на 1, будем использовать для этого R[1] 
check: if (R[A] == 0) goto end # или while (R[A] != 0)
R[C] += R[B] # добавляем значение к результату
R[A]-- # декрементим
goto check # проверяем нужно ли продолжать умножать
end: PC = R[F] # выходим из функции на уровень выше

Теперь перенесём всё на машинный код TOY:

10: 8aff # R[A] = input()
11: 8bff # R[B] = input()
12: ff18 # R[F] = PC; goto multiple
13: 1ac0 # R[A] = R[C]
14: 8bff # R[B] = input()
15: ff18 # R[F] = PC; goto multiple
16: 9cff # print(R[C])
17: 0000 # halt
18: 7c00 # multiple: R[C] = 0
19: 7101 # R[1] = 1
1A: ca1e # check: if (R[A] == 0) goto end
1B: 1ccb # R[C] += R[B]
1C: 2aa1 # R[A]--
1D: c01a # goto check
1E: ef00 # end: PC = R[F]

Остаётся создать пустой файл mult.bin, открыть его в каком-нибудь hex-редакторе и записать по байтам:

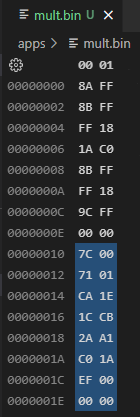
Для проверки умножим 12 на -34 на 56:

# python
>>> 12 * (-34) * 56
-22848

Пора жать кнопку "Пуск". Запускаем TOY:

# python toy.py mult.bin
Enter a value > 12
Enter a value > -34
Enter a value > 56
Output > -22848
HALT

P.S. Как видите, всё гениально и просто. Современные компьютеры - это самые сложные изобретения цивилизации, но и они состоят из простейших элементов управляемых простейшими командами. Кому понравилась эта тема, можете копнуть дальше и найти в сети исходники эмуляторов на Python, например, Intel 4004 или Z80. Теперь разобраться будет легко.

Исходники

Фото на обложке:
The women who changed the history of computing