
Когда я разбирался с программируемыми калькуляторами, то думал, как бы элегантнее протестировать функциональность устройства. Один из известных способов проверки – это реализация какой-либо игры.
Игр для калькуляторов, как на просторах бывшего СССР, так и за рубежом громадное количество, остаётся только выбрать. Наиболее популярная — это «Посадка на Луну». Однако, для меня она показалась скучной и неинтересной, а сам код сложным и запутанным. Поэтому мой выбор пал на крестики-нолики, так как все мы играли в них в школе, и мне стало интересно сыграть в неё с калькулятором.
Реализовать игру решил на модели HP-32S, поскольку он мне очень полюбился за красоту архитектурной реализации и удобство программирования.
❯ Основа программы
В предыдущей своей статье "Калькуляторы с обратной польской нотацией" я делал обзор литературы для программируемых калькуляторов. Среди которой была замечательная книга А.Г. Гайшут "Калькулятор твой помощник и соперник в играх".
В этой книге приводится огромное количество примеров игр на калькуляторе и, в частности, пример игры в крестики-нолики:

Мне не удалось найти описания логики работы этих игр, а автор книги, к сожалению, умер в 2015 году. Попытка искать ответ в публикациях автора, любезно предоставленных на его личном сайте, не увенчалась успехом.
Поэтому придётся разбираться с этой программой самостоятельно. Приведу текст и описание программы из книги под спойлером:
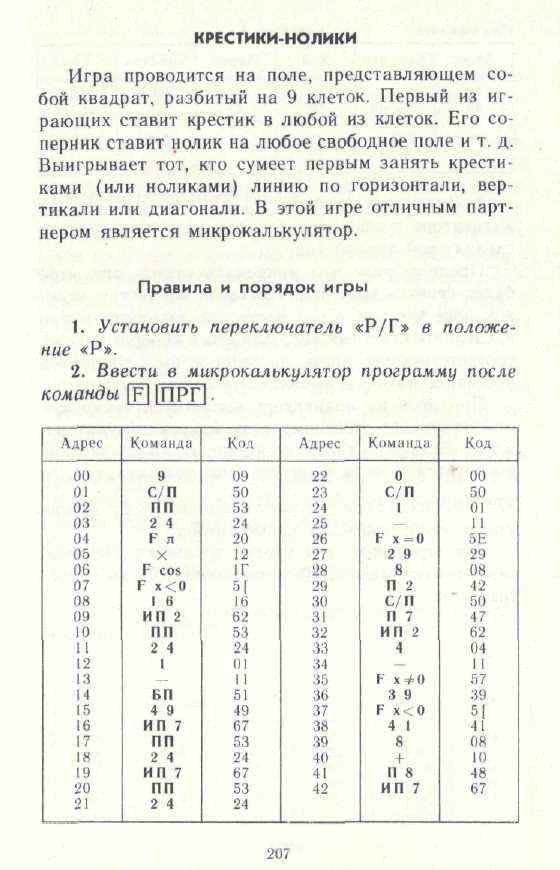

Главная задача – это перенос этого кода с МК-61 на калькулятор HP-32S. Для начала, разберёмся как эта программа работает.
❯ Проверка программы на МК-61
Первое, что я сделал – это перенабрал код из книги в формате, который понимает онлайн-эмулятор МК-61.
00.9 01.С/П 02.ПП 03.24 04.Fпи 05.x 06.Fcos 07.Fx<0 08.16 09.ИП2
10.ПП 11.24 12.1 13.- 14.БП 15.49 16.ИП7 17.ПП 18.24 19.ИП7
20.ПП 21.24 22.0 23.С/П 24.1 25.- 26.Fx=0 27.29 28.8 29.П2
30.С/П 31.П7 32.ИП2 33.4 34.- 35.Fx#0 36.39 37.Fx<0 38.41 39.8
40.+ 41.П8 42.ИП7 43.- 44.Fx=0 45.48 46.ИП2 47.В/О 48.ИП8 49.7
50.7 51.С/П 52.0 53.0 54.0 55.0 56.0 57.0 58.0 59.0
60.0 61.0 62.0 63.0 64.0 65.0 66.0 67.0 68.0 69.0
70.0 71.0 72.0 73.0 74.0 75.0 76.0 77.0 78.0 79.0
80.0 81.0 82.0 83.0 84.0 85.0 86.0 87.0 88.0 89.0
90.0 91.0 92.0 93.0 94.0 95.0 96.0 97.0 98.0 99.0
A0.0 A1.0 A2.0 A3.0 A4.0 Кстати, если интересно, то можно попробовать поиграть в эмуляторе, чтобы понять принцип работы. Для этого копируем код, вставляем в область «Код программы:» и нажимаем кнопку «Ввести в память». Картинка из книжки выше подсказывает нам, что калькулятор даёт координаты, куда ставить "X", а мы ему в ответ передаём координаты, куда ставить "O".
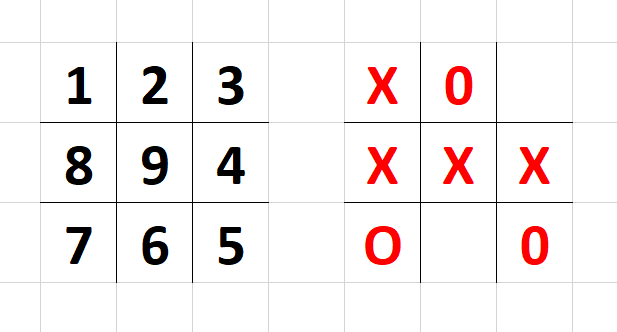
Координаты для игры
Чтобы начать играть на клавиатуре калькулятора, нужно нажать кнопку [С/П]. В ответ будет выведено число, первое число всегда «9» (центр поля). В ответ необходимо ввести свою координату, например, «2» и нажать [С/П]. И так далее, пока вы не проиграете (калькулятор выведет «77», либо будет ничья (калькулятор выведет «0»).
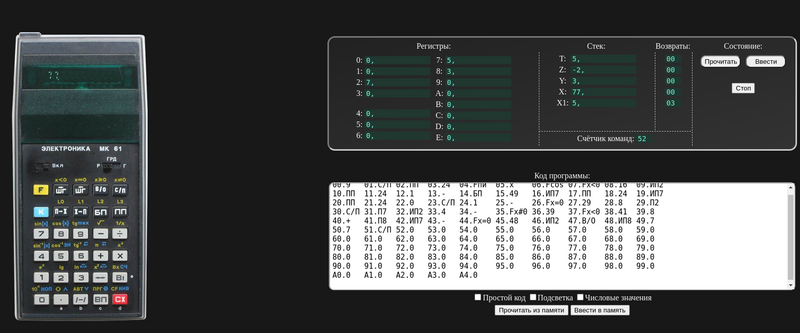
Калькулятор победил
Чтобы посмотреть последний ход калькулятора, надо обменять регистры X и Y местами, для этого нужно нажать на клавишу [⟷].
Проверка показала, что всё прекрасно работает как в эмуляторе, так и на живом калькуляторе, и ошибок в программе нет.
❯ Анализ кода программы для калькулятора МК-61
Для понимания работы программы, я переписал её на python. Конечно, даже при переносе на привычный язык программирования, код будет выглядеть немного диковато, поскольку реализовывался на совершенно иных принципах, но он хотя бы будет читаемым для остальных пользователей.
Особенность программирования МК-61 в том, что он пропускает команду перехода, если условие истинно, и исполняет — если ложно! Поэтому все условия для python пришлось инвертировать. Плюс, я для удобства ввёл дополнительные функции, которые также перенёс впоследствии в HP-32S: функция вывода координат крестиков и ввода ноликов, функция ничья и победа калькулятора:
def calc_win():
global x
print(f"Calc winer! x={x}")
exit()
def draw_win():
print(f"Draf... x={x}")
exit()
def input_x():
global x
global y
y = x
print(x)
x = int(input())
Первое – инициализирую регистры калькулятора:
x = 0
y = 0
p2 = 0
p7 = 0
p8 = 0После всех подпрограмм идёт головная программа:
x = 9 #00.9
input_x() #01.С/П
subprog() #02.ПП #03.24
x = x * math.pi #04.Fпи #05.x
x = math.cos(x) #06.Fcos
if x < 0: #07.Fx<0
x = p2 #09.ИП2
subprog() #10.ПП #11.24
x = x - 1 #12.1 #13.-
calc_win() #14.БП #15.49
x = p7 #16.ИП7
subprog() #17.ПП #18.24
x = p7 #19.ИП7
subprog() #20.ПП #21.24
#x = 0 #22.0
draw_win() #23.С/П Можно увидеть, что в любом случае в самом начале крестик будет стоять на координате 9. Вся основная логика сокрыта в подпрограмме.
def subprog():
global x
global y
global p2 #A
global p7 #B
global p8 #C
x = x - 1 #24.1 #25.- #27.29
if x == 0: #26.Fx=0
x = 8 #28.8
p2 = x #29.П2
input_x() #30.С/П
p7 = x #31.П7
x = p2 #32.ИП2
x = x - 4 #33.4 #34.-
if (x <= 0): #35.Fx#0 #36.39 #37.Fx<0 #38.41
x = x + 8 #39.8 #40.+
p8 = x #41.П8
x = x - p7 #42.ИП7 #43.-
if (x == 0):#44.Fx=0
x = p2
else:
x = p8
calc_win()Из всего кода я понял, что второй ход калькулятора будет на единицу меньше оппонента, а если ход был в координату «1», то равен восьми. Но вот что делает остальная логика программы, особенно зачем там тригонометрическая функция, для меня осталось загадкой. Буду рад читателям, если кто-то сможет прояснить, как же работает эта программа.
Исходный код доступен в репозитории проекта.
И, да, код вполне себе работоспособен, в чём несложно убедиться:
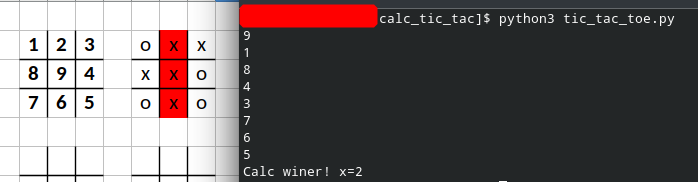
❯ Перенос кода на HP-32S
Напомню, что калькулятор HP-32S, который есть у меня, принадлежит семейству калькуляторов HP10B/14B/17B/17BII/19BII/20S/21S/22S/27S/28S/32S/32SII/42S, таким образом, всё, что приводится ниже, с небольшими адаптациями можно будет перенести и на другие модели этой серии.Трудозатраты в предыдущей главе, по переносу кода на python, были проделаны с двумя целями:
- Понять, как же работает этот код (увы, не выполнено).
- Более удобно переносить на другую модель калькулятора.
Вооружившись документацией на калькулятор HP-32S, я переписал программу крестиков-ноликов с питона для него. Для удобства я делал это в таблицах Exel. Как я уже говорил, особенность калькулятора в том, что он маркирует каждую строку буквой и цифрой, а любая метка – это смена буквы. Таблицы идеально подходят для этого.
Ниже под спойлером, приведён код программы. Если вы хоть немного знаете ассемблер и какой-то другой язык программирования, хоть тот же BASIC, то без труда сможете понять, что же там происходит.
| Addr | CMD | Comment |
|---|---|---|
| 001 | 9 | |
| 002 | XEQ I | Call input |
| 003 | XEQ S | Call subrog |
| 004 | π | |
| 005 | * | |
| 006 | COS | |
| 007 | x > 0 | |
| 008 | GTO A | |
| 009 | RCL A | |
| 010 | XEQ S | Call subrog |
| 011 | 1 | |
| 012 | - | |
| 013 | GTO E | End |
| A01 | LBL A | |
| A02 | RCL B | |
| A03 | XEQ S | Call subrog |
| A04 | RCL B | |
| A05 | XEQ S | Call subrog |
| A06 | STO X | |
| A07 | VIEW X | |
| A08 | 0 | Draw |
| A09 | STO E | |
| A10 | VIEW E | SHOW |
| A11 | STOP | End |
| S01 | LBL S | |
| S02 | 1 | |
| S03 | - | |
| S04 | x <> 0 | |
| S05 | GTO T | |
| S06 | 8 | |
| T01 | LBL T | |
| T02 | STO A | |
| T03 | XEQ I | Call input |
| T04 | STO B | |
| T05 | RCL A | |
| T06 | 4 | |
| T07 | - | |
| T08 | x = 0 | |
| T09 | GTO U | |
| T10 | x > 0 | |
| T11 | GTO V | |
| U01 | LBL U | |
| U02 | 8 | |
| U03 | + | |
| V01 | LBL V | |
| V02 | STO C | |
| V03 | RCL B | |
| V04 | - | |
| V05 | x <> 0 | |
| V06 | GTO C | |
| V07 | RCL A | |
| V08 | RTN | |
| C01 | LBL C | |
| C02 | RCL C | |
| E01 | LBL E | End of program Calc win |
| E02 | STO X | |
| E03 | VIEW X | |
| E04 | 77 | |
| E05 | STO E | |
| E06 | VIEW E | |
| E07 | STOP | |
| I01 | LBL I | |
| I02 | STO X | Input Subroutines |
| I03 | VIEW X | |
| I04 | INPUT O | |
| I05 | RTN |
В силу того, что на калькуляторе HP-32S можно сделать вывод на экран конкретного регистра (с указанием имени регистра), а также запрос ввода другого конкретного регистра, то ввод-вывод становится чуть более интерактивным и интересным.
Лучше один раз увидеть, чем тысячу раз прочитать.
❯ Выводы
Изначально задача казалась мне такой простой, но заняла у меня достаточно приличное время. Её ценность состояла в том, что мне удалось разобраться — как же программировать для калькулятора HP-32S. В результате оказалось, что из модельного ряда калькуляторов, с которыми я занимался — эта версия оказалась самая дружелюбная и удобная.
Другой задачей, которую я хотел решить — это разобраться, каким образом изобретались подобные программы для микрокалькуляторов. Из-за того, что у калькулятора ограничена память программ, производилась какая-то дичайшая оптимизация, поэтому она выглядит так запутанно. Но, к моему сожалению, ни толковой литературы, ни описания, как это делалось, мне не удалось найти.
Поэтому, если у вас, уважаемые читатели, есть идеи о том, как же работает программа крестики-нолики (можно анализировать код python), то я с удовольствием их выслушаю.
❯ Полезные ссылки:
- Гитхаб этого проекта
- Первая часть «Калькуляторы с обратной польской нотацией»
- Сайта автора «Гайштут и его друзья»
- Онлайн-эмулятор МК-61
- Документация на калькулятор HP-32S
Если вам интересна металлообработка, старое железо, всякие DIY штуки, погроммирование и linux, то вы можете следить за мной ещё в телеграмме.
Возможно, захочется почитать и это:
- ➤ Shadow Empire. Пошаговый гибрид 4Х стратегии и варгейма
- ➤ DMX голова: трепанация черепа и замена мозга (превращение в 3D платформу)
- ➤ Полигон для творчества за 1500 р. Экран, Малина, OpenOCD и бусики
- ➤ Применение чистой архитектуры в Go
- ➤ Карманный компьютер из 1985 года: программируемый калькулятор «Электроника МК-54»
Новости, обзоры продуктов и конкурсы от команды Timeweb.Cloud — в нашем Telegram-канале ↩

Комментарии (18)

udik_chudik
29.04.2024 08:31+3Круто! Все мое детство прошло за написанием програм для МК-52 пока не собрал Специалиста))
А "посадка на Луну" кстати была в 2х вариантах: в упрощенном чисто вертикальном режиме, и в режиме с заданным местом посадки! Но как по мне интереснее было авторалли и морской бой, хотя он был и не очень

BorysL
29.04.2024 08:31+3Как я понял, функция cos в программе используется в качестве нахождения остатка от деления по модулю 2 (сишное выражение %). То есть cos(1*pi), cos(3*pi), cos(5*pi) == -1,
а cos(2*pi), cos(4*pi), cos(6*pi) == +1.

RumataEstora
29.04.2024 08:31Из-за того, что у калькулятора ограничена память программ, производилась какая-то дичайшая оптимизация, поэтому она выглядит так запутанно. Но, к моему сожалению, ни толковой литературы, ни описания, как это делалось, мне не удалось найти.
Ребятишки узнали про аппаратные ограничения и возможности/способы эти ограничения обойти.

dlinyj Автор
29.04.2024 08:31+3Что-то не встречал молодежи, которые занимаются калькуляторами. Моим детям эта древность уж точно не интересна. Хотя тоже программисты.
Или вы кого-то другого имели в виду?

MaFrance351
29.04.2024 08:31+1Уверен, речь про молодёжь вашего времени. Когда эти калькуляторы были актуальны.

dlinyj Автор
29.04.2024 08:31Ну даже в те годы у меня не было такого калькулятора и тогда я не занимался средствами оптимизации кода на калькуляторах.
Так что я не понимаю этот неконструктивный высокомерный выпад.

Wesha
29.04.2024 08:31+6в те годы у меня не было такого калькулятора
И... что? Кого это останавливало (ну, кроме самых снежинок, хотя это слово изобретут лет на 40 позже)? У меня в те годы тоже не было такого калькулятора. Программы записывались в тетрадочку; программы, которые писал сам, отлаживались "в уме". До сих пор помню, как долго бился над программой, которая всё время получалась в 107 шагов, а памяти в МК-61 — 105. Однако после месяца измывательств таки утоптал.

MaFrance351
29.04.2024 08:31+1А что за программа была, интересно?

Wesha
29.04.2024 08:31+1Не могу вспомнить, что за программа была, но припомнил некоторые детали. Программа была из журнала, написана для МК-61 и имела 100 шагов (на Б3-34 объём памяти — 98 шагов), а у нас в кружке были только они. Очень хотелось запустить её в кружке, но из-за этого не получалось, поэтому месяц сидел и крутил так и сяк, пытаясь "умять" те самые два лишних шага. В конце концов получилось, соптимизировал. Более подробно теперь не вспомню — всё-таки 30 лет прошло.

da-nie
29.04.2024 08:31+2Возможно, понять как это работает поможет программа из вот этой книги.
Она для всеми любимого К580ВМ80А (ну и для Z80 должна подойти). Если её дизассемблировать (я бы просто в эмулятор спектрума загрузил бы Mons-4 и прошёлся бы по этой программе), то можно понять логику. Тригонометрии в ней вроде как не должно быть. Я, правда, эту программу не запускал никогда, так что не знаю, есть в ней ошибки или нет.


dlinyj Автор
29.04.2024 08:31+1Спасибо, это очень годно. Со Спектрум так просто не выйдет, надо смотреть реализацию ввода-вывода. Но логика интересна, да.

da-nie
29.04.2024 08:31+1Полагаю, ввод-вывод там простейший и виден будет сразу.
Вот набранная программа:
c000: 3e 09 32 00 90 d7 cd 1a c0 c3 47 c0 00 00 00 00
c010: 7a cd 1a c0 7a cd 1a c0 c7 00 06 01 90 c2 22 c0
c020: 3e 08 4f 32 00 90 d7 57 1e 04 d9 93 ca 32 c0 f2
c030: 35 c0 2e 08 65 6f 7a 95 ca 45 c0 00 00 26 73 7c
c040: 32 00 90 ef 76 79 c9 fe 01 ca 5e c0 fe 03 ca 5e
c050: c0 fe 05 ca 5e c0 fe 07 ca 5e c0 c3 10 c0 79 cd
c060: 1a c0 90 c3 3d c0 00 00 00 00 00 00 00 00 00 00Вот только online-дизассемблер Z80 нифига не хочет это загружать. А помещать это внутрь эмулятора спектрума и вспоминать команды Mons-4 так лень... Может, потом гляну.

edtech
29.04.2024 08:31+4Идея алгоритма более-менее понятна, попытаюсь объяснить )
Программа начинает с хода на позицию 9, после чего ожидает вашего хода. Следующий ход программы будет ваш ход минус 1 (команды 24-25), при необходимости делая переход через начало. Например, если вы походите в позицию 1, программа ответит ходом на 8, т.е. переместится в соседнюю клетку против часовой стрелки. Затем приходит ваш черед ходить, и программа рассчитывает, что потенциально выигрышный ход для неё – это её предыдущий ход минус 4. В результате происходит сравнение вашего следующего хода с этим выигрышным ходом (шаги 42-44). Если ваш ход не совпадает с выигрышным, программа переходит к шагу 48 и завершает работу, заявляя о своей победе. Однако, если вы займете рассчитанную выигрышную позицию, то программа возвращается к команде 4, где происходит проверка четности последнего хода программы. Если этот ход нечетный, то по командам 9 и последующим переходом на 24 программа делает ход на одну позицию назад от своего последнего хода, создавая таким образом "вилку" (затем пользователь должен ходить на +4, и программа выигрывает, поставив свой крестик на позицию минус 1 от своего последнего хода). Если же последний ход программы был четным, то по команде 16 и последующему переходу на 24 программа ходит на одну позицию назад от последнего хода пользователя. Та же подпрограмма (команда 24) проверяет, закрыл ли пользователь клетку "программа + 4". Если после двух таких итераций пользователь закрывает эту клетку, программа завершает игру ничьей.



MaFrance351
Очень круто! Даже захотел попробовать достать МК-61 и запустить. У меня есть такой аппарат, я запускал на нём разные программы, но сопоставимого по уровню написать особо не довелось.
Тоже было интересно. Азы программирования под этот аппарат есть в инструкции, но в наши времена реально впечатляет, как в 105 шагов смогли упихать не просто расчётные программы, а даже целые игры с сюжетом. Оптимизация тут очень на уровне.