Параметрическая идентификация линейной динамической системы / forpes.ru

Главная
Параметрическая идентификация линейной динамической системы

Параметрическая идентификация линейной динамической системы +11

11.03.2016 07:20

kostik_rusakov 13 4500 Источник

Введение

Уважаемые читатели. В настоящее время процессам идентификации динамических систем уделяется много внимания. На эту тему написано много диссертаций, дипломов и научных публикаций. В различной литературе написано много чего про идентификацию, приведены различные модели и методы. Но всё это для обывателя становится ясным не сразу. Я попытаюсь в этой статье объяснить как решать задачу параметрической идентификации, когда техническая система (объект) описывается системой дифференциальных уравнений, с помощью метода МНК.

Немного из теории

Для начала нужно понять, что такое динамическая система. Если говорить как можно проще, то это система, параметры которой изменяются во времени. Подробнее здесь. Практически любую динамическую систему можно описать дифференциальным уравнением какого-либо порядка, например:

${{dx_1\over dt}=ax_1+bx_2} \\ {dx_2\over dt}=cx_1+dx_2} .$

Данная система дифференциальных уравнений характеризуется своими параметрами. В нашем случае это a, b, c и d. Они могут быть как статическими так и динамическими.

Что означают эти коэффициенты?

Применительно к реальным физическим динамическим системам эти коэффициенты дифференциального уравнения имеют конкретную физическую привязку. Например в системе ориентации и стабилизации космического аппарата данные коэффициенты могут играть различную роль: коэффициент статической устойчивости КА, коэффициент эффективности бортового управления, коэффициент способности изменять траекторию и т.п. Подробнее здесь.

Так вот задача параметрической идентификации это определение этих самых ~~коэффициентов~~ параметров a, b, c и d.

Задача наблюдения и измерения

Стоит отметить, что для решения задачи параметрической идентификации необходимо получить «измерения» одной (или всех) фазовой координаты (в нашем случае это x₁ и (или) x₂).

Для того чтобы система была идентифицируема, она должна быть наблюдаема. То есть ранг матрицы наблюдаемости должен быть равен порядку системы. Подробнее про наблюдаемость здесь.

Наблюдение процессов, происходящих в объекте, происходит следующим образом:

$y=Hx+\xi(t).$

где:

у — вектор наблюдаемых параметров;
H — матрица связи параметров состояния и наблюдаемых параметров;

$\xi(t)$ — помеховая составляющая (в ней спрятаны все погрешности наблюдения);

Подробнее про вектора и матрицы

Динамическую систему которую мы описывали выше, можно представить в векторно-матричной форме:

${dx\over dt}=Ax+Bu+\varepsilon(t)$

где:

x — вектор состояния динамической системы. В общем случае он имеет бесконечную размерность. Но когда мы имеем дело с конкретной моделью, то уже говорим не о «векторе состояния» а о «векторе фазовых координат». В нашем примере он имеет две составляющие
$x=\begin{pmatrix}x_1\\x_2\end{pmatrix}$
A — переходная матрица. Содержит те самые коэффициенты которые нам хотелось бы найти.

$A=\begin{pmatrix}a &b\\c&d\end{pmatrix}$
u — управляющее воздействие. В нашем примере оно равно 0. То есть наш объект не управляем. Прошу обратить внимания что это просто пример, не имеющий ничего общего с какой-то реально существующей системой.
B — матрица управления.

$\varepsilon(t)$ — помеховая составляющая.

Измерение процессов, происходящих в объекте, описывается следующим образом:

${{z}=y+n(t)} \\ {z}=n_1(t)y+n_2(t)} .$

Как мы видим погрешность измерения может быть как аддитивной (в первом случае), так и мультипликативной(во втором)

Задача идентификации

Рассмотрим решение задачи параметрической идентификации в случае когда не известен один коэффициент. Перейдем к конкретному примеру. Пусть дана следующая система:

${{dx_1\over dt}=ax_1+x_2} \\ {dx_2\over dt}=0.0225x_1-0.3x_2} \\ {x_1(0)=20 \ x_2(0)=20}$

Видно, что параметры равны b = 1, c = 0.0225 и d = -0.3. Параметр a нам неизвестен. Попробуем дать его оценку с помощью метода наименьших квадратов.

Задача состоит в следующем: по имеющимся выборочным данным наблюдений за выходным сигналами с интервалом дискретизации ?t требуется оценить значения параметра, обеспечивающего минимум величины функционала невязки между модельными и фактическими данными.

$J=(y-y_m)^T(y-y_m)=e^Te=\sum\limits_{j=1}^{N}e_j^2\longrightarrow\min$

где $e_j=y_i-y_m_i$ — невязка, определённая как разность между выходом исследуемого объекта и реакцией, вычисленной по математической модели объекта.

Невязка складывается из неточностей структуры модели, погрешностей измерений и неучтённых взаимодействий среды и объекта. Однако, независимо от природы возникающих ошибок, метод наименьших квадратов минимизирует сумму квадратичной невязки для дискретных значений. В принципе, МНК не требует никакой априорной информации о помехе. Но для того, чтобы полученные оценки обладали желательными свойствами, будем предполагать, что помеха является случайным процессом типа белого шума.

Оценка $a^*$ по методу наименьших квадратов, минимизирующая критерий J, находится из условия существования минимума функционала:

$J=\min\limits_{a} J=J |_{a=a^*}$

Важным свойством оценок по МНК является существование только одного локального минимума, совпадающего с глобальным. Поэтому оценка $a^*$ является единственной. Ее значение определяется из условия экстремума функционала J:

${{\partial J\over \partial a}|_{a=a^*}=2(y-y_m)(y-y_m)^{\prime} =0$

То есть необходимо от функционала $J=(y-y_m)^2$ взять производную по a и приравнять ее к нулю.

Обращаю внимание, что $y$ — это «измеренные» значения фазовых координат $x_1$ и (или) $x_2$ , а $y_m$ — это фазовые координаты $x_1$ и (или) $x_2$ вычисленные по математической модели объекта. Но ведь в модели объекта, представленной в виде системы дифференциальных уравнений, $x_1$ и $x_2$ не выражены в явном виде. Для того, чтобы избавиться от этого ~~безумия~~ необходимо решить данную систему дифференциальных уравнений с заданными начальными условиями.

Решать можно как «вручную», так и используя какое-либо программное обеспечение. Ниже будет показано решение в MatLab. В итоге должна получится система алгебраических уравнений для каждого момента времени $t_i$ :

$Sa_i^*=y_i$

Затем подставляя вместо $y$ значения «измеренных» фазовых координат, находим оценку параметра $a_i^*$ для каждого момента времени $t_i$ .

Где взять эти «измеренные» значения фазовых координат?

Вообще эти значения берутся из эксперимента. Но так как мы никакой эксперимент не проводили, то возьмем эти значения из численного решения нашей системы дифференциальных уравнений методом Рунге-Кутта 4-5 порядка. Выберем параметр $a=-0,7$

Решение найдем встроенными функциями пакета MatLab. Подробнее здесь. Решение данным методом показано ниже.

код MatLab

function F=diffurafun(t,x)
F=[-0.7*x(1)+x(2);0.0225*x(1)-0.3*x(2)];
end
%===============================================================%
% формирование вектора начальных условий
X0=[20;20];
% формирование интервала интегрирования
interval=[0 50];
% обращение к функции оde 45
[T,X]=ode45(@diffurafun,interval,X0);
% вывод графика решения
figure; plot (T,X(:,1),'r-',T,X(:,2),'b--'); % вывод графика
legend ('Параметр х1',' Параметр х2');
grid on;

График

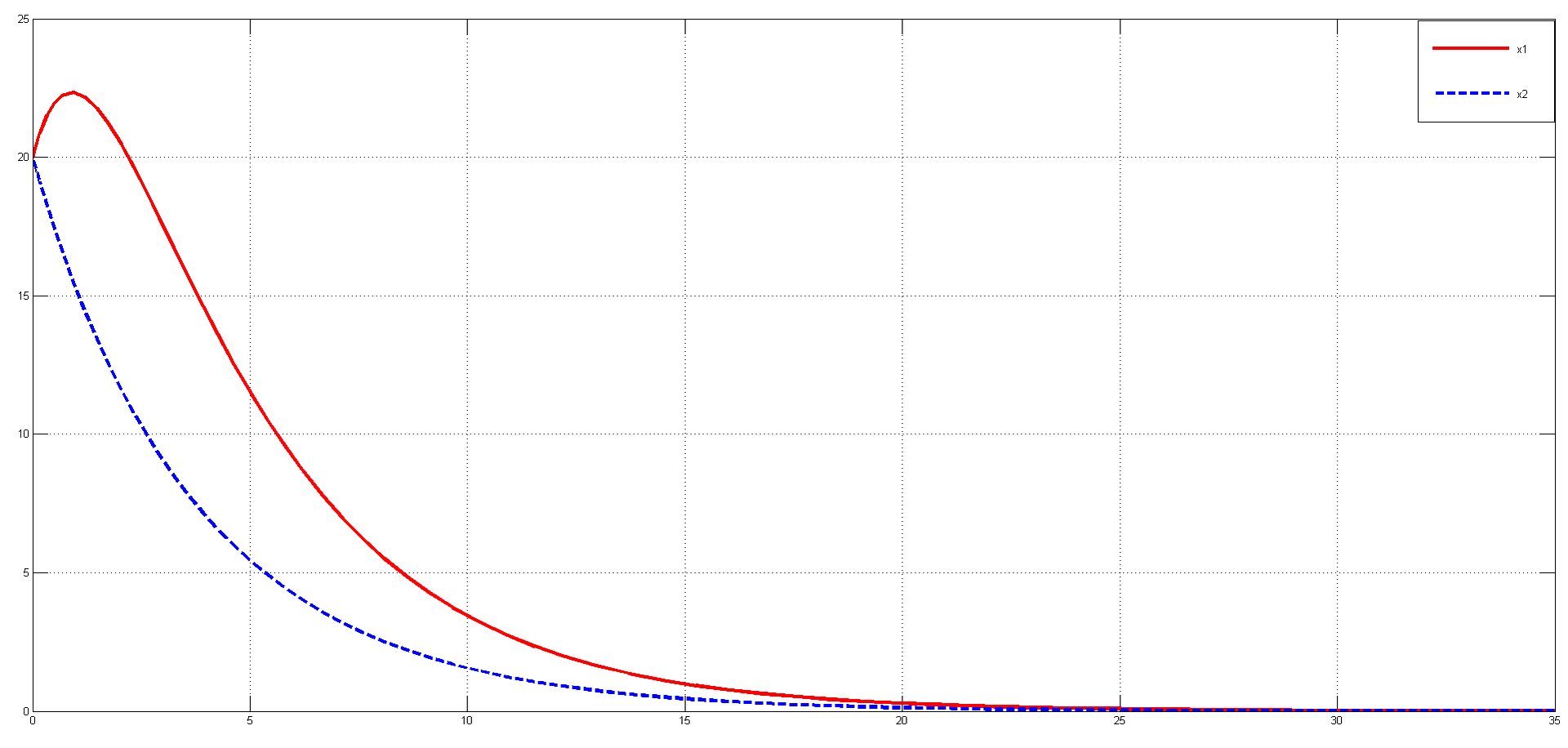
На данном графике красной сплошной линией обозначена фазовая координата $x_1$ , а синей пунктирной линией обозначена фазовая координата $x_2$

Ниже показан код на MatLab и график.

Код MatLab

% dx/dt = A*x — линейная динамическая система без управления и помех
% для начала нам необходимо решить аналитически данную СДУ
% обозначим тип переменных
syms x(t) y(t) a
% решим систему при заданных начальных условиях
S = dsolve(diff(x) == a*x + 1*y,'x(0)=20', diff(y) == 0.0225*x — 0.3*y,'y(0)=20');
% выберем решение первой фазовой координаты, так как именно в его уравнении
% содержится искомый параметр а
x(t) = S.x;
% найдем частную производную первого уравнения по параметру а (в
% соответствии с методом МНК)
f=diff(x(t),'a');
% теперь немного упростим получившееся выражение
S1=simplify(f);
% зададим переменной t массив значений T
t=T;
% найдем выражения, содержашие параметр а для каждого момента времени
SS=eval(S1);
% теперь в цикле, подставляя в каждое выражение значение «измеренной»
% первой фазовой координаты, определим параметр а для каждого момента
% времени T. Значения «измеренной» фазовой координаты берем из решения СДУ
% методом Рунге-Кутта 4-ого порядка
for i=2:81
SSS(i)=solve(SS(i)==X(i,1),a);
end
ist=zeros(length(T),1);
ist(1:length(T))=-0.7;
figure; plot(T,SSS,'b--',T,ist,'r-');
legend ('оценка параметра а','истинное значение');
grid on;

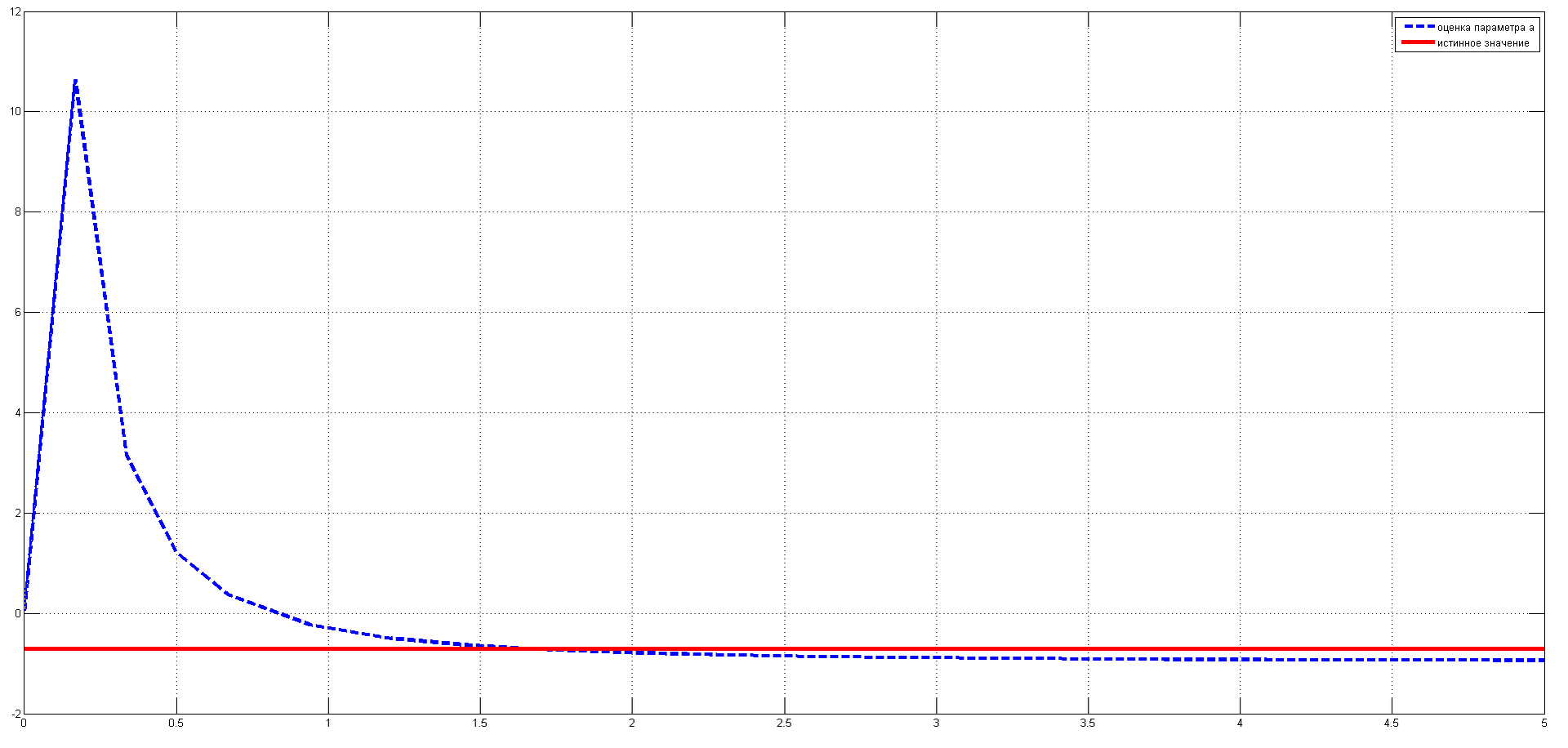
На графике синей пунктирной линией обозначена оценка параметра $a^*$ , а красной сплошной линией обозначено непосредственно «истинное» значение параметра модели $a=-0,7$ . Мы видим, что примерно на 3,5 секунде процесс стабилизируется. Небольшое расхождение оценки параметра $a^*$ и «истинного» значения вызвано ошибками при решении системы дифференциальных уравнений методом Рунге-Кутта.

Комментарии (13)

Psychopompe
11.03.2016 11:49
#8801609
Не слишком ли велика ошибка численного метода?
1. kostik_rusakov
  11.03.2016 15:02
  #8801989
  Погрешность 28 %. Да, достаточно большая. Причем там появляется систематическая погрешность. Почему именно, нужно разбираться, но мне кажется что эти ошибки возникают из-за использования встроенных алгоритмов MatLab для решения таких обратных задач. По крайней мере оценка хоть примерно сходится в направлении "истинного" значения.

Uranix
11.03.2016 12:01
#8801625
Совершенно не понимаю фразу
примерно на 3,5 секунде процесс стабилизируется
. У вас параметр a оценивается непрерывно во времени? Или когда уже известны обе траектории — модельная и фактическая? Почему такая значительная ошибка в определении а, если шума у вас нет? Самую интересную часть спрятали в код.
1. kostik_rusakov
  11.03.2016 15:06
  #8802001
  Да вы правы, некорректно написал. Параметр оценивается дискретно. И правильнее было сказать, что оценка параметра а сходится к "истинному" значению. Почему такая значительная ошибка? Уже написал выше, я думаю что это из-за использования встроенных алгоритмов для решения обратных задач. Но это мое мнение, если вы считаете по другому, напишите пожалуйста.
  1. Uranix
    11.03.2016 16:55
    #8802273
    У вас нет шума, метод Рунге-Кутты, который вы используете, дает 6-7 верных знаков при стандартных настройках. В моем понимании, оценка для а должна с самого начала совпадать с точным значением (с теми же 6-7 верными знаками). Возможно (пальцем в небо), проблема в том, что вы сравниваете численное решение с аналитическим в разных точках. Метод сравнения мне кажется очень странным, вы сравниваете два решения всего лишь в одной точке (текущей) и по этой точке оцениваете параметр. На мой взгляд, с шумом это будет работать крайне плохо. Более логично сравнивать, например, интеграл квадрата отклонения за весь промежуток времени. Хотя я бы сравнивал локальные куски решения (например, в окрестности текущего момента времени), либо вообще подставлял траекторию в диффур и искал МНК оценку для а.
    
    kostik_rusakov
    11.03.2016 18:34
    #8802443
    Точки я использую одни и те же. Эти точки "T" выходят автоматически при решении в самом начале нашей системы методом Рунге-Кутты. Потом я их же использую для параметрической идентификации.
  1. Uranix
    11.03.2016 17:08
    #8802301
    Можете объяснить, почему вы приравниваете производную от x1 по a к значению x1 из модели? У них даже размерность разная. Почему вы игнорируете вторую компоненту решения, хотя она явно фигурирует в МНК?
    
    kostik_rusakov
    11.03.2016 18:46
    #8802457
    Потому что сначала мы решаем нашу систему дифф. уравнений
    
    S = dsolve(diff(x) == ax + 1y,'x(0)=20', diff(y) == 0.0225x — 0.3y,'y(0)=20');
    
    И выбираем первую фазовую координату, потому что она содержит наш искомый параметр
    
    x(t) = S.x;
    
    Эта фазовая координата и есть $x_1$
    Затем в цикле
    
    for i=2:81
    SSS(i)=solve(SS(i)==X(i,1),a);
    end
    
    приравниваем SS (это модельные значения $x_1$ ) к X(i,1) (это измеренные значения первой фазовой координаты $x_1$ ) для того чтобы найти оценку $a^*$ в моменты времени T
    
    Игнорирую вторую фазовую координату, так как в данный момент она не нужна. И мы можем вообще изначально установить что мы её не наблюдаем.
    
    Uranix
    12.03.2016 02:25
    #8802845
    SS — это производная x по a.
    f=diff(x(t),'a'); S1=simplify(f); SS=eval(S1);

R9A_019
11.03.2016 13:57
#8801849
А что мешало, взять оптимальный фильтр Калмана-Бьюси для линейной системы, расширить пространство состояний одним уравнением вашего параметра и решить полученную систему любым методом с любой точностью? и ошибка будет стремится к нулю, для линейной системы точно. пруф — справочник по теории автоматического управления А.А. Красовского.
1. kostik_rusakov
  11.03.2016 15:12
  #8802025
  Я не стремился решить эту задачу наилучшим способом. Просто на этом примере я хотел показать решение задачи параметрической идентификации методом наименьших квадратов , когда модель задана в виде системы линейных дифференциальных уравнений. Безусловно фильтр Калмана лучше справился бы с этой задачей.

Roman_Kh
11.03.2016 21:27
#8802673
Важным свойством оценок по МНК является существование только одного локального минимума, совпадающего с глобальным.

Вообще говоря, это не верно. Минимум будет единственным только в случае выпуклости оптимизируемого функционала. А он будет выпуклым далеко не для всех распределений, поэтому априорные сведения о случайной ошибке все же не будут лишними.

Поэтому оценка a* является единственной.

При фреквентистском подходе к оцениванию, оценка по МНК для выпуклого функционала будет единственной.
Но это, вообще говоря, не единственная оценка искомого параметра a.
А если перейти на байесовы методы, то a вообще является распределением.
1. kostik_rusakov
  11.03.2016 21:47
  #8802687
  Согласен с Вами, спасибо за замечание.