Статья написана об использовании алгоритма вычисления расстояния Левенштейна для нечеткого поиска в тексте, без использования вспомогательного словаря.
Расстояние Левенштейна используется для сравнения двух слов или двух строк, чтобы определить их схожесть. Некоторое время назад передо мной встала схожая задача — в заданной строке искать вхождение слов, словосочетаний и формул, похожих на образец.
Для начала — сам алгоритм Вагнера-Фишера для вычисления расстояния Дамерау-Левенштейна. Почитать можно тут и тут.
Пример исходного кода взят из wiki.
В нем переименованы row в column, чтобы иллюстрации совпадали с кодом.
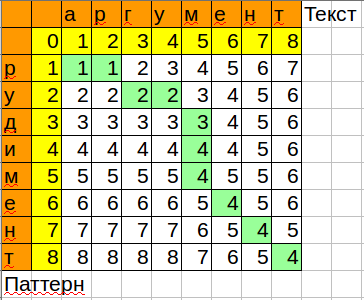
Формула для воспроизведения в calc/excel:
Обратите внимание, как алгоритм оптимизирован по памяти, хранятся только текущая и предыдущая колонка.
Задача поиска отличается от задачи сравнения тем, что нам не важно, что было до совпадения и что будет после. Потому:
— начальная цена сопоставления с текущим символом текста равна нулю, а не позиции этого символа
— результатом является не правый нижний угол таблицы, а минимальное значение в последней строке
— оптимизация, при которой может произойти замена текста и искомого шаблона (если искомый шаблон длиннее текста), здесь лишняя
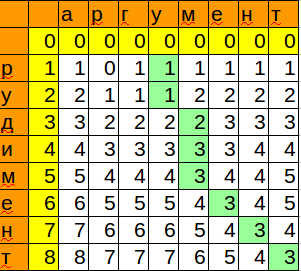
Мы запомнили позицию и минимальное значение, которое получили при сопоставлении шаблона с очередным символом. Таким образом, мы получили место, куда можно с минимальными изменениями вставить наше слово.
Последний штрих — получить всю информацию по совпадению.
P.S.: В «Тёмная комната» проще найти «Чёрная кошка», чем «Белый питбуль».
Расстояние Левенштейна используется для сравнения двух слов или двух строк, чтобы определить их схожесть. Некоторое время назад передо мной встала схожая задача — в заданной строке искать вхождение слов, словосочетаний и формул, похожих на образец.
Небольшая история, как такая мутация алгоритма вообще возникла
После ознакомления с задачей, но до начала работы над ней, я ушел в отпуск и отправился на поезде к родственникам. Дорога не близкая — 8 часов пути, интернета нет. Что у человека обычно возникает в первый день отпуска? Правильно, желание поработать. Рефлекс.
Об алгоритме Вагнера-Фишера я читал, но сохранить его куда-либо не догадался (в отпуск же собрался). И вот, под стук колес я рисую матрицы. Как уснешь, когда редакционное расстояние между словами не считается. После получения удовлетворительного результата, я записываю алгоритм на бумажку и, с чувством выполненного долга, засыпаю.
На следующий день, после сравнения записей и реального алгоритма я обнаружил в них небольшое различие, меняющее область применения задачи. Если оригинальный алгоритм подходит для сравнения двух слов и определения «сколько символов одного слова нужно удалить/добавить/заменить, чтобы получилось второе слово», то мутировавший решает другую задачу — «сколько символов первой строки нужно удалить/добавить/заменить, чтобы она целиком вошла во вторую строку». Подобных реализаций алгоритма я не встречал, если применяется где-то — пишите.
Об алгоритме Вагнера-Фишера я читал, но сохранить его куда-либо не догадался (в отпуск же собрался). И вот, под стук колес я рисую матрицы. Как уснешь, когда редакционное расстояние между словами не считается. После получения удовлетворительного результата, я записываю алгоритм на бумажку и, с чувством выполненного долга, засыпаю.
На следующий день, после сравнения записей и реального алгоритма я обнаружил в них небольшое различие, меняющее область применения задачи. Если оригинальный алгоритм подходит для сравнения двух слов и определения «сколько символов одного слова нужно удалить/добавить/заменить, чтобы получилось второе слово», то мутировавший решает другую задачу — «сколько символов первой строки нужно удалить/добавить/заменить, чтобы она целиком вошла во вторую строку». Подобных реализаций алгоритма я не встречал, если применяется где-то — пишите.
Для начала — сам алгоритм Вагнера-Фишера для вычисления расстояния Дамерау-Левенштейна. Почитать можно тут и тут.
Пример исходного кода взят из wiki.
В нем переименованы row в column, чтобы иллюстрации совпадали с кодом.
def distance(a, b):
"Calculates the Levenshtein distance between a and b."
n, m = len(a), len(b)
if n > m:
# Make sure n <= m, to use O(min(n,m)) space
a, b = b, a
n, m = m, n
current_column = range(n+1) # Keep current and previous column, not entire matrix
for i in range(1, m+1):
previous_column, current_column = current_column, [i]+[0]*n
for j in range(1,n+1):
add, delete, change = previous_column[j]+1, current_column[j-1]+1, previous_column[j-1]
if a[j-1] != b[i-1]:
change += 1
current_column[j] = min(add, delete, change)
return current_column[n]
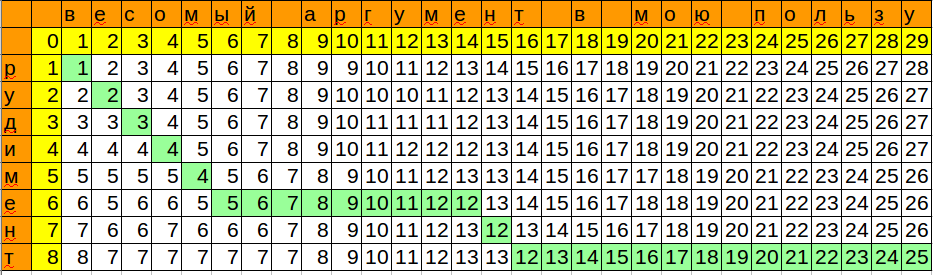
print distance(u'аргумент', u'рудимент') # 4
print distance(u'весомый аргумент в мою пользу', u'рудимент') # 25


Формула для воспроизведения в calc/excel:
=MIN(B3+1;C2+1;B2+IF($A3=C$1;0;1))
Обратите внимание, как алгоритм оптимизирован по памяти, хранятся только текущая и предыдущая колонка.
Задача поиска отличается от задачи сравнения тем, что нам не важно, что было до совпадения и что будет после. Потому:
— начальная цена сопоставления с текущим символом текста равна нулю, а не позиции этого символа
— результатом является не правый нижний угол таблицы, а минимальное значение в последней строке
— оптимизация, при которой может произойти замена текста и искомого шаблона (если искомый шаблон длиннее текста), здесь лишняя
def distance_2(text, pattern):
"Calculates the Levenshtein distance between text and pattern."
text_len, pattern_len = len(text), len(pattern)
current_column = range(pattern_len+1)
min_value = pattern_len
end_pos = 0
for i in range(1, text_len+1):
previous_column, current_column = current_column, [0]*(pattern_len+1) # !!!
for j in range(1,pattern_len+1):
add, delete, change = previous_column[j]+1, current_column[j-1]+1, previous_column[j-1]
if pattern[j-1] != text[i-1]:
change += 1
current_column[j] = min(add, delete, change)
if min_value > current_column[pattern_len]: # !!!
min_value = current_column[pattern_len]
end_pos = i
return min_value, end_pos
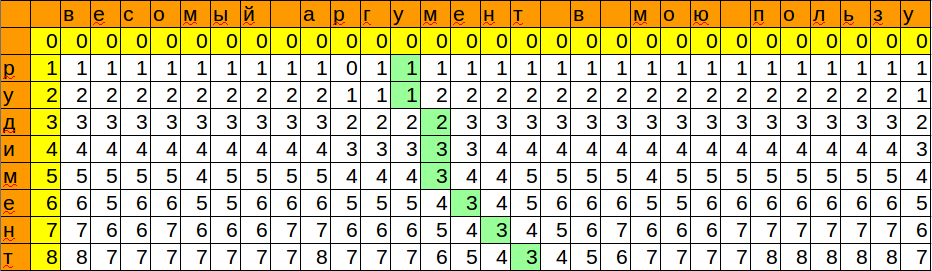
print distance_2(u'аргумент', u'рудимент') #3, 8
print distance_2(u'весомый аргумент в мою пользу', u'рудимент') #3, 16


Мы запомнили позицию и минимальное значение, которое получили при сопоставлении шаблона с очередным символом. Таким образом, мы получили место, куда можно с минимальными изменениями вставить наше слово.
Последний штрих — получить всю информацию по совпадению.
def distance_3(text, pattern):
min_value, end_pos = distance_2(text, pattern)
min_value, start_pos = distance_2(text[end_pos-1::-1], pattern[::-1])
start_pos = end_pos - start_pos
return min_value, start_pos, end_pos, text[start_pos:end_pos], pattern
print distance_3(u'аргумент', u'рудимент') # 3 3 8 умент рудимент
print distance_3(u'весомый аргумент в мою пользу', u'рудимент') # 3 11 16 умент рудимент
P.S.: В «Тёмная комната» проще найти «Чёрная кошка», чем «Белый питбуль».
print distance_3(u'Тёмная комната', u'Чёрная кошка') # 4 1 12 ёмная комна Чёрная кошка
print distance_3(u'Тёмная комната', u'Белый питбуль') # 12 6 7 Белый питбуль
Комментарии (7)

Nepherhotep
18.03.2016 14:06+1В fuzzywuzzy есть похожая функциональность — partial_ratio, которое, в отличие от ration, ищет соответствие наилучшего вхождения в строку.

kotbajan
18.03.2016 21:43Большое спасибо, действительно похожая функция. Правда немного не подходит для моей конечной цели — находить место, где встретилось похожее слово.

izvolov
18.03.2016 19:47+4Во-первых, Дамерау тут и не пахнет.
Во-вторых, алгоритм не Левенштейна, а Вагнера-Фишера. Левенштейн и Дамерау-Левенштейн — это расстояния.
Скопировать из интернета и слегка подредактировать код, толком не разобравшись в том, что он делает, и как это всё вообще называется — серьёзная тема для статьи, да.
kotbajan
18.03.2016 22:02+2Мне не нравится ваш тон, но это не отменяет того факта, что вы правы. Подредактировал статью


ServPonomarev
Прекрасно, но надо сделать следующие шаги — вычислить вероятности замены, вставки, удаления и перестановки для каждой из букв с учётом её окружения. Есть типовые опечатки (замены гласных, соседние кнопки на клавиатуре) и их шансы намного выше всех остальных возможных типов.