
Большинство трейдинговых систем создано по типу «срубить денег по-быстрому». Они обращаются к временным неэффективностям рынков, для того чтобы получить ежегодную прибыль в районе 100%. За такими системами нужен постоянный контроль. Их нужно адаптировать к условиям рынка. Но срок их жизни остается относительно небольшим. И, когда это время приходит, смерть системы сопряжена, как правило, с большими финансовыми потерями. Что если оставаться в выигрыше, но сделать работу с трейдинговой системой более комфортной и безопасной?
Предлагаем вам адаптированный перевод статьи в The Financial Hacker, в которой автор реабилитирует идею Марковица и его подход оптимизации среднего отклонения (Mean-Variance Optimization).
«Старый-добрый» подход к осуществлению инвестиций гласит: покупай активы с низкими рисками и жди. Каждый инвестиционный портфель имеет некий средний гарантированный доход и определенный уровень ценовых колебаний. Обычно мы стремимся минимизировать последний и увеличить первый показатель. Оптимальное распределение капиталов, как раз, и призвано решить эту проблему. Оно подразумевает неравноценное распределение вложенных средств по количеству N активов. Самый простой способ решить задачу увеличения средней доходности при минимизации рисков предложил 60 лет назад Гарри Марковиц. Это решение принесло ему Нобелевскую премию.
Устаревший Марковиц
К сожалению, о Марковице основательно забыли. Хотя проблема осталась: в любой трейдинговой системе приходится рассчитывать оптимальное распределение в ретроспективе. В реальном трейдинге оптимизированный таким способом портфель мистическим образом проваливается. Считается, что обычный доход на практике меньше 1/N капитальных вложений. Недавно появилась статья, автор котрой решил оспорить это утверждение. Вот, что говорится в первом параграфе этого исследования:
«Оптимизация среднего отклонения (MVO), введенная Марковицем в 1952 году, рассматривается сегодня как красивая, но бесполезная на практике теория. Ее называют нестабильной и ошибочной процедурой. Говорят, что, раз она основана на подсчете средних, волатильности и корреляциях прибыли активов, то малейшая ошибка на входе, делает применение этой оптимизации бессмысленным».
На самом деле, поставить верные данные на входе в систему – не такая уж большая проблема. Да и самих параметров расчета немного. Но почему-то такой оптимизированный портфель у критиков Марковица действительно не работает. Вероятно, они что-то делают не так. Например, используют слишком длинные периоды возврата к среднему для выборки. Или применяют алгоритм MVO неверно, смешивая короткие и длинные портфели. При корректном применении периодов моментума и исключительно длинных портфелях инвестиций, MVO выдает результат за пределами выборки намного превышающий показатель 1/N. Не верите? Смотрите пример тестирования данного алгоритма на R в блоге Ильи Киприса.
Реализация на R – редкая практика в реальном трейдинге. Следует опробовать MVO на другой платформе. Потом можно будет вложить деньги в оптимизированный портфель акций или одного из ETF, позволить платформе провести балансировку распределения средств на обычных интервалах, откатить, подождать и начать зарабатывать постепенно и вдумчиво.
Реализация MVO
Для реализации на Zorro автор берет раскладку Марковица из публикации 1959 года. В Главе 8 он описывает алгоритм MVO самым понятным и доступным способом. Для не самых продвинутых программистов здесь даже есть введение в линейную алгебру. Автор добавил к оригинальному алгоритму лишь ограничение по весу, как это предлагают сделать авторы вышеупомянутой статьи. В итоге оказалось, что это была отличная идея. Данное условие помогло стабилизировать алгоритм и улучшило его производительность за пределами выборки.
Предвкушая появление быстрых и умных вычислительных машин, Марковиц включил в описание набор примеров, по которым можно проверить, был ли алгоритм запрограммирован верно. Вот так выглядит эта проверка:
function main()
{
var Means[3] = { .062,.146,.128 };
var Covariances[3][3] = { .0146,.0187,.0145,.0187,.0854,.0104,.0145,.0104,.0289 };
var Weights[3];
var BestVariance = markowitz(Covariances,Means,3);
markowitzReturn(Weights,1);
printf("\nMax: %.2f %.2f %.2f",Weights[0],Weights[1],Weights[2]);
markowitzReturn(Weights,BestVariance);
printf("\nBest: %.2f %.2f %.2f",Weights[0],Weights[1],Weights[2]);
markowitzReturn(Weights,0);
printf("\nMin: %.2f %.2f %.2f",Weights[0],Weights[1],Weights[2]);
}
Здесь средние и ковариации выстроены в скрипт, взятый из набора примеров, предложенных Марковицем. Функция markowitz запускает алгоритм и возвращает значение отклонения, привязанное к лучшему коэффициенту Шарпа. Затем функция markowitzReturn рассчитывает весы (нагрузку) распределение капитала с максимальным возвратом среднего для предложенного отклонения. Значения весов для максимума, наилучшего и минимума отклонения выведены на печать. Если мы все сделали верно, эти значения должны совпадать с теми, что приведены в книге Марковица.
Max: 0.00 1.00 0.00 Best: 0.00 0.22 0.78 Min: 0.99 0.00 0.01
Выбор активов
Для долгосрочных портфелей вы не можете использовать инструменты Forex или CFD с высоким уровнем левереджа (плечом), которые годятся для краткосрочных стратегий. Вместо этого вы инвестируете в акции, ETF или другие похожие активы. Для алгоритмического трейдинга в них есть определенная польза:
- Исключается игра с нулевой суммой. На длинной дистанции акции и индексы ETF имеют положительное значение возврата к среднему, исходя из дивидендов и трендов рынка.
- Появляется больше надежных брокеров. Брокеров, работающих с акциями и ETF, регулируют, чего нельзя сказать про брокеров с Форекса и CFD.
- Больше данных для закачки в ваш алгоритм. Например, сведения об объемах и глубине рынка.
- Больше выбор активов в различных секторах рынка.
- Больше трейдинговых методов.
Очевидный недостаток этих инструментов – низкий уровень левереджа. Например, 1:4 вместо 1:100 на валютном рынке. Низкий левередж годится для долгосрочных инвестиций, но на нем нельзя заработать быстро. С долгосрочными портфелями связан еще ряд ограничений. MVO, очевидно, не сработает с вещами, у которых не будет положительного возврата среднего. Это не сработает, даже если доходы будут прочно коррелированны. Поэтому при выборе активов стоит обращать внимание не только на возвраты, но и на корреляцию. Вот пример скрипта Zorro для этой задачи:
#define NN 30 // max number of assets
function run()
{
BarPeriod = 1440;
NumYears = 7;
LookBack = NumBars;
string Names[NN];
vars Returns[NN];
var Correlations[NN][NN];
int N = 0;
while(Names[N] = loop(
"TLT","LQD","SPY","GLD","VGLT","AOK"))
{
if(is(INITRUN))
assetHistory(Names[N],FROM_YAHOO);
asset(Names[N]);
Returns[N] = series((priceClose(0)-priceClose(1))/priceClose(1));
if(N++ >= NN) break;
}
if(is(EXITRUN)) {
int i,j;
for(i=0; i<N; i++)
for(j=0; j<N; j++)
Correlations[N*i+j] =
Correlation(Returns[i],Returns[j],LookBack);
plotHeatmap("Correlation",Correlations,N,N);
for(i=0; i<N; i++)
printf("\n%i - %s: Mean %.2f%% Variance %.2f%%",
i+1,Names[i],
100*annual(Moment(Returns[i],LookBack,1)),
252*100*Moment(Returns[i],LookBack,2));
}
}
Для начала он устанавливает ряд параметров, затем запускает цикл с N активами. Здесь для примера даны самые популярные ETF. Есть сайт etfdb.com, который поможет вам заменить их на оптимальную комбинацию.
При первом запуске цены активов были скачены с Yahoo. Функция assetHistory сохраняет их в качестве исторических данных. Потом активы отбираются, подсчитываются их возвраты, и эти данные уже хранятся в сериях данных
Returns. Эта процедура повторяется на каждый день из 7 лет тестового периода (на практике все зависит от того, когда выбранные ETF активы становятся доступными). В итоге скрипт распечатывает ежегодные значения возврата среднего и отклонений каждого актива. Они становятся, соответственно, первым и вторым moment каждой из серий. Функция annual и множитель 252 конвертируют ежедневные значения в годовые. В нашем примере результат получился следующий:1 - TLT: Mean 10.75% Variance 2.29% 2 - LQD: Mean 6.46% Variance 0.31% 3 - SPY: Mean 13.51% Variance 2.51% 4 - GLD: Mean 3.25% Variance 3.04% 5 - VGLT: Mean 9.83% Variance 1.65% 6 - AOK: Mean 4.70% Variance 0.23%
Идеальный ETF будет иметь высокое значение возврата среднего, низкое отклонение и слабую корреляцию с другими активами в выборке. Корреляцию можно увидеть в корреляционной матрице, которая рассчитывается для всех собранных значений возвратов и рисуется в виде тепловой диаграммы N*N.
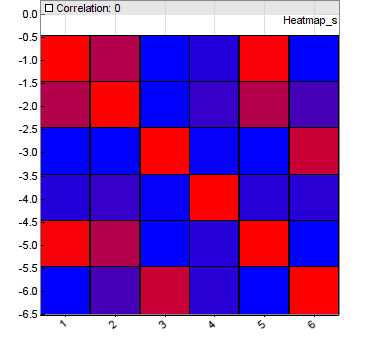
Матрица содержит корреляционный коэффициент каждого актива по отношению к каждому другому активу. В нашем случае их 6. Синий цвет – для слабой корреляции, красный, следовательно, для высокой. Из этой диаграммы видно, что некоторые активы не следовало выбирать.
Предел эффективности
После выбора активов в наш портфель, пришло время рассчитать оптимальное распределение капитала в нем через алгоритм MVO. При любом раскладе, «оптимальность» зависит от допущения рисков. Другими словами, волатильности портфеля. Для каждого из значений риска существует свое оптимальное распределение, которое генерирует максимальную прибыль. То есть оптимальное распределение – это не застывшая точка, а скорее кривая на графике возврат/отклонение. Ее еще называют предел или граница эффективности. Мы можем рассчитать ее и нарисовать в виде диаграммы, используя следующий скрипт:
function run()
{
... // similar to Heatmap script
if(is(EXITRUN)) {
int i,j;
for(i=0; i<N; i++) {
Means[i] = Moment(Returns[i],LookBack,1);
for(j=0; j<N; j++)
Covariances[N*i+j] =
Covariance(Returns[i],Returns[j],LookBack);
}
var BestV = markowitz(Covariances,Means,N);
var MinV = markowitzVariance(0,0);
var MaxV = markowitzVariance(0,1);
int Steps = 50;
for(i=0; i<Steps; i++) {
var V = MinV + i*(MaxV-MinV)/Steps;
var R = markowitzReturn(0,V);
plotBar("Frontier",i,V,100*R,LINE|LBL2,BLACK);
}
plotGraph("Max Sharpe",(BestV-MinV)*Steps/(MaxV-MinV),
100*markowitzReturn(0,BestV),SQUARE,GREEN);
}
}
Пропустим первую его часть, она идентична коду для создания теплокарты. Только в данном случае просчитывается матрица ковариаций. Ковариации и возвраты среднего заносятся в функцию
markowitz, которая снова делает возврат отклонения, исходя из лучшего коэффициента Шарпа. Тот в свою очередь обращается к markowitzVariance, происходит возврат высшего и низшего отклонения предела эффективности. Получаем границы графика. В итоге скрипт выдает 50 точек ежегодного возврата среднего от низшего до высшего отклонений: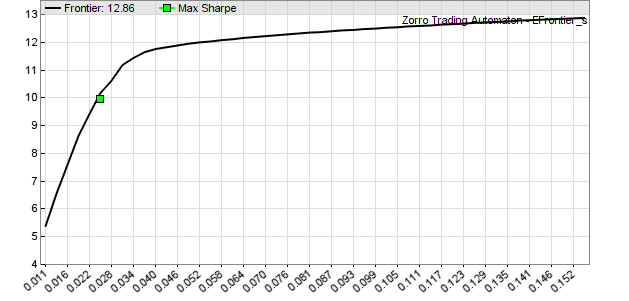
Справа мы можем видеть, как портфель достигает максимального ежегодного уровня прибыли в 12,9%. Слева имеем значение 5,4%, но с числом ежедневных отклонений меньше 10. Зеленая точка на графике обозначает лучший коэффициент Шарпа (прибыль деленная на корень квадратный отклонений) с 10% ежегодного дохода при отклонении 0,025. Это оптимальный портфель. По крайней мере, в ретроспективе данных.
Эксперимент
Как наш оптимизированный по среднему/отклонению портфель ведет себя в пределах выборки и за пределами выборки в сравнении с показателем 1/N? Ниже приведен скрипт для экспериментальной проверки с по-разному скомпонованными портфелями, периодами отката, ограничениями по весу и отклонениями:
#define DAYS 252 // 1 year lookback period
#define NN 30 // max number of assets
function run()
{
... // similar to Heatmap script
int i,j;
static var BestVariance = 0;
if(tdm() == 1 && !is(LOOKBACK)) {
for(i=0; i<N; i++) {
Means[i] = Moment(Returns[i],LookBack,1);
for(j=0; j<N; j++)
Covariances[N*i+j] = Covariance(Returns[i],Returns[j],LookBack);
}
BestVariance = markowitz(Covariances,Means,N,0.5);
}
var Weights[NN];
static var Return, ReturnN, ReturnMax, ReturnBest, ReturnMin;
if(is(LOOKBACK)) {
Month = 0;
ReturnN = ReturnMax = ReturnBest = ReturnMin = 0;
}
if(BestVariance > 0) {
for(Return=0,i=0; i<N; i++) Return += (Returns[i])[0]/N; // 1/N
ReturnN = (ReturnN+1)*(Return+1)-1;
markowitzReturn(Weights,0); // min variance
for(Return=0,i=0; i<N; i++) Return += Weights[i]*(Returns[i])[0];
ReturnMin = (ReturnMin+1)*(Return+1)-1;
markowitzReturn(Weights,1); // max return
for(Return=0,i=0; i<N; i++) Return += Weights[i]*(Returns[i])[0];
ReturnMax = (ReturnMax+1)*(Return+1)-1;
markowitzReturn(Weights,BestVariance); // max Sharpe
for(Return=0,i=0; i<N; i++) Return += Weights[i]*(Returns[i])[0];
ReturnBest = (ReturnBest+1)*(Return+1)-1;
plot("1/N",100*ReturnN,AXIS2,BLACK);
plot("Max Sharpe",100*ReturnBest,AXIS2,GREEN);
plot("Max Return",100*ReturnMax,AXIS2,RED);
plot("Min Variance",100*ReturnMin,AXIS2,BLUE);
}
}
Цикл проверки составляет 7 лет исторических данных. Он сохраняет ежедневные возвраты в сериях данных
Returns. В первый день трейдинга каждого месяца (tdm() == 1) подсчитываются матрицы средних и ковариаций за последние 252 дня. На их основании измеряется предел эффективности. В нашем случае ограничение по весу составляет 0,5 по отношению к точке минимального отклонения. Если взять за основу этот предел эффективности, то мы получаем ежедневную общую прибыль с одинаковым весом (ReturnN), лучшим коэффициентом Шарпа (ReturnBest), минимальным отклонением (ReturnMin) и максимальным доходом (ReturnMax). Вес остается неизменным до следующей балансировки, когда мы будем проходить тест за пределами выборки. Прибыли за 4 дня добавляется к 4 разным кривым акций: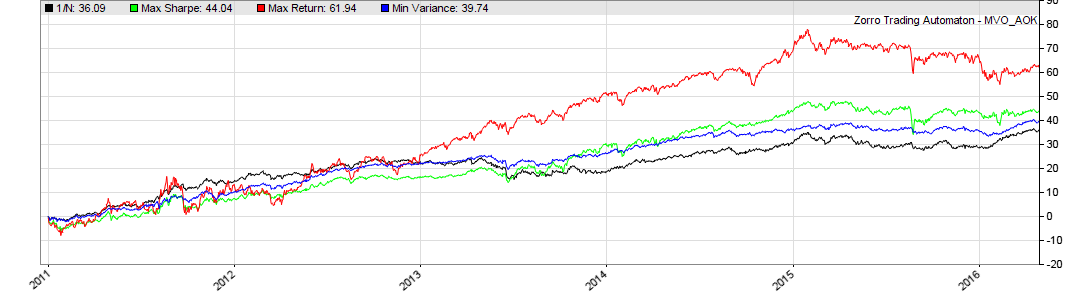
Из графика можно видеть, что MVO улучшил портфель для всех трех вариантов, несмотря на свою плохую репутацию. Черная линия отмечает 1/N портфеля с одинаковым весом для каждого актива. Синяя линия обозначает портфель с минимальным отклонением. Мы видим, что его отдача выше, чем 1/N, при гораздо меньшей волатильности. Красная линия – портфель с максимальной доходностью, но высокой волатильностью. Зеленая линия – лучший коэффициент Шарпа, это средний по всем показателям портфель. Состав портфеля может быть разный, но зеленая и синяя линии показывают наилучшие варианты.
Для проверки месячной балансировки распределения весов, можно отобразить их в виде тепловой карты.

Горизонтальная ось обозначает месячный период нашей симуляции. Вертикальная – номер актива. Высокие веса закрашены красным, нижние – синим. Это распределение весов для портфеля с максимальным коэффициентом Шарпа, состоящее из 6 активов ETF.
«Заносим» в систему деньги
После всех экспериментов можно кодировать долгосрочную систему. Для этого предлагается следующий порядок действий:
- Предел эффективности рассчитывается, исходя из ежедневной прибыли последний 252 трейдинговых дней. То есть одного года. Это лучший период, если верить статье, которую мы цитировали в начале. Так как большинство ETF демонстрируют годовой моментум.
- Балансировка портфеля производится раз в месяц. В тестах более короткие периоды показали свою бесполезность, и снизили доход из-за более высоких трейдинговых издержек. При более длинных периодах (3 месяца) работа системы ухудшается.
- Точку предела эффективности можно сделать плавающей в границах минимального отклонения и максимального коэффициента Шарпа. Так вы сможете контролировать уровень риска системы.
- Мы используем 50% ограничение по весу для минимального отклонения. Это не самый оптимальный портфель, но, опять же, в цитированной статье (и тесты автора это подтвердили), говорится, что это улучшает баланс за пределами выборки.
Вот так выглядит скрипт:
#define LEVERAGE 4 // 1:4 leverage
#define DAYS 252 // 1 year
#define NN 30 // max number of assets
function run()
{
BarPeriod = 1440;
LookBack = DAYS;
string Names[NN];
vars Returns[NN];
var Means[NN];
var Covariances[NN][NN];
var Weights[NN];
var TotalCapital = slider(1,1000,0,10000,"Capital","Total capital to distribute");
var VFactor = slider(2,10,0,100,"Risk","Variance factor");
int N = 0;
while(Names[N] = loop(
"TLT","LQD","SPY","GLD","VGLT","AOK"))
{
if(is(INITRUN))
assetHistory(Names[N],FROM_YAHOO);
asset(Names[N]);
Returns[N] = series((priceClose(0)-priceClose(1))/priceClose(1));
if(N++ >= NN) break;
}
if(is(EXITRUN)) {
int i,j;
for(i=0; i<N; i++) {
Means[i] = Moment(Returns[i],LookBack,1);
for(j=0; j<N; j++)
Covariances[N*i+j] = Covariance(Returns[i],Returns[j],LookBack);
}
var BestVariance = markowitz(Covariances,Means,N,0.5);
var MinVariance = markowitzReturn(0,0);
markowitzReturn(Weights,MinVariance+VFactor/100.*(BestVariance-MinVariance));
for(i=0; i<N; i++) {
asset(Names[i]);
MarginCost = priceClose()/LEVERAGE;
int Position = TotalCapital*Weights[i]/MarginCost;
printf("\n%s: %d Contracts at %.0f$",Names[i],Position,priceClose());
}
}
}
Сам скрипт только «советует», но не торгует. Для автоматизации процесса еще понадобится интегрировать торгового робота через API брокерской системы (например, у ITinvest такой интерфейс получил название SmartCOM). При этом, если позиции открываются и закрываются раз в месяц, а данные об акциях можно найти и в открытом доступе, то интеграция может быть и не нужна — нужно будет просто запускать его раз в месяц, и анализировать его вывод:
TLT: 0 Contracts at 129$ LQD: 0 Contracts at 120$ SPY: 3 Contracts at 206$ GLD: 16 Contracts at 124$ VGLT: 15 Contracts at 80$ AOK: 0 Contracts at 32$
Очевидно, что оптимальный портфель за этот месяц будет состоять из трех сделок по SPY, 16 по GLD и 15 VGLT. Теперь можно вручную открывать и закрывать позиции в своей брокерской платформе, пока портфель не будет соответствовать распечатанному списку. Левередж по умолчанию – 4. Но его можно поменять по желанию в начале скрипта (#define). Если хотите сделать так, чтобы скрипт самостоятельно торговал, замените команду printf командой для открытия и закрытия позиций.
MVO против OptimalF
MVO можно использовать не только для портфеля с определенным количеством активов, но и для разных трейдинговых систем. Автор блога Financial провел эксперимент, в ходе которого выяснилось, что MVO не превосходит результат, который можно получить при применении коэффициента OptimalF Ральфа Винса. Он используется в большинстве трейдинговых систем. OptimalF не осуществляет корреляции между компонентами, но учитывает глубину выборки средств. В то время как MVO работает только со средними и ковариациями. Идеальным решением было бы совместить оба подхода — но это дело будущих экспериментов.
Ссылки
- Momentum and Markowitz – A Golden Combination: Keller.Butler.Kipnis.2015
- Harry M. Markowitz, Portfolio Selection, Wiley 1959
Другие материалы по теме от ITinvest:
- Технологии фондового рынка: 10 заблуждений о нейронных сетях
Аналитические материалы о ситуации на финансовых рынках от экспертов ITinvest - Описание процесса создания архитектуры системы онлайн-трейдинга: подход аналитика хедж-фонда
- Как определить наилучшее время для сделки на фондовом рынке: Алгоритмы следования тренду
- ИБ-стартап Palantir поможет инвестбанку Credit Suisse создать систему для выявления недобросовестных трейдеров
- Эксперимент: Использование Google Trends для прогнозирования обвалов фондового рынка
- Эксперимент: создание алгоритма для прогнозирования поведения фондовых индексов
Поделиться с друзьями


achidutsu
Простите дилетанта ). А на каком языке и для какого терминала написаны скрипты? С уважением.
legik-9i
Насколько я понимаю, тут не важно на каком языке написанно. Мы просто исполняем код, где нам удобно, и получаем рекомендацию. Портфели, все таки, закупаются вручную
Возможно, я не прав. Ждём автора.