Некоторое время назад я натолкнулся на упражнение, которое выглядит не так уж и сложно:
Пусть последовательность xn определена так:
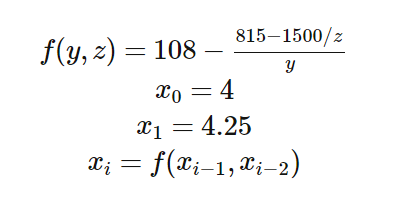
посчитайте x30.
Это не так уж и трудно закодировать, возможно реализовав xi как рекурсивную функцию. С обычными числами с плавающей запятой двойной точности, по мере увеличения i, результат красиво сходится к 100. Супер!
К сожалению, 100 даже близко не является правильным ответом. На самом деле последовательность сходится к 5.
Эта последовательность известна под именем «Рекуррентное соотношение Мюллера» и синтезирована специально для демонстрации того, как быстро и драматически ошибки округления чисел с плавающей запятой приводят к катастрофическим результатам, при правильных (ну, неправильных) условиях. В этой работе (pdf) в деталях рассматриваются различные опасности округления, в частности и эта последовательность (стр. 14). Другое описание проблемы можно увидеть здесь (pdf).
Думаю, что многие программисты, включая меня, осознают, что математика чисел с плавающей запятой может пойти не так в некоторых ситуациях, но отмахиваются от проблемы, считая, что это может произойти только если в вычислениях участвуют очень большие или очень маленькие числа, либо когда накапливается огромное число ошибок. Это упражнение с невинно выглядящими константами и небольшим количеством итераций прекрасно демонстрирует, что ошибки округления могут иметь существенное влияние даже помимо экстремальных чисел. В данном случае нестабильность неподвижной точки 5 приводит к тому, что даже небольшие ошибки значительно меняют результат.
Я больше ничего не могу добавить, но думаю, что этой проблемой стоит поделиться.
Мы можем сравнить первые сто значений последовательности между обычными числами с плавающей запятой и арифметикой с произвольной точностью с помощью короткой программы на Mathematica. Мы используем удобный синтакс мемоизации Mathematica, так что вычисления происходят довольно быстро даже для 100 и более итераций.
f[y_, z_] := 108 - (815 - 1500/z)/y;
xExact[0] = 4;
xExact[1] = 17/4;
xExact[n_] := xExact[n] = f[xExact[n-1], xExact[n-2]];
xFloat[0] = 4;
xFloat[1] = 4.25;
xFloat[n_] := xFloat[n] = f[xFloat[n-1], xFloat[n-2]];
TableForm[
Table[{i, N[xExact[i], 20], N[xFloat[i], 20]}, {i, 0, 100}],
TableHeadings ->
{None, {"i", "x[i] \"exact\"", "x[i] floating point"}}
Пусть последовательность xn определена так:
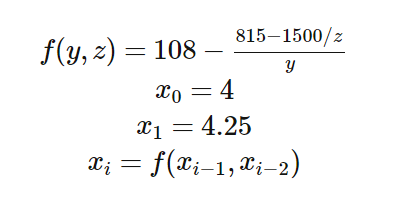
посчитайте x30.
Это не так уж и трудно закодировать, возможно реализовав xi как рекурсивную функцию. С обычными числами с плавающей запятой двойной точности, по мере увеличения i, результат красиво сходится к 100. Супер!
К сожалению, 100 даже близко не является правильным ответом. На самом деле последовательность сходится к 5.
Проблема
Эта последовательность известна под именем «Рекуррентное соотношение Мюллера» и синтезирована специально для демонстрации того, как быстро и драматически ошибки округления чисел с плавающей запятой приводят к катастрофическим результатам, при правильных (ну, неправильных) условиях. В этой работе (pdf) в деталях рассматриваются различные опасности округления, в частности и эта последовательность (стр. 14). Другое описание проблемы можно увидеть здесь (pdf).
Думаю, что многие программисты, включая меня, осознают, что математика чисел с плавающей запятой может пойти не так в некоторых ситуациях, но отмахиваются от проблемы, считая, что это может произойти только если в вычислениях участвуют очень большие или очень маленькие числа, либо когда накапливается огромное число ошибок. Это упражнение с невинно выглядящими константами и небольшим количеством итераций прекрасно демонстрирует, что ошибки округления могут иметь существенное влияние даже помимо экстремальных чисел. В данном случае нестабильность неподвижной точки 5 приводит к тому, что даже небольшие ошибки значительно меняют результат.
Я больше ничего не могу добавить, но думаю, что этой проблемой стоит поделиться.
Вычисление корректного результата
Мы можем сравнить первые сто значений последовательности между обычными числами с плавающей запятой и арифметикой с произвольной точностью с помощью короткой программы на Mathematica. Мы используем удобный синтакс мемоизации Mathematica, так что вычисления происходят довольно быстро даже для 100 и более итераций.
f[y_, z_] := 108 - (815 - 1500/z)/y;
xExact[0] = 4;
xExact[1] = 17/4;
xExact[n_] := xExact[n] = f[xExact[n-1], xExact[n-2]];
xFloat[0] = 4;
xFloat[1] = 4.25;
xFloat[n_] := xFloat[n] = f[xFloat[n-1], xFloat[n-2]];
TableForm[
Table[{i, N[xExact[i], 20], N[xFloat[i], 20]}, {i, 0, 100}],
TableHeadings ->
{None, {"i", "x[i] \"exact\"", "x[i] floating point"}}
Результаты:
i x[i] "exact" x[i] floating point ---------------------------------------------------- 0 4.0000000000000000000 4.0000000000000000000 1 4.2500000000000000000 4.25 2 4.4705882352941176471 4.47059 3 4.6447368421052631579 4.64474 4 4.7705382436260623229 4.77054 5 4.8557007125890736342 4.8557 6 4.9108474990827932004 4.91085 7 4.9455374041239167248 4.94554 8 4.9669625817627005987 4.96696 9 4.9800457013556311613 4.98004 10 4.9879794484783922601 4.98791 11 4.9927702880620680975 4.99136 12 4.9956558915066340266 4.96746 13 4.9973912683813441129 4.42971 14 4.9984339439448169190 -7.81676 15 4.9990600719708938678 168.943 16 4.9994359371468391480 102.04 17 4.9996615241037675378 100.1 18 4.9997969007134179127 100.005 19 4.9998781354779312492 100. 20 4.9999268795045999045 100. 21 4.9999561270611577381 100. 22 4.9999736760057124446 100. 23 4.9999842055202727079 100. 24 4.9999905232822276594 100. 25 4.9999943139585595936 100. 26 4.9999965883712560237 100. 27 4.9999979530213569080 100. 28 4.9999987718123113300 100. 29 4.9999992630872057846 100. 30 4.9999995578522583059 100. 31 4.9999997347113315242 100. 32 4.9999998408267904691 100. 33 4.9999999044960712411 100. 34 4.9999999426976416502 100. 35 4.9999999656185845961 100. 36 4.9999999793711506158 100. 37 4.9999999876226903184 100. 38 4.9999999925736141727 100. 39 4.9999999955441684970 100. 40 4.9999999973265010958 100. 41 4.9999999983959006566 100. 42 4.9999999990375403937 100. 43 4.9999999994225242361 100. 44 4.9999999996535145416 100. 45 4.9999999997921087250 100. 46 4.9999999998752652350 100. 47 4.9999999999251591410 100. 48 4.9999999999550954846 100. 49 4.9999999999730572908 100. 50 4.9999999999838343745 100. 51 4.9999999999903006247 100. 52 4.9999999999941803748 100. 53 4.9999999999965082249 100. 54 4.9999999999979049349 100. 55 4.9999999999987429610 100. 56 4.9999999999992457766 100. 57 4.9999999999995474659 100. 58 4.9999999999997284796 100. 59 4.9999999999998370877 100. 60 4.9999999999999022526 100. 61 4.9999999999999413516 100. 62 4.9999999999999648110 100. 63 4.9999999999999788866 100. 64 4.9999999999999873319 100. 65 4.9999999999999923992 100. 66 4.9999999999999954395 100. 67 4.9999999999999972637 100. 68 4.9999999999999983582 100. 69 4.9999999999999990149 100. 70 4.9999999999999994090 100. 71 4.9999999999999996454 100. 72 4.9999999999999997872 100. 73 4.9999999999999998723 100. 74 4.9999999999999999234 100. 75 4.9999999999999999540 100. 76 4.9999999999999999724 100. 77 4.9999999999999999835 100. 78 4.9999999999999999901 100. 79 4.9999999999999999940 100. 80 4.9999999999999999964 100. 81 4.9999999999999999979 100. 82 4.9999999999999999987 100. 83 4.9999999999999999992 100. 84 4.9999999999999999995 100. 85 4.9999999999999999997 100. 86 4.9999999999999999998 100. 87 4.9999999999999999999 100. 88 4.9999999999999999999 100. 89 5.0000000000000000000 100. 90 5.0000000000000000000 100. 91 5.0000000000000000000 100. 92 5.0000000000000000000 100. 93 5.0000000000000000000 100. 94 5.0000000000000000000 100. 95 5.0000000000000000000 100. 96 5.0000000000000000000 100. 97 5.0000000000000000000 100. 98 5.0000000000000000000 100. 99 5.0000000000000000000 100. 100 5.0000000000000000000 100.

