ГОСТ Р 34.12 '15 на SSE2, или Не так уж и плох Кузнечик / forpes.ru

Главная
ГОСТ Р 34.12 '15 на SSE2, или Не так уж и плох Кузнечик

ГОСТ Р 34.12 '15 на SSE2, или Не так уж и плох Кузнечик +51

11.10.2016 16:38

aaprelev 41 10600 Источник

На Хабре уже как минимум дважды упоминался новый отечественный стандарт блочного шифрования ГОСТ Р 34.12 2015 «Кузнечик», ru_crypt в своем посте рассмотрел основные механизмы и преобразования нового стандарта, а sebastian_mg занимался пошаговой трассировкой базового преобразования. Но многие вопросы остались без ответа. Насколько быстр новый ГОСТ? Можно ли его оптимизировать, эффективно реализовать, ускорить аппаратно?

О стандарте ГОСТ Р 34.12 '15

Приказом от 19 июня 2015 года №749 в качестве нового стандарта блочного шифрования утвержден ГОСТ Р 34.12 2015. Стандарт разработан Центром защиты информации и специальной связи ФСБ России с участием ОАО «ИнфоТеКС», внесен Техническим комитетом по стандартизации ТК 26 «Криптографическая защита информации», и вступил в действие с 1 января 2016 года.

Официальное pdf-издание стандарта качаем здесь, а эталонную реализацию — здесь (обе ссылки ведут на официальный сайт ТК 26).

Этот стандарт содержит описания двух блочных шифров: «Магмы» с длиной блока в 64 бита и «Кузнечика» с длиной блока в 128 бит; при этом «Магма» — всего лишь новое название для старого, всем хорошо известного блочного шифра ГОСТ 28147 '89 (на самом деле, не совсем новое, именно под этим кодовым названием разрабатывался прежний стандарт блочного шифрования вплоть до 1994 года) с зафиксированными узлами замены. «Наконец–то, история нас чему–то научила», — скажете вы, и будете правы.

В этой статье пойдет речь про другой шифр, имеющий длину блока 128 бит, и носящий кодовое имя «Кузнечик». По городской ленде, имя шифра вовсе не связано с зеленым насекомым, а образовано первыми слогами фамилий авторов этого шифра: Кузьмин, Нечаев и компания.

Описание «Кузнечика»

Отличия «Кузнечика» от «Магмы»

Новый шифр существенно отличается от старого, среди его основных достоинств можно выделить

вдвое увеличенную длину блока (128 бит, или 16 байт, против ~~64 бит, или 8 байт~~),
нетривиальное ключевое расписание (сеть Фейстеля как ключевое расписание против ~~использования частей секретного ключа в качестве цикловых ключей~~),
сокращенное число циклов (10 циклов против ~~32 циклов~~),
принципиально иное устройство самого шифра (LSX-шифр против ~~сети Фейстеля~~).

Базовое преобразование

Шифр принадлежит к классу LSX-шифров: его базовое преобразование (функция шифрования блока) представляется десятью циклами последовательных преобразований L (линейное преобразование), S (подстановка) и X (смешивание с цикловым ключом):

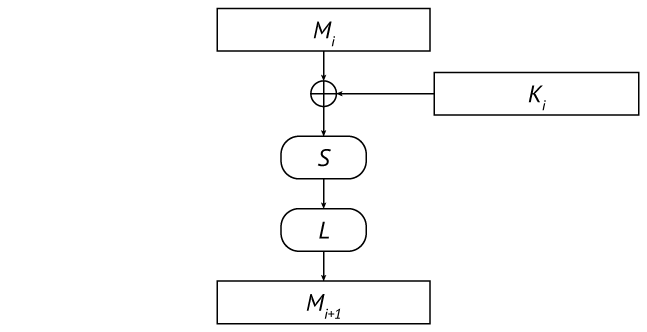
Полный цикл базового преобразования

Алгебраически шифртекст C зависит от открытого текста P следующим образом:

$C = X_{9} \circ LSX_{8} \circ \dots \circ LSX_{0} \left( P \right),$

то есть за девятью полными циклами следует последний неполный (только смешивание с ключом). Преобразование X смешивает промежуточный текст очередного цикла с соответствующим цикловым ключом простым сложением по модулю 2:

$X(M_i) = M_i \oplus K_i.$

Преобразование S применяет одну и ту же фиксированную подстановку $\pi$ к каждому байту промежуточного текста:

$S(M_i) = \overline{\pi(m_0) \pi(m_1) \dots \pi(m_{15})}, \text{ где } \pi \colon \mathbb{Z}_2^8 \mapsto \mathbb{Z}_2^8 \text{ и } M_i = \overline{m_0 m_1 \dots m_{15}}.$

Преобразование L представимо линейной формой над полем GF(256), построенным с помощью неприводимого многочлена

$p(x) = x^8 + x^7 + x^6 + x + 1,$

и сводится к умножению вектора–строки промежуточного текста на некоторую матрицу над этим полем (каждый байт текста и матрицы является многочленом поля, представленным своими коэффициентами):

$L(M_i) = M_i \times M_{16 \times 16}.$

Пример кода базового преобразования

/* Применяет S-преобразование к блоку. */
static void 
applySTransformation(
        uint8_t *block
) {
    for (int byteIndex = 0; byteIndex < BlockLengthInBytes; byteIndex += 8) {
        block[byteIndex + 0] = Pi[block[byteIndex + 0]];
        block[byteIndex + 1] = Pi[block[byteIndex + 1]];
        block[byteIndex + 2] = Pi[block[byteIndex + 2]];
        block[byteIndex + 3] = Pi[block[byteIndex + 3]];

        block[byteIndex + 4] = Pi[block[byteIndex + 4]];
        block[byteIndex + 5] = Pi[block[byteIndex + 5]];
        block[byteIndex + 6] = Pi[block[byteIndex + 6]];
        block[byteIndex + 7] = Pi[block[byteIndex + 7]];
    }
}

/* Применяет L-преобразование к блоку. */
static void 
applyLTransformation(
        const uint8_t *input,
        uint8_t *output
) {
    for (int byteIndex = 0; byteIndex < BlockLengthInBytes; ++byteIndex) {
        uint8_t cache = 0;

        for (int addendIndex = 0; addendIndex < BlockLengthInBytes; ++addendIndex) {
            cache ^= multiplyInGF256(LTransformationMatrix[addendIndex][byteIndex], 
                                     input[addendIndex]);
        }

        output[byteIndex] = cache;
    }
}

/* Полный цикл шифрования блока. */
static void 
applyXSLTransformation(
        const uint8_t *key,
        uint8_t *block,
        uint8_t *temporary
) {
    applyXTransformation(key, block, temporary);
    applySTransformation(temporary);
    applyLTransformation(temporary, block);
}

/* Базовое преобразование (шифрование блока). */
void 
encryptBlock(
        uint8_t *restrict block,
        const uint8_t *restrict roundKeys
) {
    uint8_t cache[BlockLengthInBytes] = {0};
    int round = 0;
    for (; round < NumberOfRounds - 1; ++round) {
        applyXSLTransformation(&roundKeys[BlockLengthInBytes * round], block, cache);
    }
    applyXTransformation(&roundKeys[BlockLengthInBytes * round], block, block);
}

Вычисленные матрица преобразования L и обратная к ней в C-friendly виде

/* Матрица преобразования L. */
const uint8_t LTransformationMatrix[16][16] = {
    0xcf, 0x6e, 0xa2, 0x76, 0x72, 0x6c, 0x48, 0x7a, 0xb8, 0x5d, 0x27, 0xbd, 0x10, 0xdd, 0x84, 0x94,
    0x98, 0x20, 0xc8, 0x33, 0xf2, 0x76, 0xd5, 0xe6, 0x49, 0xd4, 0x9f, 0x95, 0xe9, 0x99, 0x2d, 0x20,
    0x74, 0xc6, 0x87, 0x10, 0x6b, 0xec, 0x62, 0x4e, 0x87, 0xb8, 0xbe, 0x5e, 0xd0, 0x75, 0x74, 0x85,
    0xbf, 0xda, 0x70, 0x0c, 0xca, 0x0c, 0x17, 0x1a, 0x14, 0x2f, 0x68, 0x30, 0xd9, 0xca, 0x96, 0x10,
    0x93, 0x90, 0x68, 0x1c, 0x20, 0xc5, 0x06, 0xbb, 0xcb, 0x8d, 0x1a, 0xe9, 0xf3, 0x97, 0x5d, 0xc2,
    0x8e, 0x48, 0x43, 0x11, 0xeb, 0xbc, 0x2d, 0x2e, 0x8d, 0x12, 0x7c, 0x60, 0x94, 0x44, 0x77, 0xc0,
    0xf2, 0x89, 0x1c, 0xd6, 0x02, 0xaf, 0xc4, 0xf1, 0xab, 0xee, 0xad, 0xbf, 0x3d, 0x5a, 0x6f, 0x01,
    0xf3, 0x9c, 0x2b, 0x6a, 0xa4, 0x6e, 0xe7, 0xbe, 0x49, 0xf6, 0xc9, 0x10, 0xaf, 0xe0, 0xde, 0xfb,
    0x0a, 0xc1, 0xa1, 0xa6, 0x8d, 0xa3, 0xd5, 0xd4, 0x09, 0x08, 0x84, 0xef, 0x7b, 0x30, 0x54, 0x01,
    0xbf, 0x64, 0x63, 0xd7, 0xd4, 0xe1, 0xeb, 0xaf, 0x6c, 0x54, 0x2f, 0x39, 0xff, 0xa6, 0xb4, 0xc0,
    0xf6, 0xb8, 0x30, 0xf6, 0xc4, 0x90, 0x99, 0x37, 0x2a, 0x0f, 0xeb, 0xec, 0x64, 0x31, 0x8d, 0xc2,
    0xa9, 0x2d, 0x6b, 0x49, 0x01, 0x58, 0x78, 0xb1, 0x01, 0xf3, 0xfe, 0x91, 0x91, 0xd3, 0xd1, 0x10,
    0xea, 0x86, 0x9f, 0x07, 0x65, 0x0e, 0x52, 0xd4, 0x60, 0x98, 0xc6, 0x7f, 0x52, 0xdf, 0x44, 0x85,
    0x8e, 0x44, 0x30, 0x14, 0xdd, 0x02, 0xf5, 0x2a, 0x8e, 0xc8, 0x48, 0x48, 0xf8, 0x48, 0x3c, 0x20,
    0x4d, 0xd0, 0xe3, 0xe8, 0x4c, 0xc3, 0x16, 0x6e, 0x4b, 0x7f, 0xa2, 0x89, 0x0d, 0x64, 0xa5, 0x94,
    0x6e, 0xa2, 0x76, 0x72, 0x6c, 0x48, 0x7a, 0xb8, 0x5d, 0x27, 0xbd, 0x10, 0xdd, 0x84, 0x94, 0x01,
};

/* Матрица, обратная к матрице преобразования L. */
const uint8_t inversedLTransformationMatrix[16][16] = {
    0x01, 0x94, 0x84, 0xdd, 0x10, 0xbd, 0x27, 0x5d, 0xb8, 0x7a, 0x48, 0x6c, 0x72, 0x76, 0xa2, 0x6e,
    0x94, 0xa5, 0x64, 0x0d, 0x89, 0xa2, 0x7f, 0x4b, 0x6e, 0x16, 0xc3, 0x4c, 0xe8, 0xe3, 0xd0, 0x4d,
    0x20, 0x3c, 0x48, 0xf8, 0x48, 0x48, 0xc8, 0x8e, 0x2a, 0xf5, 0x02, 0xdd, 0x14, 0x30, 0x44, 0x8e,
    0x85, 0x44, 0xdf, 0x52, 0x7f, 0xc6, 0x98, 0x60, 0xd4, 0x52, 0x0e, 0x65, 0x07, 0x9f, 0x86, 0xea,
    0x10, 0xd1, 0xd3, 0x91, 0x91, 0xfe, 0xf3, 0x01, 0xb1, 0x78, 0x58, 0x01, 0x49, 0x6b, 0x2d, 0xa9,
    0xc2, 0x8d, 0x31, 0x64, 0xec, 0xeb, 0x0f, 0x2a, 0x37, 0x99, 0x90, 0xc4, 0xf6, 0x30, 0xb8, 0xf6,
    0xc0, 0xb4, 0xa6, 0xff, 0x39, 0x2f, 0x54, 0x6c, 0xaf, 0xeb, 0xe1, 0xd4, 0xd7, 0x63, 0x64, 0xbf,
    0x01, 0x54, 0x30, 0x7b, 0xef, 0x84, 0x08, 0x09, 0xd4, 0xd5, 0xa3, 0x8d, 0xa6, 0xa1, 0xc1, 0x0a,
    0xfb, 0xde, 0xe0, 0xaf, 0x10, 0xc9, 0xf6, 0x49, 0xbe, 0xe7, 0x6e, 0xa4, 0x6a, 0x2b, 0x9c, 0xf3,
    0x01, 0x6f, 0x5a, 0x3d, 0xbf, 0xad, 0xee, 0xab, 0xf1, 0xc4, 0xaf, 0x02, 0xd6, 0x1c, 0x89, 0xf2,
    0xc0, 0x77, 0x44, 0x94, 0x60, 0x7c, 0x12, 0x8d, 0x2e, 0x2d, 0xbc, 0xeb, 0x11, 0x43, 0x48, 0x8e,
    0xc2, 0x5d, 0x97, 0xf3, 0xe9, 0x1a, 0x8d, 0xcb, 0xbb, 0x06, 0xc5, 0x20, 0x1c, 0x68, 0x90, 0x93,
    0x10, 0x96, 0xca, 0xd9, 0x30, 0x68, 0x2f, 0x14, 0x1a, 0x17, 0x0c, 0xca, 0x0c, 0x70, 0xda, 0xbf,
    0x85, 0x74, 0x75, 0xd0, 0x5e, 0xbe, 0xb8, 0x87, 0x4e, 0x62, 0xec, 0x6b, 0x10, 0x87, 0xc6, 0x74,
    0x20, 0x2d, 0x99, 0xe9, 0x95, 0x9f, 0xd4, 0x49, 0xe6, 0xd5, 0x76, 0xf2, 0x33, 0xc8, 0x20, 0x98,
    0x94, 0x84, 0xdd, 0x10, 0xbd, 0x27, 0x5d, 0xb8, 0x7a, 0x48, 0x6c, 0x72, 0x76, 0xa2, 0x6e, 0xcf,
};

Ключевое расписание

Действительно, многие ошибки, допущенные при разработке старшего шифра, были исправлены, в том числе уязвимое ключевое расписание. Напомню читателю, что в шифре ГОСТ 28147 '89 в качестве цикловых ключей использовались восемь 32-битных частей 256-битного секретного ключа в прямом порядке на циклах шифрования с первого по восьмой, с девятого по шестнадцатый, с семнадцатого по двадцать четвертый; и в обратном порядке на циклах с двадцать пятого по тридцать второй:

$K_0, K_1, \dots, K_6, K_7,\K_0, K_1, \dots, K_6, K_7,\K_0, K_1, \dots, K_6, K_7,\K_7, K_6, \dots, K_1, K_0.\\$

И именно такое слабое ключевое расписание позволило осуществить атаку с отражением на полный ГОСТ, снизив его стойкость с 256 бит до 225 бит (при любых узлах замены, с 2^32 материала на одном ключе; почитать про эту атаку можно здесь).

В новом стандарте выработка цикловых ключей осуществляется по схеме Фейстеля, при этом первыми двумя цикловыми ключами являются половины 256-битного секретного ключа, а каждая следующая пара цикловых ключей получается в результате применения восьми циклов преобразования Фейстеля к предыдущей паре цикловых ключей, где в качестве цикловой функции используется то же LSX преобразование, что и в базовом преобразовании, а в качестве цикловых ключей в схеме используется фиксированный набор констант:

$\left( K_{2i + 1}, K_{2i + 2} \right) = F^8 \left( K_{2i - 1}, K_{2i} \right); \text{ где } F \left( x, y \right) = \left( LSX_i(y) \oplus x, y \right).$

Пример кода, реализующего такое ключевое расписание

/* Вырабатывает цикловые ключи для шифрования по ГОСТ Р 34.12 '15. */
static void 
scheduleRoundKeys(
        uint8_t *restrict roundKeys,
        const void *restrict key,
        uint8_t *restrict memory
) {
    /* Копирование первой пары цикловых ключей. */
    memcpy(&roundKeys[0], key, BlockLengthInBytes * 2);

    for (int nextKeyIndex = 2, constantIndex = 0;
         nextKeyIndex != NumberOfRounds;
         nextKeyIndex += 2) {

        /* Копирование предыдущей пары цикловых ключей. */
        memcpy(&roundKeys[BlockLengthInBytes * (nextKeyIndex)],
               &roundKeys[BlockLengthInBytes * (nextKeyIndex - 2)],
               BlockLengthInBytes * 2);

        /* Применение преобразований Фейстеля. */
        for (int feistelRoundIndex = 0; 
             feistelRoundIndex < NumberOfRoundsInKeySchedule; 
             ++feistelRoundIndex) {
            applyFTransformation(&roundConstants[BlockLengthInBytes * constantIndex++],
                                 &roundKeys[BlockLengthInBytes * (nextKeyIndex)],
                                 &roundKeys[BlockLengthInBytes * (nextKeyIndex + 1)],
                                 &memory[0],
                                 &memory[BlockLengthInBytes]);
        }
    }
}

Примечания
256 бит вспомогательной памяти для циклового преобразования здесь передаются по указателю memory, но их можно выделять и на стеке.
Явная индексация массива с цикловыми ключами roundKeys произведена для наглядности и простоты, и может быть легко заменена на арифметику указателей.
Функция applyFTransformation применяет цикловое преобразование к полублокам схемы и производит своп этих полублоков, например, так:

/* Применяет цикловое преобразование схемы Фейстеля ключевого расписания. */
static void 
applyFTransformation(
        const uint8_t *restrict key,
        uint8_t *restrict left,
        uint8_t *restrict right,
        uint8_t *restrict temporary1,
        uint8_t *restrict temporary2
) {
    memcpy(temporary1, left, BlockLengthInBytes);
    applyXSLTransformation(key, temporary1, temporary2);
    applyXTransformation(temporary1, right, right);
    swapBlocks(left, right, temporary2);
}

Вычисленные цикловые ключи в ключевом расписании в C-friendly виде

const uint8_t roundConstants[512] = {
    0x6e, 0xa2, 0x76, 0x72, 0x6c, 0x48, 0x7a, 0xb8, 0x5d, 0x27, 0xbd, 0x10, 0xdd, 0x84, 0x94, 0x01,
    0xdc, 0x87, 0xec, 0xe4, 0xd8, 0x90, 0xf4, 0xb3, 0xba, 0x4e, 0xb9, 0x20, 0x79, 0xcb, 0xeb, 0x02,
    0xb2, 0x25, 0x9a, 0x96, 0xb4, 0xd8, 0x8e, 0x0b, 0xe7, 0x69, 0x04, 0x30, 0xa4, 0x4f, 0x7f, 0x03,
    0x7b, 0xcd, 0x1b, 0x0b, 0x73, 0xe3, 0x2b, 0xa5, 0xb7, 0x9c, 0xb1, 0x40, 0xf2, 0x55, 0x15, 0x04,
    0x15, 0x6f, 0x6d, 0x79, 0x1f, 0xab, 0x51, 0x1d, 0xea, 0xbb, 0x0c, 0x50, 0x2f, 0xd1, 0x81, 0x05,
    0xa7, 0x4a, 0xf7, 0xef, 0xab, 0x73, 0xdf, 0x16, 0x0d, 0xd2, 0x08, 0x60, 0x8b, 0x9e, 0xfe, 0x06,
    0xc9, 0xe8, 0x81, 0x9d, 0xc7, 0x3b, 0xa5, 0xae, 0x50, 0xf5, 0xb5, 0x70, 0x56, 0x1a, 0x6a, 0x07,
    0xf6, 0x59, 0x36, 0x16, 0xe6, 0x05, 0x56, 0x89, 0xad, 0xfb, 0xa1, 0x80, 0x27, 0xaa, 0x2a, 0x08,
    0x98, 0xfb, 0x40, 0x64, 0x8a, 0x4d, 0x2c, 0x31, 0xf0, 0xdc, 0x1c, 0x90, 0xfa, 0x2e, 0xbe, 0x09,
    0x2a, 0xde, 0xda, 0xf2, 0x3e, 0x95, 0xa2, 0x3a, 0x17, 0xb5, 0x18, 0xa0, 0x5e, 0x61, 0xc1, 0x0a,
    0x44, 0x7c, 0xac, 0x80, 0x52, 0xdd, 0xd8, 0x82, 0x4a, 0x92, 0xa5, 0xb0, 0x83, 0xe5, 0x55, 0x0b,
    0x8d, 0x94, 0x2d, 0x1d, 0x95, 0xe6, 0x7d, 0x2c, 0x1a, 0x67, 0x10, 0xc0, 0xd5, 0xff, 0x3f, 0x0c,
    0xe3, 0x36, 0x5b, 0x6f, 0xf9, 0xae, 0x07, 0x94, 0x47, 0x40, 0xad, 0xd0, 0x08, 0x7b, 0xab, 0x0d,
    0x51, 0x13, 0xc1, 0xf9, 0x4d, 0x76, 0x89, 0x9f, 0xa0, 0x29, 0xa9, 0xe0, 0xac, 0x34, 0xd4, 0x0e,
    0x3f, 0xb1, 0xb7, 0x8b, 0x21, 0x3e, 0xf3, 0x27, 0xfd, 0x0e, 0x14, 0xf0, 0x71, 0xb0, 0x40, 0x0f,
    0x2f, 0xb2, 0x6c, 0x2c, 0x0f, 0x0a, 0xac, 0xd1, 0x99, 0x35, 0x81, 0xc3, 0x4e, 0x97, 0x54, 0x10,
    0x41, 0x10, 0x1a, 0x5e, 0x63, 0x42, 0xd6, 0x69, 0xc4, 0x12, 0x3c, 0xd3, 0x93, 0x13, 0xc0, 0x11,
    0xf3, 0x35, 0x80, 0xc8, 0xd7, 0x9a, 0x58, 0x62, 0x23, 0x7b, 0x38, 0xe3, 0x37, 0x5c, 0xbf, 0x12,
    0x9d, 0x97, 0xf6, 0xba, 0xbb, 0xd2, 0x22, 0xda, 0x7e, 0x5c, 0x85, 0xf3, 0xea, 0xd8, 0x2b, 0x13,
    0x54, 0x7f, 0x77, 0x27, 0x7c, 0xe9, 0x87, 0x74, 0x2e, 0xa9, 0x30, 0x83, 0xbc, 0xc2, 0x41, 0x14,
    0x3a, 0xdd, 0x01, 0x55, 0x10, 0xa1, 0xfd, 0xcc, 0x73, 0x8e, 0x8d, 0x93, 0x61, 0x46, 0xd5, 0x15,
    0x88, 0xf8, 0x9b, 0xc3, 0xa4, 0x79, 0x73, 0xc7, 0x94, 0xe7, 0x89, 0xa3, 0xc5, 0x09, 0xaa, 0x16,
    0xe6, 0x5a, 0xed, 0xb1, 0xc8, 0x31, 0x09, 0x7f, 0xc9, 0xc0, 0x34, 0xb3, 0x18, 0x8d, 0x3e, 0x17,
    0xd9, 0xeb, 0x5a, 0x3a, 0xe9, 0x0f, 0xfa, 0x58, 0x34, 0xce, 0x20, 0x43, 0x69, 0x3d, 0x7e, 0x18,
    0xb7, 0x49, 0x2c, 0x48, 0x85, 0x47, 0x80, 0xe0, 0x69, 0xe9, 0x9d, 0x53, 0xb4, 0xb9, 0xea, 0x19,
    0x05, 0x6c, 0xb6, 0xde, 0x31, 0x9f, 0x0e, 0xeb, 0x8e, 0x80, 0x99, 0x63, 0x10, 0xf6, 0x95, 0x1a,
    0x6b, 0xce, 0xc0, 0xac, 0x5d, 0xd7, 0x74, 0x53, 0xd3, 0xa7, 0x24, 0x73, 0xcd, 0x72, 0x01, 0x1b,
    0xa2, 0x26, 0x41, 0x31, 0x9a, 0xec, 0xd1, 0xfd, 0x83, 0x52, 0x91, 0x03, 0x9b, 0x68, 0x6b, 0x1c,
    0xcc, 0x84, 0x37, 0x43, 0xf6, 0xa4, 0xab, 0x45, 0xde, 0x75, 0x2c, 0x13, 0x46, 0xec, 0xff, 0x1d,
    0x7e, 0xa1, 0xad, 0xd5, 0x42, 0x7c, 0x25, 0x4e, 0x39, 0x1c, 0x28, 0x23, 0xe2, 0xa3, 0x80, 0x1e,
    0x10, 0x03, 0xdb, 0xa7, 0x2e, 0x34, 0x5f, 0xf6, 0x64, 0x3b, 0x95, 0x33, 0x3f, 0x27, 0x14, 0x1f,
    0x5e, 0xa7, 0xd8, 0x58, 0x1e, 0x14, 0x9b, 0x61, 0xf1, 0x6a, 0xc1, 0x45, 0x9c, 0xed, 0xa8, 0x20,
};

Устройство узла замены

В стандарте узел замены задан таблицей значений; разработчики шифра утверждают, что эта таблица получена в результате перебора случайных таблиц значений с учетом требований к линейным и разностным свойствам.

Слой подстановок, S-преобразование

Узел замены и обратный к нему в C-friendly виде

/* Узел замены pi стандарта шифрования ГОСТ 34.12 Р 2015. */
const uint8_t Pi[256] = {
    0xfc, 0xee, 0xdd, 0x11, 0xcf, 0x6e, 0x31, 0x16, 0xfb, 0xc4, 0xfa, 0xda, 0x23, 0xc5, 0x04, 0x4d,
    0xe9, 0x77, 0xf0, 0xdb, 0x93, 0x2e, 0x99, 0xba, 0x17, 0x36, 0xf1, 0xbb, 0x14, 0xcd, 0x5f, 0xc1,
    0xf9, 0x18, 0x65, 0x5a, 0xe2, 0x5c, 0xef, 0x21, 0x81, 0x1c, 0x3c, 0x42, 0x8b, 0x01, 0x8e, 0x4f,
    0x05, 0x84, 0x02, 0xae, 0xe3, 0x6a, 0x8f, 0xa0, 0x06, 0x0b, 0xed, 0x98, 0x7f, 0xd4, 0xd3, 0x1f,
    0xeb, 0x34, 0x2c, 0x51, 0xea, 0xc8, 0x48, 0xab, 0xf2, 0x2a, 0x68, 0xa2, 0xfd, 0x3a, 0xce, 0xcc,
    0xb5, 0x70, 0x0e, 0x56, 0x08, 0x0c, 0x76, 0x12, 0xbf, 0x72, 0x13, 0x47, 0x9c, 0xb7, 0x5d, 0x87,
    0x15, 0xa1, 0x96, 0x29, 0x10, 0x7b, 0x9a, 0xc7, 0xf3, 0x91, 0x78, 0x6f, 0x9d, 0x9e, 0xb2, 0xb1,
    0x32, 0x75, 0x19, 0x3d, 0xff, 0x35, 0x8a, 0x7e, 0x6d, 0x54, 0xc6, 0x80, 0xc3, 0xbd, 0x0d, 0x57,
    0xdf, 0xf5, 0x24, 0xa9, 0x3e, 0xa8, 0x43, 0xc9, 0xd7, 0x79, 0xd6, 0xf6, 0x7c, 0x22, 0xb9, 0x03,
    0xe0, 0x0f, 0xec, 0xde, 0x7a, 0x94, 0xb0, 0xbc, 0xdc, 0xe8, 0x28, 0x50, 0x4e, 0x33, 0x0a, 0x4a,
    0xa7, 0x97, 0x60, 0x73, 0x1e, 0x00, 0x62, 0x44, 0x1a, 0xb8, 0x38, 0x82, 0x64, 0x9f, 0x26, 0x41,
    0xad, 0x45, 0x46, 0x92, 0x27, 0x5e, 0x55, 0x2f, 0x8c, 0xa3, 0xa5, 0x7d, 0x69, 0xd5, 0x95, 0x3b,
    0x07, 0x58, 0xb3, 0x40, 0x86, 0xac, 0x1d, 0xf7, 0x30, 0x37, 0x6b, 0xe4, 0x88, 0xd9, 0xe7, 0x89,
    0xe1, 0x1b, 0x83, 0x49, 0x4c, 0x3f, 0xf8, 0xfe, 0x8d, 0x53, 0xaa, 0x90, 0xca, 0xd8, 0x85, 0x61,
    0x20, 0x71, 0x67, 0xa4, 0x2d, 0x2b, 0x09, 0x5b, 0xcb, 0x9b, 0x25, 0xd0, 0xbe, 0xe5, 0x6c, 0x52,
    0x59, 0xa6, 0x74, 0xd2, 0xe6, 0xf4, 0xb4, 0xc0, 0xd1, 0x66, 0xaf, 0xc2, 0x39, 0x4b, 0x63, 0xb6,
};

/* Узел замены, обратный к pi, стандарта шифрования ГОСТ 34.12 Р 2015. */
const uint8_t InversedPi[256] = {
    0xa5, 0x2d, 0x32, 0x8f, 0x0e, 0x30, 0x38, 0xc0, 0x54, 0xe6, 0x9e, 0x39, 0x55, 0x7e, 0x52, 0x91,
    0x64, 0x03, 0x57, 0x5a, 0x1c, 0x60, 0x07, 0x18, 0x21, 0x72, 0xa8, 0xd1, 0x29, 0xc6, 0xa4, 0x3f,
    0xe0, 0x27, 0x8d, 0x0c, 0x82, 0xea, 0xae, 0xb4, 0x9a, 0x63, 0x49, 0xe5, 0x42, 0xe4, 0x15, 0xb7,
    0xc8, 0x06, 0x70, 0x9d, 0x41, 0x75, 0x19, 0xc9, 0xaa, 0xfc, 0x4d, 0xbf, 0x2a, 0x73, 0x84, 0xd5,
    0xc3, 0xaf, 0x2b, 0x86, 0xa7, 0xb1, 0xb2, 0x5b, 0x46, 0xd3, 0x9f, 0xfd, 0xd4, 0x0f, 0x9c, 0x2f,
    0x9b, 0x43, 0xef, 0xd9, 0x79, 0xb6, 0x53, 0x7f, 0xc1, 0xf0, 0x23, 0xe7, 0x25, 0x5e, 0xb5, 0x1e,
    0xa2, 0xdf, 0xa6, 0xfe, 0xac, 0x22, 0xf9, 0xe2, 0x4a, 0xbc, 0x35, 0xca, 0xee, 0x78, 0x05, 0x6b,
    0x51, 0xe1, 0x59, 0xa3, 0xf2, 0x71, 0x56, 0x11, 0x6a, 0x89, 0x94, 0x65, 0x8c, 0xbb, 0x77, 0x3c,
    0x7b, 0x28, 0xab, 0xd2, 0x31, 0xde, 0xc4, 0x5f, 0xcc, 0xcf, 0x76, 0x2c, 0xb8, 0xd8, 0x2e, 0x36,
    0xdb, 0x69, 0xb3, 0x14, 0x95, 0xbe, 0x62, 0xa1, 0x3b, 0x16, 0x66, 0xe9, 0x5c, 0x6c, 0x6d, 0xad,
    0x37, 0x61, 0x4b, 0xb9, 0xe3, 0xba, 0xf1, 0xa0, 0x85, 0x83, 0xda, 0x47, 0xc5, 0xb0, 0x33, 0xfa,
    0x96, 0x6f, 0x6e, 0xc2, 0xf6, 0x50, 0xff, 0x5d, 0xa9, 0x8e, 0x17, 0x1b, 0x97, 0x7d, 0xec, 0x58,
    0xf7, 0x1f, 0xfb, 0x7c, 0x09, 0x0d, 0x7a, 0x67, 0x45, 0x87, 0xdc, 0xe8, 0x4f, 0x1d, 0x4e, 0x04,
    0xeb, 0xf8, 0xf3, 0x3e, 0x3d, 0xbd, 0x8a, 0x88, 0xdd, 0xcd, 0x0b, 0x13, 0x98, 0x02, 0x93, 0x80,
    0x90, 0xd0, 0x24, 0x34, 0xcb, 0xed, 0xf4, 0xce, 0x99, 0x10, 0x44, 0x40, 0x92, 0x3a, 0x01, 0x26,
    0x12, 0x1a, 0x48, 0x68, 0xf5, 0x81, 0x8b, 0xc7, 0xd6, 0x20, 0x0a, 0x08, 0x00, 0x4c, 0xd7, 0x74,
};

Однако, все тайное рано, или поздно, становится явным, и способ выбора узла замены не исключение. Команде криптографов из Люксембурга, возглавляемой Алексом Бирюковым, удалось обнаружить определенного рода закономерности в статистических характеристиках узла замены, что, в свою очередь, позволило им восстановить способ его получения. Подробнее об этом способе можно почитать в их статье, опубликованной на iacr.org.

Секретная структура узла замены

Алгоритмическая оптимизация

Команде исследователей из ОАО «ИнфоТеКС», а конкретно Михаилу Бородину и Андрею Рыбкину, удалось позаимствовать алгоритмическую оптимизацию умножения вектора на столбец у скоростных реализаций шифра AES (Rijndael), которая позволяет заменить классическую реализацию умножения за O(n^2) умножений в поле на O(n) сложений по модулю два векторов длины O(n) с использованием предвычисленных таблиц, и о которой было доложено на конференции РусКрипто, если мне не изменяет память, в 2014 году.

Вкратце, оптимизация заключается в следующем: допустим, в результате произведения некоторого вектора U

$U = \left( u_0, u_1, \dots, u_{n - 1} \right) \in \left(\mathrm{GF}(256)\right)^n$

на матрицу A

$A = \begin{pmatrix} a_{0, 0} & a_{0, 1} & \cdots & a_{0, n-1} \a_{1, 0} & a_{1, 1} & \cdots & a_{1, n-1} \\vdots & \vdots & \ddots & \vdots \a_{n-1, 0} & a_{n-1, 1} & \cdots & a_{n-1, n-1} \end{pmatrix}_{n \times n} \in \left( GF(256) \right)^{n \times n}$

получился вектор V:

$V = U \times A = \left( v_0, v_1, \dots, v_{n-1} \right).$

Традиционный способ вычисления компонент этого вектора заключается в последовательном скалярном умножении строки вектора U на столбцы матрицы A:

$v_i = \bigoplus_{j = 0}^{n-1} u_j a_{j, i}$

Вычисление каждой из n компонент вектора V подразумевает n операций умножения в поле и n-1 операцию сложения по модулю 2, так трудоемкость вычисления всех компонент составляет O(n^2). Да, конечно, можно не умножать в поле каждый раз, можно заранее вычислить таблицы логарифма и экспоненты; можно даже заранее вычислить произведения всех возможных байт на элементы матрицы (матрица ведь фиксирована и не меняется в процессе шифрования), и хранить ~256 таблиц по 256 байт-произведений. В матрице есть одинаковые элементы? Отлично, число таблиц можно сократить, но асимптотическая сложность не изменится.

А можно пойти другим путем. Вместо того, чтобы вычислять каждую компоненту вектора-произведения как сумму n однобайтовых прозведений, воспользуемся особенностью умножения вектора на матрицу и будем вычислять сразу все компоненты вектора как сумму n векторов:

$V = \left( \bigoplus_j m_j a_{j, 0}, \bigoplus_j m_j a_{j, 1}, \dots, \bigoplus_j m_j a_{j, n-1} \right) = \bigoplus_j m_j \left( a_{j, 0}, a_{j, 1}, \dots, a_{j, n-1} \right).$

Казалось бы, что изменилось? Те же операции, но в другом порядке. Замечу, однако, что, во-первых, повысилась разрядность слагаемых с одного байта до n байт, и такие суммы можно (и нужно) вычислять в длинных регистрах, а, во-вторых, каждое слагаемое является покомпонентным произведением одного (!) байта вектора на фиксированную строку матрицу.

Вот здесь поподробнее: можно заранее вычислить произведения вида

$m_i \times \left( a_{i, 0}, a_{i, 1}, \dots, a_{i, n-1} \right) \quad \forall m_i \in \mathrm{GF}(256),$

то есть умножить известную строку i матрицы A на все возможные значения байта i вектора U, и вместо умножения очередного байта на эту строку просто считывать произведение из таблицы. Тогда умножение вектора на матрицу сводится к считыванию n строк-произведений из заранее вычисленной таблицы и побитовое сложение этих строк для получения результирующего вектора V. Вот так, достаточно просто, можно сильно упростить умножение вектора на матрицу до O(n), если сложение векторов считать элементарными операциями.

В случае ГОСТ Р 34.12 '15 n = 16, так, вектора имеют длины в 16 байт, или 128 бит, и очень здорово помещаются в длинные XMM регистры, а для их сложения предусмотрены дополнительные процессорные инструкции, например, pxor.

Все очень здорово, но как быть с узлом замены? Читатель наверняка заметит, что при наличии побайтовых узлов замены, которые в общем случае не векторизуются, все алгоритмические прелести такого вычисления L-преобразования нивелируются стоимостью загрузки векторов в регистры до преобразования и их выгрузки после преобразования. Хороший вопрос.

Хороший, и очень изящно решаемый. Оказывается, узлы замены можно просто «склеить» с L-преобразованием, заменив вычисляемые заранее строки произведения с

$m_i \times \left( a_{i, 0}, a_{i, 1}, \dots, a_{i, n-1} \right) \quad \forall m_i \in \mathrm{GF}(256),$

на

$\pi(m_i) \times \left( a_{i, 0}, a_{i, 1}, \dots, a_{i, n-1} \right) \quad \forall m_i \in \mathrm{GF}(256),$

Тогда один полный цикл шифрования сводится к

смешиванию с ключом (pxor),
применению склеенного преобразования LS (в наилучшем случае это 16 загрузок 128-битных векторов из кэша и 15 сложений pxor).

Конечно, такие оптимизации не бесплатны, для их использования потребуется, во-первых, вычислить и хранить в кэше единовременну одну из двух таблиц со строками-произведениями, каждая из которых содержит 256 * 16 * 16 байт, или 64 КБ. Почему таблиц две? Потому что обратное преобразование, используемое при расшифровании, потребует умножения на обратную к L матрицу, и повлечет за собой новые произведения.

Во-вторых, склеивание узлов замены с умножением на матрицу возможно только в том случае, если к блоку сначала применяют подстановку, а потом умножение, поэтому алгоритм расшифрования придется немного изменить. Открытый текст получается из шифртекста простым обращением всей схемы (все преобразования обратимы):

$P = X_0 S^{-1} L^{-1} \circ \dots \circ X_8 S^{-1} L^{-1} \circ X_9 (C).$

Заметим, что при расшифровании «в лоб» к промежуточному тексту сначала применяют умножение на обратную матрицу, а потом уже действие подстановкой, поэтому, чтобы склеить эти перобразования и тут, придется переупорядочить алгоритм расшифрования.

Замечу, что композиция преобразований

$V = L^{-1} X_{K_i} S^{-1} (U) = L^{-1} \left( S^{-1}(U) \oplus K_i \right)$

тождественна композиции

$V = L^{-1} S^{-1}(U) \oplus L^{-1} \left( K_i \right) = X_{L^{-1} (K_i)} L^{-1} S^{-1} (U)$

в силу линейности преобразования L. Тогда расшифрование можно осуществить следующим образом:

$P = X_{K_0} S^{-1} \circ \left( X_{L^{-1} (K_1)} L^{-1} S^{-1} \right) \circ \dots \circ \left( X_{L^{-1} (K_8)} L^{-1} S^{-1} \right) \circ X_{L^{-1} (K_9)} L^{-1} S^{-1} S (C)$

Здесь каждое из преобразований, обратных к SL, можно осуществлять по схеме, аналогичной к рассмотренной. Вычисленные таблицы строк-произведений постить не буду, — они слишком большие даже для спойлеров; их можно найти, например, здесь.

Оптимизация с использованием SSE2

В принципе, с базовыми преобразованиями все понятно, осталось все эти оптимизации положить на asm.
Для работы с блоками предлагаю использовать набор инструкций SSE2, будем использовать инструкции movdqu и movdqa для загрузки и выгрузки данных в регистры, инструкции pxor, pand, pandn для булевых операций, инструкции psrlw и psllw для побитовых сдвигов, pextrw для выгрузки байт регистра.

Да, есть еще одна тонкость реализации ГОСТ Р 34.12 '15. Кроме общеалгоритмических оптимизаций вроде описанных выше, для дальнейшего ускорения производительности нужно учитывать особенности ассемблера и особенности планировщика, который инструкции может поставить на параллельное исполнение на разных исполняющих устройствах.

Учет особенностей адресной арифметики

Первая особенность реализации алгоритма связана с тем, что, если не учитывать устройство предвычисленной таблицы и косвенной индексной адресации со смещением, то при компиляции можно получить примерно следующий выхлоп сложения с очередной строкой-произведением:

pextrb  xmmX,  eax, i                  ; выделение байта i (SSE 4.1) в 32--битный регистр eax
movzxd  rcx,   eax                     ; перемещение выделенного байта в 64--битный регистр rcx
add     rcx,   rcx                     ; удвоение значения байта
pxor    xmmY,  [rbx + 8*rcx + 0xi000]  ; вычисление смещения по таблице

В регистрах при этом хранятся:

rbx содержит адрес базового смещения таблицы,
xmmX содержит входной блок,
xmmY содержит выходной блок (аккумулятор, сумму),
eax и rcx используются для выделения и удвоения байта смещения.

Следует иметь в виду, что предвычисленная таблица устроена следующим образом:

uint8_t table[16][256][16],

то есть значения строк-произведений хранятся в этой таблице непрерывно, друг за другом, внешний индекс i соответствует i-ой строке матрице L-преобразования, средний индекс j равен i-ому байту входного блока, а внутренний индекс k соответствует индексу байта очередного слагаемого:

Xi = table[i][input[i]][0] ... [16]

Таким образом, адрес первого байта очередного слагаемого Xi выражается следующим образом:

[Xi] = rbx + (0x1000 * i) + (16 * input[i]),

где

(0x1000 * i) соответсвует смещению текущей строки (table[i]),
(16 * input[i]) соответсвует смещению текущего слагаемого Xi (table[i][input[i]]).

Так, значение текущего байта приходится умножать на 16, но адресная арифметика позволяет использовать максимальное значение коэффициента-множителя равное восьми. Поэтому компилятору приходится перекладывать значение байта в rcx, удваивать его, и только затем вычислять адрес Xi.

Для того, чтобы избежать подобных излишеств, можно воспользоваться идеологией SIMD, и вычислить приведенные смещения заранее, а не посредством адресной арифметики.

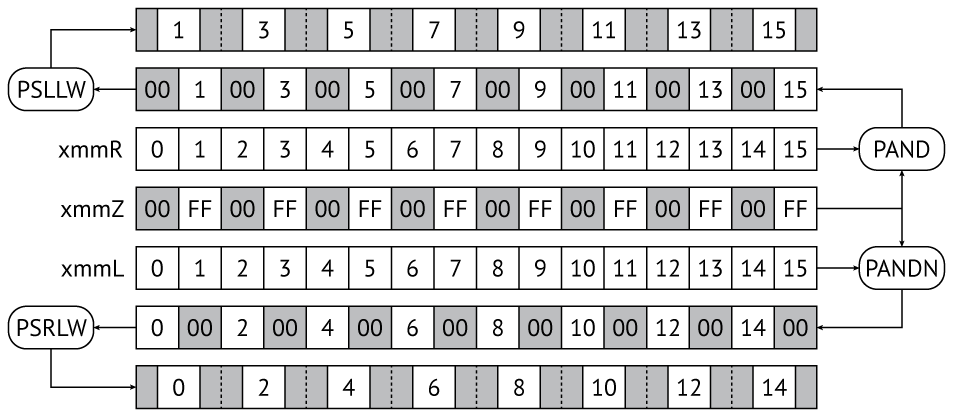
Предварительное вычисление приведенных смещений (слагаемые в адресе очередного Xi)

Здесь числами 0..15 обозначены соответствующие байты входного блока, а 00 и FF соответствуют нулевому байту и его инверсии.

С помощью маски 00FF 00FF 00FF 00FF 00FF 00FF 00FF 00FF и инструкций pand и pandn четные и нечетные байты входного блока выделяются в регистры левых и правых смещений соответственно; затем c помощью инструкций psrlw и psllw смещения приводятся (домножаются на 16) к значениям, пригодным для использования в адресной арифметике.
Так, каждое L-преобразование дополняется следующими строками:

pand    xmmR,  xmmZ                    ; выделение правых смещений
pandn   xmmL,  xmmZ                    ; выделение левых смещений
psllw   xmmR,  4                       ; приведение правых смещений
psrlw   xmmL,  4                       ; приведение левых смещений

и предварительной загрузкой маски в регистр xmmZ. Зато вычисление адресов слагаемых Xi теперь может быть осуществлено всего за две инструкции:

pextrw  eax,   i                       ; выделение приведенного смещения i
pxor    xmmY,  [rbx + rax + 0xi000]    ; вычисление смещения по таблице с помощью адресной арифметики

Учет специфики микроархитектуры

Большинство современных процессоров Intel и AMD имеют два, или более, исполняющих АЛУ, способных одновременно производить арифметические действия с различными регистрами, и планировщик, способный распределить блок выполняемых инструкций по различным АЛУ для параллельного выполнения с целью экономии процессорного времени.

Так, чередуя команды, использующие различные регистры, можно помочь процессору выполнять код параллельно. Склеенное LS-преобразование является двоичной суммой шестнадцати различных 128-битных чисел Xi, и, скорее всего, на современных процессорах может быть осуществлена в два параллельных потока (на одном ядре) с использованием двух аккумуляторов: левого и правого кэшей.

Пример кода, реализующего базовое преобразование (шифрование блока)

.code

extern    bitmask:xmmword
extern    precomputedLSTable:xmmword

encrypt_block  proc

initialising:
     movdqu         xmm0, [rcx]                        ; [unaligned] loading block
     lea            r8, [precomputedLSTable + 01000h]  ; [aligned] aliasing table base with offset
     lea            r11, [precomputedLSTable]          ; [aligned] aliasing table base
     movdqa         xmm4, [bitmask]                    ; [aligned] loading bitmask
     mov            r10d, 9                            ; number of rounds, base 0

round:
     pxor           xmm0, [rdx]                        ; [aligned] mixing with round key

     movaps         xmm1, xmm4                         ; securing bitmask from @xmm4
     movaps         xmm2, xmm4                         ; securing bitmask from @xmm4

     pand           xmm2, xmm0                         ; calculating offsets
     pandn          xmm1, xmm0
     psrlw          xmm2, 4
     psllw          xmm1, 4

     pextrw         eax, xmm1, 0h                      ; accumulating caches
     movdqa         xmm0, [r11 + rax + 00000h]
     pextrw         eax, xmm2, 0h
     movdqa         xmm3, [r8 + rax + 00000h]
     pextrw         eax, xmm1, 1h
     pxor           xmm0, [r11 + rax + 02000h]
     pextrw         eax, xmm2, 1h
     pxor           xmm3, [r8 + rax + 02000h]
     pextrw         eax, xmm1, 2h
     pxor           xmm0, [r11 + rax + 04000h]
     pextrw         eax, xmm2, 2h
     pxor           xmm3, [r8 + rax + 04000h]
     pextrw         eax, xmm1, 3h
     pxor           xmm0, [r11 + rax + 06000h]
     pextrw         eax, xmm2, 3h
     pxor           xmm3, [r8 + rax + 06000h]
     pextrw         eax, xmm1, 4h
     pxor           xmm0, [r11 + rax + 08000h]
     pextrw         eax, xmm2, 4h
     pxor           xmm3, [r8 + rax + 08000h]
     pextrw         eax, xmm1, 5h
     pxor           xmm0, [r11 + rax + 0a000h]
     pextrw         eax, xmm2, 5h
     pxor           xmm3, [r8 + rax + 0a000h]
     pextrw         eax, xmm1, 6h
     pxor           xmm0, [r11 + rax + 0c000h]
     pextrw         eax, xmm2, 6h
     pxor           xmm3, [r8 + rax + 0c000h]
     pextrw         eax, xmm1, 7h
     pxor           xmm0, [r11 + rax + 0e000h]
     pextrw         eax, xmm2, 7h
     pxor           xmm3, [r8 + rax + 0e000h]

     pxor           xmm0, xmm3                         ; mixing caches

     add            rdx, 10h                           ; advancing to next round key
     dec            r10                                ; decrementing round index
     jnz            round

last_round:
     pxor           xmm0, [rdx]                        ; [aligned] mixing with round key
     movdqu         [rcx], xmm0                        ; [unaligned] storing block

     ret

encrypt_block  endp

end

Заключение

Все описанные техники ускорения базового преобразования позволяют существенно повысить производительность шифра; в качестве конкретного примера могу привести числа, полученные на одном ядре Intel Core i7-2677M Sandy Bridge @ 1.80 GHz, это 120 МБ/с в версии с SSE инструкциями против 1.3 МБ/с в неоптимизированной версии.

Дальше — больше, ГОСТу можно придать дополнительное ускорение:

наличие регистров большей длины позволяет еще больше оптимизировать пакетное шифрование (только в режимах, которые допускают параллельную обработку блоков);
теоретически, замена вычисления подстановки по таблице значений вычислением с использованием секретной структуры узла замены, может дать небольшой прирост производительности при расшифровании.

Поиграть с различными реализациями базового преобразования ГОСТ Р 34.12 '15 можно, собрав у себя этот проект. Написан он на C99, на совершенство кода и абсолютную оптимальность он не претендует, но автор будет рад любой конструктивной критике. Для сборки потребуется CMake 3.2.1+ и компилятор, поддерживающий C99. Шифр реализован в трех версиях, по стандарту без существенных оптимизаций (compact), с предвычислениями, но без SIMD инструкций (optimised) и с использованием инструкций SSE2 (SIMD).

Непосредственные шаги сборки можно посмотреть в скрипте Travis CI в корне проекта, в комплект входят модульные тесты на контрольные примеры из стандарта (ключевое расписание, шифрование и расшифрование блока) на CTest и примитивный способ измерять производительность с использованием std::chrono на C++11.

Поделиться с друзьями

-->

Комментарии (41)

Dm3Ch
11.10.2016 22:07
#9853304
Заранее извиняюсь за, возможно, тупой вопрос. Я не специалист по криптографии. Но меня волнует вопрос — чем этот алгоритм лучше существующих мировых аналогов?
1. aaprelev
  11.10.2016 22:28
  #9853360
  +8
  Сложно что-то сказать о криптостойкости алгоритма по сравнению с зарубежными аналогами, шифр сравнительно новый и пока мало исследован. На мой взгляд, он во многом похож на AES, выглядит очень крепко, очевидных слабых мест в нем нет.
  
  В России более важными вопросами являются вопросы сертификации средств защиты информации; и с средствами, использующими зарубежную криптографию, вы попросту не пройдете сертификацию в органах. Поэтому здесь выбора особо и нет.
1. Gemorroj
  12.10.2016 00:03
  #9853534
  Если для работы, то эти алгоритмы по ГОСТУ нужны, например, для работы, образно говоря, с секретными документами (банковская сфера, финансовая, военка и т.д. и т.п.).
  Если для поиграться, то есть, например, такой подход: житель России используй AES (или другой зарубежный шифр), житель США — используй какой-нибудь ГОСТ.
  1. nckma
    12.10.2016 09:25
    #9854024
    +3
    А меня вот другое интересует.
    Разработка средств шифрования — в России это лицензируемый вид деятельности.
    Стоимость лицензий от 350 тыс. рублей.
    Но не знаю, что это значит. Если как вы говорите «поиграться» и я вставляю всем известный алгоритм (хоть ГОСТ, хоть AES/RC5/RC6) в свою программу — это я нарушаю какие-то законы или нет?
    Или не нарушаю никаких законов то того момента пока государство не купит мою программу? Или как?
    А если программа просто использует протокол https — это требует лицензии?
    Может конечно глупый вопрос…
    
    derwin
    12.10.2016 10:01
    #9854144
    100% не нарушаете, если у вас длина ключа менее 56бит.
    Ну а вообще — разработка и применение готового алгоритма это разные вещи.
    Если начнёте продавать программу/устройства — как минимум вам светит статья «незаконное предпринимательство».
    Ну и из опыта — любые операции с информацией, не представляющей гостайну, оказанные в рамках «для собственных нужд», допускаются к использованию на предприятии. Например я могу сам установить криптопро на предприятии, для этого не нужна лицензия ФСБ.
    немного почитать
    
    shifttstas
    12.10.2016 10:09
    #9854162
    +2
    А если программа просто использует протокол https — это требует лицензии?
    
    В любом случае, лучше занять очередь в пятницу, что бы по раньше освободится в субботу!
    
    keleg
    12.10.2016 11:58
    #9854520
    по оплате, насколько я понял из доклада Вартана Хачатурова (ссылка ниже) — оплачивать нужно только если сам занимаешься лицензируемым видом деятельности. ГОСТ можно хоть куда вставлять, это опенсорс в чистом виде.
    
    khim
    12.10.2016 19:50
    #9856002
    Или не нарушаю никаких законов то того момента пока государство не купит мою программу? Или как?
    Не знаю как сейчас, но 10 лет назад, когда я последний раз с этим сталкивался можно было использовать хоть чёрта лысого если не произносить запрещённых слов.
    
    В частности в системе, которую использовали на выборах (уж куда государственнее?) использовался GnuPGP с некоторыми изменениями в названиях сигнатур (без измнения алгоритмов, конечно). В документация вся эта хрень с ключами на 4096 бит и прочим проходила как «фирменный модуль повышения надёжности передачи данных и обнаружения несанцкионированных изменений» (или что-то в этом духе, точное название сейчас не скажу).
    
    Главное — не заявлять что вы что-то там шифруете и что-то там гарантируете. Как только вы это заявили — всё, требуются сертификаты и прочее. При работе с госструктурами иногда такие заявления нужны, иногда — нет.
    
    vanxant
    13.10.2016 13:30
    #9857374
    +1
    Лицензируется коммерческая разработка средств шифрования, здесь все слова важные.
    Если вы для себя пилите (и не только поиграться, но и реально использовать в рамках своей организации) — это не лицензируется.
    Если вы пилите продукт, но он опенсорс или вы просто (пока) его не продаёте в РФ — лицензия не нужна.
    Лицензируется именно разработка продукта (программ и возможно железок). Алгоритмы тут как бы сбоку, пока вы не выходите на продажи в госсектор — вы можете брать любые.
    Если ваш продукт нигде не называется «средством шифрования» и ничего такого не обещает — лицензия не нужна.
    Ну и наконец вопрос с получением лицензии не в деньгах, точнее не в сумме 350 тыс. Во-первых, там с документами тот ещё геморрой, вы на картриджи для ксерокса, нотариуса и затраты времени гендиректора, который будет по этим нотариусам с банками бегать два месяца, потратите не сильно меньше. А во-вторых, у вас в штате (именно в штате, всё в белую) должно быть как минимум 2 инженера с высшим (возможно, вторым высшим) конкретно по специальности ИБ, причём никакие смежные специальности не допускаются. Та же кафедра ИУ8 в Бауманке очень неплохо зарабатывает именно на получающих второе высшее по данной теме. И ваши расходы на их содержание в штате по-белому превысят те 350 тысяч за то время, пока оформляется лицензия.
1. vanxant
  12.10.2016 00:08
  #9853540
  +6
  Здесь сначала нужно определиться, что такое «лучше» для алгоритма шифрования, и относительно интересов кого это «лучше» отсчитывается.
  И вот для системных (=используемых на уровне государства и выше) шифров единственное разумное «лучше» — это пуленепробиваемая стойкость.
  Ну, представьте, что некто взломал шифр, которым банки подписывают сообщения о переводе денег. И теперь может лепить поддельные сообщения на тему «ооо ромашка переводит ооо вектор сто тыщь миллионов». Хотя у «ромашки», возможно, таких денег отродясь не было, сообщение подписано банком ромашки и будет исполнено. Представили? Это мгновенный крах банковской системы и моментальная остановка экономики страны, потому как другого способа перевода крупных сумм, кроме как через банки, сегодня нет.
  
  Потенциальные векторы угроз стойкости шифров можно разделить на три больших класса:
  
  1. Баги реализации в конкретной библиотеке. Ну, из недавно нашумевшего — история с хартблидом в либе OpenSSL. Поскольку либа популярная, пострадали очень многие. Такие ситуации неприятны, но лечатся относительно легко: патчем либы либо переходом на более другую библиотеку. Сам стандарт тут не при чём и его не трогают.
  
  2. Баги в алгоритме, которые делают возможным взлом шифра на обычном ПК или хотя бы на мощном суперкомпьютере. Пример: первые алгоритмы шифрования в сетях GSM. Лечится очень тяжело: нужно менять алгоритм, нужно внедрять новый алгоритм вообще везде, а это очень много времени и денег. Современные смартфоны, например, всё ещё несут на борту старые алгоритмы шифрования на случай, если где-то ещё встречаются старые базовые станции, и наоборот. Если удастся взломать одно или другое, можно вынудить вторую, невзломанную железку перейти на старый шифр, после чего перехват разговора становится делом техники.
  Для защиты от подобных атак, кстати, помогает тактика неуловимого Джо. При прочих равных лучше иметь свой алгоритм, просто потому что он не самый распространённый в мире, и его будут тупо реже пытаться взламывать.
  
  3. Сознательно внесённые в шифр бэкдоры. Есть обоснованное мнение, что все вот эти якобы случайные таблицы коэффициентов — нифига не случайны, и к ним есть «мастер ключ», резко снижающий стоимость вскрытия перебором. То есть хакер Вася или там Джон обламает зубы на ультрасложном матане и нехватке вычислительных мощностей, но вот заказчики бэкдора в погонах смогут при необходимости прочитать или подделать нужное сообщение. Точно не все подряд сообщения в потоке, но как минимум нужные им для конкретной злодейской задачи.
  Звучит как теория заговора, но здесь можно много всего вспомнить, от наездов федералов на pgp до откровений Сноудена и продуктов жизнедеятельности Яровой.
  И защита от таких бэкдоров на уровне государства может быть только одна — свои алгоритмы со своими православными бэкдорами.
  1. khim
    12.10.2016 19:56
    #9856016
    +2
    Звучит как теория заговора, но здесь можно много всего вспомнить, от наездов федералов на pgp до откровений Сноудена и продуктов жизнедеятельности Яровой.
    А не проще вспомнить реальную историю?
1. keleg
  12.10.2016 11:48
  #9854496
  +1
  Есть хорошее свежее видео " для непосвященных" про алгоритмы ГОСТ — доклад Вартана Хачатурова, OSSDEVCONF-2016. Автор — сборщик дебиана, криптоэнтузиаст и чиновник минкомсвязи :-)
  Там вопрос мировых аналогов, закладок и всяческих мифов разобран довольно подробно.
  https://vimeo.com/185219716
1. zapparello
  14.10.2016 13:15
  #9859958
  Надо спрашивать — чем он лучше предыдущего ГОСТа.
  
  В свете сведений, опубликованных Сноуденом (о том, как NSA пропихивает для использования заведомо слабые алгоритмы) вопрос про мировые аналоги лучше не задавать.
  
  Он лучше предыдущего ГОСТа (не говоря уж о DES) как минимум тем, что длина ключа намного длиннее, и «подслушать» этот ключ становится намного сложнее (по «колебаниям мирового эфира»). При сертификации аппаратных средств шифрования это один из самых сложных тестов.
  1. Ivan_83
    17.10.2016 23:42
    #9864676
    У обоих длина ключа 256 бит.
    Вот размеры блоков разные.
    Если под колебаниями подразумевается выходные данные то хз, а вот если речь про тайминг атаки и побочные излучения то оно целиком зависит от реализации, для таких простых алгоритмов.
    (Простых относительно ECDSA/ГОСТ2001/2012 — DJB на ECDSA не одно ведро говна вылил из того что там константного времени добиться не реально ибо слишком много ветвлений зависящих от значения ключа)
    
    Я поддерживаю идею о национальной крипте, но:
    — наш стрибог — коряво имплементированная хайфа, в результате вместо 512 бит получили 260 (единственный стандарт где автор потрудился и сделал достойную референсную реализацию)
    — наш гост2001/2012 — это ECDSA со своими параметрами и расчётами перенесёнными из проверки в подписывание (или наоборот, уже не помню)
    — гост89 — вроде не плох, но размер блока маловат, а про кузнечик пока говорить рано, но в целом большие таблицы — не очень хорошо
    
    Лучше чем ничего но до идеала тоже не близко.
    
    cat_at_CERN
    20.10.2016 01:12
    #9868668
    Сначала для «пешеходов» наверное будет полезно про кузнечик от юного, но уже внятного поколения криптографов, экспертов ТК26 — «ГОСТ Р 34.12–2015: чего ожидать от нового стандарта?» — http://www.itsec.ru/articles2/crypto/gost-r-chego-ozhidat-ot-novogo-standarta/
    
    Пару слов про качество СТРИБОГа. На семинаре в Bristol Univ однажды была дискуссия по TUAK,
    который исходно прописан под KECCAK (SHA-3). Было также краткое обсуждение об инкапсуляции 34.11-2012 в конструкции TUAK = {TOPc; f1; f1*; f2; f3; f4; f5; f5*}, на что Teng Wu (Waterloo) классно заметил, что и SHA-3 и GOST примерно одинаково неидеальны, ну типа mert (fr), но вполне пригодны:-)

omegicus
11.10.2016 23:51
#9853516
большое спасибо за статью! давно увлекаюсь шифрами.
1. Kolyuchkin
  12.10.2016 08:35
  #9853942
  -1
  Если Вы «давно увлекаетесь шифрами», то эта статья для Вас не должна была привнести ничего нового) Она полезна в первую очередь новичкам)

Decker
12.10.2016 01:11
#9853668
+1
Попробовал собрать проект под Visual Studio 12 2013 (MSVC 18.0.40629.0), собралось с двумя незначительными правками. В benchmark.cpp добавил:
```
#ifdef _MSC_VER
	#include <algorithm>
#endif
```
Без него компилятор ругался на std::generate_n… а в optimised.c добавил:
```
#ifdef _MSC_VER
	#define restrict __restrict
#endif
```
Может быть есть и более «красивое» решение для сборки под MSVC…
1. mayorovp
  12.10.2016 06:42
  #9853828
  Первое исправление надо добавлять независимо от компилятора, потому что функция std::generate_n и правда находится в <algorithm>
  1. aaprelev
    12.10.2016 07:25
    #9853878
    @Decker, mayorovp Спасибо, ошибку с <algorithm> исправил.

Ivan_83
12.10.2016 02:10
#9853722
«при этом «Магма» — всего лишь новое название для старого, всем хорошо известного блочного шифра ГОСТ 28147 '89» — в магме порядок байт в блоке 64 бита заменён на обратный. Все контрольные примеры от магмы в гост89 дают другой результат.
Великая загадка — зачем это было делать сейчас, когда оно уже везде внедрено/реализовано.

Забавный факт, но гост89 типа вне закона с 1 января этого года, но всякие госзакупки и пр продолжают его использовать.

Референс выглядит всё так же ужасно как и в версии 3 конца прошлого года :)

«теоретически, замена вычисления подстановки по таблице значений вычислением с использованием секретной структуры узла замены, может дать небольшой прирост производительности при расшифровании.»
ИМХО лучше не станет: таблицы и так сидят в кеше, а если сделать что то маленькое но с расчётами то получится дольше чем лазать в кеш л1/л2. Лучше не вымывать кеш, см ниже.

Скорость всё равно печальная.
У госта 89 чуточку лучше: http://www.securitylab.ru/analytics/480357.php
(если попробовать пересчитать то получится примерно 240 против 350 у гост89 по ссылке выше)

ИМХО AVX512 может улучшить ситуацию. По крайней мере у меня реализация стрибога на sse стабильно быстрее работала чем AVX, а потом я решил ещё тамошний 512 бит счётчик тоже сделать полностью на регистрах и оказалось что минимум тоже SSE2 который есть практически везде, правда пришлось некоторые фичи от более старших SSE «бэкпортировать», но скорость от этого не почти не пострадала.
Для варианта счётчика на регистрах уже стал требоваться AVX2, а поскольку он мало того что был только на одном компе но ещё и работал медленнее то я решил что смысла в нём нет.
В AVX512 помимо длинных регистров ещё вроде как их стало неприлично много, на кузнечика должно хватить.

Ещё лучше хотя бы опционально использовать _mm_stream_load_si128() из SSSE3 для загрузки блока данных, она не будет вымывать кеш, эффект особенно заметен если размер входных данных сильно больше кеша проца.
1. aaprelev
  12.10.2016 07:36
  #9853890
  Скорость всё равно печальная.
  У госта 89 чуточку лучше: http://www.securitylab.ru/analytics/480357.php
  Автор этой статьи, Андрей Луценко, обладает рядом патентов на скоростную реализацию ГОСТ 28147 '89, ему экономически выгодно пиарить прежний стандарт шифрования.
  
  Если же объективно говорить о производительности скоростных версий шифров на одной и той же платформе, то результаты оказались примерно следующие: ~170 МБ/с на поток для Магмы и ~150 МБ/с на поток для Кузнечика.
1. aaprelev
  12.10.2016 07:39
  #9853894
  Ещё лучше хотя бы опционально использовать _mm_stream_load_si128() из SSSE3 для загрузки блока данных
  За наводку на _mm_stream_load_si128 спасибо, попробую.
1. ru_crypt
  12.10.2016 07:57
  #9853902
  Рекорд скорости для Кузнечика сейчас — чуть более 330 МБ/с, но это проприетарные решения от вендоров и рассказывать, как это сделано, «они конечно не будут»(с). Так что автору просто мегареспектище за статью. Надеюсь будут еще.
  1. aaprelev
    12.10.2016 08:12
    #9853918
    @ru_crypt, уточните, 330 МБ/с в одном потоке? Какой процессор? Какой режим? Какой набор инструкций?
    
    Не могу представить себе способа еще почти втрое алгоритмически ускорить базовое преобразование. Думаю, что такие скорости достижимы при
    
    мощном процессоре с высокой тактовой частотой,
    
    наличии кэша первого уровня в 64 КБ (тогда в него вся таблица войдет),
    
    использовании более длинных регистров и конвейерном шифровании.
    
    ru_crypt
    12.10.2016 08:20
    #9853928
    Информация была представлена на CTCrypt, презентация выложена здесь: https://www.slideshare.net/secret/8AC2FSDNCZiyZv
    
    О скоростях слайды начинаются с 45-го (из 55).
    
    Подробности, полагаю, вполне можно запросить у авторов презентации.
    
    ru_crypt
    12.10.2016 08:30
    #9853934
    Режим гаммирования, в одном потоке. Core i5-6500, AVX.
    
    Частота 3.2 GHz, ничего необычного.
    64 KB в кэш первого уровня заведомо не войдет.
    А насчет длинных регистров и конвейеров — тут уж точно нужно к авторам презентации обратиться за комментариями…
    
    aaprelev
    12.10.2016 08:48
    #9853956
    +1
    Спасибо, надо будет пореверсить после релиза новой версии криптопровайдера.
1. ru_crypt
  12.10.2016 18:28
  #9855832
  «гост89 типа вне закона с 1 января этого года,»
  
  Отмечу, что ГОСТ 28147-89 никто не выводил (и пока не собирается) из действия, несмотря на ввод ГОСТ Р 34.12-2015.

shifttstas
12.10.2016 10:10
#9854172
+1
Как дела обстоят с закладками в шифре? надеялся увидеть этот пункт есть они или нет.
1. aaprelev
  12.10.2016 10:14
  #9854194
  +1
  @shifttstas Если они есть, мы об этом не узнаем ;)
1. AleksGRV
  12.10.2016 23:29
  #9856420
  https://eprint.iacr.org/2015/812.pdf
  1. aaprelev
    12.10.2016 23:35
    #9856426
    +1
    @AleksGRV Не осилили пост? В ней про структуру узлов замены написан целый раздел, даже ссылка на более полную работу представлена.
    
    Но даже известное устройство узлов замены не могу назвать закладкой шифра, ведь полученные таким способом узлы обладают действительно хорошими криптографическими свойствами, и очевидным образом использовать эту структуру для дешифрования шифртекста или определения цикловых ключей я не вижу.

ov7a
12.10.2016 15:36
#9855292
Со всеми оптимизациями скорости хотелось бы услышать что-нибудь про тайминг-атаки.
1. aaprelev
  12.10.2016 23:42
  #9856434
  Полагаю, что можно устроить атаки, аналогичные описанным здесь; время загрузки очередного слагаемого Xi на очередном цикле шифрования прямо зависит от значения соответствующего байта промежуточного текста.
  1. ov7a
    12.10.2016 23:47
    #9856444
    По ссылке, как я понял, авторы утверждают, что косяк в самом алгоритме AES, а не в какой-то его конкретной реализации. Мой вопрос относился именно к проблемам, которые всплывают из-за оптимизации/ускорения работы алгоритма.
    
    aaprelev
    12.10.2016 23:56
    #9856460
    +1
    Я вам ответил именно на ваш вопрос ;) ГОСТ во многом похож на AES; можно устроить очень похожие атаки на время загрузки векторов из таблиц, оно прямо зависит от значений байт промежуточного текста. Таблицы появляются только в оптимизированной версии шифра. В теории, при известном открытом тексте и точном способе измерять это время, можно попробовать определить байты первых двух цикловых ключей (половин секретного ключа). Но это тема отдельной статьи.

zapparello
14.10.2016 13:12
#9859936
Не очень понятно, зачем было оптимизировать полную схему преобразования на «полноформатном» процессоре, когда давно уже известна оптимизация (от какого-то горячего финского парня, исходники бродят по сети), позволяющая свести операцию к небольшому количеству операций исключающее-или с константами из относительно небольшого массива (64к для шифрования и 192к для дешифрования, если мне не изменяет память).

В таком варианте переложение алгоритма на SSE инструкции дают порядка >200Mb/s на каком-то core i5, на котором я пробовал. Да и то, думаю, скорость упирается в скорость обмена с памятью, сама скорость выполнения операции XOR на порядки выше.

Впрочем, это имеет определённый смысл как упражнение в программировании, а также как тренировку перед имплементацией алгоритма для более слабых процессоров, у которых 256к таблиц не влезает в кэш.
1. aaprelev
  17.10.2016 07:32
  #9862964
  Не утрудитесь ссылочкой на оптимизацию, о которой вы говорите? Ведь в посте полный цикл как раз сводится к небольшому количеству (15) операций исключающее ИЛИ (XOR) с константами из небольшого массива (64 КБ для шифрования и 64 КБ для расшифрования).
  1. zapparello
    20.10.2016 12:01
    #9869172
    Не дочитал Вашу статью до конца, уж извините. Дошёл до формул и подумал что дальше Вы по ними оптимизацию на SSE делаете :)
    
    Вот исходники, аж от 14го года
    https://github.com/mjosaarinen/kuznechik
    Насчёт 192к я соврал, это суммарный размер таблицы для шифрования и дешифрования.
    Таблицы дешифрования занимают 128к (две таблицы по 64к), таблицы шифрования занимают 64к.
    Шифрование несколько медленнее (но не в два раза, как можно было бы подумать :))
    Если при дешифровании Вы сумели обойтись всего одной таблицой в 64к, тогда Ваша статья заслуживает более глубокого изучения :)
  1. zapparello
    20.10.2016 12:06
    #9869186
    Кстати, подумалось, что «секретная» структура узла замены на самом деле просто реверс-инжиниринг формулы самопального генератора псевдослучайных последовательностей, которой воспользовались авторы алгоритма для генерации узла замены :)