Александр 4110 Шаенко (экс-инженер Даурия Аэроспейс, ныне главарь проекта краудсорсингового спутника «Маяк») и Степан Тезюничев пишут открытый софт для моделирования теплового режима спутников.

Репозиторий тут.



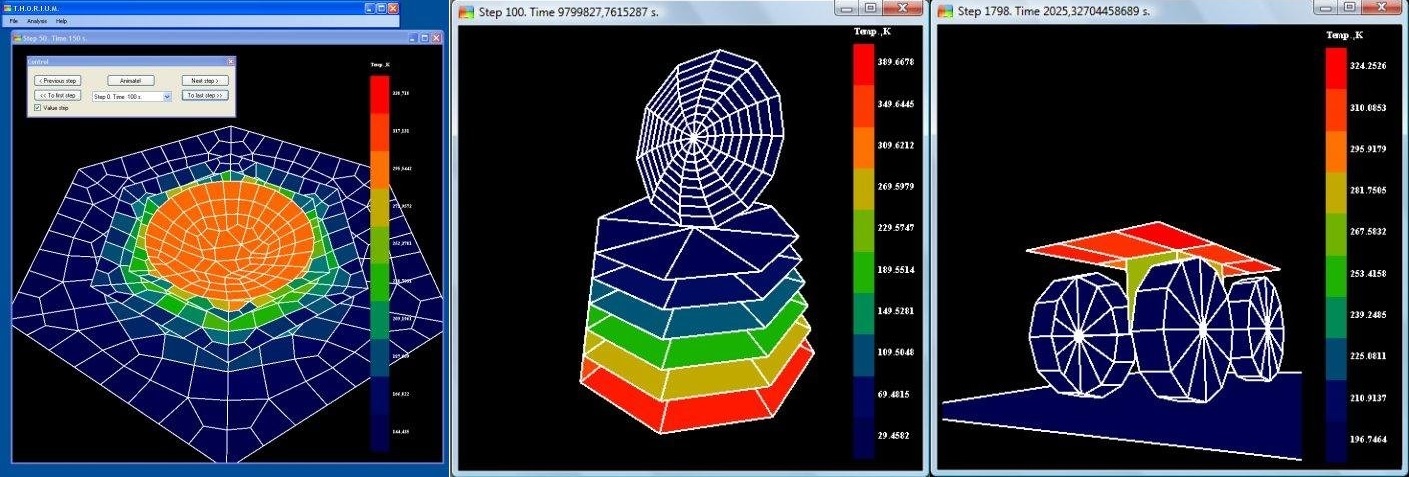
До этого, Саша писал дисер — «Метод решения задачи лучистого теплообмена без матрицы угловых коэффициентов» (диссертация, автореферат). Код тут. (он на VB.NET, тормозной, но работает и даже есть документация)

Космоинженеры используют метод Монте-Карло и до них вдруг дошло, судя по всему, система дифференциальных уравнений является стохастической, раз их часть получается методом случайных испытаний.

Парни хотят написать алгоритм, который решал бы систему дифуров как можно быстрее, и поэтому им нужна консультация математика-специалиста в области численного решения стохастических дифференциальных уравнений.

Основную сложность ребята вроде решили, построив массивно-параллельный алгоритм расчета хода излучения с методом Монте-Карло на CUDA. Теперь они хотят использовать для интегрирования своей системы, а она большой размерности, порядка 100 тыс. неизвестных, и жесткая, подходящий метод интегрирования по времени. Обычные явные методы требуют слишком мелкого шага по времени, а неявные требуют много раз вычислять правую часть, что ресурсозатратно.

Поэтому и нужно найти или построить такой метод интегрирования, который подходил бы для такого сочетания требований и позволял бы считать быстро.

Для чего это надо

Сейчас в России и в мире в целом нет открытого софта, который был бы заточен под расчет теплообмена спутников. Те коммерческие, которые есть, стоят десятки и сотни тысяч долларов и для обычных людей недоступны. Есть, конечно, открытые коды просто для расчета теплообмена, но чтобы на них полноценные посчитать сколько-нибудь реальный спутник, нужно изрядно поплясать.

Вы скажете, что для обычных людей они и не нужны, но это только до тех пор, пока вы не хотите сделать собственную маленькую компанию по созданию спутников. У большинства отечественных частных космических фирм нет денег на такой софт, да и у многих зарубежных нет тоже.

А если вы студент, который проектирует собственный спутник на курсовом или дипломном проекте? Триальной версии на 30 дней может и не хватить.

А если вам хочется разобраться в лучистом теплообмене? Или использовать хорошую реализацию метода трассировки хода лучей для других приложений?

Одним словом, приложений будет много и не только космических.

T.H.O.R.I.U.M.

Идея T.H.O.R.I.U.M. родилась у Шаенко в далеком 2007 году на конференции IASS в Венеции и развилась в размышлениях над автоматизацией расчетов прочности интерцепторов для пассажирского самолета 787 в московском отделении компании Boeing.


"Радиоастрон"

В то время Александр учился в аспирантуре Астрокосмического центра ФИАН им. Лебедева. Там, в то время заканчивали делать космический телескоп “Радиоастрон” и задумывались о “Миллиметроне”.


"Миллиметрон"

В «Миллиметроне» нужно было несколько лет поддерживать большое 10-метровое зеркало при температуре около 4 К (-269 С). Для этого зеркало планируется поместить в тень многослойного зонтика из полимерной металлизированной пленки, который бы защищал нежную аппаратуру от теплового излучения Солнца и Земли. Зонтик назвали “тепловой экран”. Точно такой же есть и у американского конкурента JWST, Космического телескопа Джеймса Вебба.

Реальная форма теплового экрана — это мятые двадцатиметровые полотнища пленки с небольшим расстоянием между ними. Это значит, что по-хорошему надо моделировать каждую более-менее большую складочку, чтобы понять как между ними будет распределяться тепло. К тому же разные слои имеют очень сильно различающуюся температуру — от примерно +100 С на освещенном Солнце слое до -223 С на слое, обращенном к зеркалу. При таком разбросе свойства материалов менялись очень сильно.

Существующие расчетные коды не позволяли все это учесть и поэтому на свет появился T.H.O.R.I.U.M. — Thermooptic radiation iterative universal module. В его основе лежат две идеи, возникшие в конце 2007 года:

1. Для расчета хода излучения в трехмерной графике разработано множество программных и аппаратных средств и так как в космосе внешний теплообмен — лучистый, то можно воспользоваться наработками из графики в расчете теплообмена.
   
   
2. Если хочется посчитать сложные конструкции с большим количеством элементов в модели, то не стоит запоминать перед началом расчета какие элементы с какими обмениваются излучением. Выгоднее смотреть это на каждом шаге интегрирования по времени.

Эти два принципа были реализованы и старом коде на VB.NET и с новом. “Миллиметрон” был спасен, а T.H.O.R.I.U.M. зажил своей собственной жизнью, помогая проектировать системы обеспечения теплового режима (СОТР) для малых аппаратов. Например, СОТР DX1 и МКА-Н, малых аппаратов Даурии были спроектированы с его помощью.

Видос старого T.H.O.R.I.U.M. с Дауриевским МКА-Н




DX1 в T.H.O.R.I.U.M.

С точки зрения математики, T.H.O.R.I.U.M. решает систему дифференциальных уравнений нестационарного радиационно-кондуктивного теплообмена с учетом переменности теплофизических и термооптических характеристик материалов. Уравнения эти выглядят вот так:



где
c_i — удельная теплоемкость i-го элемента; ?_i — его плотность; V_i — объем элемента; T_i — температура элемента; t — время; Nⁱ_n — количество элементов, имеющих общую грань с i-м элементом; Qn_kⁱ — мощность, передаваемая от k-го соседа i-го элемента посредством теплопроводности; S_i — площадь i-го элемента; Qe_i — плотность исходящего лучистого потока i-го элемента; Qr_ij — мощность, передаваемая от j-го элемента на i-й элемент посредством излучения; N — количество элементов в модели; Qr_j^m — мощность излучения, испускаемого m-ым внешним источником и поглощенного в i-ом элементе; M — количество источников излучения; Qi_i^p — тепловыделение от p-го внутреннего источника тепла в i-ом элементе, P — количество внутренних источников тепла.

Число N может быть больше 10⁵, свойства элементов и граничные условия могут очень резко меняться от времени, например, при включении какого-то прибора или выходе на Солнце из тени, интегрировать нужно 10-20 витков, а это порядка 120000 секунд.

Так что поиск хорошего метода интегрирования такой системы был бы очень полезен и авторам, и космонавтике, и инженерному делу в целом.

Кто заинтересовался — пишите в комменты или на почту Александру — ark4110@gmail.com.