Этим постом мы завершаем серию лекций с Data Fest. Одним из центральных событий конференции стал доклад Дмитрия Ветрова — профессора факультета компьютерных наук НИУ ВШЭ. Дмитрий входит в число самых известных в России специалистов по машинному обучению и, начиная с прошлого года, работает в Яндексе ведущим исследователем. В докладе он рассказывает об основах байесовского подхода и объясняет, какие преимущества дает этот подход при использовании нейронных сетей.
Под катом — расшифровка и часть слайдов.
Времени немного, буду скакать по верхушкам. Интересующиеся могут смотреть слайды — там более строгий вывод и много красивых и разных формул. Будем надеяться, что будет не очень скучно.
О чем я буду говорить. Попытаюсь дать краткую характеристику байесовских методов, байесовского подхода как теории вероятности, как задачи машинного обучения. Этот подход был достаточно популярен в 90-е и нулевые годы — до того, как началась глубокая революция, вызванная триумфальным шествием глубинных нейронных сетей. Какое-то время казалось: зачем все эти байесовские методы нужны, у нас нейросети и так прекрасно работают. Но как часто бывает, в какой-то момент выяснилось, что можно объединить преимущества нейросетевого и байесовского подходов. В первую очередь — благодаря тому, что появились техники вариационного байесовского вывода, и эти модели не противоречат друг другу, а наоборот, прекрасно дополняют, взаимно усиливая друг друга.
В каком-то смысле я воспринимаю это как направление дальнейшего развития современного машинного обучения и глубинного обучения. Важно понимать, что нейронные сети не являются панацеей. Они — всего лишь важный шаг в правильном направлении, но далеко не последний шаг. Я попытаюсь поговорить о следующем возможном шаге в теории машинного обучения. А следующий докладчик, Сергей Бартунов, попытается заняться деконструкцией мифа и в каком-то смысле продолжить мысль, что глубинное обучение — не панацея. Но Сергей подойдет к этому несколько с другой стороны, предоставит некий более глобальный взгляд.

Итак, что же такое байесовский подход? Весь подход базируется на одной единственной формуле или теореме. Теорема Байеса приведена в математической и концептуальной формах.
Ключевая идея. Предположим, есть какая-то неизвестная величина, которую мы бы хотели оценить по каким-то ее косвенным проявлениям. В данном случае неизвестная величина — ?, а ее косвенное проявление — у. Тогда можно воспользоваться теоремой Байеса, которая позволяет наше исходное незнание или знание о неизвестной величине, априорное знание, трансформировать в апостериорное после наблюдения некоторых косвенных характеристик, как-то косвенно характеризующих неизвестную величину ?.
Ключевая особенность формулы — в том, что на вход мы подаем априорное распределение, кодирующее наше незнание или нашу неопределенность о неизвестной величине, и что выходом также является распределение. Это крайне важный момент. Не точечная оценка, а некая сущность того же формата, что был на входе. Благодаря этому становится возможным, например, использовать результат байесовского вывода, апостериорное распределение, как априорное в какой-то новой вероятностной модели и, таким образом, охарактеризовать новую неизвестную величину с разных сторон путем анализа ее различных косвенных проявлений. Это первое достоинство, благодаря которому удается получить свойство расширяемости — или композицируемости — разных вероятностных моделей, когда мы можем из простых моделей строить более сложные.
Второе интересное свойство. Простейшее правило суммирования произведения вероятностей означает: если у нас есть вероятностная модель — а другими словами, совместное вероятностное распределение на все переменные, возникающие в нашей задаче, — то мы, как минимум в теории, всегда можем построить любой вероятностный прогноз, спрогнозировать интересующую нас переменную U, зная какие-то наблюдаемые переменные О. При этом есть переменная L, которую мы не знаем и она нас не интересует. По этой формуле они отлично исключаются из рассмотрения.
Для любых сочетаний этих трех групп переменных мы всегда можем построить такое условное распределение, которое и укажет, как изменились наши представления об интересующих нас величинах U, если мы пронаблюдали величины О, предположительно связанные с U.

По сути, повсеместное применение формул Байеса дало рождение второму альтернативному подходу к теории вероятностей. Есть классический подход — на Западе нередко называемый частотным, фриквентистским, — и есть альтернативный байесовский подход. Вот краткая таблица, которую я привожу на всех своих лекциях и которая показывает различия между подходами. Естественно, они друг другу не противоречат. Они скорее друг друга дополняют. По этой табличке можно проследить, что у них общего и в чем различия.
Ключевое различие в том, что понимать под случайной величиной. В частотных терминах мы под случайной величиной понимаем величину, значение которой мы спрогнозировать не можем, не оценив какие-то статистические закономерности. Нужно что-то обладающее объективной неопределенностью, в то время как при байесовском подходе случайная величина интерпретируется просто в качестве детерминированного процесса. Он может быть полностью спрогнозирован. Просто в данном детерминированном процессе мы не знаем часть факторов, влияющих на исход. Поскольку мы их не знаем, мы не можем спрогнозировать исход детерминированного процесса. Значит, для нас данный исход выглядит как случайная величина.
Простейший пример — подбрасывание монетки. Речь идет о классической случайной величине, но мы понимаем, что монетка подчиняется законам классической механики и, вообще-то, зная все начальные условия — силу, ускорение, коэффициент сопротивления среды и т. д., — мы могли бы точно сказать, как монетка упадет: орлом или решкой.
Если вдуматься, подавляющее большинство величин, которые мы привыкли считать случайными, на самом деле случайны именно в байесовском смысле. Это какие-то детерминированные процессы, просто мы не знаем часть факторов этих процессов.
Поскольку один может не знать одни факторы, а другой — другие, возникает понятие субъективной неопределенности или субъективного незнания.
Остальное — прямые различия этой интерпретации. Все величины в байесовском подходе можно трактовать как случайные. Аппарат теории вероятностей применяется к параметрам распределения случайной величины. Другими словами, то, что в классическом подходе бессмысленно, в байесовском подходе обретает смысл. Метод статистического метода, вместо метода максимального правдоподобия — теорема Байеса. Оценки получаем не точечные, а вида апостериорного распределения, позволяющего нам комбинировать разные вероятностные модели. И в отличие от частотного подхода — теоретически обоснованного при больших n, а некоторые доказывают, например, при n, стремящихся к бесконечности, — Байесовский подход верен при любых объемах выборки, даже если n = 0. Просто в данном случае апостериорное распределение совпадет с априорным.

Простая иллюстрация. Известная притча о слепых мудрецах и слоне, показывающая, как модель можно зацепить.
Давайте представим: дано несколько слепых мудрецов и один слон. Задача — оценить массу этого слона. Мудрецы знают, что сейчас будут щупать некое животное. Какое именно — не знают, но они должны оценить массу.

Они все начинают с того, что кодируют свои представления о возможной массе животного в виде априорного распределения, поскольку теперь плотность распределения может определять простую меру нашего незнания о чем-то. Для кодирования указанных знаний мы можем просто использовать аппарат теории вероятностей.
Поскольку речь идет о мудрецах, они знают характерные массы животных на планете Земля. Поэтому они и получают примерно такое априорное распределение.
Первый мудрец подходит, щупает хвост и делает вывод, что, видимо, перед ним нечто змееобразное либо хвост крупного животного. Значит, в процессе своего байесовского вывода, объединив результаты своих представлений, которые можно выразить в виде вероятностной подели p1, он получает апостериорное распределение р(?) при условии х=1.
Дальше подходит другой мудрец, который может не щупать, а скажем, нюхать. Тут абсолютно другая модель. X2 — это величина совершенно из другого домена, косвенно характеризующая массу животного. В процессе своего байесовского вывода он использует в качестве априорного распределения не исходное, с которого все начинали, а результат вывода предыдущего мудреца. Тем самым мы можем объединить два совершенно различных измерения, два источника информации, в одной элегантной вероятностной модели.
И вот, проделав серию измерений, мы в конечном итоге получаем уже достаточно острое апостериорное распределение, почти точную оценку. Мы уже с высокой точностью можем сказать, какая масса была у животного. Это иллюстрация к третьему свойству — к extendibility, то есть к возможности модели всё время расширять и зацеплять.
Другое достоинство байесовского подхода, уже применительно к машинному обучению, — регуляризация. Благодаря учету априорных предпочтений мы препятствуем излишней настройке наших параметров в ходе процедуры машинного обучения и тем самым способны справляться с эффектом переобучения. Какое-то время назад, когда алгоритмы начали обучать на огромных объемах данных, считалось, что проблема переобучения снята с повестки дня. Но дело было исключительно в том, что люди психологически боялись переходить к нейросетям гигантского размера. Все начинали с небольших нейросетей, и они, при гигантских обучающих выборках, действительно не переобучались. Но по мере того, как психологический страх исчезал, люди начинали использовать сети всё большего размера.
Стали очевидными две вещи. Для начала — чем больше сеть, тем она в принципе лучше. Большие сети работают лучше, чем маленькие. Но большие сети начинают переобучаться. Если у нас количество параметров — 100 млн, то 1 млрд объектов — не очень большая обучающая выборка, и нам необходимо регуляризовывать процедуру такого машинного обучения.
Байесовский подход как раз дает прекрасную возможность делать это за счет введения априорного распределения на те параметры, на те веса нейронной сети, которые настраиваются в ходе процедуры обучения.
В частности, оказалось, что такая популярная техника эвристической регуляризации, как drop out, является частным случаем, грубым приближением для байесовской регуляризации. На самом деле речь идет о попытке сделать байесовский вывод.
Наконец, третье преимущество — возможность построения модели с латентными переменными. О ней подробнее.

У нас есть мотивирующий пример — метод главных компонент. Метод очень простой — линейное уменьшение размерности. Берем выборку в пространстве с высокой размерностью, строим ковариационную матрицу, проецируем на главную ось с соответствующим самым большим значением. Вот что геометрически здесь показано. И уменьшили размерность пространства с 2 до 1, сохранив максимум дисперсии, содержавшейся в выборке.
Метод простой, допускает решение в явном виде. Но можно альтернативно сформулировать иначе, в терминах вероятностной модели.

Представим, что наши данные устроены так: для каждого объекта есть его скрытое представление в пространстве маленькой размерности. Здесь оно обозначено как z. А мы наблюдаем линейную функцию от этого скрытого представления в пространстве с более высокой размерностью. Мы взяли линейную функцию и дополнительно добавили нормальный шум. Тем самым мы получили х, высокоразмерные данные, по которым нам крайне желательно восстановить их низкоразмерное представление.

Математически это выглядит так. Мы задали вероятностную модель, которая является совместным вероятностным распределением на наблюдаемые и скрытые компоненты, на x и z. Модель достаточно простая, выборка характеризуется произведением по объектам. Наблюдаемая компонента каждого объекта определяется скрытой компонентой, речь идет об априорном распределении на скрытой компоненте. И то и другое является нормальным распределением. Мы предполагаем, что в малоразмерном пространстве данные распределены априорно нормально, и наблюдаем линейную функцию этих данных, которая зашумлена нормальным шумом.
Нам задана выборка, представляющая собой высокоразмерное представление. Мы знаем x, мы не знаем z, и наша задача — найти параметр ?. ? — это матрица V, ?? и всё.
Указанную задачу можно сформулировать на байесовском языке как задачу обучения с латентными переменными. Чтобы применить обычный метод максимального правдоподобия, не хватает знания увеличения z. Оказывается, для этой техники существует стандартный подход, основанный на ЕМ-алгоритме и различных модификациях. Можно запустить итерационный процесс. На ЕМ-шаге приведены формулы, описывающие, что мы делаем. Можно теоретически показать, что процесс монотонный и гарантированно сходится к локальному экстремуму, но все-таки.
Возникает вопрос: а зачем нам применять итерационный процесс, когда мы знаем, что задача решается в явном виде?
Ответ простой. Для начала — алгоритмическая сложность. Сложность аналитического решения — O(nD?), в то время как сложность одной итерации ЕМ-алгоритма — O(nDd).
Если мы мысленно представим, что проецируем пространство размерностью 1 млн в пространство размерностью 10, и ЕМ-алгоритм сходится итераций за сто, то наша итерационная схема будет работать в 1000 раз быстрее, чем решение в явном виде.
Кроме того, важное достоинство: теперь мы нашу базовую модель, метод главных компонент, можем различными способами расширять в зависимости от специфики конкретной задачи. Например, мы можем ввести понятие смеси методов главных компонент, и сказать, что наши данные живут не в одном пространстве, линейном подпространстве меньшей размерности, а в нескольких. И мы не знаем, из какого подпространства пришел каждый конкретный объект.
Возникает смесь методов главных компонент. Формально модель записывается так. Просто ввели дополнительную номенклатуру скрытых дискретных переменных t. И опять же, ЕМ-алгоритм позволяет нам найти решение задачи почти по тем же формулам, хотя исходный метод главных компонент нам не позволял производить никакие модификации.

Еще одно — возможность работать в ситуациях, когда, допустим, для нашей выборки часть компонент х неизвестны, данные пропущены. Бывает такое? Сплошь и рядом. Несколько более экзотическая ситуация — когда нам известны скрытые представления части объектов, низкоразмерное представление, целиком или частично. Но опять же, такая ситуация возможна.
исходная модель метода главных компонент не способна учесть ни того, ни другого, в то время как вероятностная модель, сформулированная на байесовском языке, и то, и другое учитывает элементарно — простой модификацией ЕМ-алгоритма. Мы просто немного меняем номенклатуру наблюдаемых скрытых переменных.
Тем самым мы можем решать задачи обработки данных, когда какие-то произвольные фрагменты этих данных могут отсутствовать, не то что в стандартном машинном обучении, когда выделяется номенклатура наблюдаемых и как бы скрытых, целевых переменных и перемешиваться они никак не могут. Здесь возникает дополнительная гибкость.

Наконец, до недавнего времени считалось, что существенное ограничение байесовских методов состоит в том, что они, обладая высокой вычислительной сложностью, применимы к небольшим выборкам данных и не переносятся на большие данные. Результаты последних нескольких лет показывают, что это не так. Человечество наконец-то научилось обеспечивать масштабируемость байесовских методов. И люди тут же начали скрещивать байесовские методы с глубинными нейронными сетями.
О том, как масштабировать байесовский метод, я скажу пару слов, благо время еще есть.

Теорема Байеса. Хотим по известным X, M сказать что-то про Z, который как-то связан с X. Мы применяем теорему Байеса. Вопрос: какое здесь самое уязвимое место, какой самый тяжелый фргамент? Интеграл.
В тех редких случаях, когда интеграл берется аналитически, все хорошо. Другое дело, если он аналитически не берется — а ведь мы представляем, что говорим о высокоразмерных данных, и тут интеграл в пространстве размерностью не 1 или 2, а десятки и сотни тысяч.
С другой стороны, давайте запишем цепочку. Стартуем: ? p(X|Z) p(Z) dZ. Поскольку log P(X) dZ не зависит, это просто интеграл по всему Z, равный 1.
Второе действие. Выразили p(X), по этой формуле перенесли влево, p(Z|X) в знаменатель, записали под интегралом.
Теперь у нас числитель и знаменатель зависят от Z, хотя их частное дает p(X), то есть не зависит от Z. Тождество.
Дальше умножили то, что стоит под log, умножили на 1 и поделили на q(Z).
И последнее — разбили интеграл на две части. Тут видим: вторая часть — хорошо известная в теории вероятностей дивергенция Кульбака-Лейблера, величина неотрицательная и равная нулю тогда и только тогда, когда эти два распределения совпадают между собой. В каком-то смысле это аналог расстояния между распределениями. А напоминаю, наша задача оценить p(Z|X) хотя бы приближенно, выполнить байесовский вывод.
Эту величину мы посчитать не можем, здесь фигурирует p(Z|X). Зато отлично можем посчитать первое слагаемое. Каждое из слагаемых зависит от q(Z), но их сумма от q(Z) не зависит, потому что она равна log p(X). Возникает идея: а давайте мы будем первое слагаемое максимизировать по q(Z), по распределению.
Это означает, что, максимизируя первое слагаемое, мы минимизируем второе — которое показывает степень приближения q(Z) к истинному апостериорному распределению. И вот, тем самым, ключевая идея: мы свели задачу байесовского вывода, включающую в себя интегрирование в пространстве высокой размерности, к задаче оптимизации.
Задачу оптимизации человечество умеет решать хорошо даже при гигантских объемах данных.

Такой подход называется вариационный Байес. Ключевая идея — что вывод становится оптимизацией.
Какие у нас есть универсальные анализаторы, аппроксиматоры? Особенно пригодные для работы с большими данными? Нейронные сети.
Про стохастическую оптимизацию не успеваю сказать.

Здесь я уже сделал следующий шаг — обучение по неполной разметке. Дано Xtr, Z мы не знаем, и нам бы оптимизировать этот функционал по ?. Мы даже не можем его в явном виде посчитать, но зато, когда мы заменили его на вариационную нижнюю оценку L, появилась еще и зависимость от ? — поскольку мы хотим дополнительно левую часть оптимизировать по ?. Мы можем оптимизировать L одновременно по Q(Z) и по ?. Оптимизация по ? позволяет нам всё лучше описывать обучающую выборку, а оптимизация по Q(Z) позволяет всё точнее проводить байесовский вывод над скрытыми переменными Z.
Среди прочего оказывается, что такая модель допускает эффективную оптимизацию с помощью методов стохастической оптимизации. Они позволяют оптимизировать функцию, которую мы, может, даже не сможем посчитать ни в одной точке. Нам достаточно уметь считать для нее стохастический градиент и, быть может, какие-то дополнительные характеристики для дальнейшего ускорения сходимости.
Здесь оказывается, что никаких проблем нет. Стохастический градиент для вариационной нижней оценки может быть выражен по такой формуле, где мы сгенерировали Z из текущего Q(Z). Ну и всё, дальше можно дифференцировать. Тут есть некоторые тонкости, но о них я рассказать уже не успею.
По поводу того, как уменьшать дисперсию стохастического градиента. Нейробайесовский подход родился в тот момент, когда мы поняли, как эту дисперсию можно уменьшить, — потому что затем стало возможным применять байесовские техники в глубинном обучении и, как следствие, успешно решать новый спектр задач.
Расскажу об одной из них. Речь идет о вариационном автокодировщике — он представляет собой сравнительно прямолинейное обобщение методов главных компонент в его байесовской интерпретации. Вспоминаем: наверху формула для методов главных компонент. Есть скрытые переменные, априорно имеющие нормальное распределение в пространстве маленькой размерности, и есть наблюдаемые компоненты, которые просто являются линейной функцией от скрытых компонент. Плюс нормальный шум.
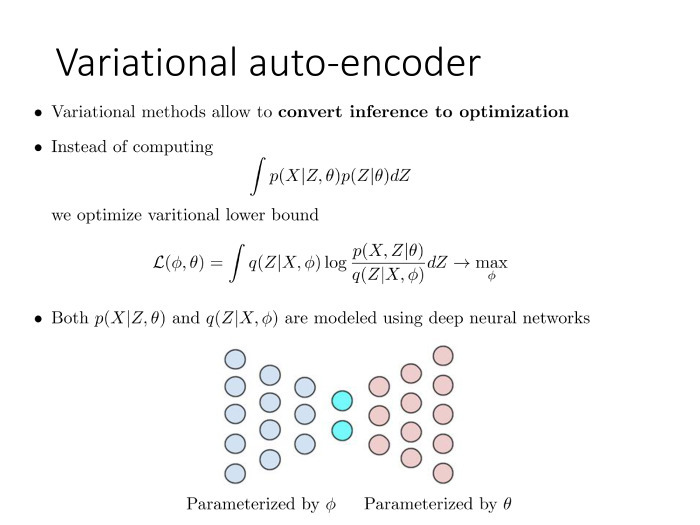
Казалось бы, давайте сделаем всё то же самое, только пусть будет не линейная функция, а что-нибудь более хитрое. Здесь так и сделано, ? и ? — теперь не линейные функции от латентного представления данного объекта. Пусть это будет выходом нейронной сети. Есть нейронная сеть, которая на вход получает Zi и выдает значение ? и ?, которое показывает распределение соответствующего Xi. Данная нейронная сеть имеет веса ?. В остальном модель та же самая. Единственное, мы вместо линейной функции поставили сюда нелинейную, определяемую нейронной сетью.

Всё бы хорошо, но проблема в следующем: в этой задаче строгий байесовский вывод, в отличие от метода главных компонент, уже сделать нельзя. Поэтому здесь приходится использовать ту вариационную технику, о которой я рассказал раньше. Мы переходим к вариационной оценке L, вводим распределение Q(Z), которое параметризуется через ?, и пусть это будет другая нейронная сеть. Чем богаче семейство распределений, где мы проводим оптимизацию, тем лучше. Самое богатое, что мы умеем оптимизировать на сегодняшний день, — нейронные сети, обладающие достаточной гибкостью.
Добавим вспомогательную нейронную сеть. У нее будут свои параметры ?. Сеть, которая принимает Z, возвращает X. Эта сеть — наоборот, принимает X и возвращает распределение на Z.
Такая техника очень похожа на то, что в нейронных сетях известно как модель автокодировщика. Только здесь все сформулировано на вероятностном языке, поэтому ее назвали вариационным автокодировщиком.

Для начала оказалось, что такая модель может быть обучена крайне эффективно. Значит, ее можно обучать на гигантских выборках данных. Чем больше выборки, тем выше качество аппроксимации и тем лучше мы решаем задачу уменьшения размерности, поиска низкоразмерных латентных представлений, выучивания представлений. В глубинном обучении их называют representations.
Одновременно мы оптимизируем нижнюю оценку на этот log и, по сути, восстанавливаем плотность в пространстве иксов. Как правило, пространство иксов является высокоразмерным — скажем, пространством изображений, видеозаписей, анкет пользователей социальной сети, некоторых объектов со сложной природой — и восстановить плотность в нем довольно проблематично. Но — возможно с помощью техники вариационного автокодировщика. Она была предложена приблизительно полтора-два года назад и казалась настолько успешной, что с тех пор появилось огромное количество модификаций, позволяющих учитывать априорные представления о структурах пространства, о латентных переменных, комбинировать эту технику с графическими моделями и т. д. Указанная область сейчас развивается взрывными темпами, и перед нами один из примеров того, как байесовские методы и, по сути, байесовский вывод были применены к задаче глубинного обучения. В данном случае глубинное обучение используется для уменьшения размерности пространства.
Это один из примеров, но далеко не единственный. Другой пример из известных мне — байесовское обоснование процедуры drop out. Исходно она была придумана инженерами для инженеров, и никто не мог членораздельно объяснить, почему она работает. Теперь мы знаем, почему. Мы знаем, что там задействован байесовский регуляризатор специального вида. Никто не мешает нам использовать другой регуляризатор и получить немного другую процедуру. Теперь мы можем не использовать drop out как черный ящик, как некую фиксированную процедуру, а модифицировать его в разные стороны, понимая, что лежало в основе этой процедуры.
Кроме того, в прошлом году была предложена техника карт внимания, attention maps, которая тоже позволила существенно расширить класс задач, решаемых нейронными сетями. Для начала речь идет о задачах генерации текста по изображению. В основе такой техники лежит вариационный байесовский вывод некоторого специального вида, но по сути — тоже базирующийся на оптимизации некоторой эволюционной оценки L(Q|?).
На этом закончу. Резюмируя, выскажу две ключевые мысли. Байесовский подход прекрасно комбинируется, и на наших глазах происходит все больше работ в этом направлении. Скажем, на главной конференции по машинному обучению NIPS аж четыре воркшопа, посвященных байесовским методам, и часть воркшопов — как раз по их скрещиванию с нейронными сетями.
Надеюсь, мне удалось донести преимущества байесовского подхода и сущность вариационного байесовского вывода, рассказать, благодаря чему байесовские методы удалось масштабировать и перенести на большие данные. А как мы дальше будем скрещивать и получать нейробайеса — увидим в ближайшие годы. Спасибо.
Под катом — расшифровка и часть слайдов.
Времени немного, буду скакать по верхушкам. Интересующиеся могут смотреть слайды — там более строгий вывод и много красивых и разных формул. Будем надеяться, что будет не очень скучно.
О чем я буду говорить. Попытаюсь дать краткую характеристику байесовских методов, байесовского подхода как теории вероятности, как задачи машинного обучения. Этот подход был достаточно популярен в 90-е и нулевые годы — до того, как началась глубокая революция, вызванная триумфальным шествием глубинных нейронных сетей. Какое-то время казалось: зачем все эти байесовские методы нужны, у нас нейросети и так прекрасно работают. Но как часто бывает, в какой-то момент выяснилось, что можно объединить преимущества нейросетевого и байесовского подходов. В первую очередь — благодаря тому, что появились техники вариационного байесовского вывода, и эти модели не противоречат друг другу, а наоборот, прекрасно дополняют, взаимно усиливая друг друга.
В каком-то смысле я воспринимаю это как направление дальнейшего развития современного машинного обучения и глубинного обучения. Важно понимать, что нейронные сети не являются панацеей. Они — всего лишь важный шаг в правильном направлении, но далеко не последний шаг. Я попытаюсь поговорить о следующем возможном шаге в теории машинного обучения. А следующий докладчик, Сергей Бартунов, попытается заняться деконструкцией мифа и в каком-то смысле продолжить мысль, что глубинное обучение — не панацея. Но Сергей подойдет к этому несколько с другой стороны, предоставит некий более глобальный взгляд.

Итак, что же такое байесовский подход? Весь подход базируется на одной единственной формуле или теореме. Теорема Байеса приведена в математической и концептуальной формах.
Ключевая идея. Предположим, есть какая-то неизвестная величина, которую мы бы хотели оценить по каким-то ее косвенным проявлениям. В данном случае неизвестная величина — ?, а ее косвенное проявление — у. Тогда можно воспользоваться теоремой Байеса, которая позволяет наше исходное незнание или знание о неизвестной величине, априорное знание, трансформировать в апостериорное после наблюдения некоторых косвенных характеристик, как-то косвенно характеризующих неизвестную величину ?.
Ключевая особенность формулы — в том, что на вход мы подаем априорное распределение, кодирующее наше незнание или нашу неопределенность о неизвестной величине, и что выходом также является распределение. Это крайне важный момент. Не точечная оценка, а некая сущность того же формата, что был на входе. Благодаря этому становится возможным, например, использовать результат байесовского вывода, апостериорное распределение, как априорное в какой-то новой вероятностной модели и, таким образом, охарактеризовать новую неизвестную величину с разных сторон путем анализа ее различных косвенных проявлений. Это первое достоинство, благодаря которому удается получить свойство расширяемости — или композицируемости — разных вероятностных моделей, когда мы можем из простых моделей строить более сложные.
Второе интересное свойство. Простейшее правило суммирования произведения вероятностей означает: если у нас есть вероятностная модель — а другими словами, совместное вероятностное распределение на все переменные, возникающие в нашей задаче, — то мы, как минимум в теории, всегда можем построить любой вероятностный прогноз, спрогнозировать интересующую нас переменную U, зная какие-то наблюдаемые переменные О. При этом есть переменная L, которую мы не знаем и она нас не интересует. По этой формуле они отлично исключаются из рассмотрения.
Для любых сочетаний этих трех групп переменных мы всегда можем построить такое условное распределение, которое и укажет, как изменились наши представления об интересующих нас величинах U, если мы пронаблюдали величины О, предположительно связанные с U.

По сути, повсеместное применение формул Байеса дало рождение второму альтернативному подходу к теории вероятностей. Есть классический подход — на Западе нередко называемый частотным, фриквентистским, — и есть альтернативный байесовский подход. Вот краткая таблица, которую я привожу на всех своих лекциях и которая показывает различия между подходами. Естественно, они друг другу не противоречат. Они скорее друг друга дополняют. По этой табличке можно проследить, что у них общего и в чем различия.
Ключевое различие в том, что понимать под случайной величиной. В частотных терминах мы под случайной величиной понимаем величину, значение которой мы спрогнозировать не можем, не оценив какие-то статистические закономерности. Нужно что-то обладающее объективной неопределенностью, в то время как при байесовском подходе случайная величина интерпретируется просто в качестве детерминированного процесса. Он может быть полностью спрогнозирован. Просто в данном детерминированном процессе мы не знаем часть факторов, влияющих на исход. Поскольку мы их не знаем, мы не можем спрогнозировать исход детерминированного процесса. Значит, для нас данный исход выглядит как случайная величина.
Простейший пример — подбрасывание монетки. Речь идет о классической случайной величине, но мы понимаем, что монетка подчиняется законам классической механики и, вообще-то, зная все начальные условия — силу, ускорение, коэффициент сопротивления среды и т. д., — мы могли бы точно сказать, как монетка упадет: орлом или решкой.
Если вдуматься, подавляющее большинство величин, которые мы привыкли считать случайными, на самом деле случайны именно в байесовском смысле. Это какие-то детерминированные процессы, просто мы не знаем часть факторов этих процессов.
Поскольку один может не знать одни факторы, а другой — другие, возникает понятие субъективной неопределенности или субъективного незнания.
Остальное — прямые различия этой интерпретации. Все величины в байесовском подходе можно трактовать как случайные. Аппарат теории вероятностей применяется к параметрам распределения случайной величины. Другими словами, то, что в классическом подходе бессмысленно, в байесовском подходе обретает смысл. Метод статистического метода, вместо метода максимального правдоподобия — теорема Байеса. Оценки получаем не точечные, а вида апостериорного распределения, позволяющего нам комбинировать разные вероятностные модели. И в отличие от частотного подхода — теоретически обоснованного при больших n, а некоторые доказывают, например, при n, стремящихся к бесконечности, — Байесовский подход верен при любых объемах выборки, даже если n = 0. Просто в данном случае апостериорное распределение совпадет с априорным.

Простая иллюстрация. Известная притча о слепых мудрецах и слоне, показывающая, как модель можно зацепить.
Давайте представим: дано несколько слепых мудрецов и один слон. Задача — оценить массу этого слона. Мудрецы знают, что сейчас будут щупать некое животное. Какое именно — не знают, но они должны оценить массу.

Они все начинают с того, что кодируют свои представления о возможной массе животного в виде априорного распределения, поскольку теперь плотность распределения может определять простую меру нашего незнания о чем-то. Для кодирования указанных знаний мы можем просто использовать аппарат теории вероятностей.
Поскольку речь идет о мудрецах, они знают характерные массы животных на планете Земля. Поэтому они и получают примерно такое априорное распределение.
Первый мудрец подходит, щупает хвост и делает вывод, что, видимо, перед ним нечто змееобразное либо хвост крупного животного. Значит, в процессе своего байесовского вывода, объединив результаты своих представлений, которые можно выразить в виде вероятностной подели p1, он получает апостериорное распределение р(?) при условии х=1.
Дальше подходит другой мудрец, который может не щупать, а скажем, нюхать. Тут абсолютно другая модель. X2 — это величина совершенно из другого домена, косвенно характеризующая массу животного. В процессе своего байесовского вывода он использует в качестве априорного распределения не исходное, с которого все начинали, а результат вывода предыдущего мудреца. Тем самым мы можем объединить два совершенно различных измерения, два источника информации, в одной элегантной вероятностной модели.
И вот, проделав серию измерений, мы в конечном итоге получаем уже достаточно острое апостериорное распределение, почти точную оценку. Мы уже с высокой точностью можем сказать, какая масса была у животного. Это иллюстрация к третьему свойству — к extendibility, то есть к возможности модели всё время расширять и зацеплять.
Другое достоинство байесовского подхода, уже применительно к машинному обучению, — регуляризация. Благодаря учету априорных предпочтений мы препятствуем излишней настройке наших параметров в ходе процедуры машинного обучения и тем самым способны справляться с эффектом переобучения. Какое-то время назад, когда алгоритмы начали обучать на огромных объемах данных, считалось, что проблема переобучения снята с повестки дня. Но дело было исключительно в том, что люди психологически боялись переходить к нейросетям гигантского размера. Все начинали с небольших нейросетей, и они, при гигантских обучающих выборках, действительно не переобучались. Но по мере того, как психологический страх исчезал, люди начинали использовать сети всё большего размера.
Стали очевидными две вещи. Для начала — чем больше сеть, тем она в принципе лучше. Большие сети работают лучше, чем маленькие. Но большие сети начинают переобучаться. Если у нас количество параметров — 100 млн, то 1 млрд объектов — не очень большая обучающая выборка, и нам необходимо регуляризовывать процедуру такого машинного обучения.
Байесовский подход как раз дает прекрасную возможность делать это за счет введения априорного распределения на те параметры, на те веса нейронной сети, которые настраиваются в ходе процедуры обучения.
В частности, оказалось, что такая популярная техника эвристической регуляризации, как drop out, является частным случаем, грубым приближением для байесовской регуляризации. На самом деле речь идет о попытке сделать байесовский вывод.
Наконец, третье преимущество — возможность построения модели с латентными переменными. О ней подробнее.

У нас есть мотивирующий пример — метод главных компонент. Метод очень простой — линейное уменьшение размерности. Берем выборку в пространстве с высокой размерностью, строим ковариационную матрицу, проецируем на главную ось с соответствующим самым большим значением. Вот что геометрически здесь показано. И уменьшили размерность пространства с 2 до 1, сохранив максимум дисперсии, содержавшейся в выборке.
Метод простой, допускает решение в явном виде. Но можно альтернативно сформулировать иначе, в терминах вероятностной модели.

Представим, что наши данные устроены так: для каждого объекта есть его скрытое представление в пространстве маленькой размерности. Здесь оно обозначено как z. А мы наблюдаем линейную функцию от этого скрытого представления в пространстве с более высокой размерностью. Мы взяли линейную функцию и дополнительно добавили нормальный шум. Тем самым мы получили х, высокоразмерные данные, по которым нам крайне желательно восстановить их низкоразмерное представление.

Математически это выглядит так. Мы задали вероятностную модель, которая является совместным вероятностным распределением на наблюдаемые и скрытые компоненты, на x и z. Модель достаточно простая, выборка характеризуется произведением по объектам. Наблюдаемая компонента каждого объекта определяется скрытой компонентой, речь идет об априорном распределении на скрытой компоненте. И то и другое является нормальным распределением. Мы предполагаем, что в малоразмерном пространстве данные распределены априорно нормально, и наблюдаем линейную функцию этих данных, которая зашумлена нормальным шумом.
Нам задана выборка, представляющая собой высокоразмерное представление. Мы знаем x, мы не знаем z, и наша задача — найти параметр ?. ? — это матрица V, ?? и всё.
Указанную задачу можно сформулировать на байесовском языке как задачу обучения с латентными переменными. Чтобы применить обычный метод максимального правдоподобия, не хватает знания увеличения z. Оказывается, для этой техники существует стандартный подход, основанный на ЕМ-алгоритме и различных модификациях. Можно запустить итерационный процесс. На ЕМ-шаге приведены формулы, описывающие, что мы делаем. Можно теоретически показать, что процесс монотонный и гарантированно сходится к локальному экстремуму, но все-таки.
Возникает вопрос: а зачем нам применять итерационный процесс, когда мы знаем, что задача решается в явном виде?
Ответ простой. Для начала — алгоритмическая сложность. Сложность аналитического решения — O(nD?), в то время как сложность одной итерации ЕМ-алгоритма — O(nDd).
Если мы мысленно представим, что проецируем пространство размерностью 1 млн в пространство размерностью 10, и ЕМ-алгоритм сходится итераций за сто, то наша итерационная схема будет работать в 1000 раз быстрее, чем решение в явном виде.
Кроме того, важное достоинство: теперь мы нашу базовую модель, метод главных компонент, можем различными способами расширять в зависимости от специфики конкретной задачи. Например, мы можем ввести понятие смеси методов главных компонент, и сказать, что наши данные живут не в одном пространстве, линейном подпространстве меньшей размерности, а в нескольких. И мы не знаем, из какого подпространства пришел каждый конкретный объект.
Возникает смесь методов главных компонент. Формально модель записывается так. Просто ввели дополнительную номенклатуру скрытых дискретных переменных t. И опять же, ЕМ-алгоритм позволяет нам найти решение задачи почти по тем же формулам, хотя исходный метод главных компонент нам не позволял производить никакие модификации.

Еще одно — возможность работать в ситуациях, когда, допустим, для нашей выборки часть компонент х неизвестны, данные пропущены. Бывает такое? Сплошь и рядом. Несколько более экзотическая ситуация — когда нам известны скрытые представления части объектов, низкоразмерное представление, целиком или частично. Но опять же, такая ситуация возможна.
исходная модель метода главных компонент не способна учесть ни того, ни другого, в то время как вероятностная модель, сформулированная на байесовском языке, и то, и другое учитывает элементарно — простой модификацией ЕМ-алгоритма. Мы просто немного меняем номенклатуру наблюдаемых скрытых переменных.
Тем самым мы можем решать задачи обработки данных, когда какие-то произвольные фрагменты этих данных могут отсутствовать, не то что в стандартном машинном обучении, когда выделяется номенклатура наблюдаемых и как бы скрытых, целевых переменных и перемешиваться они никак не могут. Здесь возникает дополнительная гибкость.

Наконец, до недавнего времени считалось, что существенное ограничение байесовских методов состоит в том, что они, обладая высокой вычислительной сложностью, применимы к небольшим выборкам данных и не переносятся на большие данные. Результаты последних нескольких лет показывают, что это не так. Человечество наконец-то научилось обеспечивать масштабируемость байесовских методов. И люди тут же начали скрещивать байесовские методы с глубинными нейронными сетями.
О том, как масштабировать байесовский метод, я скажу пару слов, благо время еще есть.

Теорема Байеса. Хотим по известным X, M сказать что-то про Z, который как-то связан с X. Мы применяем теорему Байеса. Вопрос: какое здесь самое уязвимое место, какой самый тяжелый фргамент? Интеграл.
В тех редких случаях, когда интеграл берется аналитически, все хорошо. Другое дело, если он аналитически не берется — а ведь мы представляем, что говорим о высокоразмерных данных, и тут интеграл в пространстве размерностью не 1 или 2, а десятки и сотни тысяч.
С другой стороны, давайте запишем цепочку. Стартуем: ? p(X|Z) p(Z) dZ. Поскольку log P(X) dZ не зависит, это просто интеграл по всему Z, равный 1.
Второе действие. Выразили p(X), по этой формуле перенесли влево, p(Z|X) в знаменатель, записали под интегралом.
Теперь у нас числитель и знаменатель зависят от Z, хотя их частное дает p(X), то есть не зависит от Z. Тождество.
Дальше умножили то, что стоит под log, умножили на 1 и поделили на q(Z).
И последнее — разбили интеграл на две части. Тут видим: вторая часть — хорошо известная в теории вероятностей дивергенция Кульбака-Лейблера, величина неотрицательная и равная нулю тогда и только тогда, когда эти два распределения совпадают между собой. В каком-то смысле это аналог расстояния между распределениями. А напоминаю, наша задача оценить p(Z|X) хотя бы приближенно, выполнить байесовский вывод.
Эту величину мы посчитать не можем, здесь фигурирует p(Z|X). Зато отлично можем посчитать первое слагаемое. Каждое из слагаемых зависит от q(Z), но их сумма от q(Z) не зависит, потому что она равна log p(X). Возникает идея: а давайте мы будем первое слагаемое максимизировать по q(Z), по распределению.
Это означает, что, максимизируя первое слагаемое, мы минимизируем второе — которое показывает степень приближения q(Z) к истинному апостериорному распределению. И вот, тем самым, ключевая идея: мы свели задачу байесовского вывода, включающую в себя интегрирование в пространстве высокой размерности, к задаче оптимизации.
Задачу оптимизации человечество умеет решать хорошо даже при гигантских объемах данных.

Такой подход называется вариационный Байес. Ключевая идея — что вывод становится оптимизацией.
Какие у нас есть универсальные анализаторы, аппроксиматоры? Особенно пригодные для работы с большими данными? Нейронные сети.
Про стохастическую оптимизацию не успеваю сказать.

Здесь я уже сделал следующий шаг — обучение по неполной разметке. Дано Xtr, Z мы не знаем, и нам бы оптимизировать этот функционал по ?. Мы даже не можем его в явном виде посчитать, но зато, когда мы заменили его на вариационную нижнюю оценку L, появилась еще и зависимость от ? — поскольку мы хотим дополнительно левую часть оптимизировать по ?. Мы можем оптимизировать L одновременно по Q(Z) и по ?. Оптимизация по ? позволяет нам всё лучше описывать обучающую выборку, а оптимизация по Q(Z) позволяет всё точнее проводить байесовский вывод над скрытыми переменными Z.
Среди прочего оказывается, что такая модель допускает эффективную оптимизацию с помощью методов стохастической оптимизации. Они позволяют оптимизировать функцию, которую мы, может, даже не сможем посчитать ни в одной точке. Нам достаточно уметь считать для нее стохастический градиент и, быть может, какие-то дополнительные характеристики для дальнейшего ускорения сходимости.
Здесь оказывается, что никаких проблем нет. Стохастический градиент для вариационной нижней оценки может быть выражен по такой формуле, где мы сгенерировали Z из текущего Q(Z). Ну и всё, дальше можно дифференцировать. Тут есть некоторые тонкости, но о них я рассказать уже не успею.

По поводу того, как уменьшать дисперсию стохастического градиента. Нейробайесовский подход родился в тот момент, когда мы поняли, как эту дисперсию можно уменьшить, — потому что затем стало возможным применять байесовские техники в глубинном обучении и, как следствие, успешно решать новый спектр задач.
Расскажу об одной из них. Речь идет о вариационном автокодировщике — он представляет собой сравнительно прямолинейное обобщение методов главных компонент в его байесовской интерпретации. Вспоминаем: наверху формула для методов главных компонент. Есть скрытые переменные, априорно имеющие нормальное распределение в пространстве маленькой размерности, и есть наблюдаемые компоненты, которые просто являются линейной функцией от скрытых компонент. Плюс нормальный шум.
Казалось бы, давайте сделаем всё то же самое, только пусть будет не линейная функция, а что-нибудь более хитрое. Здесь так и сделано, ? и ? — теперь не линейные функции от латентного представления данного объекта. Пусть это будет выходом нейронной сети. Есть нейронная сеть, которая на вход получает Zi и выдает значение ? и ?, которое показывает распределение соответствующего Xi. Данная нейронная сеть имеет веса ?. В остальном модель та же самая. Единственное, мы вместо линейной функции поставили сюда нелинейную, определяемую нейронной сетью.

Всё бы хорошо, но проблема в следующем: в этой задаче строгий байесовский вывод, в отличие от метода главных компонент, уже сделать нельзя. Поэтому здесь приходится использовать ту вариационную технику, о которой я рассказал раньше. Мы переходим к вариационной оценке L, вводим распределение Q(Z), которое параметризуется через ?, и пусть это будет другая нейронная сеть. Чем богаче семейство распределений, где мы проводим оптимизацию, тем лучше. Самое богатое, что мы умеем оптимизировать на сегодняшний день, — нейронные сети, обладающие достаточной гибкостью.
Добавим вспомогательную нейронную сеть. У нее будут свои параметры ?. Сеть, которая принимает Z, возвращает X. Эта сеть — наоборот, принимает X и возвращает распределение на Z.
Такая техника очень похожа на то, что в нейронных сетях известно как модель автокодировщика. Только здесь все сформулировано на вероятностном языке, поэтому ее назвали вариационным автокодировщиком.

Для начала оказалось, что такая модель может быть обучена крайне эффективно. Значит, ее можно обучать на гигантских выборках данных. Чем больше выборки, тем выше качество аппроксимации и тем лучше мы решаем задачу уменьшения размерности, поиска низкоразмерных латентных представлений, выучивания представлений. В глубинном обучении их называют representations.
Одновременно мы оптимизируем нижнюю оценку на этот log и, по сути, восстанавливаем плотность в пространстве иксов. Как правило, пространство иксов является высокоразмерным — скажем, пространством изображений, видеозаписей, анкет пользователей социальной сети, некоторых объектов со сложной природой — и восстановить плотность в нем довольно проблематично. Но — возможно с помощью техники вариационного автокодировщика. Она была предложена приблизительно полтора-два года назад и казалась настолько успешной, что с тех пор появилось огромное количество модификаций, позволяющих учитывать априорные представления о структурах пространства, о латентных переменных, комбинировать эту технику с графическими моделями и т. д. Указанная область сейчас развивается взрывными темпами, и перед нами один из примеров того, как байесовские методы и, по сути, байесовский вывод были применены к задаче глубинного обучения. В данном случае глубинное обучение используется для уменьшения размерности пространства.
Это один из примеров, но далеко не единственный. Другой пример из известных мне — байесовское обоснование процедуры drop out. Исходно она была придумана инженерами для инженеров, и никто не мог членораздельно объяснить, почему она работает. Теперь мы знаем, почему. Мы знаем, что там задействован байесовский регуляризатор специального вида. Никто не мешает нам использовать другой регуляризатор и получить немного другую процедуру. Теперь мы можем не использовать drop out как черный ящик, как некую фиксированную процедуру, а модифицировать его в разные стороны, понимая, что лежало в основе этой процедуры.
Кроме того, в прошлом году была предложена техника карт внимания, attention maps, которая тоже позволила существенно расширить класс задач, решаемых нейронными сетями. Для начала речь идет о задачах генерации текста по изображению. В основе такой техники лежит вариационный байесовский вывод некоторого специального вида, но по сути — тоже базирующийся на оптимизации некоторой эволюционной оценки L(Q|?).
На этом закончу. Резюмируя, выскажу две ключевые мысли. Байесовский подход прекрасно комбинируется, и на наших глазах происходит все больше работ в этом направлении. Скажем, на главной конференции по машинному обучению NIPS аж четыре воркшопа, посвященных байесовским методам, и часть воркшопов — как раз по их скрещиванию с нейронными сетями.
Надеюсь, мне удалось донести преимущества байесовского подхода и сущность вариационного байесовского вывода, рассказать, благодаря чему байесовские методы удалось масштабировать и перенести на большие данные. А как мы дальше будем скрещивать и получать нейробайеса — увидим в ближайшие годы. Спасибо.
Поделиться с друзьями


yuri_ignatiev
Отличная статья, можно ещё добавить ссылки на примеры применения Байесовского подхода к обучению нейронных сетей.