Третий урок
Простой, казалось бы, вопрос: что такое векторное произведение. Вот даны два вектора a и b в обычном евклидовом трёхмерном пространстве. Мы знаем их длины, угол между ними и даже координаты в ортонормированном базисе (в декартовой системе координат). Но морально неподготовленного читателя даже с высшим математическим образованием может ждать маленький сюрприз: куда же направить вектор c = [a,b] — вверх или вниз? Вопрос чуть усложнится, если мы случайно вдруг взяли левую систему координат, например с недосыпу перепутав первые два базисных вектора: {ey,ex,ez}.
Тройка векторов a,b,c = [a,b] должна быть правой. А величина вектора c равна… тра-та-та…
Этим наглядным определением неудобно пользоваться при числовых расчетах. К тому же такое определение не всегда совпадает с нижеследующим.
Тройка векторов должна быть такой же как базис.

Этому определению безразличны и правая и левая системы координат: если записали матрицу, где в строчках у Вас координаты векторов, то всё — «определитель» даст Вам третий вектор однозначно. И эти три вектора ориентированы будут не обязательно по-правому, а точно также, как базис.
Векторное произведение через Символ Леви-Чевиты
Всё в нашей власти. Как определим, так и будет. В правом базисе это вообще без разницы, и прекратите пудрить мозги.
Есть у «физиков» (в теоретической физике это придумали, чтоб жизнь была веселее) такие тёмные штуки, как истинные векторы и псевдовекторы, которые очень похожи. Но их можно отличить по тому, как они реагируют на инверсию. Истинные векторы, при слове «инверсия», резко умножаются на «минус один», а псевдовекторы ничего не делают. Причем неважно какую инверсию Вы имели ввиду: активную или пассивную. Все равно, формально это выглядит как умножение координат на «минус один».
Напомним из прошлого урока про инверсию: это такая операция по выворачиванию трехмерного пространства в зазеркалье. Инверсия по отношению ко всем векторам бывает двух видов:
— активная — истинный вектор активно разворачивается носом на зад, а базисные векторы остаются как были;
— пассивная — истинный вектор пассивно висит в воздухе, но носы разворачивают базисные векторы, превращаясь по ходу из правой тройки в левую (псевдовекторы при пассивной инверсии, имейте ввиду, тоже крутятся).
— При чем тут эти псевдоштуки?! — законно спросите Вы. Дело в том, что если два истинных вектора перемножить векторно, то получится псевдовектор. Ну хочется так «физикам», вот они и определение векторного произведения под это дело подогнали.
Короче, было бы очень хорошо для «физиков» с их псевдовекторами, если тройка векторов всегда будет правой и не зависеть от ориентации базиса.
— Давайте, — говорят «физики», — следить за базисом, и если он станет левым, то мы символ Леви-Чевиты немножко переопределим: скажем чтоб первый элемент равнялся «минус один», или две строки в матрице поменяем… или просто ничего такого делать не будем, а умножим результат на «минус один» — для левого базиса это всё едино.
1. На вопрос «Это шо же?! Векторное произведение может зависеть от правоты-левоты базиса?!» спокойно можно отвечать: «Ну а чо такого?»
2. — Как же так?! — спросите Вы. И будете правы. Мы же давно привыкли, что уже давно как-то всё определено. Вот про слово «определение» и хотелось бы сказать. Смотрите. Всё начинается с определения. Например «векторное произведение». Вы можете сами его определить, сами можете придумать правило, как из двух векторов сделать один. Вопрос только в том, зачем Вам это. В чем польза такого Вашего определения? Зачем Вам такая операция? Ну если Вам полезно, то можно никого даже не слушать, кто возмущается Вашим определением. Да, это будет другое определение, не такое как у всех. Да, когда Вы будете говорить слова «векторное произведение» все будут думать что-то своё, а Вы — своё. Да, это наверное окажется неудобно, если Вам хочется поговорить о своем полезном и нужном «векторном произведении». Словами «векторное произведение» Вы можете обозначить какую-то свою секретную операцию и это будет неудобно. Вот пожалуй единственная причина, что так не делать — удобство общения: лучше бы договариваться об одних и тех же обозначениях.
3. Собственно о векторном произведении. Так получилось, что не договорились люди про него. Не все договорились. В некоторых книжках встречается свой собственный самобытный взгляд автора на векторное произведение. Ну чтоб голословным не быть, приведу один пример. В книжке «Векторное исчисление и начала тензорного исчисления» автор Кочин Н. Е. хочет, чтоб ориентация тройки a, b, [a,b] совпадала с ориентацией базиса. (издание девятое, 1965 года, стр.44, фиг. 27).
4. Давайте поверим тем людям, которые хотят, чтоб тройка векторов: a, b, [a,b] была правой всегда, независимо от системы координат. Чтоб векторное произведение не зависело от ориентации базиса. Удобное определение: псевдовекторы и истинные векторы ведут себя хорошо при пассивной инверсии (если мы людям не поверим, и будем пользоваться определением Кочина Н.Е., то плохо будут вести себя псевдовекторы в левой СК). Так вот. Эти люди в векторном произведении будут зорко следить, что, как только попадется левый базис, то они сразу скажут первой компоненте символа Леви-Чевиты, что она равна не «плюс один», а «минус один». Эти люди, если будут вычислять векторное произведение через определитель, то в левом базисе они заботливо умножат на «минус один» свой вектор. А другие, которые не в курсе — они следить не будут, у них результирующий вектор будет смотреть в другую сторону.
5. И еще одна тонкость. Вот я не нарисовал никакого рисунка, а просто сказал: «тройка векторов a, b, c — правая». Вы мне верите без рисунка? Напрасно не верите. Это и есть определение. Больше ничего не нужно для алгоритма. Ничего больше не нужно для всего математического аппарата. Надо один раз твердо сказать — «вот это вот, вот эти три вектора я назову правым базисом». Могу добавить еще, как бы добивая всех вокруг, что он у меня ортогонален (что все векторы под прямыми углами) и отнормирован (у всех единичная, одинаковая длина) — и никто не сможет поспорить — это и есть определение. Смешно, но правда. А рисунок — вторичен. Всё, что соединяет мои слова с рисунком — это Ваша правая рука. Научили бы Вас в детстве родители неправильно, перепутали бы Вам руки, и Вы рисовали бы наоборот: я просил бы нарисовать Вас правую тройку, а Вы рисовали бы мне левую. И мы бы все вместе волновались и спорили, кто прав: Ваши родители или мои. То же самое касается и понятия «псевдовектора». Надо тупо назначить любые два вектора истинными. Вот так вот торжественно: «Нарекаю векторы ф и ы с координатами в моем правом ортонормированном базисе (который a, b, c) — истинными векторами». Тогда результат их векторного произведения будет псевдовектором.
Есть такое слово: «дельта». Ну это приращение какой-нибудь величины. Так вот обозначений этих дельт бывает несколько. Например: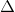 ,
,  ,
,  ,
, 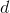 . Как вы думаете, зачем столько букв?
. Как вы думаете, зачем столько букв?
Конец третьего урока. Продолжение следует.
Вопрос о векторном произведении
Простой, казалось бы, вопрос: что такое векторное произведение. Вот даны два вектора a и b в обычном евклидовом трёхмерном пространстве. Мы знаем их длины, угол между ними и даже координаты в ортонормированном базисе (в декартовой системе координат). Но морально неподготовленного читателя даже с высшим математическим образованием может ждать маленький сюрприз: куда же направить вектор c = [a,b] — вверх или вниз? Вопрос чуть усложнится, если мы случайно вдруг взяли левую систему координат, например с недосыпу перепутав первые два базисных вектора: {ey,ex,ez}.
Вот какие у нас могут быть ответы
Ответ 1 (геометрическое определение векторного произведения)
Тройка векторов a,b,c = [a,b] должна быть правой. А величина вектора c равна… тра-та-та…
Этим наглядным определением неудобно пользоваться при числовых расчетах. К тому же такое определение не всегда совпадает с нижеследующим.
Ответ 2 (алгебраическое определение через определитель матрицы)
Тройка векторов должна быть такой же как базис.

Этому определению безразличны и правая и левая системы координат: если записали матрицу, где в строчках у Вас координаты векторов, то всё — «определитель» даст Вам третий вектор однозначно. И эти три вектора ориентированы будут не обязательно по-правому, а точно также, как базис.
Ответ 3 (тензорное определение)
Векторное произведение через Символ Леви-Чевиты
Ответ 4 (математический)
Всё в нашей власти. Как определим, так и будет. В правом базисе это вообще без разницы, и прекратите пудрить мозги.
Ответ 5 («физический»)
Есть у «физиков» (в теоретической физике это придумали, чтоб жизнь была веселее) такие тёмные штуки, как истинные векторы и псевдовекторы, которые очень похожи. Но их можно отличить по тому, как они реагируют на инверсию. Истинные векторы, при слове «инверсия», резко умножаются на «минус один», а псевдовекторы ничего не делают. Причем неважно какую инверсию Вы имели ввиду: активную или пассивную. Все равно, формально это выглядит как умножение координат на «минус один».
Напомним из прошлого урока про инверсию: это такая операция по выворачиванию трехмерного пространства в зазеркалье. Инверсия по отношению ко всем векторам бывает двух видов:
— активная — истинный вектор активно разворачивается носом на зад, а базисные векторы остаются как были;
— пассивная — истинный вектор пассивно висит в воздухе, но носы разворачивают базисные векторы, превращаясь по ходу из правой тройки в левую (псевдовекторы при пассивной инверсии, имейте ввиду, тоже крутятся).
— При чем тут эти псевдоштуки?! — законно спросите Вы. Дело в том, что если два истинных вектора перемножить векторно, то получится псевдовектор. Ну хочется так «физикам», вот они и определение векторного произведения под это дело подогнали.
Короче, было бы очень хорошо для «физиков» с их псевдовекторами, если тройка векторов всегда будет правой и не зависеть от ориентации базиса.
— Давайте, — говорят «физики», — следить за базисом, и если он станет левым, то мы символ Леви-Чевиты немножко переопределим: скажем чтоб первый элемент равнялся «минус один», или две строки в матрице поменяем… или просто ничего такого делать не будем, а умножим результат на «минус один» — для левого базиса это всё едино.
Мораль
1. На вопрос «Это шо же?! Векторное произведение может зависеть от правоты-левоты базиса?!» спокойно можно отвечать: «Ну а чо такого?»
2. — Как же так?! — спросите Вы. И будете правы. Мы же давно привыкли, что уже давно как-то всё определено. Вот про слово «определение» и хотелось бы сказать. Смотрите. Всё начинается с определения. Например «векторное произведение». Вы можете сами его определить, сами можете придумать правило, как из двух векторов сделать один. Вопрос только в том, зачем Вам это. В чем польза такого Вашего определения? Зачем Вам такая операция? Ну если Вам полезно, то можно никого даже не слушать, кто возмущается Вашим определением. Да, это будет другое определение, не такое как у всех. Да, когда Вы будете говорить слова «векторное произведение» все будут думать что-то своё, а Вы — своё. Да, это наверное окажется неудобно, если Вам хочется поговорить о своем полезном и нужном «векторном произведении». Словами «векторное произведение» Вы можете обозначить какую-то свою секретную операцию и это будет неудобно. Вот пожалуй единственная причина, что так не делать — удобство общения: лучше бы договариваться об одних и тех же обозначениях.
3. Собственно о векторном произведении. Так получилось, что не договорились люди про него. Не все договорились. В некоторых книжках встречается свой собственный самобытный взгляд автора на векторное произведение. Ну чтоб голословным не быть, приведу один пример. В книжке «Векторное исчисление и начала тензорного исчисления» автор Кочин Н. Е. хочет, чтоб ориентация тройки a, b, [a,b] совпадала с ориентацией базиса. (издание девятое, 1965 года, стр.44, фиг. 27).
4. Давайте поверим тем людям, которые хотят, чтоб тройка векторов: a, b, [a,b] была правой всегда, независимо от системы координат. Чтоб векторное произведение не зависело от ориентации базиса. Удобное определение: псевдовекторы и истинные векторы ведут себя хорошо при пассивной инверсии (если мы людям не поверим, и будем пользоваться определением Кочина Н.Е., то плохо будут вести себя псевдовекторы в левой СК). Так вот. Эти люди в векторном произведении будут зорко следить, что, как только попадется левый базис, то они сразу скажут первой компоненте символа Леви-Чевиты, что она равна не «плюс один», а «минус один». Эти люди, если будут вычислять векторное произведение через определитель, то в левом базисе они заботливо умножат на «минус один» свой вектор. А другие, которые не в курсе — они следить не будут, у них результирующий вектор будет смотреть в другую сторону.
5. И еще одна тонкость. Вот я не нарисовал никакого рисунка, а просто сказал: «тройка векторов a, b, c — правая». Вы мне верите без рисунка? Напрасно не верите. Это и есть определение. Больше ничего не нужно для алгоритма. Ничего больше не нужно для всего математического аппарата. Надо один раз твердо сказать — «вот это вот, вот эти три вектора я назову правым базисом». Могу добавить еще, как бы добивая всех вокруг, что он у меня ортогонален (что все векторы под прямыми углами) и отнормирован (у всех единичная, одинаковая длина) — и никто не сможет поспорить — это и есть определение. Смешно, но правда. А рисунок — вторичен. Всё, что соединяет мои слова с рисунком — это Ваша правая рука. Научили бы Вас в детстве родители неправильно, перепутали бы Вам руки, и Вы рисовали бы наоборот: я просил бы нарисовать Вас правую тройку, а Вы рисовали бы мне левую. И мы бы все вместе волновались и спорили, кто прав: Ваши родители или мои. То же самое касается и понятия «псевдовектора». Надо тупо назначить любые два вектора истинными. Вот так вот торжественно: «Нарекаю векторы ф и ы с координатами в моем правом ортонормированном базисе (который a, b, c) — истинными векторами». Тогда результат их векторного произведения будет псевдовектором.
Задание на дом
Есть такое слово: «дельта». Ну это приращение какой-нибудь величины. Так вот обозначений этих дельт бывает несколько. Например:
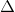 ,
,  ,
,  ,
, 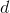 . Как вы думаете, зачем столько букв?
. Как вы думаете, зачем столько букв? Конец третьего урока. Продолжение следует.
Поделиться с друзьями
Комментарии (2)

koldyr
17.04.2017 22:01Каноническое определение у Кочина. Пространства могут быть отличной от 3 размерности. И везде будет одно и тоже — произвол в выборе положительной ориентации.


QDeathNick
Если вам интересно, моё мнение: На слух, с эмоциями и мимикой лектора, этот текст может быть ещё как-то будет восприниматься, но читать такую прямую речь мне очень тяжело, какая-то каша.