12.04.2017 04:25
FransuaMaryDelone 35 9700 Источник

Как-то мне понадобилась "собственная мода оптоволокна". Но я нигде не нашел аналитического выражения электромагнитного поля. Ну и «сделал сам», раз не нашел, и оформил для всех тут, в статье. Так что, скорее всего, нигде больше вы такого не встретите — уникальнейшая вещь! В книжках это не пишут, потому что оно длинное — обычно пишут самое простое, а про общий случай упоминают вскользь. Ну вот он, общий случай, под катом.

Постановка задачи



Решить уравнения Максвелла с условиями:

— оптоволокно состоит из сердцевины радиуса $a$ с диэлектрической проницаемостью $\varepsilon_1$ и оболочки бесконечного внешнего радиуса с диэлектрической проницаемостью $\varepsilon_2$,
— поле периодично по $z$, пространственная частота всех компонент поля едина: $k_z$,
— компоненты поля на оси $O_z$ — без особенностей,
— компоненты поля при $r \rightarrow\infty$ интегрируемы с квадратом,
— тангенциальные компоненты поля на поверхности цилиндра $r=a$ — непрерывны:

$E_{z,1}\bigg|_{r=a}=E_{z,2}\bigg|_{r=a},$

$E_{\varphi,1}\bigg|_{r=a}=E_{\varphi,2}\bigg|_{r=a},$

$H_{z,1}\bigg|_{r=a}=H_{z,2}\bigg|_{r=a},$

$H_{\varphi,1}\bigg|_{r=a}=H_{\varphi,2}\bigg|_{r=a}$



1. Преобразование уравнений Максвелла, вызванное периодичностью по $z$


Подставив в уравнения Максвелла периодическую зависимость по $z$:

$\textbf{E}(x,y,z,t) = \left( \begin{array}{c} e_x(x,y)\\ e_y(x,y)\\ e_z(x,y) \end{array} \right) \exp\left\lbrace ik_zz - i\omega t \right\rbrace, \quad \textbf{B}(x,y,z,t) = \left( \begin{array}{c} b_x(x,y)\\ b_y(x,y)\\ b_z(x,y) \end{array} \right) \exp\left\lbrace ik_zz - i\omega t \right\rbrace,$


получаются уравнения на $z$-компоненты поля:

$\Delta_{\bot}e_z + \gamma^2e_z=0,\,\Delta_{\bot}b_z + \gamma^2b_z=0,\,\text{где }\Delta_{\bot}=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2},\quad \gamma^2 = \varepsilon\mu\frac{\omega^2}{c^2}-k^2_z.$


При этом остальные компоненты выражаются через $z$-компоненты по закону:

$\textbf{b}_{\bot} = \frac{i}{\gamma^2}\left\lbrace k_z \operatorname{grad}_{\bot}b_z + \varepsilon\mu\frac{\omega}{c}\left[ \hat{\textbf{z}}\times\operatorname{grad}_{\bot}e_z\right] \right\rbrace, \, \textbf{e}_{\bot} = \frac{i}{\gamma^2}\left\lbrace k_z \operatorname{grad}_{\bot}e_z - \frac{\omega}{c}\left[ \hat{\textbf{z}}\times\operatorname{grad}_{\bot}b_z\right] \right\rbrace,$


где $\hat{\textbf{z}}$ — единичный вектор вдоль оси $O_z$, $\operatorname{grad}_{\bot} = \hat{\textbf{x}} \partial_x+\hat{\textbf{y}}\partial_y$, $\textbf{e}_{\bot} = \hat{\textbf{x}}e_x + \hat{\textbf{y}} e_y,\,\textbf{b}_{\bot} = \hat{\textbf{x}}b_x +\hat{\textbf{y}}b_y$.

2. Уравнения на $z$-компоненты в полярных координатах


Уравнения на $e_z,\,b_z$ имеют один вид, решения одинаковы, поэтому естественно переобозначение искомой функции:

$\Delta_{\bot}\psi + \gamma^2\psi=0.$


В полярных координатах уравнение имеет вид:

$r^2\frac{\partial^2}{\partial r^2}\psi + r\frac{\partial}{\partial r}\psi + \frac{\partial^2 }{\partial \varphi^2}\psi + r^2\left( \frac{\varepsilon\mu}{c^2}\omega^2 - k_z^2 \right) \psi = 0.$



3. Разделение переменных в уравнении


Подстановкой в уравнение зависимости $\psi(r,\varphi) = u(r)v(\varphi)$ переменные разделяются:

$\frac{1}{u(r)}r^2\frac{\partial^2}{\partial r^2}u(r) + \frac{1}{u(r)}r\frac{\partial}{\partial r}u(r) + r^2\left( \frac{\varepsilon\mu}{c^2}\omega^2 - k_z^2 \right) = - \frac{1}{v(\varphi)}\frac{\partial^2 }{\partial \varphi^2}v(\varphi).$


Обозначив константу равенства символом $\nu^2$ выписываются обе части равенства:

$$display$$- \frac{1}{v(\varphi)}\frac{\partial^2 }{\partial \varphi^2}v(\varphi) = \nu^2,$$display$$

$\frac{1}{u(r)}r^2\frac{\partial^2}{\partial r^2}u(r) + \frac{1}{u(r)}r\frac{\partial}{\partial r}u(r) + r^2\left( \frac{\varepsilon\mu}{c^2}\omega^2 - k_z^2 \right) = \nu^2.$



4. Решение первого уравнения


Первое уравнение имеет решения: $v = С_1\exp\left\lbrace i\nu \varphi \right\rbrace$.

Из периодического граничного условия $v(\varphi)=v(\varphi+2\pi)$, следует, что $\nu$ — целое: $\exp\left\lbrace i\nu \varphi \right\rbrace=\exp\left\lbrace i\nu (\varphi+2\pi) \right\rbrace\rightarrow 1=\exp\left\lbrace i\nu2\pi \right\rbrace = \cos(2\pi\nu)+ i\sin(2\pi\nu) \Rightarrow$ $\Rightarrow\cos(2\pi\nu)=1, \sin(2\pi\nu)=0 \Rightarrow \nu =\ldots -2,-1,0,1,2\ldots$

5. Решение второго уравнения


Второе уравнение сводится либо к уравнению Бесселя, либо к модифицированному уравнению Бесселя:

1. Уравнение Бесселя:

$\rho_1^2\frac{d^2u}{d\rho_1^2} + \rho_1\frac{du}{d\rho_1} + (\rho_1^2 - \nu^2)u = 0,\text{ при }\rho_1 = r \sqrt{ \frac{\varepsilon_1\mu}{c^2}\omega^2 - k_z^2 },$


2. Модифицированное уравнение Бесселя:

$\rho_2^2\frac{d^2u}{d\rho_2^2} + \rho_2\frac{du}{d\rho_2} - (\rho_2^2 + \nu^2)u = 0,\text{ при }\rho_2 = r \sqrt{ k_z^2 - \frac{\varepsilon_2\mu}{c^2}\omega^2 }.$



Уравнению Бесселя удовлетворяют функции Бесселя $J_{\nu}(\rho_1)$ и функции Неймана $Y_{\nu}(\rho_1)$. Модифицированному уравнению Бесселя удовлетворяют функции Инфельда $I_{\nu}(\rho_2)$ и функции Макдональда $K_{\nu}(\rho_2)$.

В силу граничных условий: при $r=0$ — функция без особенностей, при $r=\infty$ — функция интегрируема с квадратом, при $r=a$ — тангенциальные компоненты поля непрерывны, — в качестве решения предлагается следующая комбинация: при $r < a$ — функция Бесселя $J_{\nu}(\rho_1)$, при $r > a$ — функция Макдональда $K_{\nu}(\rho_2)$.

Из предложенной комбинации следует, что сердцевина должна быть более оптически плотной, чем оболочка, $\varepsilon_1 > \varepsilon_2$:

$ \frac{\varepsilon_1\mu}{c^2}\omega^2 - k_z^2 > 0, \, k_z^2 - \frac{\varepsilon_2\mu}{c^2}\omega^2 > 0,$

$ \frac{\varepsilon_1\mu}{c^2}\omega^2 > k_z^2, \, k_z^2 > \frac{\varepsilon_2\mu}{c^2}\omega^2,$

$ \frac{\varepsilon_1\mu}{c^2}\omega^2 > \frac{\varepsilon_2\mu}{c^2}\omega^2,$

$ \varepsilon_1 > \varepsilon_2.$



6. Общий вид компонент $e_z,\,b_z$


Введя обозначения: $\gamma^2 = \frac{\varepsilon_1\mu_1}{c^2}\omega^2 - k_z^2, \, \kappa^2 = k_z^2 - \frac{\varepsilon_2\mu_2}{c^2}\omega^2,$ компоненты $e_z,\,b_z$ записываются в виде:

$e_{z,1} = A_eJ_{|\nu|}(\gamma r)\exp\left\lbrace i\nu \varphi \right\rbrace,\text{ при }r<a,$

$e_{z,2} = B_eK_{|\nu|}(\kappa r)\exp\left\lbrace i\nu \varphi \right\rbrace,\text{ при }r>a,$

$b_{z,1} = A_bJ_{|\nu|}(\gamma r)\exp\left\lbrace i\nu \varphi \right\rbrace,\text{ при }r<a, $

$b_{z,2} = B_bK_{|\nu|}(\kappa r)\exp\left\lbrace i\nu \varphi \right\rbrace,\text{ при }r>a. $


Здесь полагается, что $\nu =\ldots -2,-1,0,1,2\ldots$ (может принимать отрицательные значения), потому в индексах функций присутствует знак модуля (в уравнении Бесселя имеет место $\nu^2$, знак индекса предполагается неотрицательный). Далее знак модуля в индексах функций опускается, но подразумевается.

Кроме того, введен индекс для магнитной проницаемости: $\mu_1$ — в сердцевине, $\mu_2$ — в оболочке.

7. Соотношения на константы $A_e,\,A_b,\,B_e,\,B_b$


Используя закон

$\textbf{b}_{\bot} = \frac{i}{\gamma^2}\left\lbrace k_z \operatorname{grad}_{\bot}b_z + \varepsilon\mu\frac{\omega}{c}\left[ \hat{\textbf{z}}\times\operatorname{grad}_{\bot}e_z\right] \right\rbrace, \, \textbf{e}_{\bot} = \frac{i}{\gamma^2}\left\lbrace k_z \operatorname{grad}_{\bot}e_z - \frac{\omega}{c}\left[ \hat{\textbf{z}}\times\operatorname{grad}_{\bot}b_z\right] \right\rbrace,$

находятся компоненты $e_{\varphi,1},\,e_{\varphi,2},\,h_{\varphi,1},\,h_{\varphi,2}$, имея при этом в виду, что $\textbf{h}=\textbf{b}/\mu$.
Компоненты подставляются в граничное условие непрерывности тангенциальных компонент:

$e_{z,1}\bigg|_{r=a}=e_{z,2}\bigg|_{r=a},$

$e_{\varphi,1}\bigg|_{r=a}=e_{\varphi,2}\bigg|_{r=a},$

$h_{z,1}\bigg|_{r=a}=h_{z,2}\bigg|_{r=a},$

$h_{\varphi,1}\bigg|_{r=a}=h_{\varphi,2}\bigg|_{r=a}.$



Получается система линейных уравнений, суть соотношения на константы $A_e,\,A_b,\,B_e,\,B_b$, которая имеет вид:

$\left( \begin{array}{cccc} J_{\nu}(\gamma a) & -K_{\nu}(\kappa a) & 0 & 0 \\ 0 & 0 & \frac{1}{\mu_1}J_{\nu}(\gamma a) & -\frac{1}{\mu_2}K_{\nu}(\kappa a) \\ \frac{\nu k_z}{a\gamma^2} J_{\nu}(\gamma a) & \frac{\nu k_z}{a\kappa^2} K_{\nu}(\kappa a) & \frac{i}{\gamma^2}\frac{\omega}{c}\gamma J^{\prime}_{\nu}(\gamma a) & \frac{i}{\kappa^2} \frac{\omega}{c} \kappa K^{\prime}_{\nu}(\kappa a) \\ i\frac{\varepsilon\mu}{\gamma^2\mu_1}\frac{\omega}{c}\gamma J^{\prime}_{\nu}(\gamma a) & \frac{i}{\mu_2\kappa^2}\varepsilon\mu\frac{\omega}{c}\kappa K^{\prime}_{\nu}(\kappa a) & -\frac{k_z \nu}{a\gamma^2 \mu_1} J_{\nu}(\gamma a) & - \frac{\nu k_z}{\mu_2a\kappa^2}K_{\nu}(\kappa a) \end{array} \right) \left( \begin{array}{c} A_e\\ B_e\\ A_b\\ B_b \end{array} \right) = 0,$



8. Дисперсионное соотношение


Для существования нетривиального решения системы линейных уравнений, определитель матрицы должен равняться нулю:

$\left( \frac{\varepsilon_1\mu_1}{x^2}+\frac{\varepsilon_2\mu_2}{y^2}\right) \left( \frac{1}{x^2} + \frac{1}{y^2}\right)\nu^2 = \left[ \mu_2 g(y)+\mu_1 f(x)\right] \left[ \varepsilon_2g(y) + \varepsilon_1 f(x)\right] .$

В этой записи нулевого детерминанта использованы обозначения: $f(x) = \frac{J^{\prime}_{\nu}(x)}{xJ_{\nu}(x)}, \, g(y) = \frac{K^{\prime}_{\nu}(y)}{yK_{\nu}(y)},$ $x=\gamma a,\,y=\kappa a$ и соотношения: $\frac{\omega^2}{c^2} = \frac{\kappa^2+\gamma^2}{\varepsilon_1\mu_1 - \varepsilon_2\mu_2},\,k_z^2 = \frac{\varepsilon_1\mu_1\kappa^2+\varepsilon_2\mu_2\gamma^2}{\varepsilon_1\mu_1 - \varepsilon_2\mu_2}$, которые следуют из введенных ранее определений: $\gamma^2 = \frac{\varepsilon_1\mu_1}{c^2}\omega^2 - k_z^2, \, \kappa^2 = k_z^2 - \frac{\varepsilon_2\mu_2}{c^2}\omega^2$.

Величины $x,\,y$ — связаны еще одним равенством, следующим из двух последних определений и утверждения, что $k_z$ — едина для всех компонент:

$x^2+y^2 = (\varepsilon_1\mu_1 - \varepsilon_2\mu_2)a^2\frac{\omega^2}{c^2}.$



9. Моды


Для нахождения $x,\,y$ из системы уравнений:

$\left( \frac{\varepsilon_1\mu_1}{x^2}+\frac{\varepsilon_2\mu_2}{y^2}\right) \left( \frac{1}{x^2} + \frac{1}{y^2}\right)\nu^2 = \left[ \mu_2 g(y)+\mu_1 f(x)\right] \left[ \varepsilon_2g(y) + \varepsilon_1 f(x)\right],$

$x^2+y^2 = (\varepsilon_1\mu_1 - \varepsilon_2\mu_2)a^2\frac{\omega^2}{c^2},$

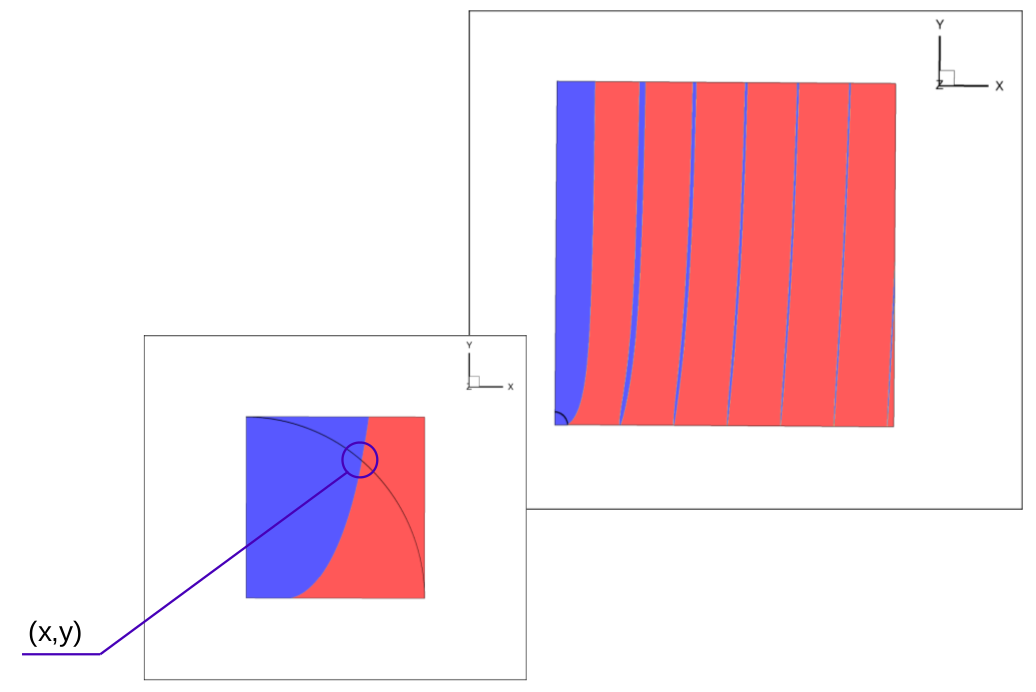
необходимо задать: $\nu,\,\omega,\,\varepsilon_1,\,\mu_1,\,\varepsilon_2,\,\mu_2,\,a$.

Связь $x$ и $y$ первым уравнением представляет собой серию линий на плоскости (граница раздела между синим и красным цветами, см. рис. ниже). Характер линий зависит от $\nu$.

Связь $x$ и $y$ вторым уравнением представляет собой окружность с радиусом, линейно зависящим от $a$. Точки пересечения линий являются решениями системы уравнений.



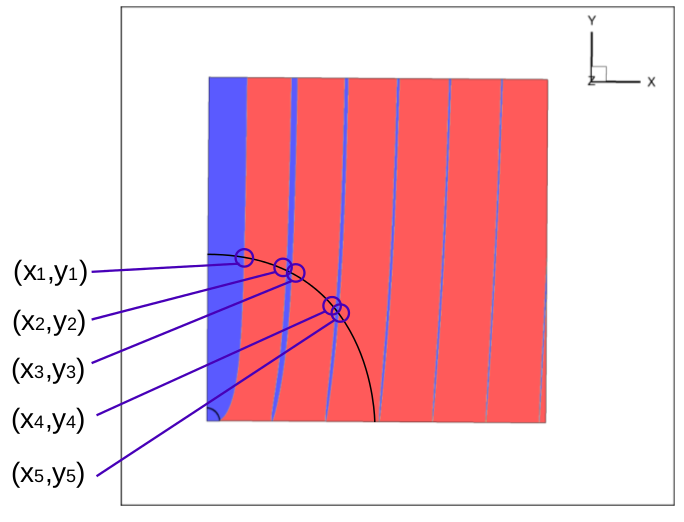
Набор решений составляет конечное число пар чисел $(x_i,y_i)$. Каждой такой паре чисел соответствует конфигурация электромагнитного поля, называемой «собственной модой».

Моду оптоволокна принято обозначать следующим образом: две буквы ($E,\,H$) — на первом месте буква с наибольшей $z$-компонентой и два индекса: на первом месте $\nu$, на втором номер ветви (на рисунке обозначена синим цветом).

Примеры обозначения:

$HE_{11}$ говорит о том, что $H_z$ больше, чем $E_z$, $\nu=1$, выбрана пара (см.рис. выше) $(x_1,y_1)$,
$EH_{13}$ говорит о том, что $E_z$ больше, чем $H_z$, $\nu=1$, выбрана пара (см.рис. выше) $(x_5,y_5)$ (третья синяя ветвь).

10. Порядок построения компонент поля


Подготовительные вычисления:

01. Задать $\nu,\,\omega,\,\varepsilon_1,\,\mu_1,\,\varepsilon_2,\,\mu_2,\,a$;
02. Найти наборы $(x,y)$, выбрать один, (п.9);
03. Вычислить $k_z,\,\gamma,\,\kappa$, (п.8);
04. Вычислить $A_e,\,A_b,\,B_e,\,B_b$, (п.7).

Выражения в цилиндрических координатах компонент поля:

$e_z = A_eJ_{\nu}(\gamma r)\exp\left\lbrace i\nu \varphi \right\rbrace,\text{ при }r<a, $

$e_z = B_eK_{\nu}(\kappa r)\exp\left\lbrace i\nu \varphi \right\rbrace,\text{ при }r>a, $

$b_z = A_bJ_{\nu}(\gamma r)\exp\left\lbrace i\nu \varphi \right\rbrace,\text{ при }r<a, $

$b_z = B_bK_{\nu}(\kappa r)\exp\left\lbrace i\nu \varphi \right\rbrace,\text{ при }r>a. $

Далее, при $r < a$:

$\left( \begin{array}{c} b_r\\ b_{\varphi} \end{array} \right) = \frac{i}{\gamma^2}\left\lbrace k_z \left( \begin{array}{c} A_b \gamma J^{\prime}_{\nu}(\gamma r) \\ \frac{1}{r} i \nu A_b J_{\nu}(\gamma r) \end{array} \right) + \varepsilon\mu\frac{\omega}{c} \left( \begin{array}{c} -\frac{1}{r} i\nu A_e J_{\nu}(\gamma r)\\ A_e \gamma J^{\prime}_{\nu}(\gamma r) \end{array} \right) \right\rbrace \exp(i\nu \varphi) ,$

$\left( \begin{array}{c} e_r\\ e_{\varphi} \end{array} \right) = \frac{i}{\gamma^2}\left\lbrace k_z \left( \begin{array}{c} A_e \gamma J^{\prime}_{\nu}(\gamma r)\\ \frac{1}{r} i\nu A_e J_{\nu}(\gamma r) \end{array} \right) - \frac{\omega}{c} \left( \begin{array}{c} -\frac{1}{r}A_b i\nu J_{\nu}(\gamma r)\\ A_b \gamma J^{\prime}_{\nu}(\gamma r) \end{array} \right) \right\rbrace \exp(i\nu \varphi).$

При $r > a$:

$\left( \begin{array}{c} b_r\\ b_{\varphi} \end{array} \right) = -\frac{i}{\kappa^2}\left\lbrace k_z \left( \begin{array}{c} B_b \kappa K^{\prime}_{\nu}(\kappa r) \\ \frac{1}{r} i \nu B_b K_{\nu}(\kappa r) \end{array} \right) + \varepsilon\mu\frac{\omega}{c} \left( \begin{array}{c} -\frac{1}{r} i\nu B_e K_{\nu}(\kappa r)\\ B_e \kappa K^{\prime}_{\nu}(\kappa r) \end{array} \right) \right\rbrace \exp(i\nu \varphi) ,$

$\left( \begin{array}{c} e_r\\ e_{\varphi} \end{array} \right) = -\frac{i}{\kappa^2}\left\lbrace k_z \left( \begin{array}{c} B_e \kappa K^{\prime}_{\nu}(\kappa r)\\ \frac{1}{r} i\nu B_e K_{\nu}(\kappa r) \end{array} \right) - \frac{\omega}{c} \left( \begin{array}{c} -\frac{1}{r}B_b i\nu K_{\nu}(\kappa r)\\ B_b \kappa K^{\prime}_{\nu}(\kappa r) \end{array} \right) \right\rbrace \exp(i\nu \varphi).$

Далее

$\textbf{E}(x,y,z,t) = \left( \begin{array}{c} e_r(x,y)\\ e_{\varphi}(x,y)\\ e_z(x,y) \end{array} \right) \exp\left\lbrace ik_zz - i\omega t \right\rbrace, \quad \textbf{B}(x,y,z,t) = \left( \begin{array}{c} b_r(x,y)\\ b_{\varphi}(x,y)\\ b_z(x,y) \end{array} \right) \exp\left\lbrace ik_zz - i\omega t \right\rbrace.$

При этом замыкающие соотношения стандартные:$\textbf{D}=\varepsilon_{1,2} \textbf{E},\, \textbf{B}= \mu_{1,2} \textbf{H}$(индексы указывают на соответствующие среды).

Выражение поля в декартовой системе координат через цилиндрические для электрических компонент:

$\left( \begin{array}{c} E_x\\ E_y\\ E_z \end{array} \right) = \left( \begin{array}{ccc} \cos\varphi & -\sin\varphi & 0\\ \sin\varphi & \cos\varphi & 0\\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} E_r\\ E_{\varphi}\\ E_z \end{array} \right).$

Для магнитных компонент матрица та же.

11. Замечания


Выбирая $a$ можно добиться единственности решения:

Такое оптоволокно называется одномодовым. Однако следует заметить, что «одномодовость» зависит от частоты — более высокие частоты распространяются в «одномодовом» волокне в виде набора мод.

Векторы компонент поля моды $HE_{11}$ в плоскости практически соправлены. Общая картина вращается во времени (см. видео ниже).


Для интереса ниже показана эволюция в течении временного периода моды $HE_{11}$


и моды $HE_{31}$
Поделиться с друзьями
-->

Комментарии (35)


  1. kentaskis
    12.04.2017 08:39
    #10000678

    Вам что-нибудь говорит фамилия Крафтштудт?)


    1. FransuaMaryDelone
      12.04.2017 09:03
      #10000714

      Погуглил сейчас… Это персонаж из литературного произведения? Или Вы другого Крафтштудта имели в виду?


      1. kentaskis
        12.04.2017 09:06
        #10000718
        +1

        Да, «Уравнения Максвелла» А. Днепрова


        1. FransuaMaryDelone
          12.04.2017 09:38
          #10000826

          Спасибо, почитаю)


  1. alexandrspiridonov
    12.04.2017 10:48
    #10001030

    Молодец) вот тебе книга если хочешь считать не только круглые волноводы
    http://shelly.kpfu.ru/e-ksu/docs/F136293242/Dautov_Karchevskiy_book_2009.pdf


    1. FransuaMaryDelone
      12.04.2017 11:05
      #10001082

      Вот как раз пример, где снова написано вскользь. Эти книжки, похоже, все такие.


      1. kbtsiberkin
        12.04.2017 11:51
        #10001224

        Тонкие математические детали, по-видимому, описываются в рамках разного рода «Уравнений математической физики». Поприкалываться над хвостистами, что ли…


        1. FransuaMaryDelone
          12.04.2017 12:03
          #10001282

          А кто такие «хвостисты»?


          1. kbtsiberkin
            12.04.2017 12:08
            #10001294
            +2

            Конкретно тут — студенты-физики, не сдавшие методы математической физики. Хотя в этом году уже все сдали, но следующий год впереди.


            1. FransuaMaryDelone
              12.04.2017 12:26
              #10001356

              Поприкалываться над хвостистами, что ли…
              Это Вы им такую вот (как в статье) задачу дать хотите?! А как же Христос?


              1. kbtsiberkin
                12.04.2017 12:31
                #10001360

                Ранее в стандартном годовом курсе электродинамики простейшие волноводы всегда считали. Сейчас вот остался от него один семестр, и то без электродинамики сплошных сред. По методам матфизики 14 лекций и 14 практик (из которых две контрольных). Связь уравнений с реальностью теряется у студентов, нехорошо.


                1. FransuaMaryDelone
                  12.04.2017 13:19
                  #10001510

                  Да, нехорошо. Ну если сдюжат за пару, то респект им.


  1. kazych
    12.04.2017 10:48
    #10001032

    А как вычислить константы A и B в пункте 7, если там матрица вырождена?


    1. FransuaMaryDelone
      12.04.2017 11:07
      #10001090

      ну… есть широко известный способ.


    1. alexandrspiridonov
      12.04.2017 13:10
      #10001478

      Легко, фиксируешь одно значение A_e=1, остальные уже вычисляешь)


      1. FransuaMaryDelone
        12.04.2017 13:13
        #10001488

        Уоу! Так можно сильно ошибиться.


        1. alexandrspiridonov
          12.04.2017 13:29
          #10001532

          В пункте 7 ты получил СЛАУ, для простоты напишу A(\kappa,\gamma)x=0. Фиксируешь \nu (номер решения) -он ещё называется азимутальный индекс. Находишь корни (\kappa,\gamma) функции f(\kappa,\gamma)=abs(det(A(\kappa,\gamma)). Теперь для этих значений у тебя имеется матрица A. Фиксируешь A_e=1, находишь все остальные константы.


          1. alexandrspiridonov
            12.04.2017 13:36
            #10001578

            ps. На практике вместо нахождения корней (\kappa,\gamma) функции f, лучше находить min_{\kappa,\gamma) 1/cond(A(\kappa,\gamma)), где cond- число обусловленности матрицы.


          1. FransuaMaryDelone
            12.04.2017 14:30
            #10001720

            в конкретно этой задаче, предлагаю Вам рассмотреть случай и убедиться, что существует решение с Другими словами, Вы ошибаетесь.


            1. alexandrspiridonov
              12.04.2017 15:55
              #10002026

              Ну тогда если Ae=0, значит e{z}=0, при r<a. Следовательно электрическая составляющая поля вдоль оси z нуль. А я всегда думал, что разыскивают ненулевые решения)


              1. alexandrspiridonov
                12.04.2017 16:19
                #10002142

                Из за условия сопряжения следует что и e_z=0 при r=a, а следовательно и везде Е=0


  1. nikolay_karelin
    12.04.2017 15:39
    #10001964

    Насколько я знаю, самый полный анализ собственных мод будет в книге Снайдера и Лава "Теория оптических волоноводов", скорее всего, там все формулы будут. Правда через нее продраться еще тот квест, тяжело написана.


    Кстати, такое решение как у вас (векторные моды) используется не очень часто, люди больше пользуются приближенными LP-модами. И еще одна проблема с (полу-)аналитическим решением — его можно записать, насколько я знаю, только для двух типов волокон — такого как у вас (step-index) и с бесконечным параболическим профилем (graded-index). И все равно надо численно считать постоянную распространения.


    А сейчас очень популярными стали волокна с параболическим профилем сердцевины и дополнительным провалом показателя преломления вокруг нее (trench-assisted fiber), с ними гораздо проще численно работать.


    1. FransuaMaryDelone
      12.04.2017 16:36
      #10002212

      спасибо, почитаю.


  1. Duduka
    12.04.2017 16:20
    #10002150

    А почему не в потенциалах (тех или других)? тем более в среде без проводников.


    1. FransuaMaryDelone
      12.04.2017 16:32
      #10002202

      А нужды нет. Как бы «зачем вводить сущности».


      1. Duduka
        12.04.2017 16:39
        #10002234

        Чтобы вместо 6D+1 оперировать в 4D+1.


        1. FransuaMaryDelone
          12.04.2017 16:44
          #10002254

          Но оперирование же происходит двумя z-компонентами.


          1. Duduka
            12.04.2017 17:07
            #10002354

            У Вас за все отвечает векторный потенциал, это 3D, B и E выражаются через него, они связаны в среде без проводимости, и Вы практически дублируете решение. e_z и b_z — результат «зачем вводить сущности»…


            1. FransuaMaryDelone
              12.04.2017 18:16
              #10002540

              Я уже ответил Вам выше. Дискутировать на тему потенциала не вижу смысла.


  1. aslepov78
    19.04.2017 04:21
    #10013180

    Какой смысл в этой статье? По решению уравнений Максвелла тонны хороших книг. А в наши дни еще и софт есть доступный.


    1. FransuaMaryDelone
      19.04.2017 04:29
      #10013182

      Мне казалось, что смысл предельно ясно выражен словами «аналитическое выражение электромагнитного поля» над катом. Чтоб «доступный софт» верифицировать, например.


      1. aslepov78
        19.04.2017 09:28
        #10013386

        Никольский В.В., Никольская Т.И. Электродинамика и распространение радиоволн
        Федоров Н.Н. — Основы электродинамики

        — открываем, читаем… меняем название на позвучнее, копипастим на хабр. Неплохой метод клепания статей.


        1. FransuaMaryDelone
          19.04.2017 15:29
          #10014442

          — открываем, читаем… меняем название на позвучнее, копипастим на хабр.
          Это неправда: откройте, почитайте и сравните со статьей — статья не является выдержкой из книжки.

          Спасибо за ссылку, книжка хорошая.


          1. aslepov78
            19.04.2017 15:44
            #10014482

            Книжки — классика.

            А зачем вообще вам это? Вы никак резонатор лазера взялись расчитать? Небось еще оптоволоконного. Аналитические методы в электродинамике — это песчинка в океане. Не лучше ли сразу численно моделировать то что вам надо? А в лазерах ведь надо прикрутить еще квантовую электродинамику как то.


            1. FransuaMaryDelone
              19.04.2017 16:22
              #10014568

              работа у меня такая.