Приращения
Начнем, пожалуй, с любимых нами векторов. Свойство векторов — их можно рисовать в любой точке пространства, пользуясь параллельным переносом — это свойство может показаться удивительным. Как так?! Зачем это? И главное — с этим связаны разные смешные вопросы-упражнения.
Например: нарисуйте в двумерной декартовой системе координат вектор, который начинается в точке (0,1) и имеет координаты (1,0). У меня в группе не все студенты могли это сделать (спасибо школе). Второй курс, между прочим. Они еще физиками себя называли гордо. Всякую ерунду рисовали… вроде такого:
Поэтому все-таки сделаем это один раз. Нарисуем.
Опишем этот «сложный» алгоритм:
1. Отмечаем точку, которая называется «координаты вектора»;
2. рисуем вектор: проводим стрелку из «нуля» в точку, которая называется «координаты вектора»;
3. рисуем точку, которая называется «в ней начинается вектор» — это будет «новый ноль» для нашего ориентированного отрезка (вектора);
4. переносим наш вектор на новое начало и сажаем, чтоб там рос (параллельный перенос — называется).
Мораль:
а) Начинаться вектор может из любой точки пространства. Всё равно это один и тот же вектор. Это один и тот же объект. У вектора только две характеристики — это направление и величина. Всё! Никакого начала и никакого конца! Математика не различает эти штуки: начала и концы. Если величина и направления совпадают, то всё! хватит! — это один вектор. Откуда он начинается и где заканчивается — это для формальной математики неважно. Ну если Вам сильно не нравится, что нарисовано два вектора, а я заставляю говорить, что он один, то думайте про себя так: «это два равных, абсолютно одинаковых вектора». А если Вам кажется, что они все-таки как-будто немножко разные, ну начинаются в разных местах же! Это же волнует, я Вас понимаю — есть же разница откуда расти вектору; мы же видим: если гвоздь из середины дороги торчит — это не то же самое, как на обочине в кустах торчал бы! Да, я Вас успокою — это нормально, разница есть. Для того, чтоб такую разницу учесть, люди придумали новый объект — векторное поле. Целое поле, представляете?! Из векторов! Поговорим еще про него потом.
б) И еще: мы не будем говорить слово «длина вектора» — это некрасивое слово. Оно некрасивое потому, что у «длин» векторов бывают разные размерности. Например вектор силы имеет величину, измеряемую в ньютонах, а величина вектора перемещения измеряется в метрах. Чтоб помнить о разных величинах разных векторов, будем себя всегда одергивать. Никогда не произносите вслух мантру: «длина вектора» — а то язык отвалится (про себя думать можно про длину, но недолго). Правильно говорить: «ВЕЛИЧИНА вектора»… и благоговеть слегка при этом.
в) Итак… Когда произносят слова «координаты вектора», это значит, что его начали рисовать из нуля. Это нам потом еще пригодится, когда будем векторное поле засеивать. А сейчас нам этот параллельный перенос пригодится, чтобы про приращения поговорить.
Давайте посмотрим на рисунок:
Тааак… Какой-то синий вектор, какой-то красный. Называются одинаково… И между ними натянута двойная стрелка…
называется — она не вектор — у нее нет начала, только два конца. Вообще мы тут про «приращения» собрались говорить. Поэтому пару слов про то, что у нас прирастать будет. Математике все равно, что у нас прирастает. Можно было бы имена разные дать нашим векторам, потом вычесть какой-нибудь один из другого и успокоиться. Но мы будем называть оба вектора одной буквой, а отличать их будем цветом. И говорить будем про приращение «этого вектора». Представим, что этот вектор как-то меняется, он для нас что-то значит. Например это вектор описывает скорость автомобиля или силу трения… Ну в общем что-то он означает такое, что остается за кадром, но оно есть — процесс какой-то, двигается кто-то или деньги тратит, а может нагревается — что-то происходит в общем, а вектор 
описывает это происходящее. А иначе эти всякие приращения вообще не нужны и бессмысленны. В общем, хочется обратить Ваше внимание на одну тонкость, а именно — на закон упорядочивания.Если мы нарисуем стрелку отрезку
(вот так вот: 
), то можно смело назвать то, что получится (а получится у нас «дельта эр со стрелкой»): — приращением вектора . Надо только сообразить «в какую сторону растет» вектор . Надо как-то пронумеровать что ли их: синего и красного. Кто-то должен взять на себя смелость и «задать закон», т.е. сказать, какой вектор начальный, а какой конечный. Ну давайте я пронумерую. Вот так уже лучше: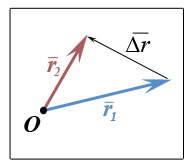
Да, мне показалось, что синий
— это вектор начальный, а красный 
— конечный. Идея понятна? — Нам нужна какая-то причина, чтобы упорядочить векторы, чтоб сказать, какой будет первым, а какой вторым. Обычно это какая-нибудь естественная причина, например «время»: сначала был один вектор, а потом другой. Или не «время»… а «пространство»: координата маленькая — значит начало, а координата побольше — значит конец. Но какое-то соображение, какой-то закон нумерации векторов всегда нужен. Да он и есть всегда, только не всегда озвучивается. Вот тут люди и ошибаются с минусом, в этом месте — забывают следить за законом, который упорядочивает… Ну а дальше, как только такой закон имеется, то приращение чего-нибудь (например вектора, а может какого-нибудь скаляра или, прости Господи, тензора...) сразу автоматом вычисляется по одному единому монументальному правилу: «КОНЕЦ МИНУС НАЧАЛО» — и это не переломить. Обязательно из «конца» вычитается «начало». Во всех случаях, всегда, вечно, во всех алгоритмах. Это важно помнить, чтоб не ошибаться: сначала закон упорядочивания, потом «конец минус начало». Вон посмотрите на рисунок еще раз: из второго вектора вычли первый — первый показывает начало, откуда растет «приращение вектора», а втыкается «приращение» в стрелочку второго вектора — всё, конец тут у вектора приращения. Потому что приращение — это «КОНЕЦ МИНУС НАЧАЛО». Заметим между делом, что если бы не параллельный перенос и не вот это вот «пренебрежение» к началу и концу вектора, то мы бы такого красивого треугольничка не нарисовали. Пришлось бы всё рисовать из нуля. Ёжика ершистого. Вот так вот:
Это тоже правильно, но меньше наглядно.
— А где базисные векторы?! Почему только ноль нарисован? — спросите вы.
Ну… о системах координат мы чуть позже поговорим. А тут их не рисуем, чтоб подчеркнуть, что это неважно — не зависит от системы координат сложение векторов — мы так захотели, мы это придумали! Нам нравится, чтоб не зависело сложение векторов от системы координат и нет на нас управы! Тут мы — боги! Кстати, радоваться рано, мы потом поплатимся за эту свою божественность, каждая наша «хотелка» влечет ответственность — это математика же, а не фэнтези какое-нибудь.
— Но, позвольте! — скажете Вы. — Какое сложение векторов?! Где?! Вроде мы из второго вектора вычитали первый вектор. Вычитали, а не складывали!
Да, вычитали. А называем сложением, да. Вот так вот. Мы «складывали». Просто один вектор еще и умножили на «минус один» и коварно ничего не сказали об этом. Ну давайте скажем: Сложение и вычитание формально ничем не отличаются, потому что вектор "
" точно такой же полноценный вектор, как и "" — у них даже величина совпадает, просто они смотрят в разные стороны. И все математические формальные алгоритмы ко всем векторам одинаково хорошо относятся, поэтому эти две операции называют одним словом «сложение» — это для краткости.Системы координат
Один человек, имея в кармане 100 денюшек, пошел на базар. Походил-посмотрел… в одном углу базара увидел арбузы по 2 денюшки за штуку, а в другом углу арбузы были подороже — 3 денюшки за штуку. Ура! Можно нажиться на спекуляции! Купить подешевле, продать подороже! На все деньги! И так четыре раза!
Давайте нарисуем на графике, как он четыре раза это всё делал. Отметим точками на координатной плоскости этот процесс из четырех шагов. Точки соединим стрелками… Арбузы отложим по вертикали, а денюшки — по горизонтали. Да еще, чтоб посмешнее было, похулиганим: рост в обратную сторону пустим, не так как у всех (инверсия системы координат у нас получится). Сначала человек находился в нулевом пункте: 100 денюшек и 0 арбузов, Это его точка «ноль»: (100,0). Потом он купил арбузы по 2 денюшки за штуку на все деньги! попал в точку «один»: (0,50), дальше продал арбузы с выгодой: (150,0) и так четыре раза. Смотрите, какая красота получается на графике:
Как вы думаете, вон те стрелочки, которые кружочки соединяют — это векторы?
конец четвертого урока. Продолжение следует.
Комментарии (33)
koldyr
17.04.2017 16:53+1И как теперь развидеть всё это?
Я понимаю, что школа, но почему нельзя в школе применять аксиматический подход — не понимаю. Ничего сложного в векторном пространстве над полем и в абелевой группе на уровне определений нет. И все проблемы отпадают сами собой
GeMir
17.04.2017 18:09Хотя бы потому, что школа — это ограниченное количество часов и гетерогенные классы. Это хорошо, что у вас не вызывают проблем векторные пространства и группы.
bfDeveloper
17.04.2017 19:43-1На первом курсе можно было разделить студентов на 3 группы. Говоришь фразу «Вектор и точка — одно и то же», и следишь за реакцией. Те кто спокойно соглашаются, явно на своём месте в математике. Они хорошо сдадут сессию. Те, кто согласен с сутью, но имеет семантические дополнения и спорят о верности высказывания, тоже далеко пойдут. Эти люди кроме равенства понятий видят ещё и коммуникационную проблему терминологии и «школьные» проблемы восприятия, что вектор — стрелка, а точка — точка. Они их видят и решают, понимая абстракцию. Ну и «безнадёжная» третья категория, доказывающая, что это принципиально!!11 разные вещи. Они не спорят об интерпретации, у них просто нет абстрактного мышления. Третья группа не поймёт потом и вектор в пространстве интегрируемых функций, не сможет перенести неравенство треугольника в функциональное пространство и обобщить, потому что это абстракция, а не стрелочка на бумаге.
Это всё к чему? А к тому, что пост очень поощряет третью категорию, запутывая потенциальных математиков из первых двух. Радиус-вектор, имхо, школьная попытка использовать абстракцию, не объясняя её.
Andy_U
18.04.2017 08:23Не всегда. При переходе в новую систему координат (сдвигом начала координат) все три координаты точки в общем случае меняются, а проекции вектора (скорости) на оси — нет. А при переходе в движущуюся систему отсчета (начало координат которой в данный момент времени совпадает со старой), то координаты точки (в тот же момент времени) совпадут, а вот вектора скорости будут разными.
koldyr
18.04.2017 13:18+1Всё смешалось. Физика с математикой. Афинные пространства с векторными. Абстракции с интерпритациями.
Andy_U
18.04.2017 14:22Ну, положим, я писал конкретно про физику. И если вы считаете, что вектор скорости в Ньютоновской механике, это не вектор с точки зрения математика, то я бы очень хотел бы объяснений. Просьба к двухтомнику Лорана Шварца не отсылать — много лет назад пришлось вернуть хозяину :(
koldyr
18.04.2017 15:20+1К сожалению двухтомником тут не обойтись.
Есть такая байка. Однажды к Гильберту пришли физики и спросили про что-то матрица оно или оператор. Гильберт ответил что в данном случае это одно и тоже. Физики не поняли и обиделись.
Так как вы описали — скорость можно рассматривать как элемент афинного пространства. Тогда переходы между инерциальными системами отсчета будут гомоморфизмами афинных пространств. Но не будут гомоморфизмами векторных пространств, так как гомоморфизмы векторных пространств оставляют 0 на месте.
Andy_U
18.04.2017 17:03Хмм, а давайте забудем про движущиеся относительно друг друга системы отсчета и посмотрим на определение афинного пространства в википедии:
Аффинное пространство
Аффи?нное простра?нство — математический объект (пространство), обобщающий некоторые свойства евклидовой геометрии. В отличие от векторного пространства, аффинное пространство оперирует с объектами не одного, а двух типов: «векторами» и «точками».
Все равно — три компоненты, значит, вектор?koldyr
18.04.2017 17:22А если одна компонента, это вектор? А если 101? О чём вообще этот вопрос. Есть строгие аксиоматические определения. Дочитайте статью в Вики до конца.
Andy_U
18.04.2017 17:41Мы, возможно, перестали понимать друг друга. Я своим первым сообщением попытался опровергнуть утверждение bfDeveloper что «Вектор и точка — одно и то же», Вы мое сообщение раскритиковали. Ну, возможно, я и в самом деле зря полез в физику, хотя что взять с бывшего физика-теоретика. В общем, Вы, пожалуйста, ответьте, Вы с мнением bfDeveloper согласны или нет?
koldyr
18.04.2017 18:20Все дело в различии подходов. Что такое вектор? Вектор это элемент векторного пространства над полем. Что такое векторное пространство? Это такое множество. Элементы этого с некотрой операцией + образуют абелеву группу. кроме этого есть отображение пары (вектор, элемент поля) в вектор. оно должно обладать некоторыми свойствами. ассоциативностью, скалярной и векторной дистрибутивностью, унитарностью.
Дальше из этого извлекается базис. И в случае конечномерности базиса теорема об изоморфизмах векторных пространств. Любое конечномерное векторное пространство изоморфно арифметическому пространству соответствующей размерности.
Вот таким образом и получается, что выбрав на плоскости особую точку 0 путем нехитрых операций можно превратить эту плоскость в векторное пространство.
Можно вводить стрелочки. Потом разбираться с кноцом, началом, длинной и паралельным переносом, с последующей факторизацией. Будет опять векторное пространство. Если они одной размерности над одним полем то они изоморфны. Как-то так.Andy_U
18.04.2017 18:51А Вы вот тут не ошиблись? Или «перевернули» термины?
кроме этого есть отображение пары (вектор, элемент поля) в вектор
Просто я смотрю в Википедию и вижу, что для афинных пространств определена операция сложения точки и вектора, в результате которой получатся точка (а не вектор). См.аксиому N3. Ну и сами вектора можно складывать. А разумной операции «сложения» точек — может и не быть. Как ее нет в реальном физическом пространстве. Вот и получается, что если мы одновременно работаем и с точками и с векторами, то мы должны их различать по типу. Собственно об этом и статья.koldyr
18.04.2017 19:00Да, тут вы правы операции сложения точек в афинном пространстве нет. Но вы можете рассматривать точки афинного пространства как скорости чего-то в какой-то системе отсчета. И рассматривать ассоциированные с ним элементы векторного пространства как приращения этих скоростей. При этом приращения инвариантны относительно сдвигов. А смена системы отсчета это — гомоморфизм афинных пространств. Просто это может быть удобно. А потом можно увеличить размерность пространства на 1 и представить эти гомоморфизмы как подгруппу группы линейных операторов на пространстве большей размерности. И так далее.
Andy_U
18.04.2017 19:30Просто это может быть удобно.
Так я и не говорил, что никогда нельзя отождествлять «вектора» и «точки». Лишь, что не всегда.bfDeveloper
19.04.2017 18:04Я соглашусь, что в случае афинного пространства у нас действительно сущности разделены на вектора и точки, чтобы не путать их друг с другом. Это действительно та область, где нельзя просто так сказать, что это одно и то же. Убедили.
Однако, согласитесь, что это в этой конкретной абстракции. Когда вы оперируете физическими величинами, вам не важно это разделение, так как множество точек само по себе является линейным пространством. Точно так же различия стираются во всех применениях над большинством пространств. То есть точка и вектор отличаются терминологически в рамках теории афинных пространств, но не отличаются в применениях.
Считайте этот аргумент «последней придиркой». В целом ваша аргументация принята.
bfDeveloper
18.04.2017 16:08А давайте более конкретный пример. Возьмём в качестве пространства — состояние твёрдого тела в задаче механики. У нас есть 6 пространственных координат (например центр и 3 угла) и 6 скоростей (пусть скорость центра и 3 угловых скорости). Решение какой-нибудь задачи управления будет производится на этом пространстве, например сажаем ракету на баржу. А теперь две формулировки: возьмём некую точку этого пространства, возьмём некоторый вектор в данном пространстве. Я утверждаю, что это абсолютно одно и то же. И то и другое — 12 вещественных чисел, двенадцатиимерный вектор. Язык не поворачивается сказать двенадцатимерная точка. Однако в той же задаче буде точка на фазовом портрете. То же пространство, те же 12 измерений, но слово «точка».
Когда у нас есть прямая геометрическая интерпретация, ещё есть смысл отличать вектор и точку. Но это только в малом количестве геометрических задач, а в большинстве даже физических задач эта интерпретация исчезает. Мы начинаем векторно перемножать координаты (точки в интерпретации), помещаем объекты по координатам вектора и много другое. Например мы можем умножить векторно относительные координаты объектов, чтобы понять, кто правее, а кто левее. Когда речь идёт о множестве подвижных систем координат напрочь исчезают различия векторов и точек.Andy_U
18.04.2017 16:23Если берем углы (поворота), то теряем коммутативность сложения. Т.е., результат поворота на угол А, скажем, вокруг оси X, а потом на B вокруг Y, это не тоже самое что сначала поворот на B вокруг Y, а потом на A вокруг X.
bfDeveloper
19.04.2017 17:55Хм, ну и что? Как это мешает быть вектором некоммутативной величине? Вектор по одному из определений — упорядоченное множество. Есть ещё масса так или иначе эквавалентных. Вектора превосходно существуют в любом пространстве, будь оно линейным, афинным или пространством розовых слонов. Коммутативность — свойство линейного пространства, но заметьте, сначала мы вводим понятие вектора, операций над ним, а потом уже коммутативность и пространство.
Andy_U
19.04.2017 18:10Вот тут дано определение векторного пространства, где написано, что операция сложения векторов должна быть коммутативна.
bfDeveloper
20.04.2017 17:51Я не спорю, но вектора существуют и вне векторного пространства. Чтобы множество векторов было векторным пространством нужна коммутативность и много чего ещё, это так. Но для определения самой сущности «вектор» этого не требуется.
Andy_U
20.04.2017 18:57Тогда, пожалуйста, всегда, когда Вы говоротите о таких «векторах», называйте их «векторами вне векторного пространства», чтобы никого не путать. Потому что общепринято называть такие объекты точками в многомерном пространстве, на многообразии и т.д. и т.п, а векторами объекты, которые можно складывать. Нет сложения с требуемыми свойствами — для математиков никакой это не вектор.
bfDeveloper
21.04.2017 00:49Наши рассуждения уже зашли далеко в терминологическую область. Перечитал вики ещё несколько раз и наконец-то понял в чём проблема и почему я вас не понимаю. Определений вектора много, мне привычно то, что называется кортеж. А слово кортеж за 6 лет на ВМК (Лобачевский, Нижний Новгород) я слышал буквально пару раз и в других контекстах. Чтож буду знать, что это ещё одно место где общепринятая терминология отличается от той, которой меня учили. Ну или которую я понял, не буду всё валить на других.
Не первый раз надо сказать уже натыкаюсь. У нас аналитическая и регулярная функция на ТФКП (комплексные функции) вообще не так как у всех вводились и то, что обычно понимают под регулярной у нас было аналитической. Что понимали под регулярной уже не помню. Сильно мешало, когда я пытался пользоваться чем-то кроме конспектов.
Буду привыкать к слову кортеж, раз именно его имею в виду.
koldyr
19.04.2017 19:35Мы тут с коллегой сошлись на том, что вектор это точка в векторном пространстве.
FransuaMaryDelone
19.04.2017 23:16Господа, прошу обратить внимание на частное мнение, что определения подчиняются цели исследователя — определения гибки и обязаны служить людям, а не наоборот.
Andy_U
20.04.2017 19:05Но если автор вместо общепринятых обозначений использует свои, или еще хуже, общепринятые обозначения из «другой оперы», то возникает подозрение, что цель автора — запутать читателей. Попробуйте отправить статью с подобной терминологией в научный журнал и и рецензент ее вернет по данным формальным причинам, не разбираясь в сути работы.
FransuaMaryDelone
21.04.2017 15:34Но если автор вместо общепринятых обозначений использует свои, или еще хуже, общепринятые обозначения из «другой оперы», то возникает подозрение, что цель автора — запутать читателей.
Ну ткните меня носом: где я ввел неправильное определение вектора или придумал про векторы «что-то особенное», чего Ваш любимый рецензент не пропустит. Кого я запутал?! что Вы несете?!Andy_U
21.04.2017 17:52Просто Вы приняли участие в дискуссии как раз про точность используемой терминологии, и мне показалось, что Вы не согласны с утверждением koldyr. Возможно, я Вас не понял, тогда поясните, пожалуйста, что Вы имели ввиду.
FransuaMaryDelone
21.04.2017 21:25Возможно, я Вас не понял, тогда поясните, пожалуйста, что Вы имели ввиду.
не вижу связи между Вашей способностью к пониманию и моей обязанностью пояснять. Всё, что я хотел сказать, я сказал. Но Вы вынуждаете меня сказать что-то еще. Извольте: «мы с коллегой сошлись» — это по-настоящему прекрасно, когда люди понимают друг друга. Но определения, кроме того, должны быть удобны — об этом некоторые иногда забывают в высоком стремлении формализовать всё вокруг. Я не вижу для себя удобства в определении вектора как «точка в векторном пространстве», — мне это ничего не дает, кроме вопроса «а что такое, тогда, векторное пространство? и что такое точка?». На этом я заканчиваю дискуссию.
GeMir
Вектор — это направление. Говоря о том, что «их можно рисовать в любой точке пространства» вы убеждаете учащегося в том, что вектор — это стрелка, которую мы рисуем. А это не так.
«Правильно говорить: „ВЕЛИЧИНА вектора“» — модуль вектора. Раз уж хочется правильно.
FransuaMaryDelone
а как Вы вводите векторное поле в криволинейной системе координат?
GeMir
Никак. У вас статья «по мотивам школьных уроков».
И ещё, мне кажется, было бы очень здорово, если бы вы избегали «сюсюкающего» («денюшки») и вымученно «захватывающего» («Целое поле, представляете?! Из векторов!», «еще, чтоб посмешнее было, похулиганим») стиля повествования.