04.05.2017 11:57
FransuaMaryDelone 31 2600 Источник
Есть стопка стеклянных пластинок и захотелось нам построить для этой стопки частотную характеристику пропускания (или отражения) света. Вот как на рисунке: берем две стеклянные пластинки (отличаются показателем преломления) — строим; потом собираем стопочку из 10 пластин (те же два показателя преломления чередуются) — опять строим; а в конце делаем стопочку потолще (из 50 пластин) — и снова строим. Интересная же картинка: для толстой стопки есть интервал частот, которые совсем не проходят, Т=0, — вот эта стопка называется "одномерный фотонный кристалл".
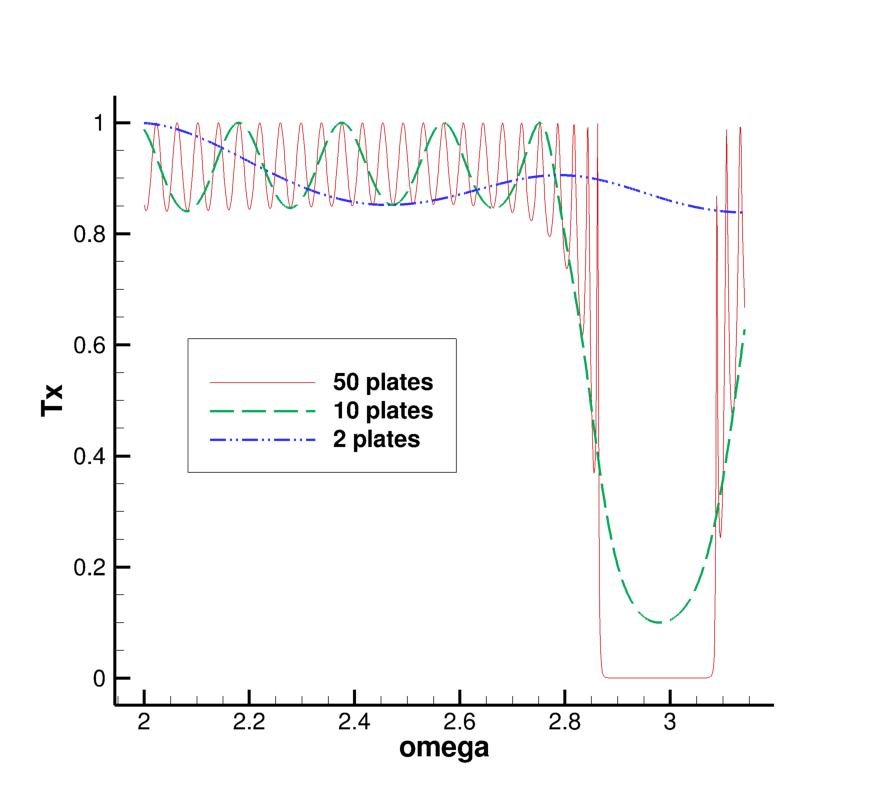
Ну а как строить-то такую характеристику? А если пластинки поглощающие? А вдруг они еще и анизотропные некоторые? А если не просто анизотропные, а прям холестерические, как в жидкокристаллических мониторах? А если все они вообще разные и каждая со своим дихроизмом? Не беда!

Статья ориентирована на тех, кто захочет написать код функции, поэтому без математических выкладок — всё в стиле «делай, не думай».

Постановка задачи

Отрезок $z \in [0,L]$ разделен на $n$ частей — «одномерных анизотропных пластин холестерического типа». Каждая пластина имеет свой собственный набор параметров: $\varepsilon_{\perp, i}$, $\varepsilon_{\parallel, i}$, $\mu_{\parallel, i}$, $\mu_{\perp, i}$, $q_i$, $\varphi_{0, i}$, а также толщину $d_i>0:\sum^{n}_{i=1}d_i=L$. Номера пластин упорядочены в порядке следования одной за другой слева направо (вдоль возрастания координаты $z$). Слева и справа от стопки анизотропных пластин находятся изотропные среды с параметрами: $\varepsilon_{0},\mu_{0}$ при $z<0$ и $\varepsilon_{L},\mu_{L}$ при $z>L$. Слева на стопку пластин падает плоская электромагнитная волна с частотой $\omega$. Требуется найти коэффициент отражения $R$ и коэффициент пропускания $T$.

Задача решается в безразмерных величинах. Параметр обезразмеривания $r^*_{sgs}$ выбирается исходя из удобства. Безразмерные величины выражаются через размерные в системе $SGS$ следующим образом:

$\vec{r}=\vec{r}_{sgs}/r^*_{sgs},\quad t=t_{sgs}\cdot c_{sgs}/r^*_{sgs},\quad\omega =\omega_{sgs}\cdot r^*_{sgs}/c_{sgs},\quad\sigma=\sigma_{sgs}\cdot 4\pi r^*_{sgs}/c_{sgs},\quad q=q_{sgs}\cdot r^*_{sgs}.$

При обезразмеривании вещественные части величин $\varepsilon,\, \mu$ не изменяются.


1. Предварительные слова


1.1. Аргументы и возвращаемые значения функции


Аргументы (уже обезразмеренные)

$\varepsilon_{0}$, $\mu_{0} $ — диэлектрическая и магнитная проницаемости крайней левой изотропной среды (не обязательно вакуум, индекс значит $z=0$),
$\varepsilon_{L}$, $\mu_{L} $ — диэлектрическая и магнитная проницаемости крайней правой изотропной среды (индекс: $z=L$),
$\omega $ — частота падающей волны,

Далее для каждого $i$-слоя (всего $n\in N$ слоев):

$d_i>0$ — толщина слоя,
$q_i$ — пространственная частота холестерической спирали (может принимать отрицательные значения),
$\varphi_{0, i}$ — «начальный» (какой он был бы при $z=0$, если спираль продолжить назад, — невзирая на истинную начальную координату $i$-слоя) угол между осью $O_x$ и вектором-директором $\textbf{n}$ (см рис. ниже),
$\varepsilon_{\perp, i}$, $\varepsilon_{\parallel, i}$, $\mu_{\parallel, i}$, $\mu_{\perp, i}\in C$ — в общем случае комплексные продольные и поперечные диэлектрические и магнитные проницаемости.

При этом мнимые части диэлектрических и магнитных проницаемостей отвечают за поглощение: $Im(\varepsilon_{\perp})=-{\sigma_{\perp}}/{\omega}$, $Im(\varepsilon_{\parallel})=-{\sigma_{\parallel}}/{\omega}$, $Im(\mu_{\perp})=-{\sigma^*_{\perp}}/{\omega}$, $Im(\mu_{\parallel})=-{\sigma^*_{\parallel}}/{\omega}$.


Возвращаемые значения

Всего рассматривается 4 типа падающих волн:

  • плоская поляризация по $x$,
  • плоская поляризация по $y$,
  • круговая поляризация правая $r$,
  • круговая поляризация левая $l$.

В соответствии с типом падающей волны, функция возвращает 4 коэффициента пропускания и 4 коэффициента отражения (всего 8 значений): $R_x, T_x, R_y, T_y, R_l, T_l, R_r, T_r$.

Коэффициенты определяются как доли энергии (отраженной, пропущенной) от энергии падающей волны.

При желании, долю поглощенной энергии $A$ в стопке можно вычислить по формуле: $A_{\alpha}=1-(R_{\alpha} + T_{\alpha})$, где индекс $\alpha$ обозначает тип падающей волны: $x,y,r,l$.

1.2. Используемые ниже обозначения


В основном действия состоят из вычисления и произведения комплексных матриц размерностью $4\times4$.

Для обозначения каждой матрицы используется открывающая скобка, буква и закрывающая скобка. Например:$[z),~(\beta\},~\{z\rangle$. Открывающая и закрывающая скобки не всегда одинаковы. Обратные матрицы обозначаются обратным порядком скобок, например: $\{z\rangle:=\langle z\}^{-1}$. Буквой $z$ в скобках подчеркивается зависимость марицы от координаты. Если матрица не зависит от координаты, то в скобках присутствует другая буква. Таким образом, при обозначении матрицы, значение имеет уникальный набор скобок и их порядок следования.

Обозначения используются для лаконичности записи произведения матриц и удобства проверки правильности записи, выражаемого мнемоническим правилом: соседние перемножаемые матрицы должны иметь одинаковые граничащие скобки, что имеет смысл при переходе из одного пространства в другое. Эти-то 4-мерные пространства и обозначаются скобками: $]$ — пространство «неподвижное декартово», $)$ — пространство «вращающееся декартово», $\}$ — пространство «собственных векторов», $\rangle$ — пространство «количеств и направлений волн». Произведение матрицы на вектор интерпретируется как новое представление вектора: или в другом 4-пространстве, но при той же координате (если скобки матрицы отличаются) или в другой координате, но в том же 4-пространстве (если открывающя и закрывающая скобки одинаковы).

2. Вычислительные шаги


2.1. Вычисление собственных значений $\lambda$


Для каждого слоя вычисляются 4 собственных значения по формуле:

$\lambda=\pm i \sqrt{\eta\pm\tau},$

где

$\eta = \frac{\omega^2}{2}(\varepsilon_{\perp}\mu_{\parallel}+\varepsilon_{\parallel}\mu_{\perp}) + q^2,$

$\tau = \sqrt{\frac{\omega^4}{4}(\varepsilon_{\perp}\mu_{\parallel}-\varepsilon_{\parallel}\mu_{\perp})^2 +\omega^2 q^2(\varepsilon_{\perp}\mu_{\parallel}+\varepsilon_{\parallel}\mu_{\perp} + \varepsilon_{\perp}\mu_{\perp}+\varepsilon_{\parallel}\mu_{\parallel})}.$

Здесь $i$ — мнимая единица.

2.2. Вычисление собственных векторов $\vec{\beta}$


Каждому собственному значению $\lambda$ соответствует собственный вектор $\vec{\beta}$: $(m)\vec{\beta}=\lambda\vec{\beta}$, где

$(m) := \left ( \begin{array}{cccc} 0 & q & 0 & -i\omega\mu_{\perp}\\ -q & 0 & i\omega\mu_{\parallel} & 0\\ 0 & i\omega\varepsilon_{\perp} & 0 & q\\ -i\omega\varepsilon_{\parallel} & 0 & -q & 0 \end{array} \right ).$


Если $\lambda$ кратности 2, то в этой задаче ему соответствует два собственных вектора.

2.3. Вычисление матрицы $[D_i]$


Для каждой $i$-слоя вычисляется матрица $[D_i]$. Нумерация слоев слева-направо, по возрастанию координаты $z$. Формула для вычисления:

$[D_i]=[z_l)(\beta\}\{M_i\}\{\beta)(z_r],$

где

$\{M_i\}= \left ( \begin{array}{cccc} \exp (-\lambda_{1,i} d_i) & 0 & 0 & 0\\ 0 & \exp (-\lambda_{2,i} d_i) & 0 & 0\\ 0 & 0 & \exp (-\lambda_{3,i} d_i) & 0\\ 0 & 0 & 0 & \exp (-\lambda_{4,i} d_i) \end{array} \right ),$

$(\beta\}:= \left ( \begin{array}{llll} \begin{array}{c} {\vdots}\\ \vec{\beta}_1\\ {\vdots} \end{array} & \begin{array}{c} {\vdots}\\ \vec{\beta}_2\\ {\vdots} \end{array} & \begin{array}{c} {\vdots}\\ \vec{\beta}_3\\ {\vdots} \end{array} & \begin{array}{c} {\vdots}\\ \vec{\beta}_4\\ {\vdots} \end{array} \end{array} \right ),$

$[z):= \left ( \begin{array}{cccc} \cos (qz+\varphi_0) & -\sin (qz+\varphi_0) & 0 & 0\\ \sin (qz+\varphi_0) & \cos (qz+\varphi_0) & 0 & 0\\ 0 & 0 & \cos (qz+\varphi_0) & -\sin (qz+\varphi_0)\\ 0 & 0 & \sin (qz+\varphi_0) & \cos (qz+\varphi_0) \end{array} \right ),$

$(z]:= [z)^{-1}$, $\{\beta):=(\beta\}^{-1}$, $z_l,z_r$ — координаты соответсвенно левой и правой границы $i$-слоя: $z_r-z_l=d_i$.

2.4. Вычисление матрицы $[D]$


Формула для вычисления:

$[D] = [D_1]\dots [D_{n-1}][D_n].$



2.5. Вычисление матрицы $\langle U\rangle $


Формула для вычисления:

$\langle U\rangle = \langle 0][D][L\rangle,$

где

$\begin{array}{c} \displaystyle [L\rangle = \left ( \begin{array}{cccc} e^{-i\omega\rho_L L} & 0 & e^{i\omega\rho_L L} & 0\\ 0 & e^{-i\omega\rho_L L} & 0 & e^{i\omega\rho_L L} \\ 0 & -e^{-i\omega\rho_L L}\cdot\rho_L/\mu_L & 0 & e^{i\omega\rho_L L}\cdot\rho_L/\mu_L \\ e^{-i\omega\rho_L L}\cdot\rho_L/\mu_L & 0 & -e^{i\omega\rho_L L}\cdot\rho_L/\mu_L & 0 \end{array} \right ),\\ \displaystyle \langle 0] = \frac{1}{2} \left ( \begin{array}{cccc} 1 & 0 & 0 & \mu_0/\rho_0 \\ 0 & 1 & -\mu_0/\rho_0 & 0\\ 1 & 0 & 0 & -\mu_0/\rho_0 \\ 0 & 1 & \mu_0/\rho_0 & 0 \end{array} \right ), \end{array} $

при $\rho_L = \sqrt{\varepsilon_L\mu_L}$, $\rho_0 = \sqrt{\varepsilon_0\mu_0}$.

2.6. Вычисление векторов $\textbf{c} $


Предварительные вычисления. Если

$\langle U\rangle = \left ( \begin{array}{cccc} u_{11} & u_{12} & u_{13} & u_{14}\\ u_{21} & u_{22} & u_{23} & u_{24}\\ u_{31} & u_{32} & u_{33} & u_{34}\\ u_{41} & u_{42} & u_{43} & u_{44} \end{array} \right ),$

то вычисляются:

$T:=\left ( \begin{array}{cc} u_{11} & u_{12}\\ u_{21} & u_{22} \end{array} \right )^{-1} = \left ( \begin{array}{cc} t_{11} & t_{12}\\ t_{21} & t_{22} \end{array} \right ),$

$R:= \left ( \begin{array}{cc} u_{31} & u_{32}\\ u_{41} & u_{42} \end{array} \right ) \left ( \begin{array}{cc} t_{11} & t_{12}\\ t_{21} & t_{22} \end{array} \right ) =\left ( \begin{array}{cc} r_{11} & r_{12}\\ r_{21} & r_{22} \end{array} \right ).$


Теперь векторы $\textbf{c} $ записываются:

$\textbf{c}_{x,I} = \left ( \begin{array}{c} 1\\ 0\\ 0\\ 0 \end{array} \right ),\quad \textbf{c}_{x,R} = \left ( \begin{array}{c} 0\\ 0\\ r_{11}\\ r_{21} \end{array} \right ),\quad \textbf{c}_{x,T} = \left ( \begin{array}{c} t_{11}\\ t_{21}\\ 0 \\ 0 \end{array} \right ), $

$\textbf{c}_{y,I}= \left ( \begin{array}{c} 0\\ 1\\ 0\\ 0 \end{array} \right ),\quad \textbf{c}_{y,R}= \left ( \begin{array}{c} 0\\ 0\\ r_{12}\\ r_{22} \end{array} \right ),\quad \textbf{c}_{y,T} = \left ( \begin{array}{c} t_{12}\\ t_{22}\\ 0\\ 0 \end{array} \right ).$



2.7. Вычисление векторов $\textbf{a} $


Плоская поляризация Формулы для вычисления:

$\textbf{a}_{x,I}=[0\rangle\textbf{c}_{x,I},\quad \textbf{a}_{x,R}=[0\rangle\textbf{c}_{x,R},\quad \textbf{a}_{x,T}=[L\rangle\textbf{c}_{x,T}.$

$\textbf{a}_{y,I}=[0\rangle\textbf{c}_{y,I},\quad \textbf{a}_{y,R}=[0\rangle\textbf{c}_{y,R},\quad \textbf{a}_{y,T}=[L\rangle\textbf{c}_{y,T}.$

Здесь

$ [L\rangle = \left ( \begin{array}{cccc} e^{-i\omega\rho_L L} & 0 & e^{i\omega\rho_L L} & 0\\ 0 & e^{-i\omega\rho_L L} & 0 & e^{i\omega\rho_L L} \\ 0 & -e^{-i\omega\rho_L L}\cdot\rho_L/\mu_L & 0 & e^{i\omega\rho_L L}\cdot\rho_L/\mu_L \\ e^{-i\omega\rho_L L}\cdot\rho_L/\mu_L & 0 & -e^{i\omega\rho_L L}\cdot\rho_L/\mu_L & 0 \end{array} \right ),$

$[0\rangle = \langle 0]^{-1} = \left ( \begin{array}{cccc} 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1 \\ 0 & -\rho_0/\mu_0 & 0 & \rho_0/\mu_0 \\ \rho_0/\mu_0 & 0 & -\rho_0/\mu_0 & 0 \end{array} \right ),$

при $\rho_L = \sqrt{\varepsilon_L\mu_L}$, $\rho_0 = \sqrt{\varepsilon_0\mu_0}$.

Круговая поляризация Формулы для вычисления:

$\textbf{a}_{r,I}=\textbf{a}_{x,I}+i\textbf{a}_{y,I},\quad \textbf{a}_{r,R}=\textbf{a}_{x,R}+i\textbf{a}_{y,R},\quad \textbf{a}_{r,T}=\textbf{a}_{x,T}+i\textbf{a}_{y,T}.$

$\textbf{a}_{l,I}=\textbf{a}_{x,I}-i\textbf{a}_{y,I},\quad \textbf{a}_{l,R}=\textbf{a}_{x,R}-i\textbf{a}_{y,R},\quad \textbf{a}_{l,T}=\textbf{a}_{x,T}-i\textbf{a}_{y,T}.$



2.8. Вычисление коэффициента отражения $R$ и коэффициента прохождения $T$


Вектор $\textbf{a}$ имеет структуру:

$\textbf{a} := \left ( \begin{array}{c} e_x\\ e_y\\ h_x\\ h_y \end{array} \right ),$

Плотность потока энергии определяется $\langle\textbf{S}\rangle$ — вектором Пойнтинга, усредненным по периоду колебаний:

$\left\langle \textbf{S}(t)\right\rangle = \left\langle\operatorname{Re}[\textbf{E}] \times \operatorname{Re}[\textbf{H}]\right\rangle=\frac{1}{4}\left( \textbf{e} \times \textbf{h}^*+\textbf{e}^* \times \textbf{h} \right), $

где звездочкой ${}^*$ обозначено комплексное сопряжение.

Используя эту формулу вычисляются

$\begin{array}{c} \displaystyle \langle\textbf{S}\rangle_{I,\alpha}:=\langle\textbf{S}\rangle(\textbf{a}_{\alpha,I}),\\ \displaystyle \langle\textbf{S}\rangle_{T,\alpha}:=\langle\textbf{S}\rangle(\textbf{a}_{\alpha,T}),\\ \displaystyle \langle\textbf{S}\rangle_{R,\alpha}:=\langle\textbf{S}\rangle(\textbf{a}_{\alpha,R}), \end{array}$

где $\alpha$ принимает значения $x,y$ (падают волны плоской поляризации) либо $r,l$ (падают волны круговой поляризации).

Для нахождения коэффициента отражения $R$ и коэффициента прохождения $T$ используются формулы:

$T_{\alpha}=\frac{|\langle\textbf{S}\rangle_{T,\alpha}|}{| \langle\textbf{S}\rangle_{I,\alpha}|}, \quad R_{\alpha}=\frac{|\langle\textbf{S}\rangle_{R,\alpha}|}{| \langle\textbf{S}\rangle_{I,\alpha}|}.$



3. Заключение


Ну вот. Теперь можно применять. Инструмент забавный. Всем добра.
Поделиться с друзьями
-->

Комментарии (31)


  1. Shkaff
    04.05.2017 16:25
    #10045589
    +3

    Я все понимаю, полезное упражнение, хорошо второкурсникам давать, но что это делает тут? Без объяснений и какого либо сопровождающего текста?


    1. FransuaMaryDelone
      05.05.2017 07:40
      #10046881
      -1

      Статья ориентирована на тех, кто захочет написать код функции, поэтому без математических выкладок — всё в стиле «делай, не думай».


      1. Shkaff
        05.05.2017 10:47
        #10047267
        +2

        Ну отлично, давайте теперь все задачки из Ландау Лифшица постить тут, просто на случай кому-то понадобится.


        1. FransuaMaryDelone
          05.05.2017 12:21
          #10047601
          -2

          Укажите пожалуйста на внешний источник, откуда я мог бы, по-Вашему, скопировать содержание статьи.


          1. Shkaff
            05.05.2017 12:32
            #10047645
            +1

            Я не говорю, что вы скопировали, просто это все настолько стандартно, что без словесного описания совершенно неинтересно.


            1. FransuaMaryDelone
              05.05.2017 12:40
              #10047669
              -2

              Стандартно в каком смысле? Покажите этот стандарт, на который Вы ссылаетесь.


              1. Shkaff
                05.05.2017 12:44
                #10047691
                +1

                В том смысле, что в любом учебнике для вузов по ЭМ написано, как это делать, а в более специальных книгах по оптике напрямую вычисляется. Это стандартная техника построения многослойных покрытий зеркал, например, и описана в куче публикаций и книг, мне лень гуглить.


                1. FransuaMaryDelone
                  05.05.2017 13:07
                  #10047773
                  -2

                  мне лень гуглить
                  А я Вам помогу:
                  1. Кац
                  2. Озеен: C. W. Oseen, «Beitraige zur Theorie der anisotropen Flissigkeiten,» Ark. Mat. Astron. Fys. A 21, 14-35 (1925),
                  3. Вохлер: https://doi.org/10.1364/JOSAA.5.001554

                  Там одна холесерическая пластина (без магнитной проницаемости и поглощения).

                  любом учебнике для вузов по ЭМ написано, как это делать, а в более специальных книгах по оптике напрямую вычисляется
                  Что вычисляется? Стопка холестерических пластин с дихроизмом? Да где же этот учебник?! Как жаль, что Вам лень гуглить.


                  1. Shkaff
                    05.05.2017 13:42
                    #10047865
                    +1

                    Вы знаете, после вашего отношения к комментариям никакого желания вести с вами обсуждение нет, даже если вы и правы в том, что такие подробности в вузовском учебнике не встретишь.


                    1. FransuaMaryDelone
                      05.05.2017 14:48
                      #10048021
                      -3

                      Это говорит лишь о том, что Вам нечем крыть. То-есть, написали херню, а теперь в кусты.


                      1. Shkaff
                        05.05.2017 14:51
                        #10048031
                        +1

                        Хахах, вы смешной:) Наверное, "делай, не думай" — ваш девиз по жизни.


                        1. FransuaMaryDelone
                          05.05.2017 14:58
                          #10048051
                          -3

                          ха-ха-ха. (это я над Вами, тупорылым, ведь если карма у меня занулится, с кем Вам придется тут спорить?)


                    1. FransuaMaryDelone
                      05.05.2017 15:07
                      #10048075
                      -3

                      никакого желания вести с вами обсуждение нет
                      Это у меня нет желания разговаривать с людьми, которые ничего не понимают, но корчат из себя знающих. Но смотрите — я разговариваю с Вами.) терплю дураков.


        1. FransuaMaryDelone
          05.05.2017 12:30
          #10047635
          -2

          постить тут, просто на случай кому-то понадобится.
          А это что еще за хрень? Мне, например, не нравятся Ваши статьи. Мне они не понадобятся. Вам тоже чтоли не надо их постить? — Это не аргумент. Я буду постить тут то, что мне интересно, не обращая внимания на подобный писк, оставляя за Вами право писать то, что интересно Вам.


          1. Shkaff
            05.05.2017 12:33
            #10047655
            +1

            Ну, а за мной остается право писать к ним комменты, выражая свое по их поводу мнение.


            1. FransuaMaryDelone
              05.05.2017 14:57
              #10048045
              -3

              да-да, смешивая себя с говном.


  1. Mulin
    04.05.2017 17:51
    #10045865
    -3

    Слишком много матана…


  1. hardegor
    04.05.2017 18:57
    #10046027
    +2

    До ката всё понятно. А после ката, наверное, только специалист разберется.
    Лучше бы привели пример расчета для 1.5, 2, 10 и 50 пластинок, тогда хотя бы понятно стало, что это за формулы и как их применять в жизни или работе :)


  1. ivlis
    05.05.2017 01:39
    #10046701
    +2

    Чего-то у вас сложно. Должна быть одна матрица 4x4 которая описывает рассеяние фотонов на границе между двумя диэлектриками и одна матрица переноса. Поляризации можно выбрать любые, хоть плоские, хоть круговые, от этого только коэффициенты изменяется. Откуда у вас все 4 сразу? :)

    Ну и как отметили выше — не понятно зачем оно нужно.


    1. FransuaMaryDelone
      05.05.2017 07:53
      #10046891
      -4

      Чего-то у вас сложно. Должна быть одна матрица 4x4 которая описывает рассеяние фотонов на границе между двумя диэлектриками и одна матрица переноса.
      Ну сложно если Вам, то идите на второй курс учиться. Матрица тут вообще одна — описывает «рассеяние фотонов сразу на всей на стопке» (п.2.6), если угодно. Ну и для границы диэлектриков, если уж на то пошло, достаточно матрицы 2х2, а не 4х4 как Вы заявляете. Идите учиться, не пукайте тут.


      1. ivlis
        05.05.2017 09:35
        #10047069
        +3

        FransuaMaryDelone принимает научную критику за личное оскорбление. Это тупо. Не будь как
        FransuaMaryDelone.

        Пространство динамических уравнений Максвелла четырехмерное, поэтому амплитуды будет четыре, конечно. Не помню на каком курсе это проходят.


        1. FransuaMaryDelone
          05.05.2017 10:41
          #10047253
          -5

          Ваши слова не являются научной критикой, они являются следствием Вашей безграмотности, и в моем предыдущем сообщении есть аргументы на этот счет. В безграмотности самой по себе нет ничего плохого. Плохо начинается тогда, когда дурак начинает считать себя умным.


          1. ivlis
            05.05.2017 19:13
            #10048587
            +3

            Второе золотое правило: переходя на личности — выясни личность. У меня есть публикации по электродинамике, в т.ч. про пластины в т.ч. в гиротропией. :)


            1. FransuaMaryDelone
              06.05.2017 21:40
              #10049649
              -2

              У меня есть публикации
              Это позорище — трясти публикациями — Вам больше нечем удивить оппонента. Ну и потом Вы не указали:
              1. импакт-фактор журнала,
              2. количество соавторов,
              3. сколько раз на Ваши статьи ссылались другие авторы (кроме Вас).

              Впрочем, судя по эпитету «динамические», которым Вы снабдили уравнения Максвелла, и по тому, что Вы настаиваете на том, что в одномерном случае в изотропных средах необходимо не 2, а 4 различных «амплитуды» (как Вы их назвали странно), могу предположить, что опубликовались Вы в трудах какой-нибудь непрофильной конференции или в «вестнике Мусохранского ПТУ» или в соавторы Вы попали случайно. Специализация Ваша далека от электродинамики. В любом случае намеки на авторство научных статей при таких пробелах в образовании и при таких обстоятельствах разговора выглядят позорно и жалко.


  1. Turbojihad
    05.05.2017 07:34
    #10046877

    Зачем это здесь?


    1. FransuaMaryDelone
      05.05.2017 08:04
      #10046899
      -4

      А Вы тут зачем? Какой от Вас толк?


  1. Dioxin
    05.05.2017 07:56
    #10046895

    И где хваленая песочница? СПАМ.


  1. Rumlin
    05.05.2017 08:08
    #10046905
    +2

    Собственно не хватает применения, расчетов для интересных случаев.


    1. FransuaMaryDelone
      05.05.2017 08:13
      #10046915
      -2

      какие случаи Вам кажутся интересными?


      1. Rumlin
        05.05.2017 08:23
        #10046927
        +2

        Вам виднее — вам известно для каких случаев это применимо. Хотя бы хотелось бы увидеть анонс:

        Ну а как строить-то такую характеристику? А если пластинки поглощающие? А вдруг они еще и анизотропные некоторые? А если не просто анизотропные, а прям холестерические, как в жидкокристаллических мониторах?


        1. FransuaMaryDelone
          05.05.2017 08:30
          #10046951
          -4

          Вам виднее
          А, Вы в этом смысле… Спасибо за совет.