Метод Нелдера — Мида — метод оптимизации (поиска минимума) функции от нескольких переменных. Простой и в тоже время эффективный метод, позволяющий оптимизировать функции без использования градиентов. Метод надежен и, как правило, показывает замечательные результаты, хотя и отсутствует теория сходимости. Может использоваться в функции optimize из модуля scipy.optimize популярной библиотеки для языка python, которая используется для математических расчетов.

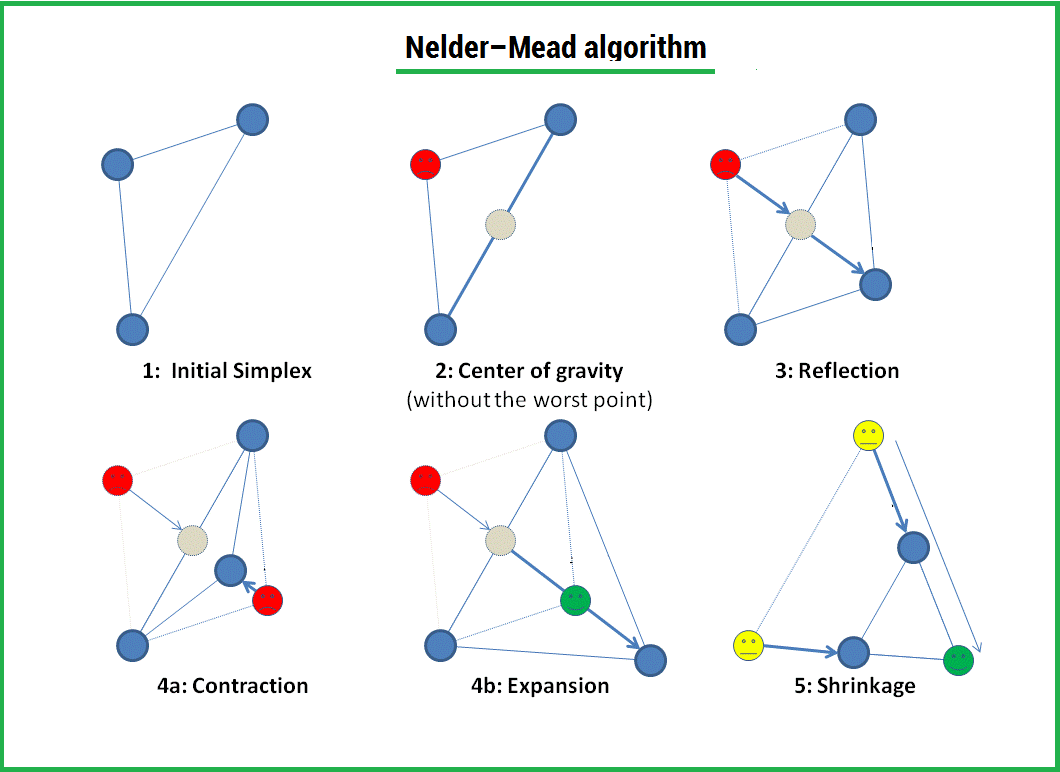
Алгоритм заключается в формировании симплекса (simplex) и последующего деформирования в направлении минимума, посредством трех операций:

1) Отражение (reflection);
2) Растяжения (expansion);
3) Сжатие (contract);

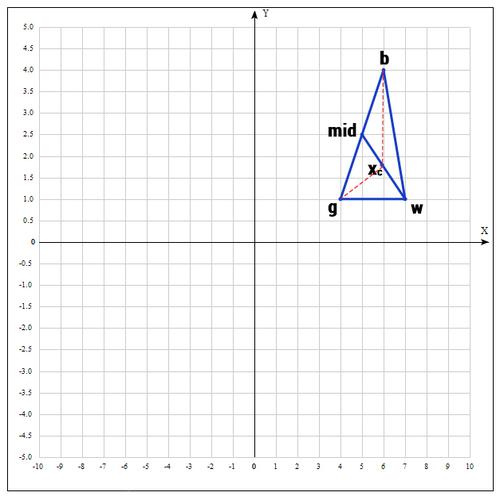
Симплекс представляет из себя геометрическую фигуру, являющуюся n — мерным обобщением треугольника. Для одномерного пространства — это отрезок, для двумерного — треугольник. Таким образом n — мерный симплекс имеет n + 1 вершину.

Алгоритм

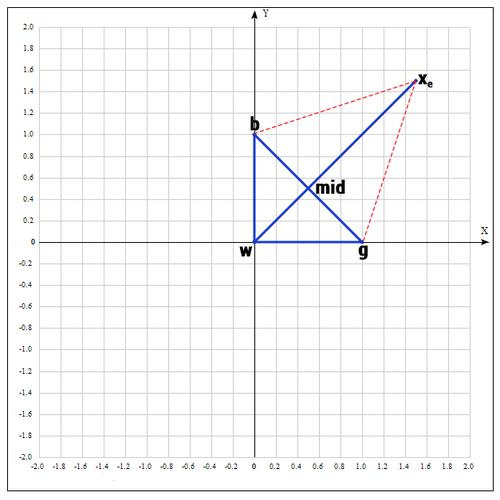
1) Пусть $$ функция, которую необходимо оптимизировать. На первом шаге выбираем три случайные точки (об этом чуть позже) и формируем симплекс (треугольник). Вычисляем значение функции в каждой точке: $$, $$, $$.

Сортируем точки по значениям функции $$ в этих точках, т.е. получаем двойное неравенство: $$ ? $$ ? $$.

Мы ищем минимум функции, а следовательно, на данном шаге лучшей будет та точка, в которой значение функции минимально. Для удобства переобозначим точки следующим образом:
b = $$, g = $$, w = $$, где best, good, worst — соответственно.



2) На следующем шаге находим середину отрезка, точками которого являются g и b. Т.к. координаты середины отрезка равны полусумме координат его концов, получаем:

$$

В более общем виде можно записать так:

$$

3) Применяем операцию отражения:
Находим точку $$, следующим образом:

$$

Т.е. фактически отражаем точку w относительно mid. В качестве коэффициента берут как правило 1. Проверяем нашу точку: если f($$) < f(g), то это хорошая точка. А теперь попробуем расстояние увеличить в 2 раза, вдруг нам повезет и мы найдем точку еще лучше.



4) Применяем операцию растяжения:
Находим точку $$ следующим образом:

$$

В качестве ? принимаем ? = 2, т.е. расстояние увеличиваем в 2 раза.

Проверяем точку $$:

Если f($$) < f(b), то нам повезло и мы нашли точку лучше, чем есть на данный момент, если бы этого не произошло, мы бы остановились на точке $$.

Далее заменяем точку w на $$, в итоге получаем:



5) Если же нам совсем не повезло и мы не нашли хороших точек, пробуем операцию сжатия.
Как следует из названия операции мы будем уменьшать наш отрезок и искать хорошие точки внутри треугольника.

Пробуем найти хорошую точку $$:

$$

Коэффициент ? принимаем равным 0.5, т.е. точка $$ на середине отрезка wmid.



Существует еще одна операция — shrink (сокращение). В данном случае, мы переопределяем весь симплекс. Оставляем только «лучшую» точку, остальные определяем следующим образом:

$$

Коэффициент ? берут равным 0.5.

По существу передвигаем точки по направлению к текущей «лучшей» точке. Преобразование выглядит следующим образом:



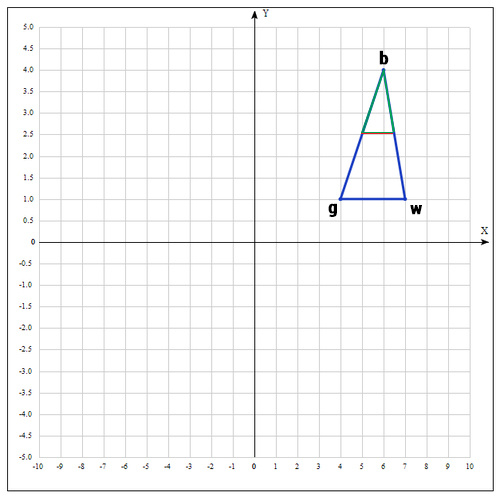
Необходимо отметить, что данная операция дорого обходится, поскольку необходимо заменять точки в симплексе. К счастью было установлено, при проведении большого количества экспериментов, что shrink — трансформация редко случается на практике.

Алгоритм заканчивается, когда:

1) Было выполнено необходимое количество итераций.
2) Площадь симплекса достигла определенной величины.
3) Текущее лучшее решение достигло необходимой точности.

Как и в большинстве эвристических методов, не существует идеального способа выбора инициализирующих точек. Как уже было сказано, можно брать случайные точки, находящиеся недалеко друг от друга для формирования симплекса; но есть решение и получше, которое используется в реализации алгоритма в MATHLAB:

Выбор первой точки $$ поручаем пользователю, если он имеет некоторое представление о возможном хорошем решении, в противном случае выбирается случайным образом. Остальные точки выбираются исходя из $$, на небольшом расстоянии вдоль направления каждого измерения:

$$

где $$ — единичный вектор.
$$ определяется таким образом:
$$ = 0.05, если коэффициент при $$ в определении $$ не нулевой.
$$ = 0.00025, если коэффициент при $$ в определении нулевой.

Пример:

Найти экстремум следующей функции: $$

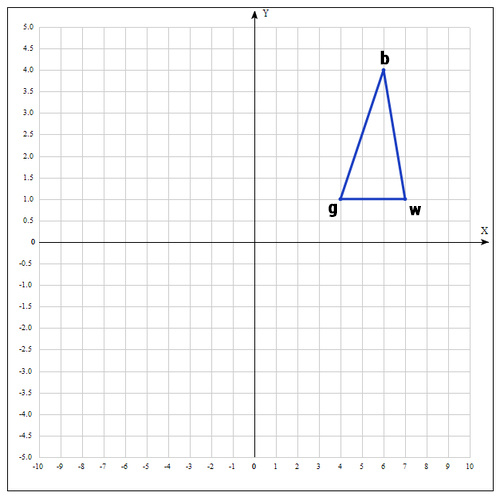
В качестве начальных возьмем точки:

$$

Вычислим значение функции в каждой точке:

$$
$$
$$

Переобозначим точки следующим образом:

$$

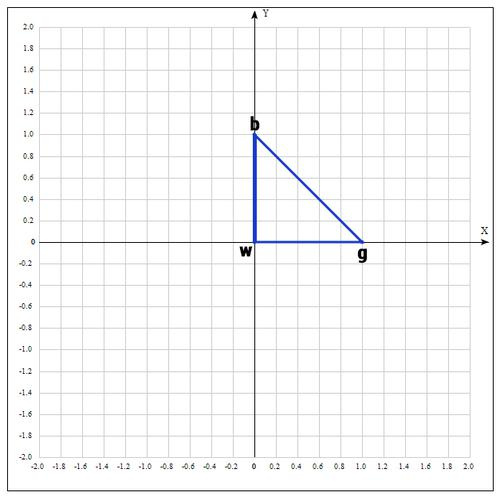
Находим середину отрезка bg:

$$

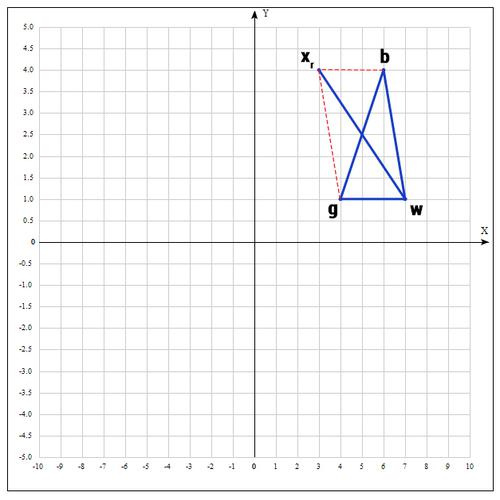
Находим точку $$ (операция отражения):

$$

если ?=1, тогда:

$$

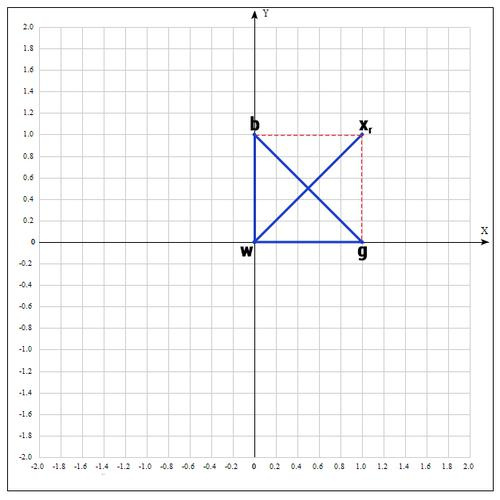
Проверяем точку $$:

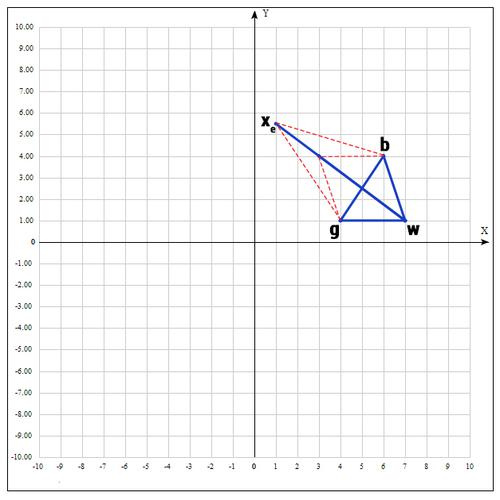
$$, т.к. $$ пробуем увеличить отрезок (операция растяжения).

$$

если ? = 2, тогда:

$$

$$

Проверяем значение функции в точке $$:

$$

Оказалось, что точка $$ «лучше» точки b. Следовательно мы получаем новые вершины:

$$

И алгоритм начинается сначала.

Таблица значений для 10 итераций:

Best	Good	Worst
$$	$$	$$
$$	$$	$$
$$	$$	$$
$$	$$	$$
$$	$$	$$
$$	$$	$$
$$	$$	$$
$$	$$	$$
$$	$$	$$
$$	$$	$$

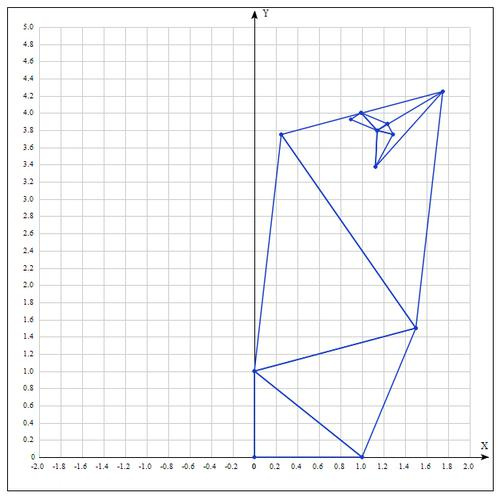
Аналитически находим экстремум функции, он достигается в точке $$.
После 10 итераций мы получаем достаточно точное приближение: $$

Еще о методе:

Алгоритм Нелдера — Мида в основном используется для выбора параметра в машинном обучении. В сущности, симплекс метод используется для оптимизации параметров модели. Это связано с тем, что данный метод оптимизирует целевую функцию довольно быстро и эффективно (особенно там, где не используется shrink — модификация).

С другой стороны, в силу отсутствия теории сходимости, на практике метод может приводить к неверному ответу даже на гладких (непрерывно дифференцируемых) функциях. Также возможна ситуация, когда рабочий симплекс находится далеко от оптимальной точки, а алгоритм производит большое число итераций, при этом мало изменяя значения функции. Эвристический метод решения этой проблемы заключается в запуске алгоритма несколько раз и ограничении числа итераций.

Реализация на языке программирования python:

Создаем вспомогательный класс Vector и перегружаем операторы для возможности производить с векторами базовые операции. Я намерено не использовал вспомогательные библиотеки для реализации алгоритма, т.к. в таком случае зачастую снижается восприятие.

class Vector(object):
    def __init__(self, x, y):
        """ Create a vector, example: v = Vector(1,2) """
        self.x = x
        self.y = y

    def __repr__(self):
        return "({0}, {1})".format(self.x, self.y)

    def __add__(self, other):
        x = self.x + other.x
        y = self.y + other.y
        return Vector(x, y)

    def __sub__(self, other):
        x = self.x - other.x
        y = self.y - other.y
        return Vector(x, y)

    def __mul__(self, other):
        x = self.x * other
        y = self.y * other
        return Vector(x, y)

    def __truediv__(self, other):
        x = self.x / other
        y = self.y / other
        return Vector(x, y)

    def c(self):
        return (self.x, self.y)
        


def f(point):
    x, y = point
    return x**2 + x*y + y**2 - 6*x - 9*y

def nelder_mead(alpha=1, beta=0.5, gamma=2):
    v1 = Vector(0, 0)
    v2 = Vector(1.0, 0)
    v3 = Vector(0, 1)

    for i in range(10):
        adict = {v1:f(v1.c()), v2:f(v2.c()), v3:f(v3.c())}
        points = sorted(adict.items(), key=lambda x: x[1])
        b = points[0][0]
        g = points[1][0]
        w = points[2][0]
        
        mid = (g + b)/2
        xr = mid * 2 - w
        if f(xr.c()) < f(g.c()):
            w = xr
        else:
            if f(xr.c()) < f(w.c()):
                w = xr
            c = (w + mid)/2
            if f(c.c()) < f(w.c()):
                w = c
        if f(xr.c()) < f(b.c()):
            xe = xr * 2 - mid
            if f(xe.c()) < f(xr.c()):
                w = xe
            else:
                w = xr
        if f(xr.c()) > f(g.c()):
            xc = mid * (1 - beta) + w * beta
            if f(xc.c()) < f(w.c()):
                w = xc
        v1 = w
        v2 = g
        v3 = b
    print(b)
        
nelder_mead()

P.S. Может у кого-нибудь есть реализация алгоритма на других языках программирования? С радостью расширю статью, естественно указав автора реализации.

Спасибо за чтение статьи. Надеюсь она была Вам полезна и Вы узнали много нового.
С вами был FUNNYDMAN. Удачной оптимизации!)