Екатерина Малахова, редактор-фрилансер, специально для блога Нетологии адаптировала статью Beau Carnes об основных типах структур данных.

«Плохие программисты думают о коде. Хорошие программисты думают о структурах данных и их взаимосвязях», — Линус Торвальдс, создатель Linux.

Структуры данных играют важную роль в процессе разработки ПО, а еще по ним часто задают вопросы на собеседованиях для разработчиков. Хорошая новость в том, что по сути они представляют собой всего лишь специальные форматы для организации и хранения данных.

В этой статье я покажу вам 10 самых распространенных структур данных. Для каждой из них приведены видео и примеры их реализации на JavaScript. Чтобы вы смогли попрактиковаться, я также добавил несколько упражнений из бета-версии новой учебной программы freeCodeCamp.

Обратите внимание, что некоторые структуры данных включают временную сложность в нотации «большого О». Это относится не ко всем из них, так как иногда временная сложность зависит от реализации. Если вы хотите узнать больше о нотации «большого О», посмотрите это видео от Briana Marie.

В статье я привожу примеры реализации этих структур данных на JavaScript: они также пригодятся, если вы используете низкоуровневый язык вроде С. В многие высокоуровневые языки, включая JavaScript, уже встроены реализации большинства структур данных, о которых пойдет речь. Тем не менее, такие знания станут серьезным преимуществом при поиске работы и пригодятся при написании высокопроизводительного кода.

Связные списки

Связный список — одна из базовых структур данных. Ее часто сравнивают с массивом, так как многие другие структуры можно реализовать с помощью либо массива, либо связного списка. У этих двух типов есть преимущества и недостатки.


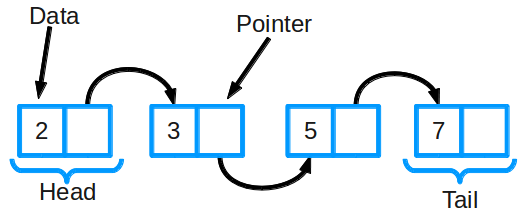
Так устроен связный список

Связный список состоит из группы узлов, которые вместе образуют последовательность. Каждый узел содержит две вещи: фактические данные, которые в нем хранятся (это могут быть данные любого типа) и указатель (или ссылку) на следующий узел в последовательности. Также существуют двусвязные списки: в них у каждого узла есть указатель и на следующий, и на предыдущий элемент в списке.

Основные операции в связном списке включают добавление, удаление и поиск элемента в списке.

Пример реализации на JavaScript

Временная сложность связного списка
г===========T=================T===============¬
¦ Алгоритм  ¦Среднее значение ¦ Худший случай ¦
¦===========+=================+===============¦
¦ Space     ¦ O(n)            ¦ O(n)          ¦
¦ Search    ¦ O(n)            ¦ O(n)          ¦
¦ Insert    ¦ O(1)            ¦ O(1)          ¦
¦ Delete    ¦ O(1)            ¦ O(1)          ¦
L===========¦=================¦===============-

Упражнения от freeCodeCamp

• Work with Nodes in a Linked List
• Create a Linked List Class
• Remove Elements from a Linked List
• Search within a Linked List
• Remove Elements from a Linked List by Index
• Add Elements at a Specific Index in a Linked List
• Create a Doubly Linked List
• Reverse a Doubly Linked List

Стеки

Стек — это базовая структура данных, которая позволяет добавлять или удалять элементы только в её начале. Она похожа на стопку книг: если вы хотите взглянуть на книгу в середине стека, сперва придется убрать лежащие сверху.

Стек организован по принципу LIFO (Last In First Out, «последним пришёл — первым вышел»)?. Это значит, что последний элемент, который вы добавили в стек, первым выйдет из него.


Так устроен стек

В стеках можно выполнять три операции: добавление элемента (push), удаление элемента (pop) и отображение содержимого стека (pip).

Пример реализации на JavaScript

Временная сложность стека
г===========T=================T===============¬
¦ Алгоритм  ¦Среднее значение ¦ Худший случай ¦
¦===========+=================+===============¦
¦ Space     ¦ O(n)            ¦ O(n)          ¦
¦ Search    ¦ O(n)            ¦ O(n)          ¦
¦ Insert    ¦ O(1)            ¦ O(1)          ¦
¦ Delete    ¦ O(1)            ¦ O(1)          ¦
L===========¦=================¦===============-

Упражнения от freeCodeCamp

• Learn how a Stack Works
• Create a Stack Class

Очереди

Эту структуру можно представить как очередь в продуктовом магазине. Первым обслуживают того, кто пришёл в самом начале — всё как в жизни.


Так устроена очередь

Очередь устроена по принципу FIFO (First In First Out, «первый пришёл — первый вышел»). Это значит, что удалить элемент можно только после того, как были убраны все ранее добавленные элементы.

Очередь позволяет выполнять две основных операции: добавлять элементы в конец очереди (enqueue) и удалять первый элемент (dequeue).

Пример реализации на JavaScript

Временная сложность очереди
г===========T=================T===============¬
¦ Алгоритм  ¦Среднее значение ¦ Худший случай ¦
¦===========+=================+===============¦
¦ Space     ¦ O(n)            ¦ O(n)          ¦
¦ Search    ¦ O(n)            ¦ O(n)          ¦
¦ Insert    ¦ O(1)            ¦ O(1)          ¦
¦ Delete    ¦ O(1)            ¦ O(1)          ¦
L===========¦=================¦===============-

Упражнения от freeCodeCamp

• Create a Queue Class
• Create a Priority Queue Class
• Create a Circular Queue

Множества

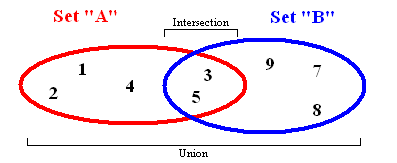
Так выглядит множество

Множество хранит значения данных без определенного порядка, не повторяя их. Оно позволяет не только добавлять и удалять элементы: есть ещё несколько важных функций, которые можно применять к двум множествам сразу.

• Объединение комбинирует все элементы из двух разных множеств, превращая их в одно (без дубликатов).
• Пересечение анализирует два множества и ?создает еще одно из тех элементов, которые присутствуют в обоих изначальных множествах.
• Разность выводит список элементов, которые есть в одном множестве, но отсутствуют в другом.
• Подмножество выдает булево значение, которое показывает, включает ли одно множество все элементы другого множества.

Пример реализации на JavaScript

Упражнения от freeCodeCamp

• Create a Set Class
• Remove from a Set
• Size of the Set
• Perform a Union on Two Sets
• Perform an Intersection on Two Sets of Data
• Perform a Difference on Two Sets of Data
• Perform a Subset Check on Two Sets of Data
• Create and Add to Sets in ES6
• Remove items from a set in ES6
• Use .has and .size on an ES6 Set
• Use Spread and Notes for ES5 Set() Integration

Map

Map — это структура, которая хранит данные в парах ключ/значение, где каждый ключ уникален. Иногда её также называют ассоциативным массивом или словарём. Map часто используют для быстрого поиска данных. Она позволяет делать следующие вещи:

• добавлять пары в коллекцию;
• удалять пары из коллекции;
• изменять существующей пары;
• искать значение, связанное с определенным ключом.

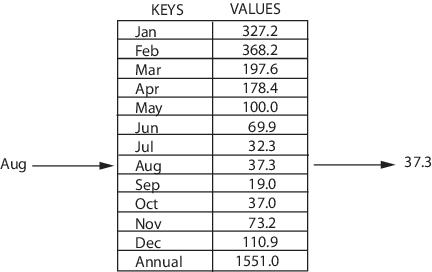
Так устроена структура map

Пример реализации на JavaScript

Упражнения от freeCodeCamp

• Create a Map Data Structure
• Create an ES6 JavaScript Map

Хэш-таблицы

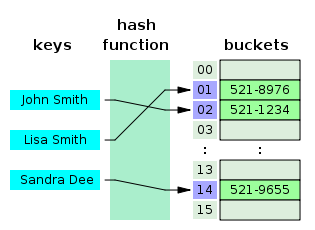
Так работают хэш-таблица и хэш-функция

Хэш-таблица — это похожая на Map структура, которая содержит пары ключ/значение. Она использует хэш-функцию для вычисления индекса в массиве из блоков данных, чтобы найти желаемое значение.

Обычно хэш-функция принимает строку символов в качестве вводных данных и выводит числовое значение. Для одного и того же ввода хэш-функция должна возвращать одинаковое число. Если два разных ввода хэшируются с одним и тем же итогом, возникает коллизия. Цель в том, чтобы таких случаев было как можно меньше.

Таким образом, когда вы вводите пару ключ/значение в хэш-таблицу, ключ проходит через хэш-функцию и превращается в число. В дальнейшем это число используется как фактический ключ, который соответствует определенному значению. Когда вы снова введёте тот же ключ, хэш-функция обработает его и вернет такой же числовой результат. Затем этот результат будет использован для поиска связанного значения. Такой подход заметно сокращает среднее время поиска.

Пример реализации на JavaScript

Временная сложность хэш-таблицы
г===========T=================T===============¬
¦ Алгоритм  ¦Среднее значение ¦ Худший случай ¦
¦===========+=================+===============¦
¦ Space     ¦ O(n)            ¦ O(n)          ¦
¦ Search    ¦ O(1)            ¦ O(n)          ¦
¦ Insert    ¦ O(1)            ¦ O(n)          ¦
¦ Delete    ¦ O(1)            ¦ O(n)          ¦
L===========¦=================¦===============-

Упражнения от freeCodeCamp

• Create a Hash Table

Двоичное дерево поиска

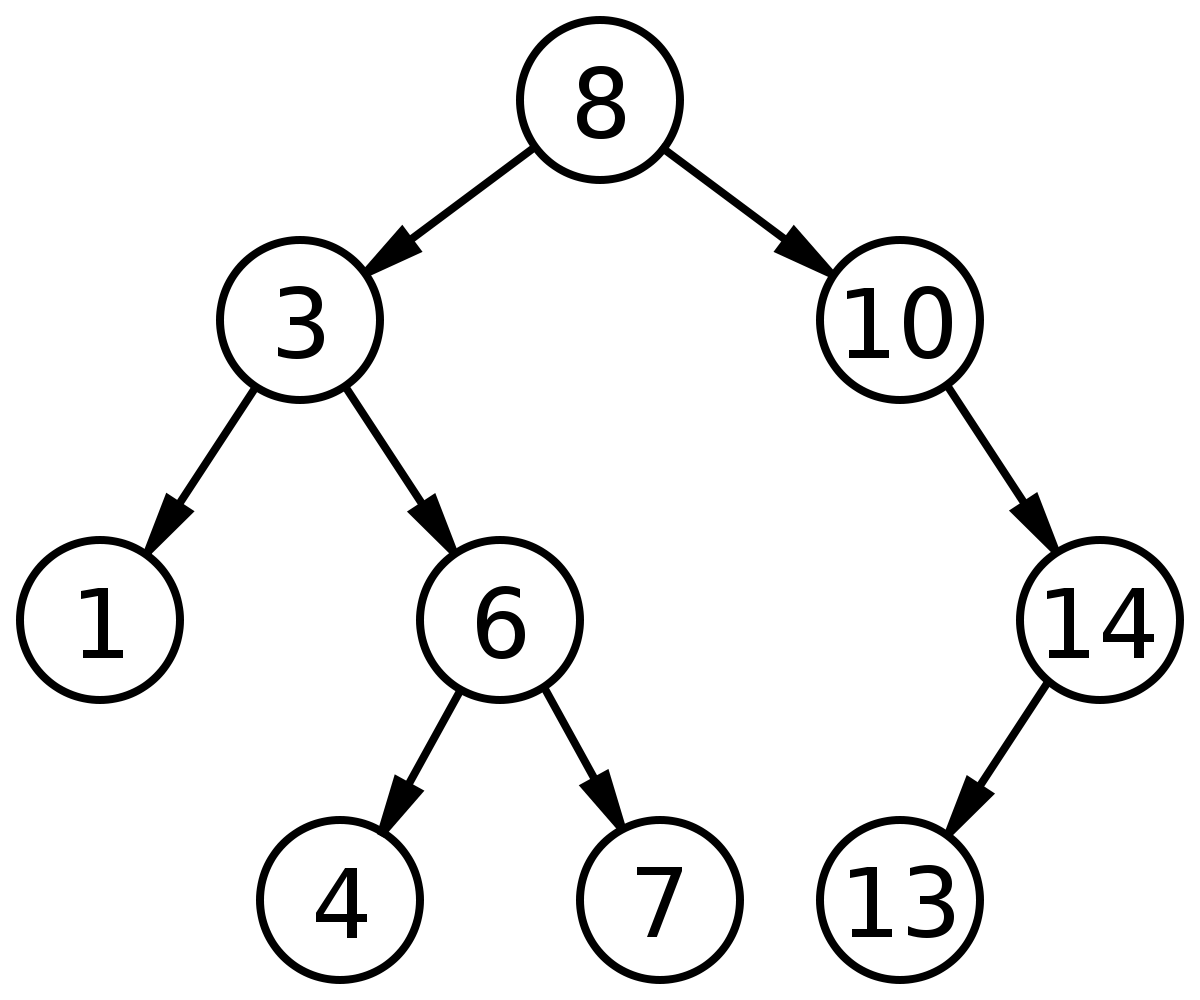
Двоичное дерево поиска

Дерево — это структура данных, состоящая из узлов. Ей присущи следующие свойства:

• Каждое дерево имеет корневой узел (вверху).
• Корневой узел имеет ноль или более дочерних узлов.
• Каждый дочерний узел имеет ноль или более дочерних узлов, и так далее.

У двоичного дерева поиска есть два дополнительных свойства:

• Каждый узел имеет до двух дочерних узлов (потомков).
• Каждый узел меньше своих потомков справа, а его потомки слева меньше его самого.

Двоичные деревья поиска позволяют быстро находить, добавлять и удалять элементы. Они устроены так, что время каждой операции пропорционально логарифму общего числа элементов в дереве.

Пример реализации на JavaScript

Временная сложность двоичного дерева поиска 
г===========T=================T==============¬
¦ Алгоритм  ¦Среднее значение ¦Худший случай ¦
¦===========+=================+==============¦
¦ Space     ¦ O(n)            ¦ O(n)         ¦
¦ Search    ¦ O(log n)        ¦ O(n)         ¦
¦ Insert    ¦ O(log n)        ¦ O(n)         ¦
¦ Delete    ¦ O(log n)        ¦ O(n)         ¦
L===========¦=================¦==============-

Упражнения от freeCodeCamp

• Find the Minimum and Maximum Value in a Binary Search Tree
• Add a New Element to a Binary Search Tree
• Check if an Element is Present in a Binary Search Tree
• Find the Minimum and Maximum Height of a Binary Search Tree
• Use Depth First Search in a Binary Search Tree
• Use Breadth First Search in a Binary Search Tree
• Delete a Leaf Node in a Binary Search Tree
• Delete a Node with One Child in a Binary Search Tree
• Delete a Node with Two Children in a Binary Search Tree
• Invert a Binary Tree

Префиксное дерево

Префиксное (нагруженное) дерево — это разновидность дерева поиска. Оно хранит данные в метках, каждая из которых представляет собой узел на дереве. Такие структуры часто используют, чтобы хранить слова и выполнять быстрый поиск по ним — например, для функции автозаполнения.



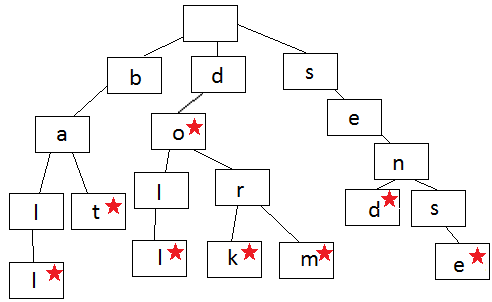
Так устроено префиксное дерево

Каждый узел в языковом префиксном дереве содержит одну букву слова. Чтобы составить слово, нужно следовать по ветвям дерева, проходя по одной букве за раз. Дерево начинает ветвиться, когда порядок букв отличается от других имеющихся в нем слов или когда слово заканчивается. Каждый узел содержит букву (данные) и булево значение, которое указывает, является ли он последним в слове.

Посмотрите на иллюстрацию и попробуйте составить слова. Всегда начинайте с корневого узла вверху и спускайтесь вниз. Это дерево содержит следующие слова: ball, bat, doll, do, dork, dorm, send, sense.

Пример реализации на JavaScript

Упражнения от freeCodeCamp

• Create a Trie Search Tree

Двоичная куча

Двоичная куча — ещё одна древовидная структура данных. В ней у каждого узла не более двух потомков. Также она является совершенным деревом: это значит, что в ней полностью заняты данными все уровни, а последний заполнен слева направо.


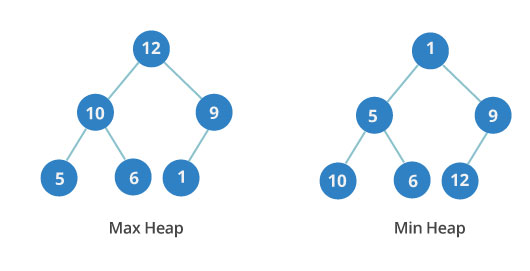
Так устроены минимальная и максимальная кучи

Двоичная куча может быть минимальной или максимальной. В максимальной куче ключ любого узла всегда больше ключей его потомков или равен им. В минимальной куче всё устроено наоборот: ключ любого узла меньше ключей его потомков или равен им.

Порядок уровней в двоичной куче важен, в отличие от порядка узлов на одном и том же уровне. На иллюстрации видно, что в минимальной куче на третьем уровне значения идут не по порядку: 10, 6 и 12.

Пример реализации на JavaScript

Временная сложность двоичной кучи
г===========T==================T===============¬
¦ Алгоритм  ¦ Среднее значение ¦ Худший случай ¦
¦===========+==================+===============¦
¦ Space     ¦ O(n)             ¦ O(n)          ¦
¦ Search    ¦ O(n)             ¦ O(n)          ¦
¦ Insert    ¦ O(1)             ¦ O(log n)      ¦
¦ Delete    ¦ O(log n)         ¦ O(log n)      ¦
¦ Peek      ¦ O(1)             ¦ O(1)          ¦
L===========¦==================¦===============-

Упражнения от freeCodeCamp

• Insert an Element into a Max Heap
• Remove an Element from a Max Heap
• Implement Heap Sort with a Min Heap

Граф

Графы — это совокупности узлов (вершин) и связей между ними (рёбер). Также их называют сетями.

По такому принципу устроены социальные сети: узлы — это люди, а рёбра — их отношения.



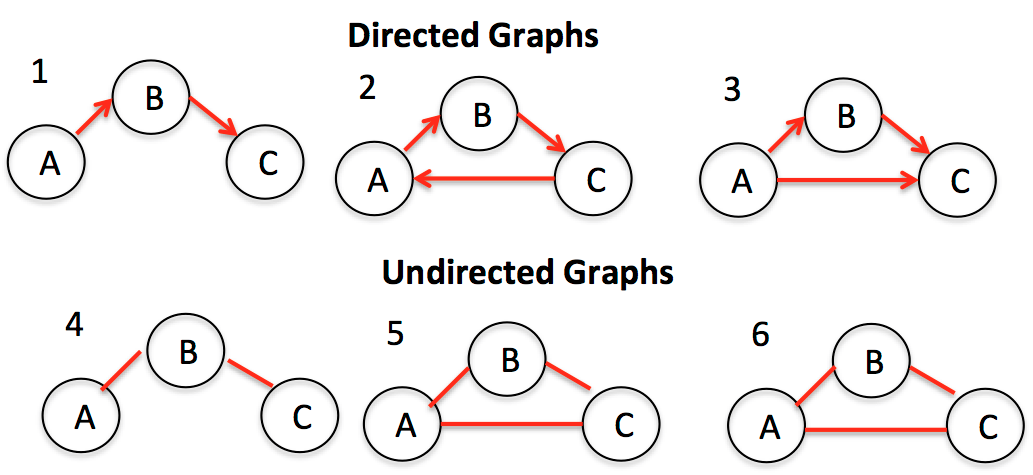
Графы делятся на два основных типа: ориентированные и неориентированные. У неориентированных графов рёбра между узлами не имеют какого-либо направления, тогда как у рёбер в ориентированных графах оно есть.

Чаще всего граф изображают в каком-либо из двух видов: это может быть список смежности или матрица смежности.


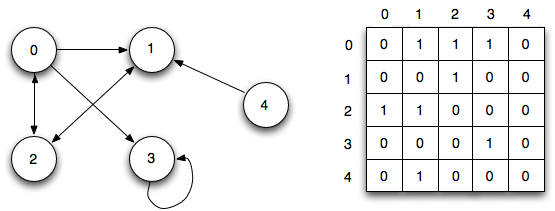
Граф в виде матрицы смежности

Список смежности можно представить как перечень элементов, где слева находится один узел, а справа — все остальные узлы, с которыми он соединяется.

Матрица смежности — это сетка с числами, где каждый ряд или колонка соответствуют отдельному узлу в графе. На пересечении ряда и колонки находится число, которое указывает на наличие связи. Нули означают, что она отсутствует; единицы — что связь есть. Чтобы обозначить вес каждой связи, используют числа больше единицы.

Существуют специальные алгоритмы для просмотра рёбер и вершин в графах — так называемые алгоритмы обхода. К их основным типам относят поиск в ширину (breadth-first search) и в глубину (depth-first search). Как вариант, с их помощью можно определить, насколько близко к корневому узлу находятся те или иные вершины графа. В видео ниже показано, как на JavaScript выполнить поиск в ширину.

Пример реализации на JavaScript

Временная сложность списка смежности (графа) 
г===============T============¬
¦   Алгоритм    ¦    Время   ¦
¦===============+============¦
¦ Storage       ¦ O(|V|+|E|) ¦
¦ Add Vertex    ¦ O(1)       ¦
¦ Add Edge      ¦ O(1)       ¦
¦ Remove Vertex ¦ O(|V|+|E|) ¦
¦ Remove Edge   ¦ O(|E|)     ¦
¦ Query         ¦ O(|V|)     ¦
L===============¦============-

Упражнения от freeCodeCamp

• Introduction to Graphs
• Adjacency List
• Adjacency Matrix
• Incidence Matrix
• Breadth-First Search
• Depth-First Search

Узнать больше

Если до этого вы никогда не сталкивались с алгоритмами или структурами данных, и у вас нет какой-либо подготовки в области ИТ, лучше всего подойдет книга Grokking Algorithms. В ней материал подан доступно и с забавными иллюстрациями (их автор — ведущий разработчик в Etsy), в том числе и по некоторым структурам данных, которые мы рассмотрели в этой статье.

От редакции Нетологии

Нетология проводит набор на курсы по Big Data:

1. Программа «Big Data: основы работы с большими массивами данных»

Для кого: инженеры, программисты, аналитики, маркетологи — все, кто только начинает вникать в технологию Big Data.

• введение в историю и основы технологии;
• способы сбора больших данных;
• типы данных;
• основные и продвинутые методы анализа больших данных;
• основы программирования, архитектуры хранения и обработки для работы с большими массивами данных.

Формат занятий: онлайн.

Подробности по ссылке > http://netolo.gy/dJd

2. Программа «Data Scientist»

Для кого: специалисты, работающие или собирающиеся работать с Big Data, а также те, кто планирует построить карьеру в области Data Science. Для обучения необходимо владеть как минимум одним из языков программирования (желательно Python) и помнить программу по математике старших классов (а лучше вуза).

Темы курса:

• экспресс-обучение основным инструментам, Hadoop, кластерные вычисления;
• деревья решений, метод k-ближайших соседей, логистическая регрессия, кластеризация;
• уменьшение размерности данных, методы декомпозиции, спрямляющие пространства;
• введение в рекомендательные системы;
• распознавание изображений, машинное зрение, нейросети;
• обработка текста, дистрибутивная семантика, чатботы;
• временные ряды, модели ARMA/ARIMA, сложные модели прогнозирования.

Формат занятий: офлайн, г. Москва, центр Digital October. Преподают специалисты из Yandex Data Factory, Ростелеком, «Сбербанк-Технологии», Microsoft, OWOX, Clever DATA, МТС.

Подробности по ссылке.