1) шар на пружине, ньютоновская версия
2) квантовый шар на пружине
3) волны, классический вид
4) волны, классическое уравнение движения
5) квантовые волны
6) поля
На самом деле мы уже некоторое время назад зашли на территорию полей, просто я вас об этом не предупредил – я хотел сконцентрироваться на волнах, возникающих на этих полях. Описывая то, как ведут себя волны, мы выражали их форму и зависимость от времени при помощи функции Z(x,t). Ну так вот, Z(x,t) – это поле. Это функция пространства и времени с уравнением движения, определяющим её поведение. Подходящей функцией движения была бы такая, что если Z увеличивается или уменьшается в определённой точке, то Z будет уменьшаться или увеличиваться в соседних точках чуть попозже. Эта особенность позволяет волнам оказываться в числе решений уравнения.
В этой статье мы посмотрим на несколько примеров полей Z(x,t), чьи уравнения движения разрешают наличие волн. Физическая интерпретация у этих полей будет самой разной. Они описывают разные свойства разных материалов. Но уравнения, которым они удовлетворяют, и волны, которые они демонстрируют, будут удовлетворять очень похожей математике, и вести они себя тоже будут похоже, несмотря на различное физическое происхождение. Это в будущем станет очень важным моментом.
А затем мы сделаем нечто радикальное – рассмотрим поля в контексте специальной теории относительности. Как показал Эйнштейн, если вы подправите пространство и время и заставите их вести не так, как ожидает большая часть людей, вы получите поле нового типа – такое, что его физическая интерпретация будет не свойством чего-либо ещё, а самостоятельным физическим объектом.
Поле Z(x,t) может представлять множество разных физических величин. К примеру:
• Высоту верёвки, протянутой через комнату.
• Высоту воды в реке.
• Плотность кристалла или газа.
• Положение атомов в магните.
• Скорость ветра.
• Температуру, плотность или давление воздуха.
В любом из этих случаев существует поле Z(x,t): поле высоты, поле плотности, поле ориентации, поле ветра, поле температуры. Его значение в виде функции пространства и времени сообщает нам высоту, плотность, ориентацию, скорость ветра или температуру какой-то среды – верёвки, реки, кристалла, газа, магнита, воздуха – во всех местах в любой момент времени. Его уравнение движения показывает, как себя в принципе может вести Z(x,t). Также оно показывает, как предсказывать поведение Z(x,t) в будущем, если нам точно известно его поведение в настоящем и прошлом.
В каждом примере есть поле и среда, и мы не должны путать поле со средой. Поле просто описывает и характеризует одно из множества свойств соответствующей среды. У совершенно разных сред могут быть очень похоже ведущие себя поля с очень похожими волнами – мы это ещё увидим.
Ещё раз разъясню момент, часто вызывающий непонимание. В общем поле может не иметь ничего общего с физическим расстоянием в пространстве. Да, в статьях 3 и 4 я использовал пример волы на верёвке для иллюстрации того, какой может быть Z(x,t), поскольку это красиво и интуитивно понятно. Также я часто строил графики Z(x,t) для волн. Это может создать у вас ложное впечатление, что Z(x,t) всегда связана с волнами, заставляющими физический объект (типа верёвки) двигаться на расстояние Z в направлении, перпендикулярном оси х. Но это не так, что и продемонстрируют нам три из четырёх наших примеров.
Сначала рассмотрим наш первоначальный пример волн, колеблющуюся верёвку. В данном случае в роли Z(x,t) выступает поле высоты, которое мы назовём H(x,t). Оно сообщает нам высоту верёвки в каждой точке пространства на оси х, идущей вдоль верёвки, в любой момент времени t. Если верёвка находится на равновесной высоте H0, тогда H(x,t) = H0. Поле высоты – константа в пространстве и времени. Если через него движется простая волна, то поле высоты будет описываться нашей знаменитой волновой формулой из предыдущих статей.
Если нам известна H(x,t), мы знаем высоту верёвки во всех точках пространства и времени. Если мы знаем, что верёвка делает сейчас и что она делала совсем недавно, при помощи уравнения движения мы можем предсказать, что она сделает в будущем. Это мало что сообщает нам о самой верёвке. Поле высоты даёт нам только то, что подразумевает его имя: высоту верёвки. Верёвка – это физическая среда, чья высота представлена в виде поля H(x,t); оно ничего не говорит нам о цвете верёвке, её толщине, натяжении, материале и т.п.
На рис. 1 я сделал для вас анимацию волны в поле высоты, идущей слева направо. Может показаться, что я нарисовал одно и то же дважды, сначала зелёным, а затем оранжевым. Но это не одно и то же. Оранжевая кривая – это сама верёвка, двигающаяся в физическом пространстве. Зелёная кривая – это график, представляющий происходящее с H(x,t) безотносительно того, что означает H(x,t) (т.е. высоту), или что это за среда. И только в этом случае зелёный график выглядит точно так же, как происходящее в физическом мире. Но во всех остальных случаях это уже будет не так.

Рис. 1
Допустим, у нас есть среда, состоящая из кристалла с равномерно распределёнными на одинаковых расстояниях друг от друга атомами. Я нарисовал их на рис. 2 в одном измерении – можно представить себе схожие ситуации с тремя измерениями, но пока это было бы ненужным усложнением. Также я отметил каждый 10-й атом красным, чтобы вам легче было отслеживать их движение. И расстояние между атомами я тоже сильно преувеличил – представьте, что между каждыми двумя красными точками находится несколько миллионов атомов, а не 10.
Посмотрим на поле смещения D(x,t), сообщающее нам, насколько в момент времени t атом, обычно находящийся в точке равновесия x, сдвинулся от этой точки в решётке. Это значит, что в случае статичного состояния, с которого начинается анимация, поле везде нулевое, D(x,t) = 0, поскольку все атомы находятся в своей обычной позиции. Затем на анимации отдельные атомы начинают колебаться вперёд-назад, и их движение, в общем и целом, распространяется в виде волны, идущей слева направо. Вверху рисунка график поля смещения решётки D(x,t) показывает, как ведёт себя поле при прохождении волны. Отметим, что поля на рис. 1 и 2 ведут себя схожим образом, при том, что физическая интерпретация полей сильно отличается.

Рис. 2
Что такое постоянный магнит? Он состоит из набора атомов, каждый из которых служит крохотным магнитиком с крохотным магнитным полем, и все они выровнены так, что совместно создают большое магнитное поле. Магнит изображён на рис. 3, и в нём каждый атом направлен вверх. В этом случае поле ориентации ?(x,t) говорит нам насколько далеко в момент времени t атом в точке x отклонился от вертикали. ?, короче говоря, будет углом между магнитиком каждого атома и вертикалью. Анимация на рис. 3 показывает волну в магните, в котором направления атомных магнитов колеблются влево и вправо. Над магнитом зелёным показан график ?(x,t); и снова он выглядит точно так же, как и в предыдущих случаях.

Рассмотрим молекулярный газ в длинной трубе. Вдоль трубы будет расположено измерение х. Молекулы газа будут двигаться почти случайным образом, сталкиваясь со стенками трубы и друг с другом. В равновесии плотность (количество молекул в определённом объёме) и давление P(x,t) (сила, действующая на поверхность небольшого шарика, появившегося в точке х в момент времени t) постоянны. Но звуковые волны, проходящие через газ, заставят давление и плотность колебаться, как показано на рис. 4. Плотность и давление периодически увеличиваются и уменьшаются. Молекулы движутся вперёд и назад, хотя в среднем они вообще не движутся, но при этом волна и её энергия передвигается слева направо по газу. График P(x,t) выглядит опять-таки очень похоже на предыдущие.
Что мы можем извлечь из четырёх примеров, показывающих волны класса 0? (У уравнения движения есть одна величина, cw, и все волны в соответствующем поле перемещаются со скоростью cw. У разных полей класса 0 будут разные значения cw). Мы можем узнать, что одинаковое поведение поля может появиться из физически различных полей, существующих у физически различных сред. Несмотря на разное происхождение, волны в поле высоты, в поле смещения решётки, в поле магнитной ориентации и в поле давления газа выглядят идентично с точки зрения полей. Они удовлетворяют одному и тому же типу уравнения движения и одному и тому же численному взаимоотношению частоты и длины волны.
Мелкий шрифт: строго говоря, если вы создадите волны достаточно небольшой длины, вы всё же сможете различить поведение различных сред. Как только длины волн сравняются с расстоянием между атомами верёвки, или кристалла, или магнита, волновые уравнения, которым будут удовлетворять волны, окажутся более сложными, чем записанные нами, и их детали позволят отличить среды друг от друга. Но часто в практических экспериментах мы даже близко не подходим к наблюдению подобных эффектов.
Результатом этого будет то, что изучение волн и их квантов, связанное с полями, не обязательно сообщит вам о том, что служит в качестве среды, или какова физическая интерпретация поля – какое из свойств среды оно представляет. И даже, если вы каким-то образом знаете, что это поле определённого типа – допустим, поле давления – вы обычно всё равно не сможете сказать, исходя из его поведения, давление чего именно оно представляет. Всё, что вы можете узнать, изучая волны – принадлежит ли поле к классу 0 или классу 1, и какова у него величина cw; или же узнать, что поле принадлежит к другому классу.
В каких-то случаях это очень плохо; поле передаёт только частичную информацию о среде. Иногда это довольно удобно; поле — более абстрактная и универсальная штука, чем описываемый им физический материал.
Поэтому поле не определяет среду, а его поведение часто не зависит от подробностей и свойств среды. Из-за чего возникает вопрос.
Может ли существовать физическое поле – с волнами, состоящими из квантов, движущихся в пространстве и переносящих энергию – безо всякой поддерживающей его среды?
Песню без певца не услышишь. Но у песни есть какого-то рода независимое существование; она звучит по-разному, в зависимости от того, кто её поёт, но при этом в песне есть что-то неотъемлемое, какое-то абстрактное качество, благодаря которому её всегда можно узнать. Эта абстрактная сущность – мелодия песни. Мы можем обсуждать, изучать, выучить мелодию, записать её при помощи музыкальной записи, даже не услышав её в исполнении певца. Многие из нас даже могут напевать её про себя в голове. Каким-то образом мелодия существует даже если никто не исполняет песню.
Если во всех данных мною примерах и во всех примерах, которые я могу дать, и которые будут интуитивно понятны вам, поле описывает свойство среди, тогда как может существовать поле без среды? Но каким-то образом поля не зависят от своей среды, поскольку множество различных полей могут вести себя одинаково, несмотря на то, что они описывают множество различных свойств совершенно отличных сред. Так что, вероятно, возможно абстрагировать поле от среды.
На самом деле, это не только возможно, это, судя по всему, и необходимо. По меньшей мере, необходимо либо не иметь никакой среды, или же иметь среду, которую невозможно создать из обычной материи, которая кардинально отличается от всех рассмотренных нами сред – в том, что она функционирует так (согласно всем проведённым экспериментам), будто её вообще нет.
Одним из нескольких радикальных элементов специальной теории относительности Эйнштейна от 1905 года была идея, что для световых волн – десятилетиями считавшихся волнами в электрическом и магнитном полях (электромагнитных волн), и перемещающихся с одинаковой скоростью в пустом пространстве – никакой среды нет. Есть только поля.
Гипотетическую среду называли «эфиром»; Эйнштейн утверждал, что такой вещи не существует, и записал набор уравнений, для которых её не требовалось. Отмечу, что всё ещё идут дебаты (часто более философские, чем физические) по поводу того, нужно или не нужно представлять себе существование какой-то странной среды, сильно отличающейся от обычной материи. На сегодняшний день нет свидетельств, требующих её наличия.
Ключевыми элементами эйнштейновской версии относительности (в отличие от версий Галилея и Ньютона) были следующие:
• Пространство и время не такие, какими вы их считаете. Разные наблюдатели, равномерно движущиеся друг относительно друга, разойдутся в своих оценках длины объектов и временных промежутках между событиями (и эти расхождения можно точно измерить).
• Существует универсальный лимит скорости, с; любой наблюдатель, измеряющий скорость объекта по отношению к нему, найдёт, что эта скорость меньше или равна с.
• В таком мире определённые поля – «релятивистские поля» – могут существовать без среды, и они удовлетворяют специальным уравнениям движения. Простейшее релятивистское поле удовлетворяет уравнениям движения классов 0 или 1, со скоростью волны cw, упомянутой в уравнении движения, принимающей значение с.
Короче говоря, существуют релятивистские поля класса 0, удовлетворяющие уравнению
Свет, и все электромагнитные волны, представляет собой самый известный, но не уникальный пример – поэтому «с» часто называют «скоростью света». И существуют релятивистские поля класса 1, удовлетворяющие уравнению
Их примеры мы увидим в следующей статье. Отметьте, что относительность не налагает ограничений на ? (кроме необходимости, чтобы ?2 было положительным) или на Z0. Для релятивистских полей существуют и более сложные уравнения, но большинство из них в описании простых физических процессов сводятся к одному из этих двух.
Релятивистские поля физически реальны и имеют физический смысл во Вселенной, то бишь:
• Их волны переносят энергию и информацию из одного места в другое.
• Волны в одном поле могут влиять на другое поле и менять физические процессы, которые проходили бы в их отсутствие.
Но, в отличие от полей, примеры которых даны в этой статье, релятивистские поля не описывают свойство какой-либо обычной физической среды, состоящей из чего-либо, напоминающего обычную материю, и, насколько это экспериментально известно, они не описывают свойства вообще чего бы то ни было. Эти поля, возможно, насколько нам сегодня известно, являются одним из фундаментальных элементов Вселенной.
2) квантовый шар на пружине
3) волны, классический вид
4) волны, классическое уравнение движения
5) квантовые волны
6) поля
На самом деле мы уже некоторое время назад зашли на территорию полей, просто я вас об этом не предупредил – я хотел сконцентрироваться на волнах, возникающих на этих полях. Описывая то, как ведут себя волны, мы выражали их форму и зависимость от времени при помощи функции Z(x,t). Ну так вот, Z(x,t) – это поле. Это функция пространства и времени с уравнением движения, определяющим её поведение. Подходящей функцией движения была бы такая, что если Z увеличивается или уменьшается в определённой точке, то Z будет уменьшаться или увеличиваться в соседних точках чуть попозже. Эта особенность позволяет волнам оказываться в числе решений уравнения.
В этой статье мы посмотрим на несколько примеров полей Z(x,t), чьи уравнения движения разрешают наличие волн. Физическая интерпретация у этих полей будет самой разной. Они описывают разные свойства разных материалов. Но уравнения, которым они удовлетворяют, и волны, которые они демонстрируют, будут удовлетворять очень похожей математике, и вести они себя тоже будут похоже, несмотря на различное физическое происхождение. Это в будущем станет очень важным моментом.
А затем мы сделаем нечто радикальное – рассмотрим поля в контексте специальной теории относительности. Как показал Эйнштейн, если вы подправите пространство и время и заставите их вести не так, как ожидает большая часть людей, вы получите поле нового типа – такое, что его физическая интерпретация будет не свойством чего-либо ещё, а самостоятельным физическим объектом.
Обычные поля, описывающие обычные вещи
Поле Z(x,t) может представлять множество разных физических величин. К примеру:
• Высоту верёвки, протянутой через комнату.
• Высоту воды в реке.
• Плотность кристалла или газа.
• Положение атомов в магните.
• Скорость ветра.
• Температуру, плотность или давление воздуха.
В любом из этих случаев существует поле Z(x,t): поле высоты, поле плотности, поле ориентации, поле ветра, поле температуры. Его значение в виде функции пространства и времени сообщает нам высоту, плотность, ориентацию, скорость ветра или температуру какой-то среды – верёвки, реки, кристалла, газа, магнита, воздуха – во всех местах в любой момент времени. Его уравнение движения показывает, как себя в принципе может вести Z(x,t). Также оно показывает, как предсказывать поведение Z(x,t) в будущем, если нам точно известно его поведение в настоящем и прошлом.
В каждом примере есть поле и среда, и мы не должны путать поле со средой. Поле просто описывает и характеризует одно из множества свойств соответствующей среды. У совершенно разных сред могут быть очень похоже ведущие себя поля с очень похожими волнами – мы это ещё увидим.
Ещё раз разъясню момент, часто вызывающий непонимание. В общем поле может не иметь ничего общего с физическим расстоянием в пространстве. Да, в статьях 3 и 4 я использовал пример волы на верёвке для иллюстрации того, какой может быть Z(x,t), поскольку это красиво и интуитивно понятно. Также я часто строил графики Z(x,t) для волн. Это может создать у вас ложное впечатление, что Z(x,t) всегда связана с волнами, заставляющими физический объект (типа верёвки) двигаться на расстояние Z в направлении, перпендикулярном оси х. Но это не так, что и продемонстрируют нам три из четырёх наших примеров.
Поле высоты верёвки
Сначала рассмотрим наш первоначальный пример волн, колеблющуюся верёвку. В данном случае в роли Z(x,t) выступает поле высоты, которое мы назовём H(x,t). Оно сообщает нам высоту верёвки в каждой точке пространства на оси х, идущей вдоль верёвки, в любой момент времени t. Если верёвка находится на равновесной высоте H0, тогда H(x,t) = H0. Поле высоты – константа в пространстве и времени. Если через него движется простая волна, то поле высоты будет описываться нашей знаменитой волновой формулой из предыдущих статей.
Если нам известна H(x,t), мы знаем высоту верёвки во всех точках пространства и времени. Если мы знаем, что верёвка делает сейчас и что она делала совсем недавно, при помощи уравнения движения мы можем предсказать, что она сделает в будущем. Это мало что сообщает нам о самой верёвке. Поле высоты даёт нам только то, что подразумевает его имя: высоту верёвки. Верёвка – это физическая среда, чья высота представлена в виде поля H(x,t); оно ничего не говорит нам о цвете верёвке, её толщине, натяжении, материале и т.п.
На рис. 1 я сделал для вас анимацию волны в поле высоты, идущей слева направо. Может показаться, что я нарисовал одно и то же дважды, сначала зелёным, а затем оранжевым. Но это не одно и то же. Оранжевая кривая – это сама верёвка, двигающаяся в физическом пространстве. Зелёная кривая – это график, представляющий происходящее с H(x,t) безотносительно того, что означает H(x,t) (т.е. высоту), или что это за среда. И только в этом случае зелёный график выглядит точно так же, как происходящее в физическом мире. Но во всех остальных случаях это уже будет не так.

Рис. 1
Поле смещения решётки
Допустим, у нас есть среда, состоящая из кристалла с равномерно распределёнными на одинаковых расстояниях друг от друга атомами. Я нарисовал их на рис. 2 в одном измерении – можно представить себе схожие ситуации с тремя измерениями, но пока это было бы ненужным усложнением. Также я отметил каждый 10-й атом красным, чтобы вам легче было отслеживать их движение. И расстояние между атомами я тоже сильно преувеличил – представьте, что между каждыми двумя красными точками находится несколько миллионов атомов, а не 10.
Посмотрим на поле смещения D(x,t), сообщающее нам, насколько в момент времени t атом, обычно находящийся в точке равновесия x, сдвинулся от этой точки в решётке. Это значит, что в случае статичного состояния, с которого начинается анимация, поле везде нулевое, D(x,t) = 0, поскольку все атомы находятся в своей обычной позиции. Затем на анимации отдельные атомы начинают колебаться вперёд-назад, и их движение, в общем и целом, распространяется в виде волны, идущей слева направо. Вверху рисунка график поля смещения решётки D(x,t) показывает, как ведёт себя поле при прохождении волны. Отметим, что поля на рис. 1 и 2 ведут себя схожим образом, при том, что физическая интерпретация полей сильно отличается.

Рис. 2
Поле магнитной ориентации
Что такое постоянный магнит? Он состоит из набора атомов, каждый из которых служит крохотным магнитиком с крохотным магнитным полем, и все они выровнены так, что совместно создают большое магнитное поле. Магнит изображён на рис. 3, и в нём каждый атом направлен вверх. В этом случае поле ориентации ?(x,t) говорит нам насколько далеко в момент времени t атом в точке x отклонился от вертикали. ?, короче говоря, будет углом между магнитиком каждого атома и вертикалью. Анимация на рис. 3 показывает волну в магните, в котором направления атомных магнитов колеблются влево и вправо. Над магнитом зелёным показан график ?(x,t); и снова он выглядит точно так же, как и в предыдущих случаях.

Поле давления воздуха
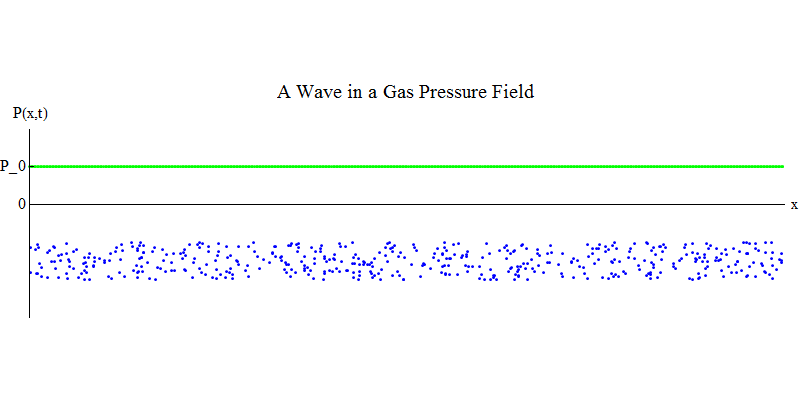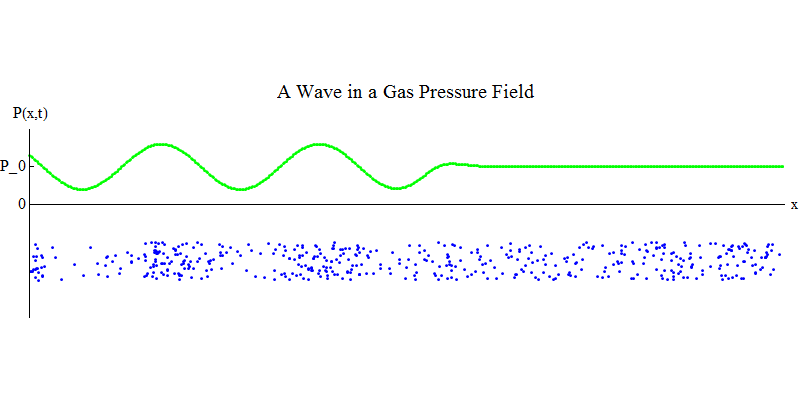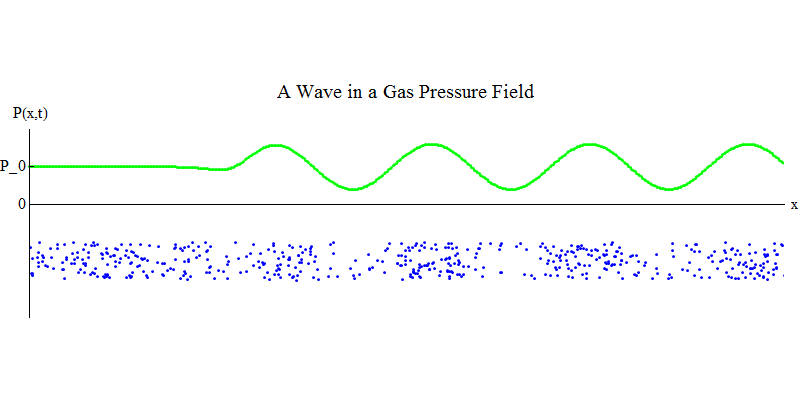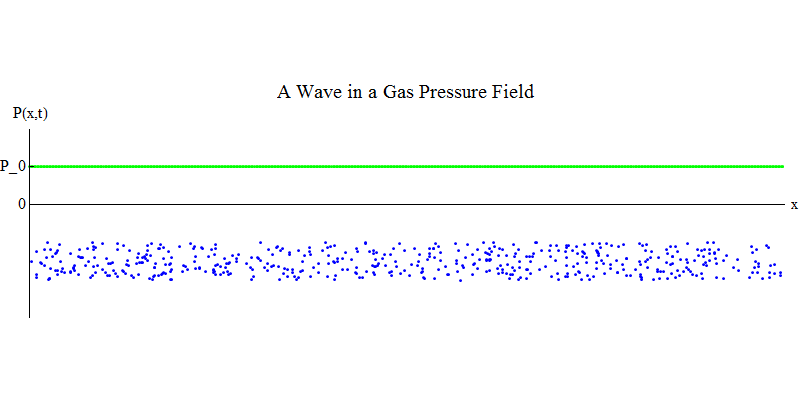
Рассмотрим молекулярный газ в длинной трубе. Вдоль трубы будет расположено измерение х. Молекулы газа будут двигаться почти случайным образом, сталкиваясь со стенками трубы и друг с другом. В равновесии плотность (количество молекул в определённом объёме) и давление P(x,t) (сила, действующая на поверхность небольшого шарика, появившегося в точке х в момент времени t) постоянны. Но звуковые волны, проходящие через газ, заставят давление и плотность колебаться, как показано на рис. 4. Плотность и давление периодически увеличиваются и уменьшаются. Молекулы движутся вперёд и назад, хотя в среднем они вообще не движутся, но при этом волна и её энергия передвигается слева направо по газу. График P(x,t) выглядит опять-таки очень похоже на предыдущие.

Важные уроки
Что мы можем извлечь из четырёх примеров, показывающих волны класса 0? (У уравнения движения есть одна величина, cw, и все волны в соответствующем поле перемещаются со скоростью cw. У разных полей класса 0 будут разные значения cw). Мы можем узнать, что одинаковое поведение поля может появиться из физически различных полей, существующих у физически различных сред. Несмотря на разное происхождение, волны в поле высоты, в поле смещения решётки, в поле магнитной ориентации и в поле давления газа выглядят идентично с точки зрения полей. Они удовлетворяют одному и тому же типу уравнения движения и одному и тому же численному взаимоотношению частоты и длины волны.
Мелкий шрифт: строго говоря, если вы создадите волны достаточно небольшой длины, вы всё же сможете различить поведение различных сред. Как только длины волн сравняются с расстоянием между атомами верёвки, или кристалла, или магнита, волновые уравнения, которым будут удовлетворять волны, окажутся более сложными, чем записанные нами, и их детали позволят отличить среды друг от друга. Но часто в практических экспериментах мы даже близко не подходим к наблюдению подобных эффектов.
Результатом этого будет то, что изучение волн и их квантов, связанное с полями, не обязательно сообщит вам о том, что служит в качестве среды, или какова физическая интерпретация поля – какое из свойств среды оно представляет. И даже, если вы каким-то образом знаете, что это поле определённого типа – допустим, поле давления – вы обычно всё равно не сможете сказать, исходя из его поведения, давление чего именно оно представляет. Всё, что вы можете узнать, изучая волны – принадлежит ли поле к классу 0 или классу 1, и какова у него величина cw; или же узнать, что поле принадлежит к другому классу.
В каких-то случаях это очень плохо; поле передаёт только частичную информацию о среде. Иногда это довольно удобно; поле — более абстрактная и универсальная штука, чем описываемый им физический материал.
Поэтому поле не определяет среду, а его поведение часто не зависит от подробностей и свойств среды. Из-за чего возникает вопрос.
Может ли существовать физическое поле – с волнами, состоящими из квантов, движущихся в пространстве и переносящих энергию – безо всякой поддерживающей его среды?
Поле без среды?
Песню без певца не услышишь. Но у песни есть какого-то рода независимое существование; она звучит по-разному, в зависимости от того, кто её поёт, но при этом в песне есть что-то неотъемлемое, какое-то абстрактное качество, благодаря которому её всегда можно узнать. Эта абстрактная сущность – мелодия песни. Мы можем обсуждать, изучать, выучить мелодию, записать её при помощи музыкальной записи, даже не услышав её в исполнении певца. Многие из нас даже могут напевать её про себя в голове. Каким-то образом мелодия существует даже если никто не исполняет песню.
Если во всех данных мною примерах и во всех примерах, которые я могу дать, и которые будут интуитивно понятны вам, поле описывает свойство среди, тогда как может существовать поле без среды? Но каким-то образом поля не зависят от своей среды, поскольку множество различных полей могут вести себя одинаково, несмотря на то, что они описывают множество различных свойств совершенно отличных сред. Так что, вероятно, возможно абстрагировать поле от среды.
На самом деле, это не только возможно, это, судя по всему, и необходимо. По меньшей мере, необходимо либо не иметь никакой среды, или же иметь среду, которую невозможно создать из обычной материи, которая кардинально отличается от всех рассмотренных нами сред – в том, что она функционирует так (согласно всем проведённым экспериментам), будто её вообще нет.
Одним из нескольких радикальных элементов специальной теории относительности Эйнштейна от 1905 года была идея, что для световых волн – десятилетиями считавшихся волнами в электрическом и магнитном полях (электромагнитных волн), и перемещающихся с одинаковой скоростью в пустом пространстве – никакой среды нет. Есть только поля.
Гипотетическую среду называли «эфиром»; Эйнштейн утверждал, что такой вещи не существует, и записал набор уравнений, для которых её не требовалось. Отмечу, что всё ещё идут дебаты (часто более философские, чем физические) по поводу того, нужно или не нужно представлять себе существование какой-то странной среды, сильно отличающейся от обычной материи. На сегодняшний день нет свидетельств, требующих её наличия.
Ключевыми элементами эйнштейновской версии относительности (в отличие от версий Галилея и Ньютона) были следующие:
• Пространство и время не такие, какими вы их считаете. Разные наблюдатели, равномерно движущиеся друг относительно друга, разойдутся в своих оценках длины объектов и временных промежутках между событиями (и эти расхождения можно точно измерить).
• Существует универсальный лимит скорости, с; любой наблюдатель, измеряющий скорость объекта по отношению к нему, найдёт, что эта скорость меньше или равна с.
• В таком мире определённые поля – «релятивистские поля» – могут существовать без среды, и они удовлетворяют специальным уравнениям движения. Простейшее релятивистское поле удовлетворяет уравнениям движения классов 0 или 1, со скоростью волны cw, упомянутой в уравнении движения, принимающей значение с.
Короче говоря, существуют релятивистские поля класса 0, удовлетворяющие уравнению
Свет, и все электромагнитные волны, представляет собой самый известный, но не уникальный пример – поэтому «с» часто называют «скоростью света». И существуют релятивистские поля класса 1, удовлетворяющие уравнению
Их примеры мы увидим в следующей статье. Отметьте, что относительность не налагает ограничений на ? (кроме необходимости, чтобы ?2 было положительным) или на Z0. Для релятивистских полей существуют и более сложные уравнения, но большинство из них в описании простых физических процессов сводятся к одному из этих двух.
Релятивистские поля физически реальны и имеют физический смысл во Вселенной, то бишь:
• Их волны переносят энергию и информацию из одного места в другое.
• Волны в одном поле могут влиять на другое поле и менять физические процессы, которые проходили бы в их отсутствие.
Но, в отличие от полей, примеры которых даны в этой статье, релятивистские поля не описывают свойство какой-либо обычной физической среды, состоящей из чего-либо, напоминающего обычную материю, и, насколько это экспериментально известно, они не описывают свойства вообще чего бы то ни было. Эти поля, возможно, насколько нам сегодня известно, являются одним из фундаментальных элементов Вселенной.

