В одной из мозаик Пенроуза используются всего два ромба, отличающиеся углами. Из этих элементов можно выстроить апериодическую мозайку любых размеров. Для её отображения я попробовал представить координаты аналитически.


Распределение углов в ромбах в одном 1:4, 36°:144°, в другом 2:3, 72°:108°. Углы в ромбах кратны одной десятой полного разворота, 36°.

Определим координаты углов правильного десятиугольника.

градус	cos	sin
0	1	0
36	0,809017	0,587785
72	0,309017	0,951056

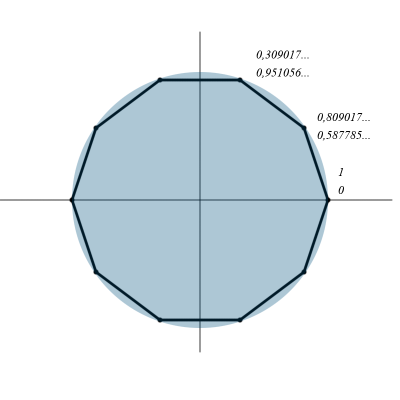
Остальные симметрично, меняется только знак.

Сразу заметно, что косинусы углов 36° и 72° отличаются на 0,5. И это очень многозначительный факт!

Абсолютных значений координат ровно три штуки — и для координат абсциссных и для ординатных. Все три могут быть представлены как два коэффициента с целыми множителями.

Для абсциссных координат это просто: среди значений ноль, который представлен нулевыми множителями. Среди ординатных координат третья — единица — не соразмерна остальным двум. Но, так как разница координат это 0,5, то эта разница может стать одним из коэффициентов, а второй коэффициент будет меньшим значением. Значение 1 получится множителем 2.

*36°	x		y
	Cxa=0,5	Cxb=0,309017	Cya=0,951056	Cxb=0,587785
0	2	0	0	0
1	1	1	0	1
2	0	1	1	0
3	0	-1	1	0
4	-1	-1	0	1
5	-2	0	0	0
6	-1	-1	0	-1
7	0	-1	-1	0
8	0	1	-1	0
9	1	1	0	-1

И значит, существует целочисленная система координат.

$$


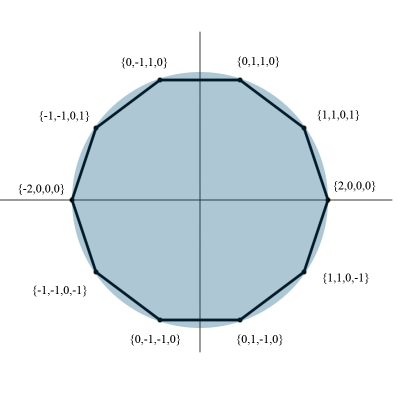
Коэффициенты попарно различаются на один и тот же множитель, это коэффициент золотого сечения.

$$

$$

$$

Можно вывести точное представление для коэффициентов.

$$

$$

$$

$$

Дальше магия золотого сечения:

$$

$$

$$

$$

Отсюда множество закономерностей:

Тривиальные:

$$
$$
$$
$$

Из-за равенства отношения коэффициентов:

$$
$$

Квадраты коэффициентов:

$$
$$
$$

Произведение:

$$

Исходя из этих свойств можно составить матрицу для целочисленного умножения векторов:

const crd vmul[16] = {
{ 1, 0, 0, 0}, { 0, 1, 0, 0}, { 0, 0, 1, 0}, { 0, 0, 0, 1}, 
{ 0, 1, 0, 0}, { 1,-1, 0, 0}, { 0, 0, 0, 1}, { 0, 0, 1,-1}, 
{ 0, 0, 1, 0}, { 0, 0, 0, 1}, {-3,-1, 0, 0}, {-1,-2, 0, 0}, 
{ 0, 0, 0, 1}, { 0, 0, 1,-1}, {-1,-2, 0, 0}, {-2, 1, 0, 0}
};

И всё перемножение сведётся к

int* vm = (int*)vmul;
for(int i = 0; i < 4; i++) 
  for(int j = 0; j < 4; j++) 
    for(int k = 0; k < 4; k++)
      v3[k] += v1[i] * v2[j] * vm[(i * 4 + j) * 4 + k];

Векторная единица в этой системе выражается как {2,0,0,0}. После простого переменожения таких единиц мы получим {4,0,0,0}. Так что, деление на два, которое было в каждой формуле для коэффициентов, производится отдельно, как нормировка:

for(int i = 0; i < 4; i++) v3[i] /= 2;

Особенность этой координатной системы в том, что она покрывает всю плоскость с любой заданной точностью. Можно повторять любое количество шагов, выбирая любое из десяти направлений и всё равно оставаться в целочисленных координатах.

Но не все сочетания координат определяют место, достижимое из начального положения.

Для одного шага разложения по координатам следующие: {2,0,0,0}, {1,1,0,1}, {0,1,1,0}, {0,-1,1,0}, {-1,-1,0,1}, {-2,0,0,0}, {-1,-1,0,-1}, {0,-1,-1,0}, {0,1,-1,0}, {1,1,0,-1}. Любая комбинация этих шагов допустима.

Вместе с единичным шагом {2,0,0,0} сочетания
{0,1,1,0} – {0,1,-1,0} = {0,0,2,0},
{1,1,0,1} – {1,1,0,-1} = {0,0,0,2},
{1,1,0,1} + {1,1,0,-1} – {2,0,0,0} = {0,2,0,0}
означают, что любую отдельную координату можно сдвинуть на 2, и значит, на достижимость влияет только групповая четность координат. Достижимых сочетаний получается четыре: нулевая: {0,0,0,0}, от одиночных шагов: {1,1,0,1}, {0,1,1,0}, и их комбинация: {1,0,1,1}.

Как видно, групповая четность абциссных координат однозначно взаимосвязана c групповой четностью ординатных координат. Это значит, что вертикальные координаты делятся на четыре типа, горизонтальные координаты тоже делятся на 4 типа, а к координатной системе принадлежат точки исключительно при их правильной комбинации.



Для приближения к произвольной точке нужно разложить каждую координату на подходящие целые множители, учитывая при этом групповую четность.

В общем, существует система координат, которая совмещает целое значение координат и повороты в 36°. Когда я её вывел, был удивлён, что не знал о ней раньше. Но теперь о ней есть статья на Хабре.

$$

$$