Содержание:

Последовательность Фибоначчи O (n)
Решение за O(n ^ 2)
Бинарный поиск O(log n)
Решение за O(n * log n)

Задача

"Найти длину самой большой возрастающей подпоследовательности в массиве."

Вообще, это частный случай задачи нахождения общих элементов 2-х последовательностей, где второй последовательностью является та же самая последовательность, только отсортированная.

На пальцах

Есть последовательность:

5, 10, 6, 12, 3, 24, 7, 8

Вот примеры подпоследовательностей:

10, 3, 8
5, 6, 3

А вот примеры возрастающих подпоследовательностей:

5, 6, 7, 8
3, 7, 8

А вот примеры возрастающих подпоследовательностей наибольшей длины:

5, 6, 12, 24
5, 6, 7, 8

Да, максимальных тоже может быть много, нас интересует лишь длина.
Здесь она равна 4.

Теперь когда задача определена, решать мы ее начинаем с (сюрприз!) вычисления чисел Фибоначчи, ибо вычисление их — это самый простой алгоритм, в котором используется “динамическое программирование”. ДП — термин, который лично у меня никаких правильных ассоциаций не вызывает, я бы назвал этот подход так — “Программирование с сохранением промежуточного результата этой же задачи, но меньшей размерности”. Если же посчитать числа Фибоначчи с помощью ДП для вас проще пареной репы — смело переходите к следующей части. Сами числа Фибоначчи не имеют отношения к исходной задаче о подпоследовательностях, я просто хочу показать принцип ДП.

Последовательность Фибоначчи O(n)

Последовательность Фибоначчи популярна и окружена легендами, разглядеть ее пытаются (и надо признать, им это удается) везде, где только можно. Принцип же ее прост. n-ый элемент последовательности равен сумме n-1 и n-2 элемента. Начинается соответственно с 0 и 1.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34 …

Берем 0, прибавляем 1 — получаем 1.
Берем 1, прибавляем 1 — получаем 2.
Берем 1, прибавляем 2 — получаем, ну вы поняли, 3.

Собственно нахождение n-го элемента этой последовательности и будет нашей задачей. Решение кроется в самом определении этой последовательности. Мы заведем один мутабельный массив, в который будем сохранять промежуточные результаты вычисления чисел Фибоначчи, т.е. те самые n-1 и n-2.

Псевдокод:

int numberForIndex(int index) {

   int[] numbers = [0, 1]; // мутабельный массив, можем добавлять к нему элементы

    for (int i = 2; i < index + 1; i++) {
        numbers[index] = numbers[i - 1] + numbers[i - 2];
    }

    return numbers[index];
}

> Пример решения на Objective-C

> Тесты

Вот и всё, в этом массиве numbers вся соль ДП, это своего рода кэш (Caсhe), в который мы складываем предыдущие результаты вычисления этой же задачи, только на меньшей размерности (n-1 и n-2), что дает нам возможность за одно действие найти решение для размерности n.

Этот алгоритм работает за O(n), но использует немного дополнительной памяти — наш массив.

Вернемся к нахождению длины максимальной возрастающей подпоследовательности.

Решение за O( n ^ 2)

Рассмотрим следующую возрастающую подпоследовательность:

5, 6, 12

теперь взглянем на следующее число после последнего элемента в последовательности — это 3.

Может ли оно быть продолжением нашей последовательности? Нет. Оно меньше чем 12.

А 24 ?

Оно да, оно может.

Соответственно длина нашей последовательности равна теперь 3 + 1, а последовательность выглядит так:

5, 6, 12, 24

Вот где переиспользование предыдущих вычислений: мы знаем что у нас есть подпоследовательность 5, 6, 12, которая имеет длину 3 и теперь нам легко добавить к ней 24. Теперь у вас есть ощущение того, что мы можем это использовать, только как?

Давайте заведем еще один дополнительный массив (вот он наш cache, вот оно наше ДП), в котором будем хранить размер возрастающей подпоследовательности для n-го элемента.

Выглядеть это будет так:

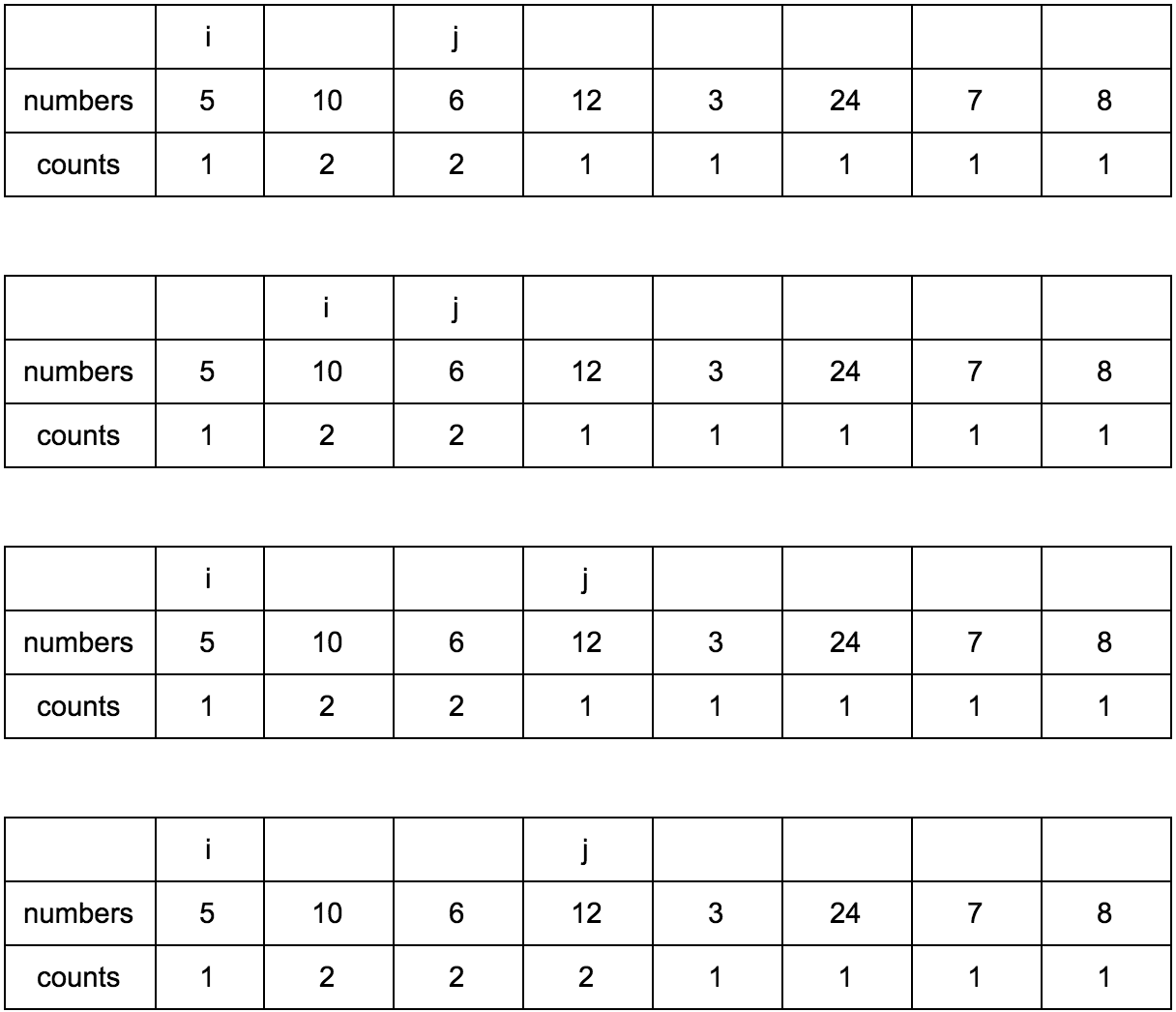
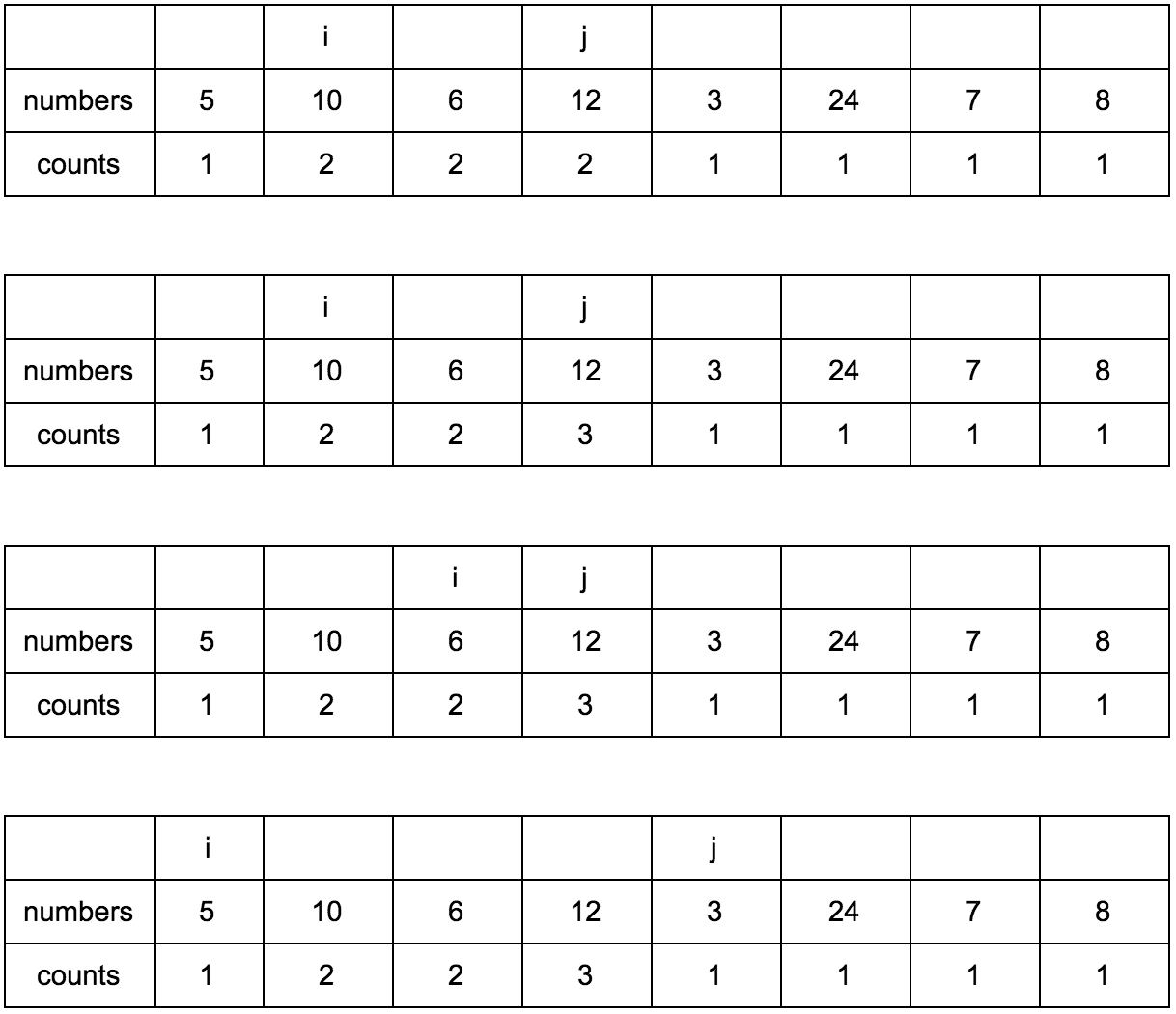
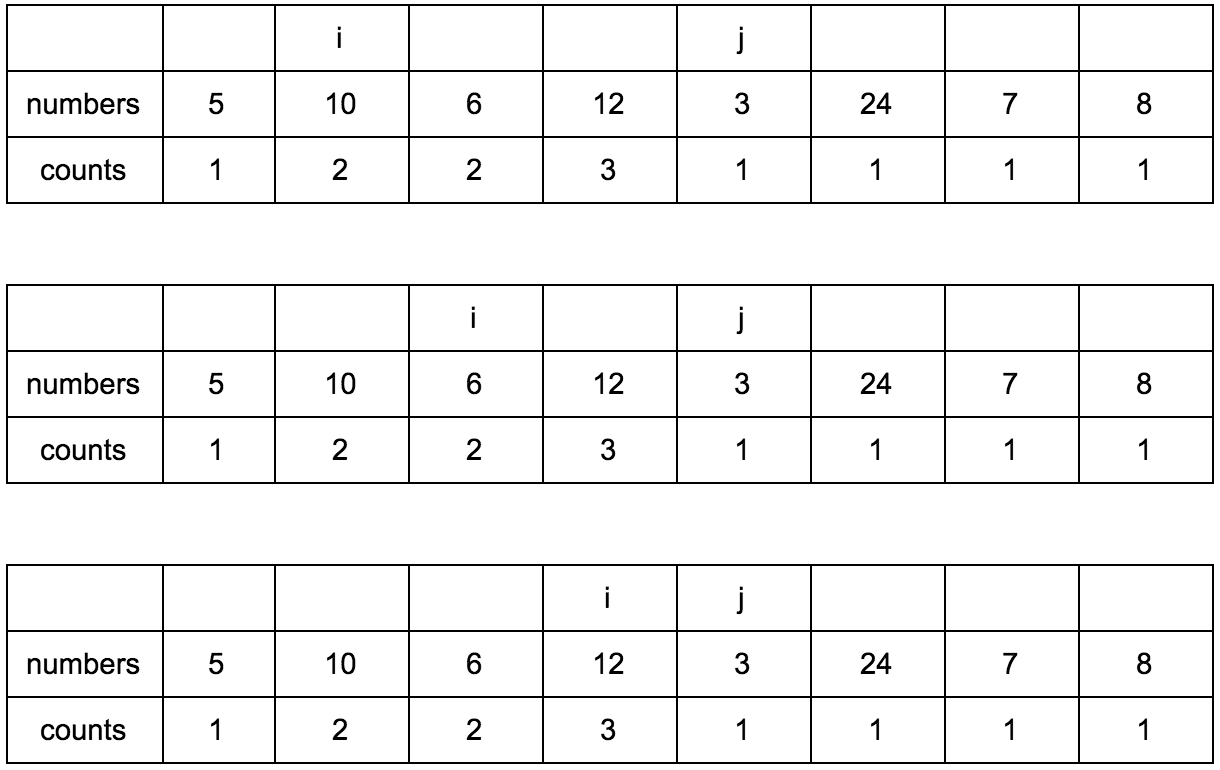
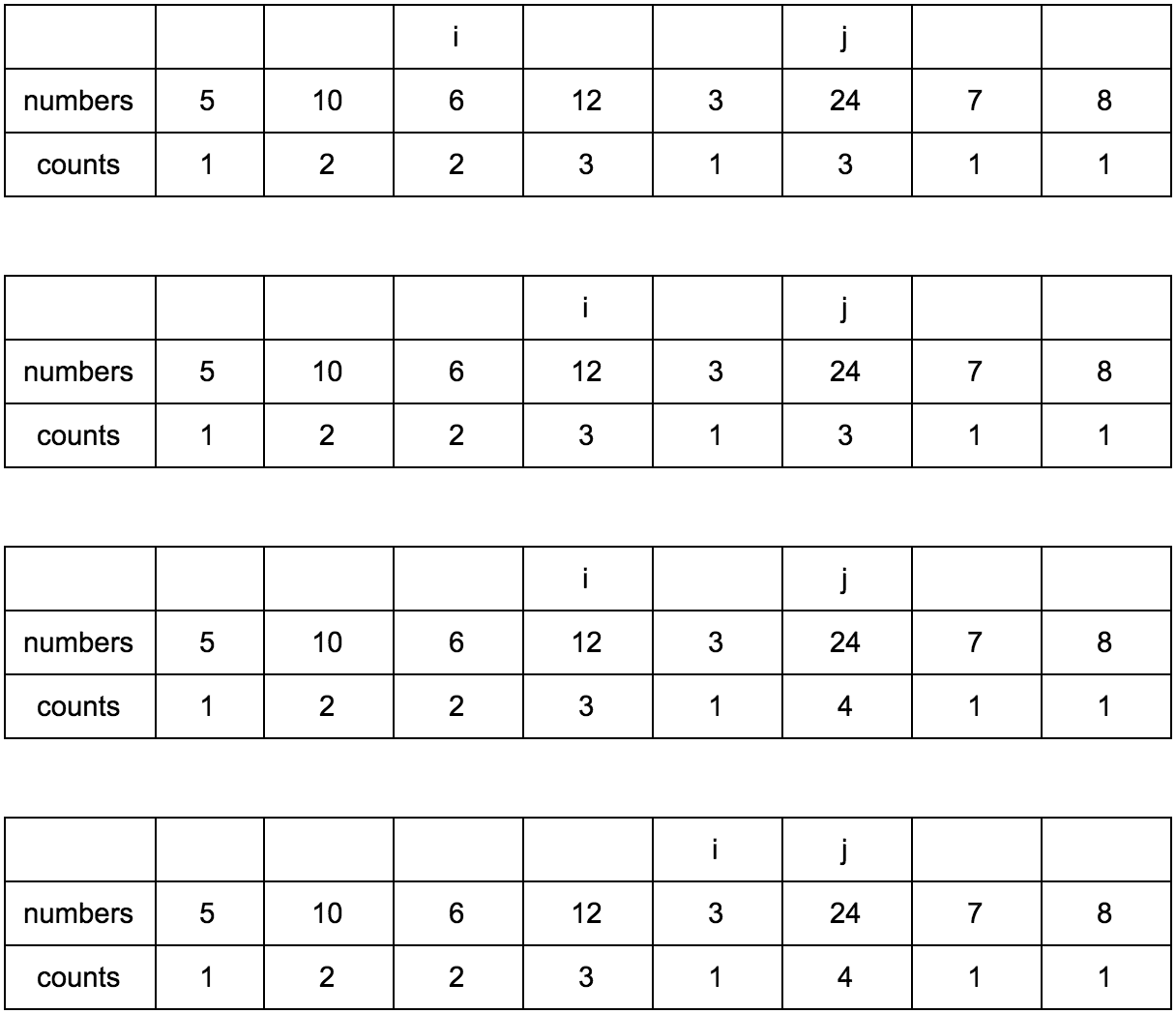
Наша задача — заполнить массив counts правильными значениями. Изначально он заполнен единицами, так как каждый элемент сам по себе является минимальной возрастающей подпоследовательностью.

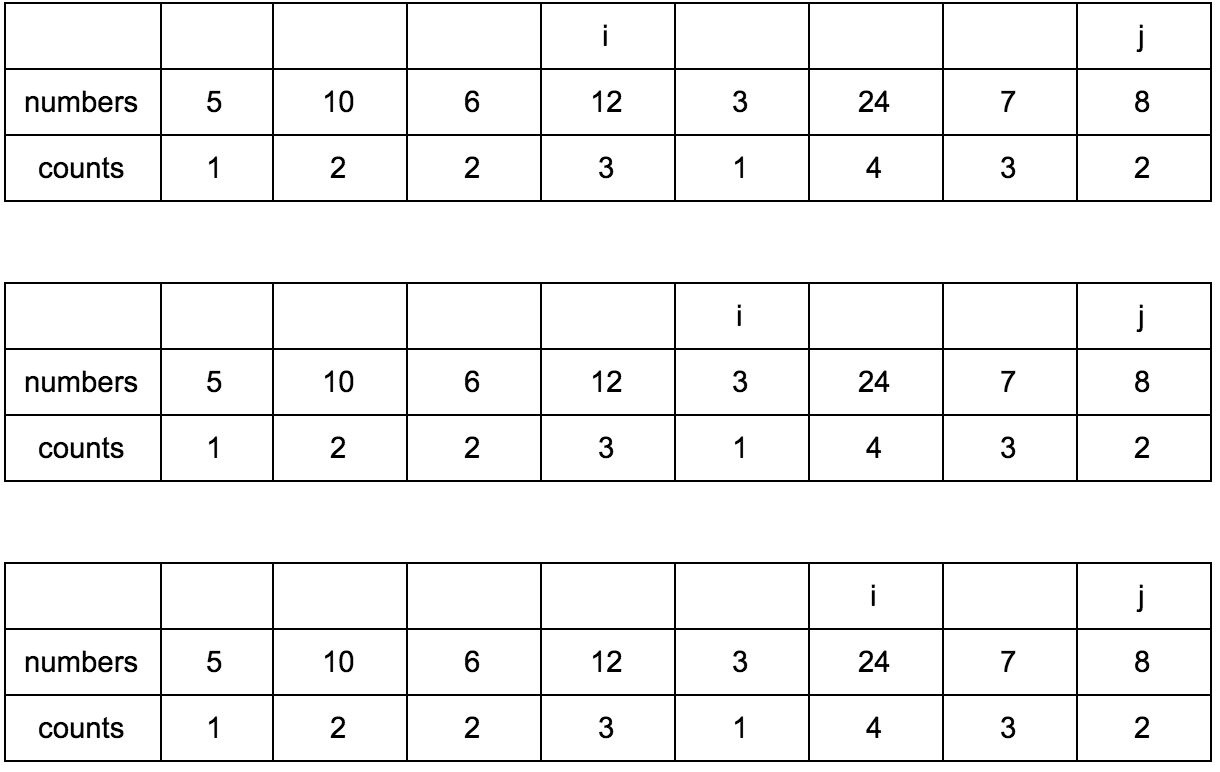
“Что за загадочные i и j?” — спросите вы. Это индексы итераторов по массиву, которые мы будем использовать. Изменяться они будут с помощью двух циклов, один в другом. i всегда будет меньше чем j.

Сейчас j смотрит на 10 — это наш кандидат в члены последовательностей, которые идут до него. Посмотрим туда, где i, там стоит 5.

10 больше 5 и 1 <= 1, counts[j] <= counts[i]? Да, значит counts[j] = counts[i] + 1, помните наши рассуждения в начале?

Теперь таблица выглядит так.

Смещаем j.

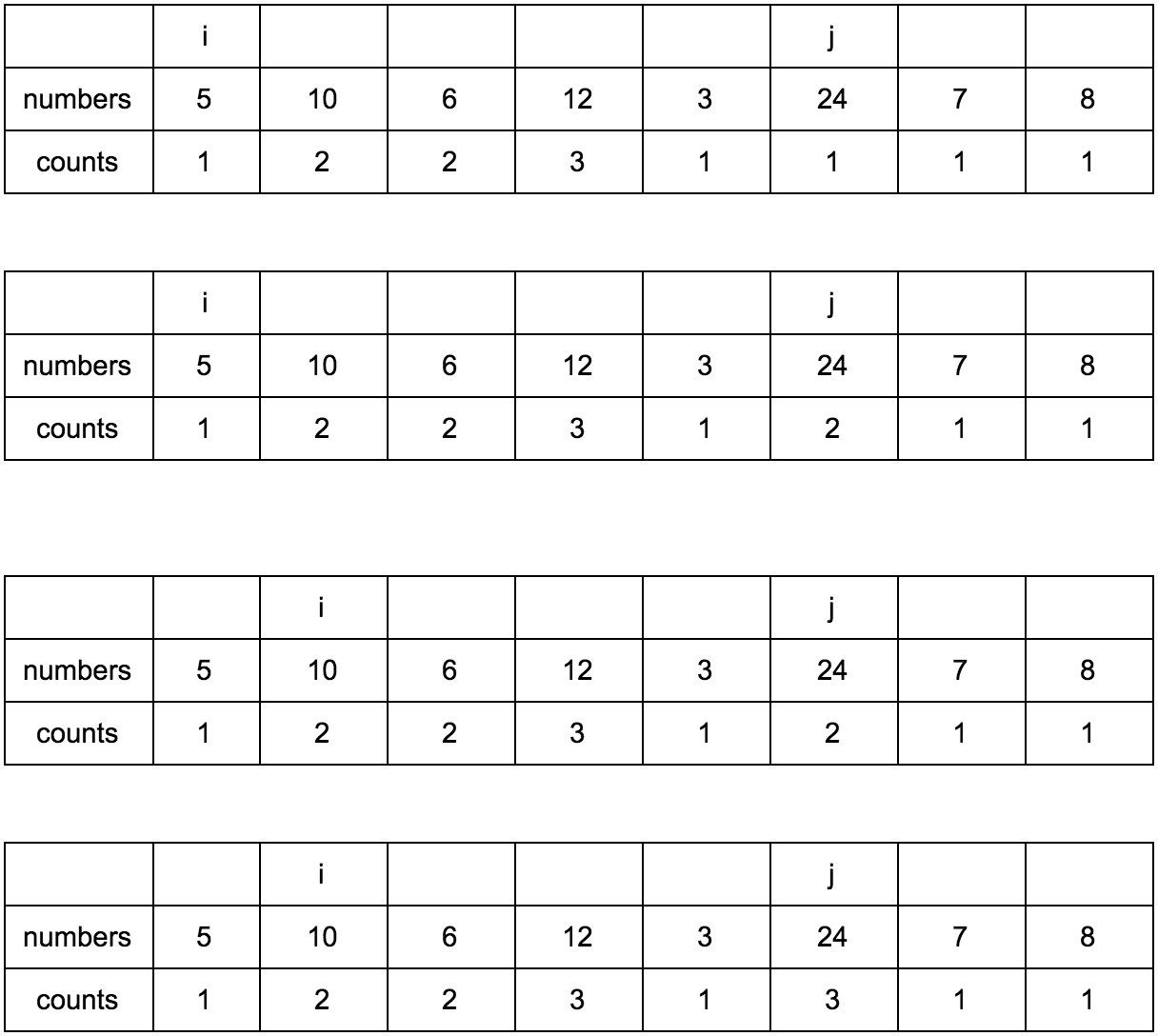
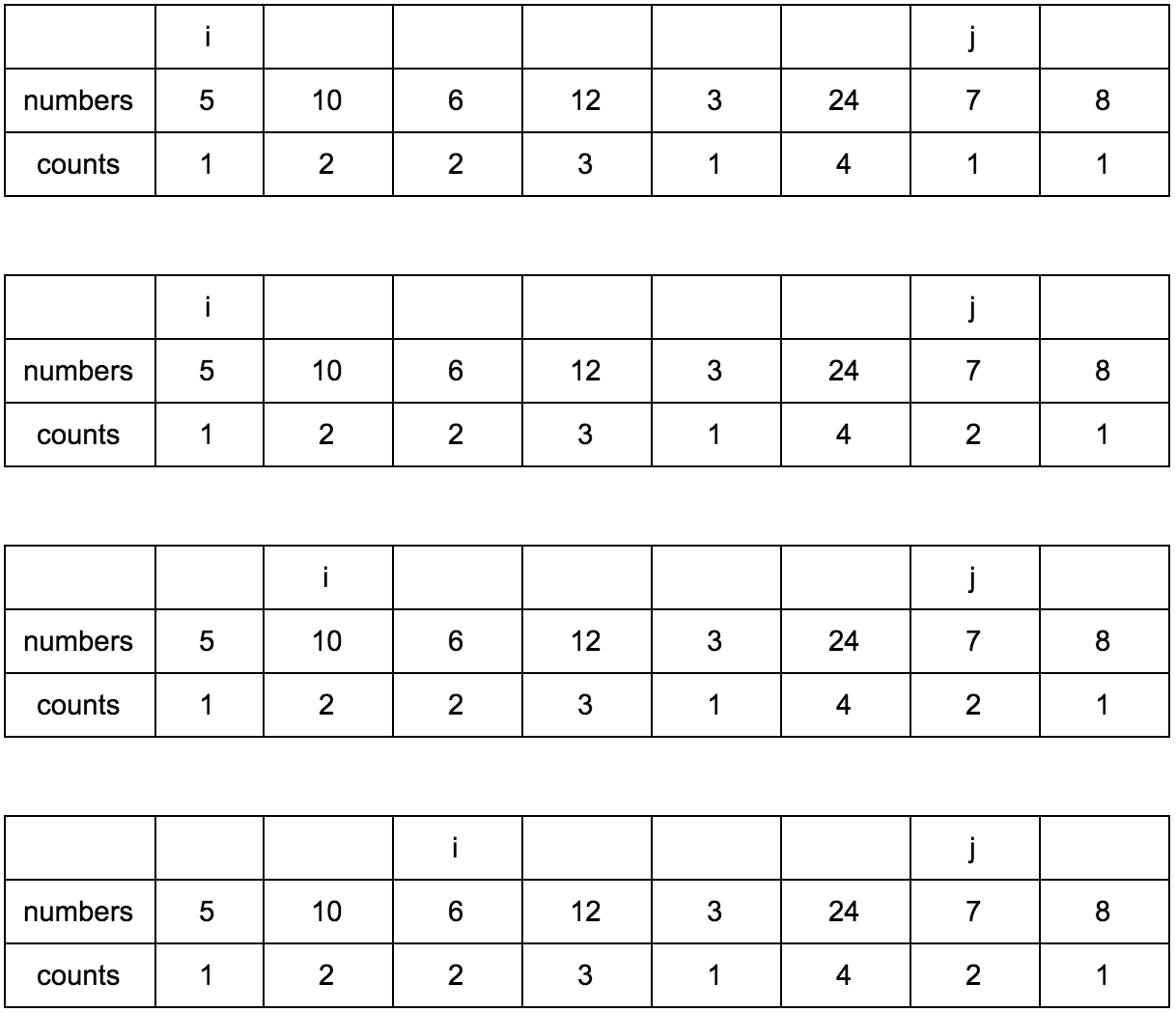
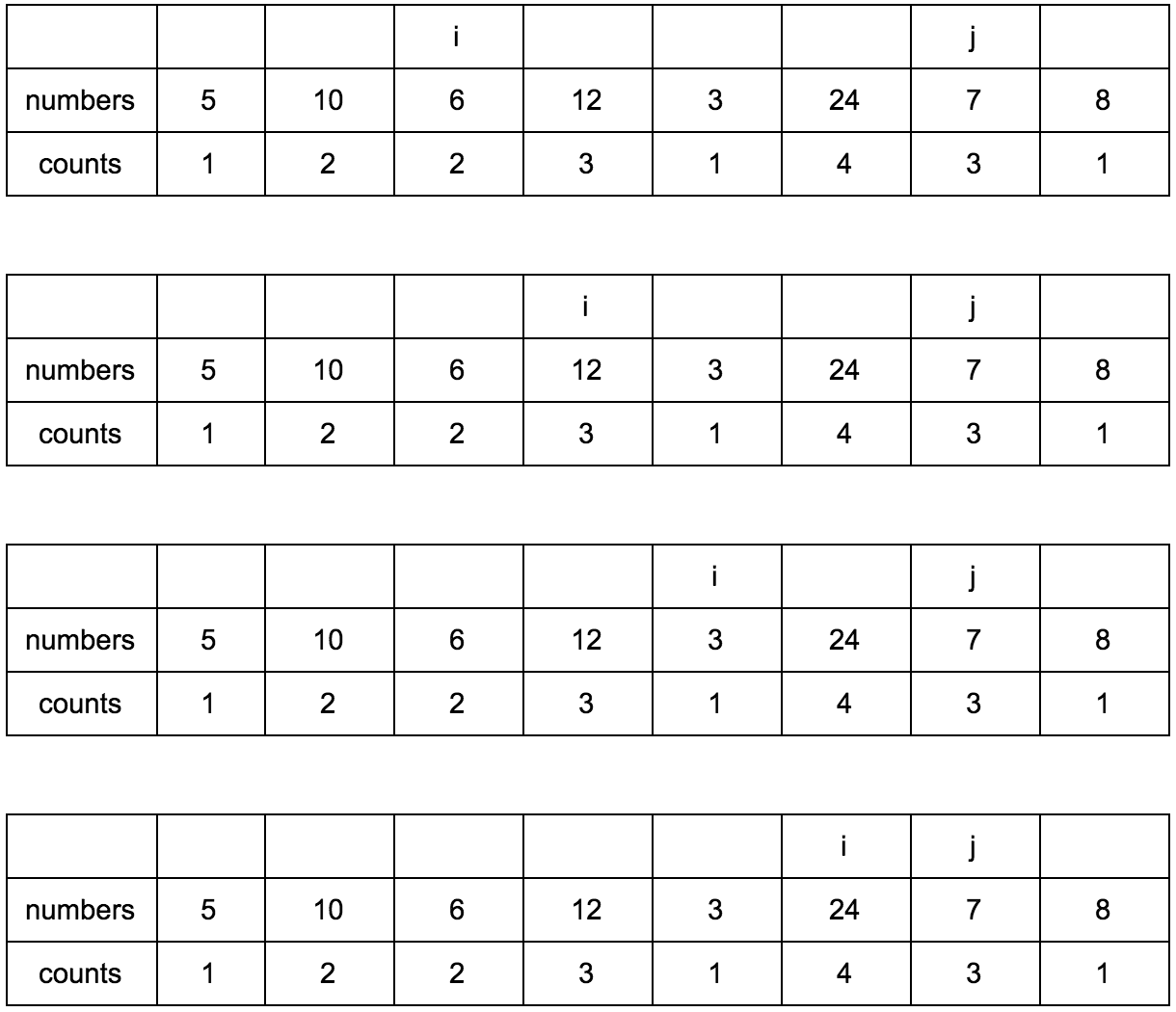
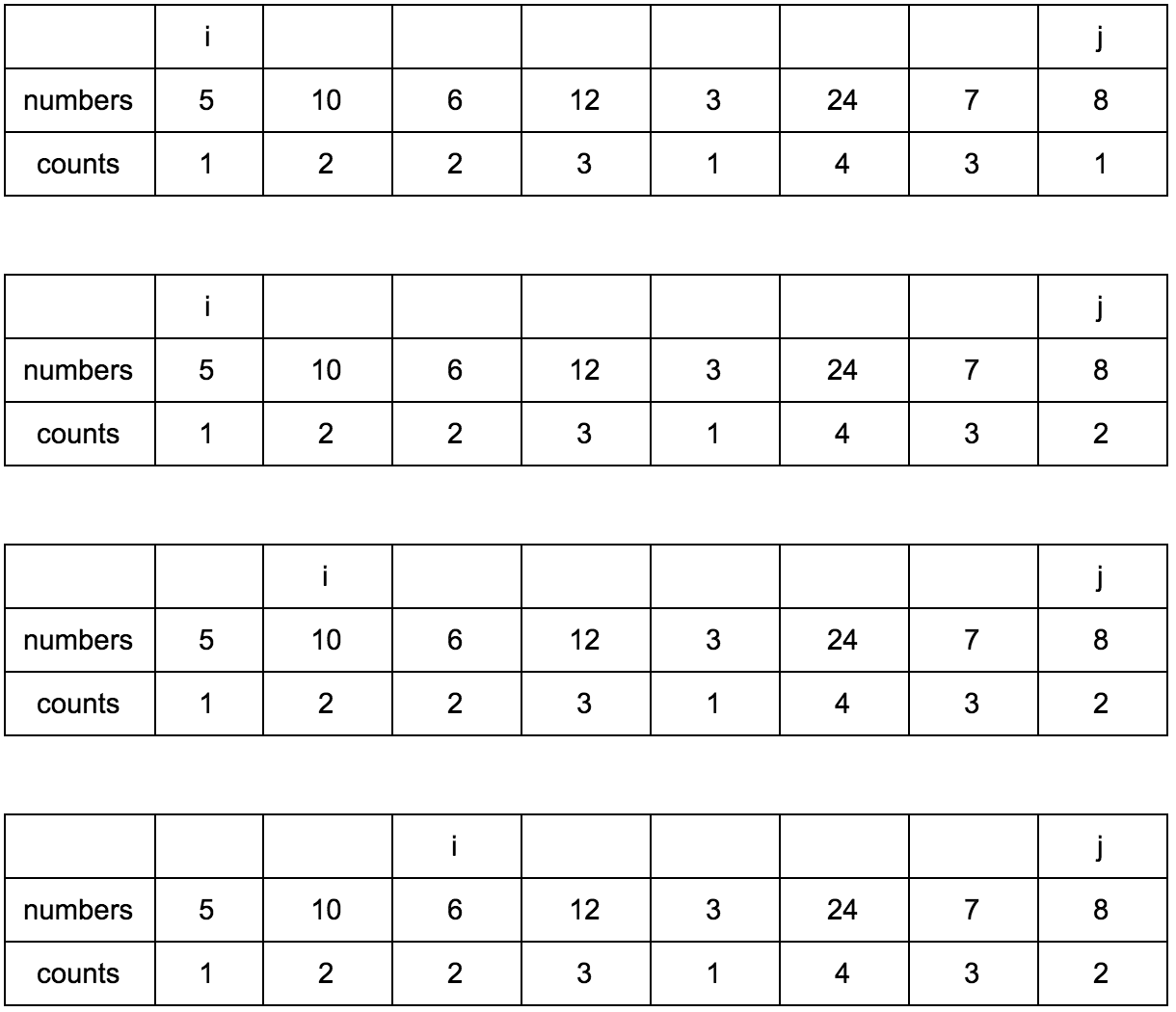
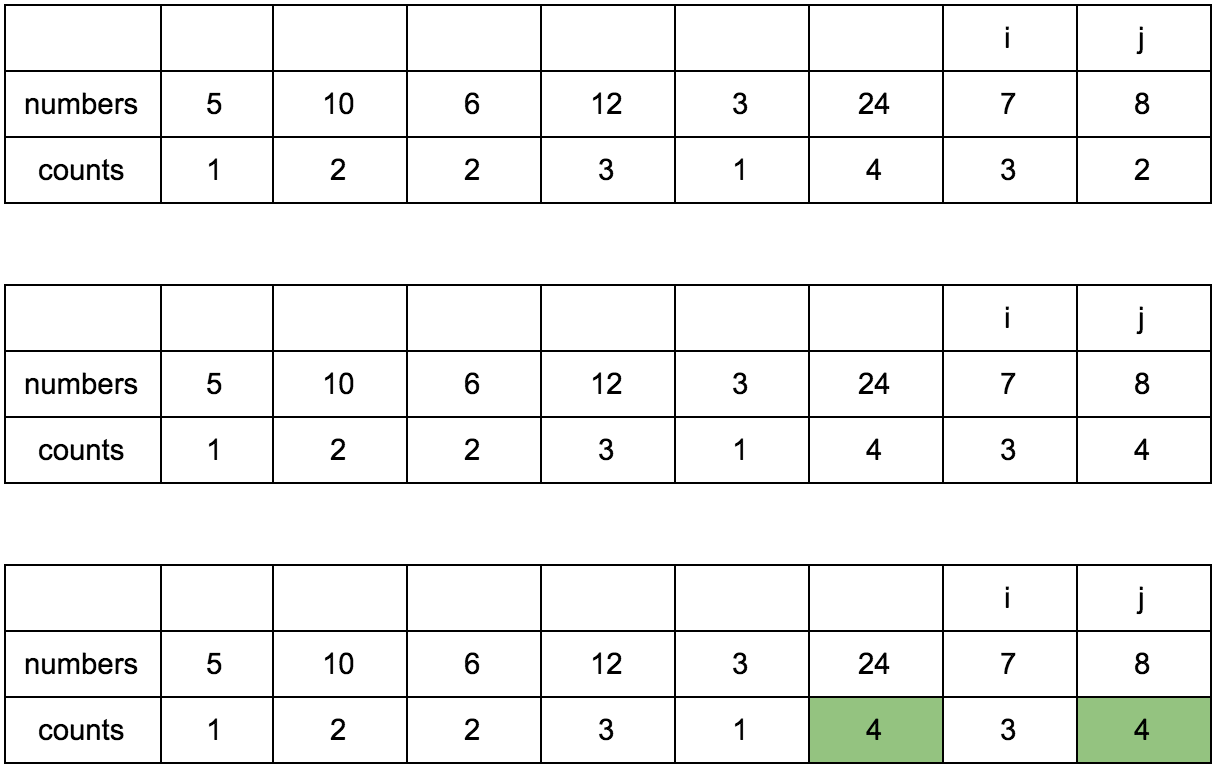
Результат:

Имея перед глазами эту таблицу и понимая какие шаги нужно делать, мы теперь легко можем реализовать это в коде.

int longestIncreasingSubsequenceLength( int numbers[]  ) {

    if (numbers.count == 1) {
        return 1;
    }

   int lengthOfSubsequence[] = Аrray.newArrayOfSize(numbers.count, 1);

    for (int j = 1; j < numbers.count; j++) {
        for (int k = 0; k < j; k++) {
            if (numbers[j] > numbers[k]) {
                if (lengthOfSubsequence[j] <= lengthOfSubsequence[k]) {
                 lengthOfSubsequence[j] = lengthOfSubsequence[k] + 1;
                }
            }
        }
    }

    int maximum = 0;

    for (int length in lengthOfSubsequence) {
        maximum = MAX(maximum, length);
    }

    return maximum;
}

> Реализация на Objective-C
> Тесты

Вы не могли не заметить два вложенных цикла в коде, а там где есть два вложенных цикла проходящих по одному массиву, есть и квадратичная сложность O(n^2), что обычно не есть хорошо.

Теперь, если вы билингвал, вы несомненно зададитесь вопросом “Can we do better?”, обычные же смертные спросят “Могу ли я придумать алгоритм, который сделает это за меньшее время?”

Ответ: “да, можете!”

Чтобы сделать это нам нужно вспомнить, что такое бинарный поиск.

Бинарный поиск O(log n)

Бинарный поиск работает только на отсортированных массивах. Например, нам нужно найти позицию числа n в отсортированном массиве:
1, 5, 6, 8, 14, 15, 17, 20, 22

Зная что массив отсортирован, мы всегда можем сказать правее или левее определенного числа в массиве искомое число должно находиться.

Мы ищем позицию числа 8 в этом массиве. С какой стороны от середины массива оно будет находиться? 14 — это число в середине массива. 8 < 14 — следовательно 8 левее 14. Теперь нас больше не интересует правая часть массива, и мы можем ее отбросить и повторять ту же самую операцию вновь и вновь пока не наткнемся на 8. Как видите, нам даже не нужно проходить по всем элементам массива, сложность этого алгоритма < O( n ) и равна O (log n).

Для реализации алгоритма нам понадобятся 3 переменные для индексов: left, middle, right.

Ищем позицию числа 8.

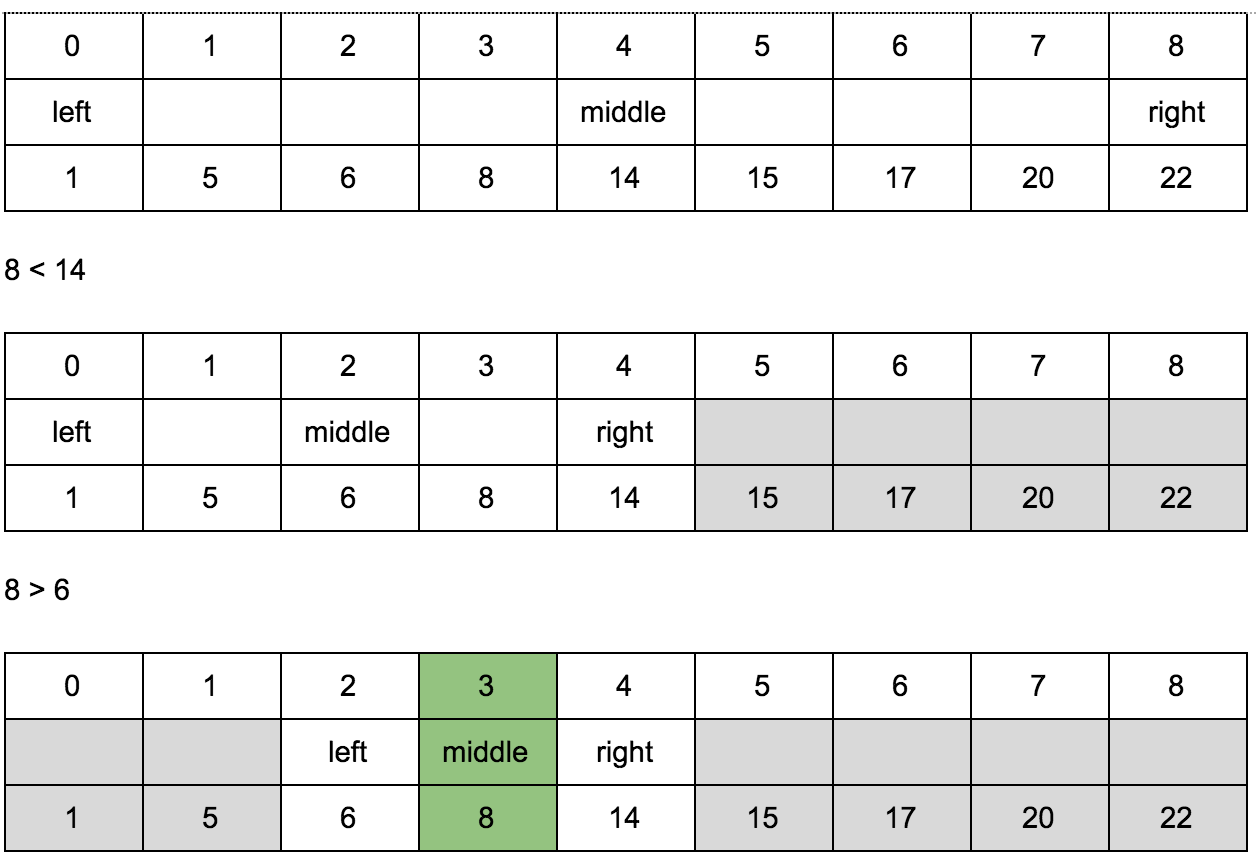
Мы отгадали где находится 8 с трёх нот.

int binarySearch(int list [], int value) {

    if !list.isEmpty {
        int left = list.startIndex
        int right = list.endIndex-1

        while left <= right {

            let middle = left + (right - left)/2

            if list[middle] == value{
                return middle
            }

            if value < list[middle]{
                right = middle - 1
            }
            else{
                left = middle + 1
            }
        }
    }
    return nil
}

Решение за O (n * log n)

Теперь мы будем проходить по нашему исходному массиву при этом заполняя новый массив, в котором будет храниться возрастающая подпоследовательность. Еще один плюс этого алгоритма: он находит не только длину максимальной возрастающей подпоследовательности, но и саму подпоследовательность.

Как же двоичный поиск поможет нам в заполнении массива подпоследовательности?

С помощью этого алгоритма мы будем искать место для нового элемента в вспомогательном массиве, в котором мы храним для каждой длины подпоследовательности минимальный элемент, на котором она может заканчиваться.

Если элемент больше максимального элемента в массиве, добавляем элемент в конец. Это просто.

Если такой элемент уже существует в массиве, ничего особо не меняется. Это тоже просто.

Что нам нужно рассмотреть, так это случай когда следующий элемент меньше максимального в этом массиве. Понятно, что мы не можем его поставить в конец, и он не обязательно вообще должен являться членом именно максимальной последовательности, или наоборот, та подпоследовательность, которую мы имеем сейчас и в которую не входит этот новый элемент, может быть не максимальной.

Все это запутанно, сейчас будет проще, сведем к рассмотрению 2-х оставшихся случаев.

1. Рассматриваемый элемент последовательности (x) меньше чем наибольший элемент в массиве (Nmax), но больше чем предпоследний.
2. Рассматриваемый элемент меньше какого-то элемента в середине массива.

В случае 1 мы просто можем откинуть Nmax в массиве и поставим на его место x. Так как понятно, что если бы последующие элементы были бы больше чем Nmax, то они будут и больше чем x — соответственно мы не потеряем ни одного элемента.

Случай 2: для того чтобы этот случай был нам полезен, мы заведем еще один массив, в котором будем хранить размер подпоследовательности, в которой этот элемент является максимальным. Собственно этим размером и будет являться та позиция в первом вспомогательном массиве для этого элемента, которую мы найдем с помощью двоичного поиска. Когда мы найдем нужную позицию, мы проверим элемент справа от него и заменим на текущий, если текущий меньше (тут действует та же логика как и в первом случае)

Не расстраивайтесь, если не все стало понятно из этого текстового объяснения, сейчас я покажу все наглядно.

Нам нужны:

1. Исходная последовательность
2. Создаем мутабельный массив, где будем хранить возрастающие элементы для подпоследовательности
3. Создаем мутабельный массив размеров подпоследовательности, в которой рассматриваемый элемент является максимальным.

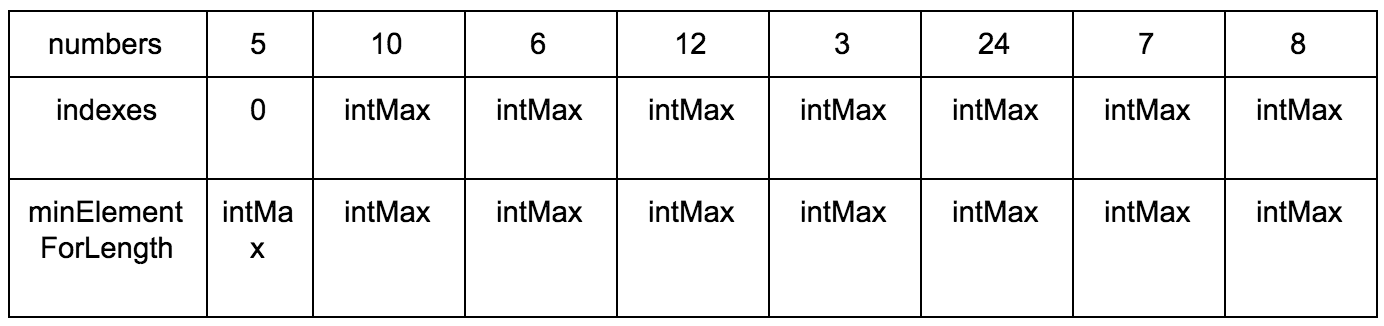
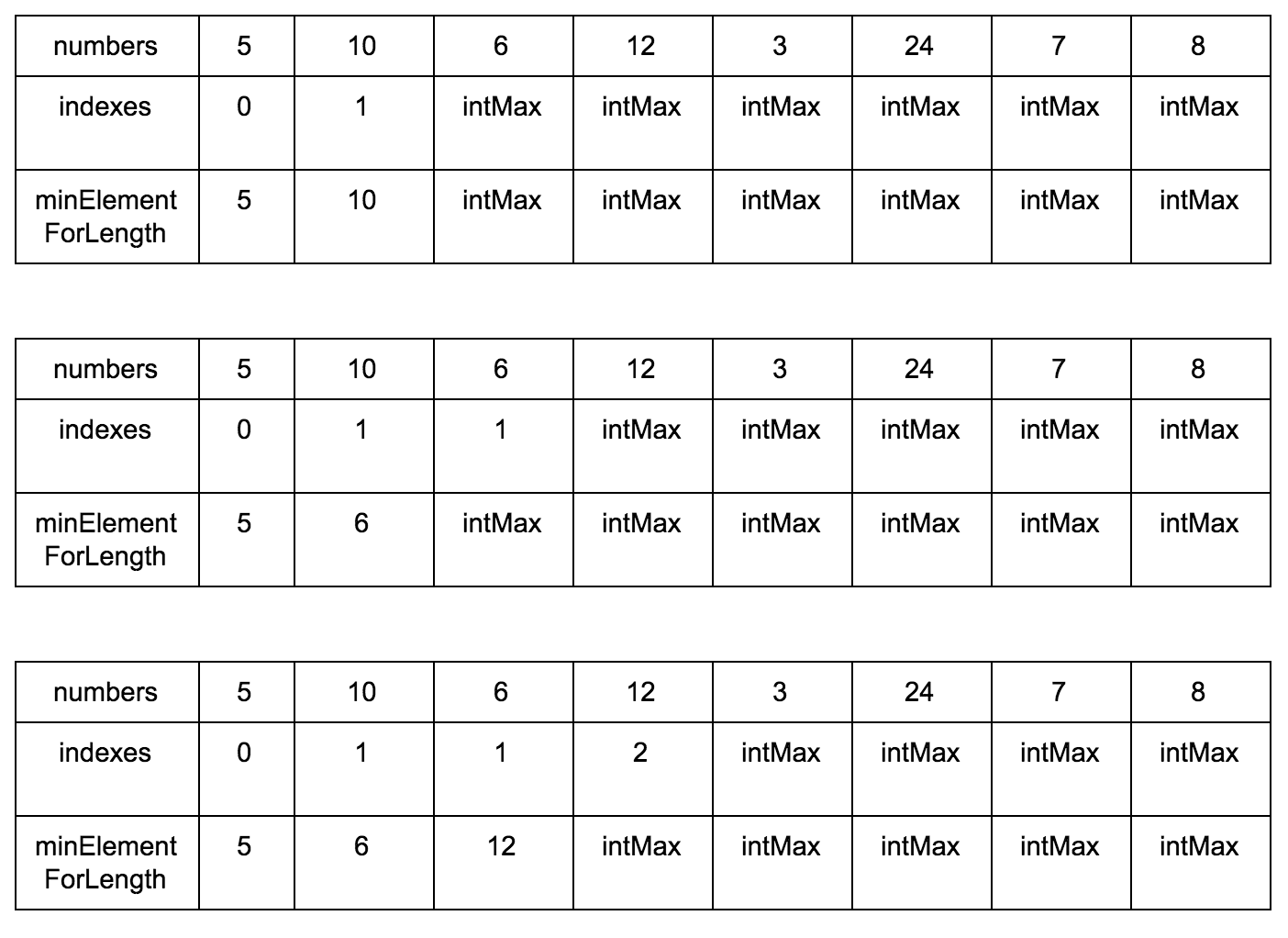
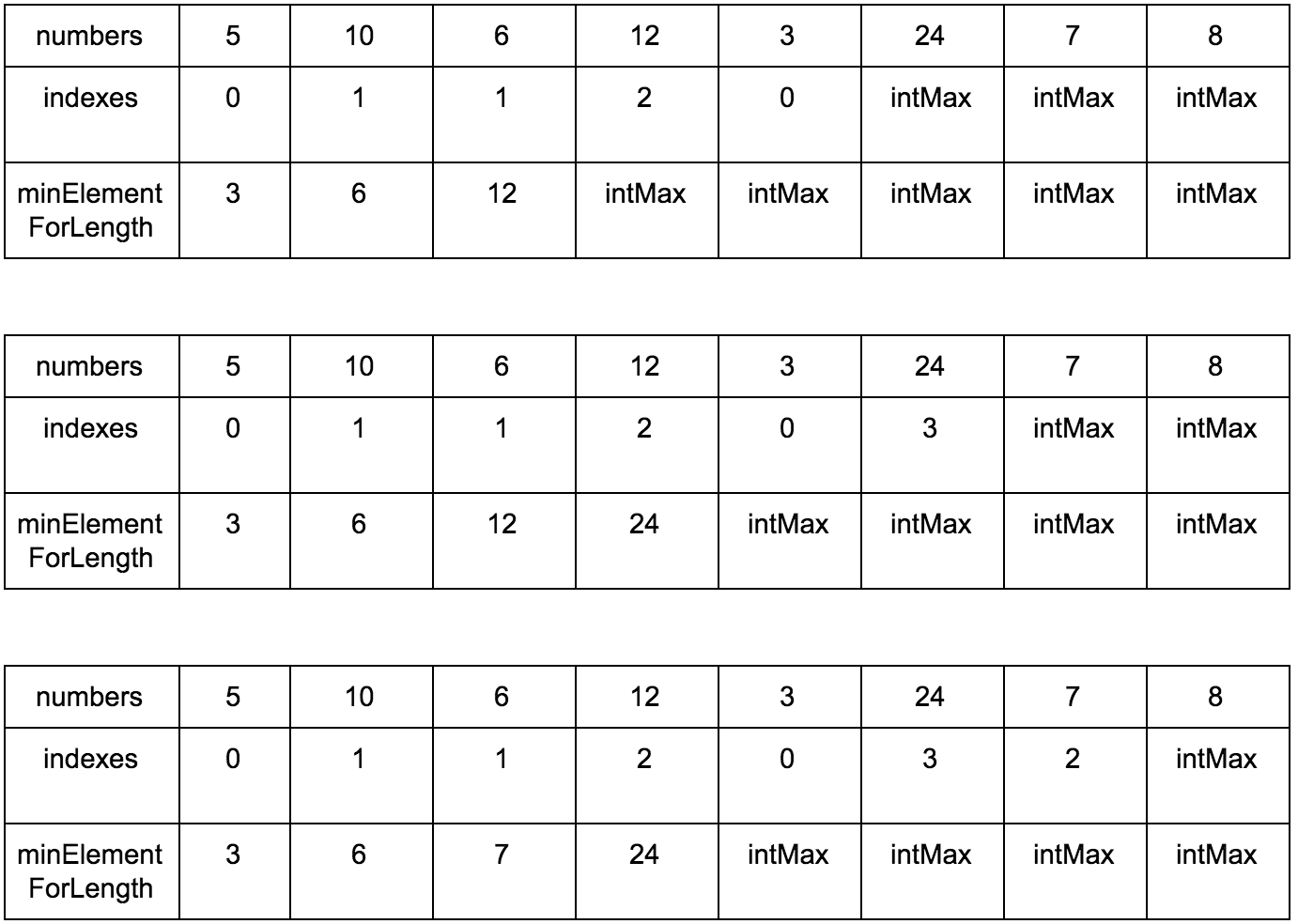
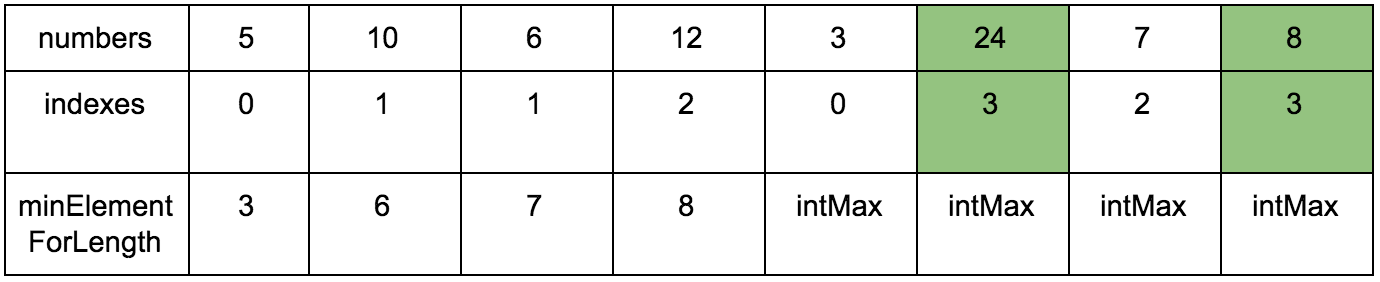
Результат:

int longestIncreasingSubsequenceLength(int numbers[]) {

    if (numbers.count <= 1) {
        return 1;
    }

    int lis_length = -1;

    int subsequence[];
    int indexes[];

    for (int i = 0; i < numbers.count; ++i) {
        subsequence[i] = INT_MAX;
        subsequence[i] = INT_MAX;
    }

    subsequence[0] = numbers[0];
    indexes[0] = 0;

    for (int i = 1; i < numbers.count; ++i) {
        indexes[i] = ceilIndex(subsequence, 0, i, numbers[i]);

        if (lis_length < indexes[i]) {
            lis_length = indexes[i];
        }
    }

    return lis_length + 1;
}

int ceilIndex(int subsequence[], 
              int startLeft, 
              int startRight,
              int key){

    int mid = 0;
    int left = startLeft;
    int right = startRight;
    int ceilIndex = 0;
    bool ceilIndexFound = false;

    for (mid = (left + right) / 2; left <= right && !ceilIndexFound; mid = (left + right) / 2) {
        if (subsequence[mid] > key) {
            right = mid - 1;
        }
        else if (subsequence[mid] == key) {
            ceilIndex = mid;
            ceilIndexFound = true;
        }
        else if (mid + 1 <= right && subsequence[mid + 1] >= key) {
            subsequence[mid + 1] = key;
            ceilIndex = mid + 1;
            ceilIndexFound = true;
        } else {
            left = mid + 1;
        }
    }

    if (!ceilIndexFound) {
        if (mid == left) {
            subsequence[mid] = key;
            ceilIndex = mid;
        }
        else {
            subsequence[mid + 1] = key;
            ceilIndex = mid + 1;
        }
    }

    return ceilIndex;
}

> Реализация на Objective-C
> Тесты

Итоги

Мы с вами сейчас рассмотрели 4 алгоритма разной сложности. Это сложности, с которыми вам приходится встречаться постоянно при анализе алгоритмов:

О( log n ), О( n ), О( n * log n ), О( n ^ 2 )

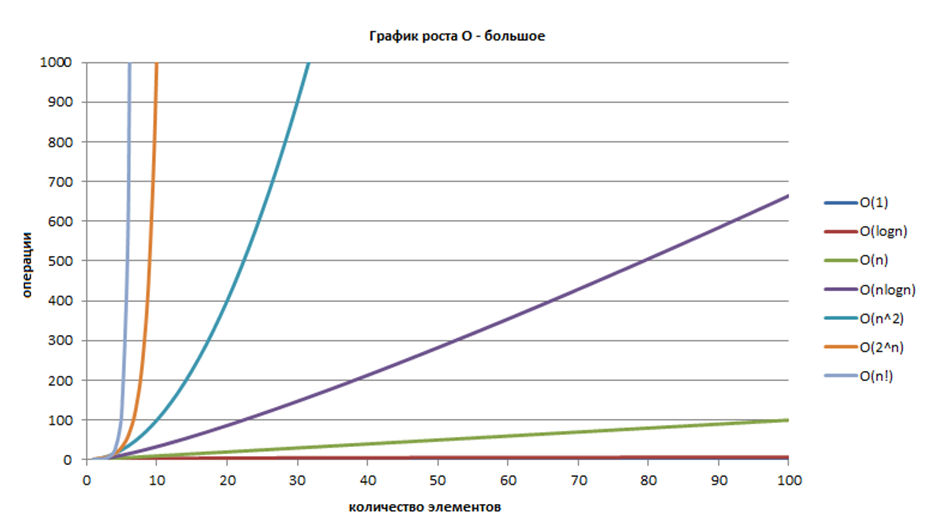
Эта картинка из вот этой статьи

Еще мы рассмотрели примеры использования Динамического Программирования, тем самым расширив наш инструмент разработки и понимания алгоритмов. Эти принципы пригодятся вам при изучении других проблем.

Для лучшего понимания я рекомендую вам закодировать эти проблемы самим на привычном вам языке. А еще было бы здорово, если бы вы запостили ссылку на ваше решение в комментах.

Еще предлагаю подумать над тем как доработать последний алгоритм за O (n * log n ) так чтобы вывести еще и саму наибольшую подпоследовательность. Ответ напишите в комментах.

Всем спасибо за внимание, до новых встреч!

Ссылки:
Вопрос на Stackoverflow.com
Примеры реализации на C++ и Java
Видео с объяснением