Начну с двух простых вопросов с достаточно интуитивными ответами. Возьмём чашу и шарик (рис. 1). Если мне нужно, чтобы:

• шарик оставался неподвижным после того, как я помещу его в чашу, и
• он оставался примерно в том же положении при перемещении чаши,

то куда мне его положить?


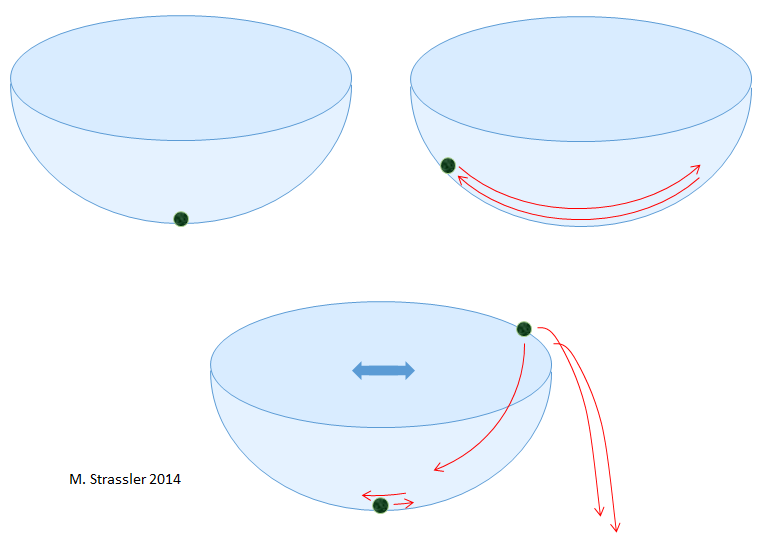
Рис. 1

Конечно, мне нужно положить его в центр, на самое дно. Почему? Интуитивно ясно, что если я положу его куда-то ещё, он скатится до дна, и будет болтаться туда и сюда. В итоге трение уменьшит высоту болтаний и затормозит его внизу.

В принципе можно попробовать уравновесить шарик на краю чаши. Но если я немного потрясу её, шарик потеряет равновесие у падёт. Так что это место не удовлетворяет второму критерию в моём вопросе.

Назовём положение, в котором шарик остаётся неподвижным, и от которого он не сильно отклоняется при небольших движениях чаши или шарика, «стабильным положением шарика». Дно чаши — такое стабильное положение.

Другой вопрос. Если у меня есть две чаши, как на рис. 2, где будут стабильные положения для шарика? Это тоже просто: таких мест два, а именно, на дне каждой из чаш.


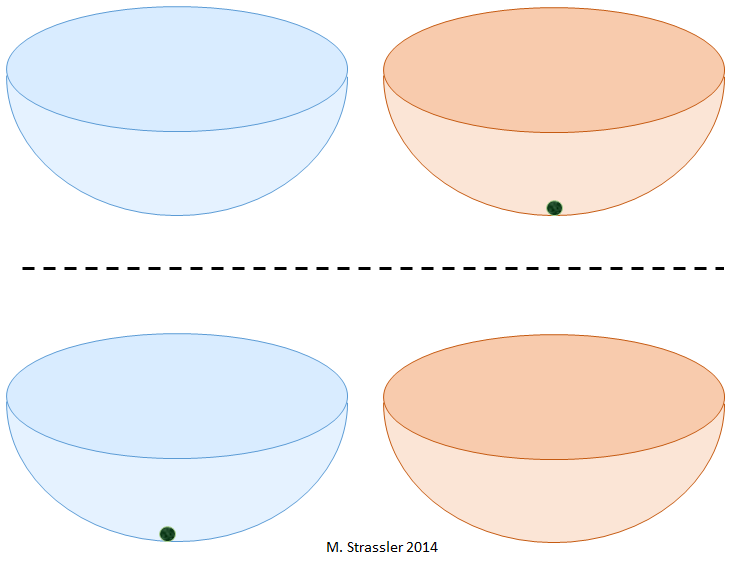
Рис. 2

Наконец, ещё один вопрос с интуитивно понятным ответом. Если я размещу шарик на дне чаши 1, а потом выйду из комнаты, закрою её, гарантирую, что никто туда не зайдёт, проверю, что в этом месте не было землетрясений и других потрясений, то каковы шансы, что через десять лет, когда я вновь открою комнату, я обнаружу шарик на дне чаши 2? Конечно, нулевые. Чтобы шарик переместился со дна чаши 1 на дно чаши 2, кто-то или что-то должны взять шарик и переместить его с места на место, над краем чаши 1, в сторону чаши 2 и затем над краем чаши 2. Очевидно, что шарик останется на дне чаши 1.

Очевидно и по сути верно. И всё же, в квантовом мире, в котором мы живём, ни один объект не остаётся по-настоящему неподвижным, и его положение точно неизвестно. Так что ни один из этих ответов не верен на 100%.

Туннелирование

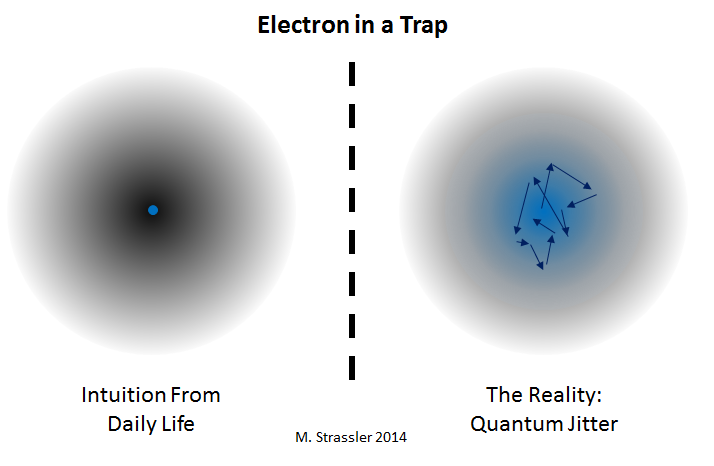
Рис. 3

Если я размещу элементарную частицу вроде электрона в магнитной ловушке (рис. 3) работающей, как чаша, стремящейся подтолкнуть электрон к центру точно так же, как гравитация и стены чаши толкают шарик к центру чаши на рис. 1, тогда каково будет стабильное положение электрона? Как и следовало интуитивно ожидать, среднее положение электрона будет стационарным, только если разместить его в центре ловушки.

Но квантовая механика добавляет один нюанс. Электрон не может оставаться неподвижным; его положение подвержено «квантовому дрожанию». Из-за этого его положение и движение постоянно меняется, или даже обладает некоей долей неопределённости (это работает знаменитый «принцип неопределённости»). Только среднее положение электрона находится в центре ловушки; если посмотреть на электрон, то он окажется где-нибудь в другом месте ловушки, рядом с центром, но не совсем там. Электрон неподвижен только в таком смысле: он обычно двигается, но его движение случайное, и поскольку он находится в ловушке, в среднем он никуда не сдвигается.

Это немного странно, но всего лишь отражает тот факт, что электрон представляет собой не то, что вы думаете, и не ведёт себя так, как любой из виденных вами объектов.

Это, кстати, также гарантирует, что электрон нельзя уравновесить на краю ловушки, в отличие от шарика на краю чаши (как внизу на рис. 1). Положение электрона не определено точно, поэтому его нельзя точно уравновесить; поэтому, даже без встряхиваний ловушки, электрон потеряет равновесие и почти сразу сорвётся.

Но что более странно, так это тот случай, когда у меня будет две ловушки, отделённые друг от друга, и я размещу электрон в одной из них. Да, центр одной из ловушек — хорошее, стабильное положение для электрона. Это так — в том смысле, что электрон может оставаться там и не убежит, если потрясти ловушку.

Однако, если разместить электрон в ловушке №1, и уйти, закрыть комнату и т.п., существует определённая вероятность того (рис. 4), что, когда я вернусь электрон будет находиться в ловушке №2.


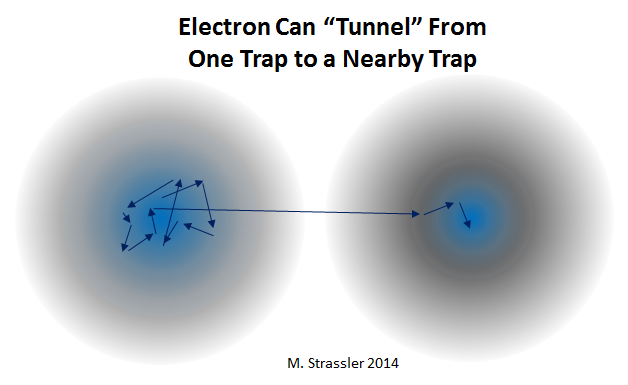
Рис. 4

Как он это сделал? Если представлять себе электроны в виде шариков, вы этого не поймёте. Но электроны не похожи на шарики (или, по крайней мере, на ваше интуитивное представление о шариках), и их квантовое дрожание даёт им крайне небольшой, но ненулевой шанс «прохода сквозь стены» — кажущаяся невероятной возможность переместиться на другую сторону. Это называется туннелированием — но не надо думать, что электрон прокапывает дырку в стене. И вы никогда не сможете поймать его в стене — так сказать, с поличным. Просто стена не полностью непроницаема для таких вещей, как электрон; электроны нельзя так легко поймать в ловушку.

На самом деле, всё ещё безумнее: поскольку это правда для электрона, это правда и для шарика в вазе. Шарик может оказаться в вазе 2, если подождать достаточно долго. Но вероятность этого чрезвычайно мала. Так мала, что даже если подождать миллиард лет, или даже миллиарды миллиардов миллиардов лет, этого будет недостаточно. С практической точки зрения этого «никогда» не произойдёт.

Наш мир — квантовый, и все объекты состоят из элементарных частиц и подчиняются правилам квантовой физики. Квантовое дрожание присутствует постоянно. Но большая часть объектов, масса которых велика по сравнению с массой элементарных частиц — шарик, к примеру, или даже пылинка — это квантовое дрожание слишком мелкое, чтобы его обнаружить, за исключением особо разработанных экспериментов. И следующая из этого возможность туннелировать сквозь стены тоже не наблюдается в обычной жизни.

Иначе говоря: любой объект может туннелировать сквозь стену, но вероятность этого обычно резко уменьшается, если:

• у объекта большая масса,
• стена толстая (большое расстояние между двумя сторонами),
• стену трудно преодолеть (чтобы пробить стену, нужно много энергии).

В принципе шарик может преодолеть край чаши, но на практике это может оказаться невозможным. Электрону может быть легко сбежать из ловушки, если ловушки расположены близко и не очень глубокие, но может быть и очень сложно, если они расположены далеко и очень глубокие.

А точно туннелирование происходит?

Рис. 5

А может, это туннелирование — просто теория? Точно нет. Оно фундаментально для химии, происходит во многих материалах, играет роль в биологии, и это принцип, используемый в наших самых хитрых и мощных микроскопах.

Для краткости давайте я остановлюсь на микроскопе. На рис. 5 представлено изображение атомов, сделанное при помощи сканирующего туннельного микроскопа. У такого микроскопа есть узкая игла, чей кончик двигается в непосредственной близости к изучаемому материалу (см. рис. 6). Материал и иголка, разумеется, состоят из атомов; а на задворках атомов находятся электроны. Грубо говоря, электроны находятся в ловушке внутри изучаемого материала или на кончике микроскопа. Но чем ближе кончик к поверхности, тем более вероятен туннельный переход электронов между ними. Простое устройство (между материалом и иглой поддерживается разница потенциалов) гарантирует, что электроны предпочтут перескакивать с поверхности на иглу, и этот поток — электрический ток, поддающийся измерению. Игла двигается над поверхностью, и поверхность оказывается то ближе, то дальше от кончика, и ток меняется — становится сильнее с уменьшением расстояния и слабее с увеличением. Отслеживая ток (или, наоборот, двигая иглу вверх и вниз для поддержания постоянного тока) при сканировании поверхности, микроскоп делает вывод о форме этой поверхности, и часто детализации хватает для того, чтобы разглядеть отдельные атомы.


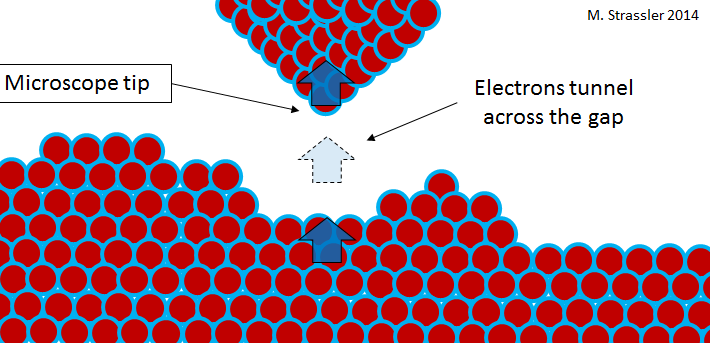
Рис. 6

Туннелирование играет и множество других ролей в природе и современных технологиях.

Туннелирование между ловушками разной глубины

На рис. 4 я подразумевал, что у обеих ловушек одинаковая глубина — точно так же, как у обеих чаш на рис. 2 одинаковая форма. Это означает, что электрон, находясь в любой из ловушек, с одинаковой вероятностью перескочит в другую.

Теперь допустим, что одна ловушка для электрона на рис. 4 глубже другой — точно так же, как если бы одна чаша на рис. 2 была глубже другой (см. рис. 7). Хотя электрон может туннелировать в любом направлении, ему будет гораздо проще туннелировать из более мелкой в более глубокую ловушку, чем наоборот. Соответственно, если мы подождём достаточно долго, чтобы у электрона было достаточно времени туннелировать в любом направлении и вернуться, а затем начнём проводить измерения с целью определить его местонахождение, мы чаще всего будем находить его в глубокой ловушке. (На самом деле и тут есть свои нюансы, всё зависит ещё и от формы ловушки). При этом разница глубин не обязательно должна быть крупной для того, чтобы туннелирование из более глубокой в более мелкую ловушку стало чрезвычайно редким.

Короче, туннелирование в целом будет происходить в обоих направлениях, но вероятность перехода из мелкой ловушки в глубокую гораздо больше.


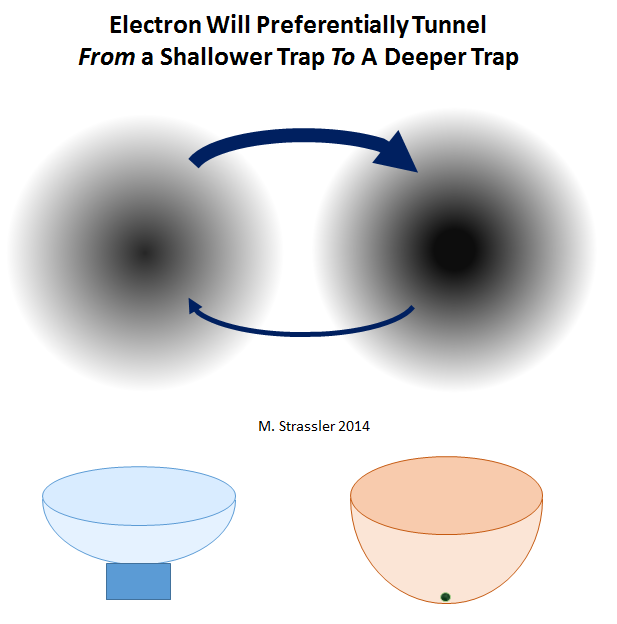
Рис. 7

Именно эта особенность используется в сканирующем туннельном микроскопе, чтобы гарантировать, что электроны будут переходить только в одном направлении. По сути кончик иглы микроскопа оказывается более глубокой ловушкой, чем изучаемая поверхность, поэтому электроны предпочитают туннелировать из поверхности на иглу, а не наоборот. Но микроскоп будет работать и в противоположном случае. Ловушки делаются глубже или мельче при помощи источника питания, создающего разность потенциалов между иглой и поверхностью, что создаёт разницу в энергиях у электронов на игле и электронов на поверхности. Поскольку заставить электроны чаще туннелировать в одном направлении, чем в другом, оказывается довольно просто, это туннелирование становится практически полезным для использования в электронике.