
Введение
В 1934 году швейцарская фирма «БроунБовери» (Brown-Boveri) на основе теоретических работ Стодолы впервые создала многоступенчатый осевой компрессор с КПД 84 %. Вскоре, осевые компрессоры стали успешно использоваться этой фирмой для газотурбинных установок.
Многоступенчатые осевые компрессоры [1]
Принципиальная схема осевого многоступенчатого компрессора приведена на рисунке:

Осевой многоступенчатый компрессор состоит из ряда последовательно расположенных направляющих лопаток 6, закрепленных в корпусе 7, и рабочих лопаток 5, расположенных на барабанном роторе 11. По мере сжатия, объем воздуха уменьшается и, следовательно, уменьшаются высоты лопаток.
Вращаясь, рабочие лопатки ротора сообщают газу кинетическую энергию. При движении по расширяющимся каналам рабочих лопаток относительная скорость воздуха падает, происходит уменьшение кинетической энергии потока с соответствующим повышением давления в нем.
Изменение относительной скорости потока в канале рабочих лопаток связано с расходом энергии, подводимой к компрессору.
В расширяющихся каналах направляющих лопаток наблюдается дальнейшее повышение давления воздуха и уменьшение скорости его движения. В проточную часть компрессора воздух поступает через входной патрубок 1 и направляющий аппарат 4, откуда, пройдя каналы рабочих лопаток 5 и направляющих лопаток 6, попадает в спрямляющий аппарат 8.
Направляющий аппарат обеспечивает необходимое направление воздушному потоку перед входом в первую ступень, а спрямляющий аппарат обеспечивает осевой выход в диффузор 9 и далее в выходной патрубок 10.
Число ступеней сжатия в такой конструкции определяется количеством рабочих лопаток 5, расположенных на барабанном роторе 11.
Многоступенчатые поршневые компрессоры [2]
Для получения сжатого газа более высокого давления (0,1-2 МПа и выше) применяются многоступенчатые компрессоры с промежуточным охлаждением газа после каждой ступени.
Сущность многоступенчатого сжатия может быть пояснена на примере двухступенчатого компрессора, схема которого и идеальная (при Vo = 0) индикаторная диаграмма представлена на рисунке:

В первой ступени 1 газ сжимается по политропе 1–2 до давления Р2, а затем он поступает в промежуточный холодильник 3, где охлаждается до начальной температуры T1. Гидравлическое сопротивление холодильника по воздушному тракту делают небольшим. Это позволяет считать процесс охлаждения 2–3 изобарным.
После холодильника газ поступает во вторую ступень 2, где сжимается по политропе 3–4 до давления Р3. Если бы сжатие до давления Р3 осуществлялось в идеальном одноступенчатом компрессоре (линия 1–2'), то величина затраченной за цикл работы определялась бы площадью 012'b0.
При двухступенчатом сжатии с промежуточным охлаждением, эта работа численно равна площади 01234b0. Заштрихованная площадь соответствует экономии работы за цикл при двухступенчатом сжатии.
Многоступенчатое сжатие газа [3]
При многоступенчатом изоэнтропическом сжатии газа от начального давления Po до конечного давления Pn, желательно, установить такие промежуточные давления, при которых суммарная энергия, израсходованная на сжатие, была бы минимальной.
Газ охлаждается изобарический до своей начальной температуры T, после каждого адиабатического сжатия. Затраты энергии на n- ступени определяются из уравнения:

где: m- число кмолей сжимаемого газа;R-универсальная газовая постоянная,
 ;
; T — начальная температура газа, K; ? — отношение удельных теплоемкостей газа при постоянном давлении и постоянном объеме, в работе принято ?=1,4; xn- давление газа после сжатия на n ступени.
Постановка задачи
1. Найти такое распределение давлений на выходе ступеней адиабатического сжатия
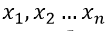 при котором затраченная на сжатие энергия
при котором затраченная на сжатие энергия 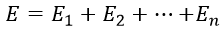 , будет минимальна;
, будет минимальна;2. Определить влияние числа степеней сжатия на минимальную энергию сжатия при одинаковых значениях начального и конечного давлений.
Решение задачи средствами библиотеки scipy. optimize
Сначала рассмотрим пять степеней сжатия в соответствии с расчётной схемой, приведенной на рисунке:

#!/usr/bin/env python
#coding=utf8
import numpy as np# модуль для создания списков
from scipy.optimize import minimize# модуль оптимизации
import matplotlib.pyplot as plt# модуль для графиков
import time# модуль для контроля времени
Po=1#начальное давление газа
Pzad=64#конечное давление газа
g=1.4#отношение удельных теплоемкостей газа
m=10# число кило моль газа
R=8.314# универсальная газовая постоянная
a=(g-1)/g
T=293# температура газа
a=0.286
"Распределение энергии по ступеням сжатия:"
def E1(x1):
return m*R*T*a*((x1/Po)**2-1)
def E2(x1,x2):
return m*R*T*a*((x2/x1)**2-1)
def E3(x2,x3):
return m*R*T*a*((x3/x2)**2-1)
def E4(x3,x4):
return m*R*T*a*((x4/x3)**2-1)
def E5(x4):
return m*R*T*a*((Pzad/x4)**2-1)
start = time.time()
def E(x1,x2,x3,x4):#
return E1(x1)+E2(x1,x2)+E3(x2,x3)+E4(x3,x4)+E5(x4)
def fun2(x):
return E(*x)
x0 =[4,15,24,40] #точка начала поиска экстремума
res = minimize(fun2, x0)# распределение давления при минимуме энергии
stop = time.time()
print ("Время работы оптимизатора:",round(stop-start,3))
x1=round(res['x'][0],3)#давление на выходе I ступени
x2=round(res['x'][1],3)#давление на выходе II ступени
x3=round(res['x'][2],3)#давление на выходе III ступени
x4=round(res['x'][3],3)#давление на выходе IV ступени
x5=Pzad
"Формирование списка давлений:"
x=[]
x.append(x1)
x.append(x2)
x.append(x3)
x.append(x4)
x.append(x5)
z1=E1(x1)# затраты энергии I ступени
z2=E2(x1,x2)+z1# общие затраты энергии I+II ступени
z3=E3(x2,x3)+z2#общие затраты энергии I+II +III ступени
z4=E4(x3,x4)+z3#общие затраты энергии I+II +III +IV ступени
z5=E5(x4)+z4#общие затраты энергии I+II +III +IV+V ступени
"Формирование списка затрат энергии:"
y=[]
y.append(z1)
y.append(z2)
y.append(z3)
y.append(z4)
y.append(z5)
plt.title('Затраты энергии - %s кДж на %s ступенчатое \nадиабатическое сжатие газа с %s до %s ати '%(int(z5),len(y),Po,Pzad))
plt.ylabel('Затраты энергии')
plt.xlabel('Давление газа')
plt.plot(x[0],y[0],'o', label='I ступень, давление - %s'%x1)
plt.plot(x[1],y[1],'o', label='II ступень, давление - %s'%x2)
plt.plot(x[2],y[2],'o', label='III ступень, давление - %s'%x3)
plt.plot(x[3],y[3],'o', label='IV ступень, давление - %s'%x4)
plt.plot(x[4],y[4],'o', label='V ступень, давление - %s'%x5)
plt.plot(x,y,'r')
plt.legend(loc='best')
plt.grid(True)
plt.show()Получим:
Время работы оптимизатора: 0.0

Увеличим количество ступеней сжатия на одну согласно следующего листинга:
#!/usr/bin/env python
#coding=utf8
import numpy as np# модуль для создания списков
from scipy.optimize import minimize#модуль оптимизации
import matplotlib.pyplot as plt#модуль для графиков
import time# модуль для контроля времени
Po=1#начальное давление газа
Pzad=64#конечное давление газа
g=1.4#отношение удельных теплоемкостей газа
m=10# число кило моль газа
R=8.314# универсальная газовая постоянная
a=(g-1)/g
T=293# температура газа
a=0.286
"Распределение энергии по ступеням сжатия:"
def E1(x1):
return m*R*T*a*((x1/Po)**2-1)
def E2(x1,x2):
return m*R*T*a*((x2/x1)**2-1)
def E3(x2,x3):
return m*R*T*a*((x3/x2)**2-1)
def E4(x3,x4):
return m*R*T*a*((x4/x3)**2-1)
def E5(x4,x5):
return m*R*T*a*((x5/x4)**2-1)
def E6(x5):
return m*R*T*a*((Pzad/x5)**2-1)
start = time.time()
def E(x1,x2,x3,x4,x5):
return E1(x1)+E2(x1,x2)+E3(x2,x3)+E4(x3,x4)+E5(x4,x5)+E6(x5)
def fun2(x):
return E(*x)
x0 =[4,15,20,30,40]#точка начала поиска экстремума
res = minimize(fun2, x0)# распределение давления при минимуме энергии
stop = time.time()
print ("Время работы оптимизатора :",round(stop-start,3))
x1=round(res['x'][0],3)#давление на выходе I ступени
x2=round(res['x'][1],3)#давление на выходе II ступени
x3=round(res['x'][2],3)#давление на выходе III ступени
x4=round(res['x'][3],3)#давление на выходе IV ступени
x5=round(res['x'][4],3)#давление на выходе V ступени
x6=Pzad# давление на выходе VI ступени
"Формирование списка давлений:"
x=[]
x.append(x1)
x.append(x2)
x.append(x3)
x.append(x4)
x.append(x5)
x.append(x6)
z1=E1(x1)# затраты энергии I ступени
z2=E2(x1,x2)+z1# общие затраты энергии I+II ступени
z3=E3(x2,x3)+z2# общие затраты энергии I+II+III ступени
z4=E4(x3,x4)+z3# общие затраты энергии I+II+III+IV ступени
z5=E5(x4,x5)+z4# общие затраты энергии I+II+III+IV+V ступени
z6=E6(x5)+z5# общие затраты энергии I+II+III+IV+V +VI ступени
"Формирование списка затрат энергии:"
y=[]
y.append(z1)
y.append(z2)
y.append(z3)
y.append(z4)
y.append(z5)
y.append(z6)
plt.title('Затраты энергии - %s кДж на %s ступенчатое \nадиабатическое сжатие газа с %s до %s ати '%(int(z6),len(y),Po,Pzad))
plt.ylabel('Затраты энергии')
plt.xlabel('Давление газа')
plt.plot(x[0],y[0],'o', label='I ступень, давление - %s'%x1)
plt.plot(x[1],y[1],'o', label='II ступень, давление - %s'%x2)
plt.plot(x[2],y[2],'o', label='III ступень, давление - %s'%x3)
plt.plot(x[3],y[3],'o', label='IV ступень, давление - %s'%x4)
plt.plot(x[4],y[4],'o', label='V ступень, давление - %s'%x5)
plt.plot(x[5],y[5],'o', label='VI ступень, давление - %s'%x6)
plt.plot(x,y,'r')
plt.legend(loc='best')
plt.grid(True)
plt.show()Получим:
Время работы оптимизатора: 0.005
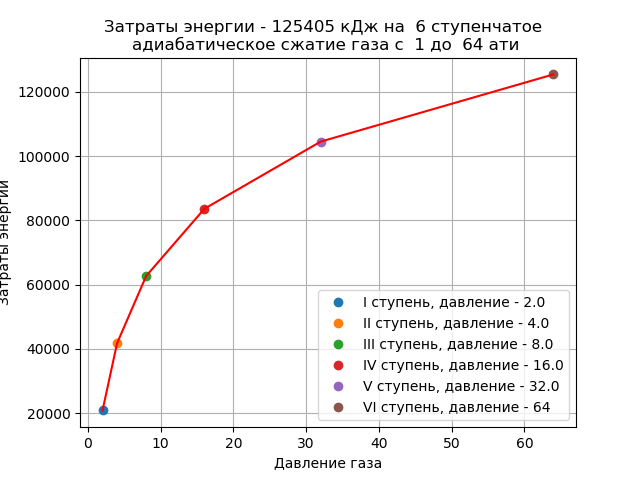
Сравнивая приведенные графики, можно определить снижение энергозатрат на адиабатическое сжатие газа:
(149024 -125405)*100/149024=15, 85%
Вывод: увеличение числа ступеней сжатия только на единицу позволяет сэкономить почти 16 % энергии, затраченной на адиабатическое сжатие газа в многоступенчатом компрессоре.
Однако, это только один вид затрачиваемой энергии. Понятно, что введение дополнительной ступени приведёт не только к дополнительным затратам при изготовлении, но и к дополнительным эксплуатационным затратам, за счёт увеличения мощности двигателя и секции системы охлаждения.
Оптимальный вариант нужно выбирать с учётом всех видов затрат, но это уже совсем другая задача.
Выводы:
1. Найдено распределение давлений на выходе ступеней адиабатического сжатия
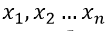 при котором затраченная на адиабатическое сжатие энергия
при котором затраченная на адиабатическое сжатие энергия 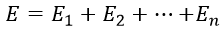 , минимальна;
, минимальна;2. Увеличение числа ступеней сжатия только на единицу позволяет сэкономить почти 16 % энергии, затраченной на адиабатическое сжатие газа в многоступенчатом компрессоре.
Ссылки:
1. Компрессоры газотурбинных установок (ГТУ).
2. Многоступенчатый компрессор.
3. Фан — Лянь — Цэнь, Ван, Чу – Сен. Дискретный принцип максимума. — М, «Мир»,1967.-176 с.
Комментарии (7)

Andy_U
27.01.2018 16:26Нет. Смотрите сюда, где написано, что глобальные максимумы/минимумы ищутся c помощью:
Global (brute-force) optimization routines (e.g. basinhopping, differential_evolution)
А minimize использует (см. Вашу же ссылку)
one of BFGS, L-BFGS-B, SLSQP, depending if the problem has constraints or bounds.
которые используют (численно вычисляемые) градиенты, якобианы и пр., т.е. ищут локальные максимумы/минимумы.
Другое дело, что могут быть посторонние соображения, что минимум/максимум в задаче единственный, или что начальное положение близко к глобальному экстремуму.
Scorobey Автор
27.01.2018 16:48Диапазон давлений задан -1-64.
Стартовые точки поиска x0 заданы.
Целевая функция этим ограничена и не имеет разрывов.
В указанных условия возможен только один минимум
при числовом методе его поиска !!!..

alkneu
27.01.2018 16:59Во 2ой ссылке дано аналитическое решение, дающее глобальный минимум:
x(i+1) = x(i) * c, где с = (P_конечное / P_начальное) ^ (1/n) (краевые условия x(0) = P_начальное, x(n) = P_конечное).
Доказывается в несколько строк (от противного):
Заметим, что надо минимизировать E = T * ( (x(1) / x(0) — 1) + (x(2) / x(1) — 1) +… + (x(n) / x(n-1) — 1), где T = m * R * T * gammma / (gamma -1) не зависит от x, т.е. достаточно искать минимум F(x) = x(1) / x(0) + x(2) / x(1) +… + x(n) / x(n-1)
Пусть x(0), x(1),…, x(n) — оптимальный набор
Если существует i: sqrt(x(i) * x(i+2)) != x(i+1), то набор
x(0), x(1),…, x(i), sqrt(x(i) * x(i+2)), x(i+2),… x(n) выгоднее, чем
x(0), x(1),…, x(i), x(i+1), x(i+2),… x(n) (что является противоречием).
Почему выгоднее? Потому что выражение y/A + B/y >= 2*sqrt(y/A * B/y) = 2sqrt(A*B) достигает минимума при y = sqrt(A * B) (здесь A = x(i), y = x(i+1), B=x(i+2)).
Т.е. в оптимальном решении sqrt(x(i) * x(i+2)) == x(i+1), или же x(i+1)/x(i) == x(i+2)/x(i+1).
Непонятно, зачем автор впихнул сюда scipy и зачем ему (или злому модеру) было тереть предыдущий мой комент.
Andy_U
27.01.2018 17:19Ага, тоже только что в Maple проверил. Надо бы еще проверить, не может ли эта величина c формально быть отрицательной при четном/нечетном количестве ступеней? Чтобы последовательность давления была типа +2, -4, +8, -16… А что, автор же unconstrained минимизацию использует? :)

alkneu
27.01.2018 17:25Даже проще: F(x) = x(1) / x(0) + x(2)/x(1) +… + x(n) / x(n-1) >=
n * ( (x(1) / x(0)) * (x(2) / x(1)) *… * (x(n) / x(n-1)) ^ (1/n) = n * (x(n) / x(0)) ^ (1/n)
(среднее арифметическое >= среднее геометрическое)
Равенство и минимум при x(1)/x(0) = x(2)/x(1) =… = x(n) / x(n-1).


Andy_U
Вы уверены, что нашли глобальные минимумы?
Scorobey Автор
Unconstrained minimization docs.scipy.org/doc/scipy-0.18.1/reference/generated/scipy.optimize.minimize.html