Как мы определяем глубину — расстояние от нашего местоположения до другого объекта? Для этого существует несколько способов, и один из самых распространённых и простых для понимания включает в себя такое геометрическое явление, как параллакс. Этот чрезвычайно простой принцип используется нашими глазами и мозгом для формирования нашего трёхмерного изображения мира, а астрономы столетиями используют его для определения расстояний (или относительных расстояний) от Земли до астрономических объектов.

Ещё один распространённый способ определять расстояния включает в себя отправку волны (звука, света, чего-то ещё), распространяющейся с известной скоростью, которая отражается от объекта и возвращается к нам; время, затраченное на возврат волны — эхо — сообщает нам расстояние до объекта. По этому принципу летучие мыши определяют расстояние до пищи и препятствий, а также работает радар.


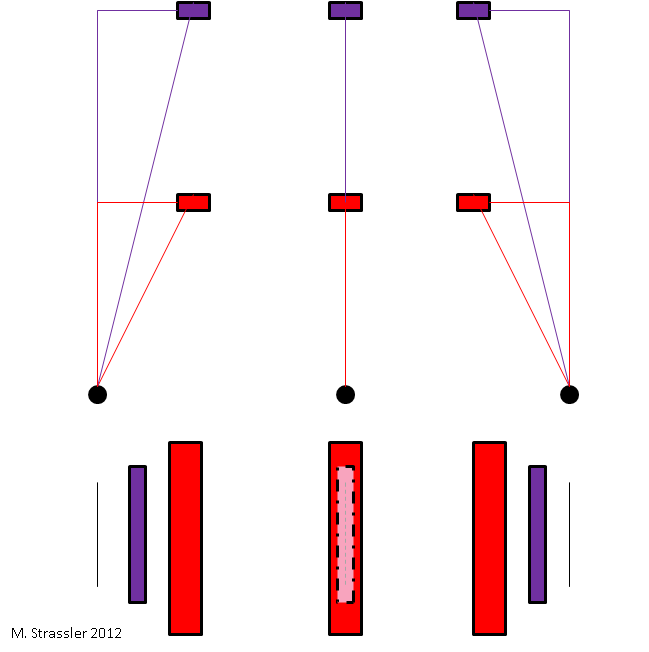
Рис. 1

Мы воспринимаем параллакс, даже не думая о нём, каждый раз, когда двигаем головой. Представьте, что произойдёт, Если ваш друг спрячется от вас, встав в нескольких метрах за крупным деревом (рис. 1, в центре). Если вы достаточно далеко отодвинетесь влево или вправо, вашего друга станет видно (рис. 1, слева и справа). Мы знаем, что всё дело просто в перспективе; при определённом угле зрения дерево уже не будет загораживать вам вашего таинственного друга. Геометрически происходящее изображено на рис. 1. Когда вы двигаетесь влево и вправо, смотря вперёд, близлежащие объекты меняют свой угол по отношению к тому, что находится прямо перед вами, быстрее, чем объекты, расположенные дальше. Из скорости изменения угла при вашем движении — из параллакса движения — вы можете понять, насколько далеко расположен объект.

Каждый ребёнок это знает, поскольку, когда вы выглядываете из окна движущейся машины, фонарные столбы проносятся мимо очень быстро, удалённые здания проходят медленнее, а Луна, находящаяся настолько далеко, что угол зрения по отношению к наблюдателю не меняется на ощутимую величину, пока машина едет по шоссе, как будто бы двигается вместе с машиной. Именно небольшой параллакс, являющийся следствием огромного расстояния, заставляет луну «следовать за машиной».

Все, кто смотрел старые двумерные мультфильмы (и многие современные), такие, как Флинстоуны, знают, что этот факт используется, чтобы изобразить глубину. Когда персонажи путешествуют в автомобиле, двигаясь слева направо, автомобиль рисуют неподвижным, деревья рисуют в другом слое, который с высокой скоростью передвигается справа налево, а холмы в удалении рисуют на третьем слое, который двигается справа налево чуть медленнее (см. рис. 2).


Рис. 2

Наша способность воспринимать глубину, даже не двигая головой, основана на том же принципе. Левый и правый глаз видят мир с немного разных углов. Попробуйте разместить пару объектов — неважно, каких, пусть даже это будут большие пальцы рук — так, чтобы один из них был в два раза дальше другого, и находился прямо за ним. Закройте левый глаз и посмотрите на них правым; затем поменяйте глаза; потом снова поменяйте, и сделайте так несколько раз — и вы увидите, что объекты двигаются, как на рис. 1, только ваш левый глаз увидит ближайший объект справа от того, что дальше, а правый глаз увидит его чуть левее.

Так почему вы воспринимаете эти объекты при помощи обоих глаз так, будто они находятся один за другим? У вашей оптической системы есть очень хитрый обработчик информации — своего рода компьютер. Для вас он создаёт не такую картину мира, какую непосредственно видят ваши глаза, а выстроенную на её основе при помощи сложных преобразований картину. Воспринимать глубину вам позволяет информация, полученная от двух глаз и скомбинированная вместе (это в основном — хотя параллакс движения тоже вносит свою лепту). Ни один из ваших глаз не может определить глубину, если вы стоите неподвижно. Попробуйте закрыть глаза, повернуться в другую сторону и открыть один глаз. Можете ли вы точно описать расстояние до предметов? Мир выглядит более плоским, более двумерным, чем обычно. С обоими открытыми глазами у вас нет таких проблем. Это использование двух изображений для использования трёхмерной карты мира называется стереоэффектом.

Но даже с одним открытым глазом вы можете довольно быстро оценить глубину, если подвигаете головой. Ваш мозг способен использовать параллакс движения — более быстрое изменение угла зрения на близлежащие объекты по отношению к отдалённым при движении влево или вправо — чтобы помочь восстановить часть информации о глубине, которая обычно получается сравнением вида из двух разных глаз (рис. 2).


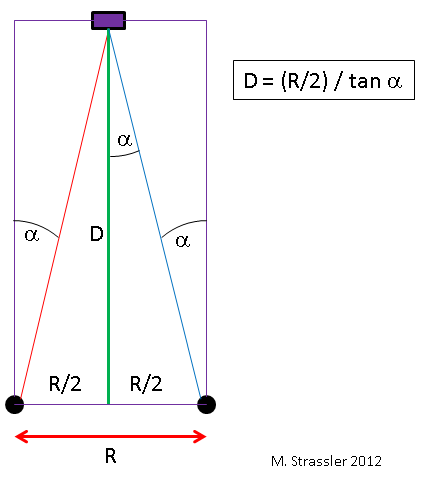
Рис. 3

Какие основные подсчёты использует наша оптическая система? Простейший случай показан на рис. 3. Допустим, объект находится прямо перед вами. Если ваши глаза находятся на расстоянии R друг от друга, а ваш левый глаз видит объект под углом ? правее по отношению ко взгляду прямо вперёд, а правый глаз видит объект под углом ? левее, тогда согласно простейшей геометрии прямоугольных треугольников, расстояние D до объекта будет равняться

$$

Из формулы видно, что когда D меньше, угол, на который линия взгляда на объект отстоит от прямого взгляда, становится больше. Именно этого мы и ожидаем от параллакса.

В более общем случае, показанном на рис. 4, когда объект находится не прямо перед вами, получается чуть более сложным, как и тригонометрические формулы, но в нём работает тот же самый основной принцип и в итоге его не так уж сложно подсчитать. Ваш мозг проделывает такие подсчёты так быстро (используя технику, которую мы пока ещё не раскрыли), что вы об этом и не подозреваете.

Для достаточно удалённых объектов угол ? оказывается слишком малым для того, чтобы его восприняли ваши глаза и мозг. В этот момент ваше чувство глубины пропадает. Поэтому Луна не кажется расположенной ближе, чем звёзды; они находятся слишком далеко, чтобы ощутить глубину. Также вашего ощущения глубины обычно не хватает, чтобы понять, пройдёт ли самолёт перед или за горой вдалеке. Но это просто ограничение ваших глаз.


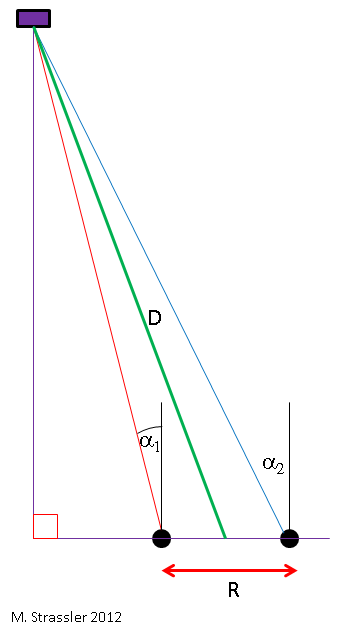
Рис. 4

Как определить расстояние до более удалённых объектов? Есть два варианта; разработать научный инструмент, способный измерять углы точнее, чем ваш глаз; увеличить R, чтобы сравнивать не вид из глаз, а, например, вид из двух камер, стоящих в нескольких метрах друг от друга, или даже в разных местах континента. А когда астрономы хотят измерить самые большие расстояния, какие только можно измерить при помощи параллакса, они сравнивают изображения удалённой звезды, сделанные с разницей в шесть месяцев, чтобы получить максимальное расстояние R на основании того, что Земля в течение года проходит довольно большое расстояние. Детали этих техник отличаются, но основной принцип тот же, что показа на рис. 3 и рис. 4 — принцип параллакса.