Полная классификация может привести к появлению большого количества новых материалов и технологий. Однако самые экзотические фазы продолжают сопротивляться пониманию учёных

За три последних десятилетия специалисты по физике конденсированных состояний открыли целую чудесную страну новых, экзотических фаз материи: внезапно появляющихся коллективных состояний взаимодействующих частиц, совсем не похожих на твёрдое, жидкое или газообразное состояния вещества, известные всем.

Эти фазы, как некоторые поняли в лабораториях, а некоторые – на основе теоретических расчётов, появляются, когда материя охлаждается почти до температуры абсолютного нуля, что больше чем на две сотни градусов ниже точки замерзания воды в обычных условиях. В этих холодных условиях частицы могут взаимодействовать такими способами, которые заставляют их отбросить все следы их прежней идентичности. Эксперименты 1980-х открыли, что в некоторых ситуациях электроны разделяются на фракции частиц, способных оставлять следы в пространстве-времени в виде косичек; в других среди них появляются безмассовые версии их самих. Решётка из вращающихся атомов становится жидкостью из закручивающихся петель или ветвящихся струн; кристаллы, которые изначально не проводили электричество, начинают пропускать ток по поверхности. Одна из фаз, шокировавших экспертов, когда её возможность впервые доказали математически в 2011 году, включает в себя очень странные сущности, "фрактоны", сцепляющиеся друг с другом в фрактальные узоры [согласно Вики, фрактоны – это фрактальный аналог фононов, квантов колебательного движения атомов кристалла / прим. перев.].

Теперь исследовательские группы из Microsoft и других компаний соревнуются в попытках записать квантовую информацию в косичках и петлях некоторых из этих фаз с целью разработки квантового компьютера. Тем временем, теоретики физики конденсированных состояний (КС) в последнее время провели несколько исследований, важнейших для понимания схемы коллективного поведения, с тем, чтобы пронумеровать и классифицировать все возможные фазы материи. Если у них получится составить полную классификацию, она не только позволит описать все виденные по сию пору фазы материи в природе, но и потенциально указать путь к получению новых материалов и технологий.

Исследователи под руководством десятков лучших теоретиков и с помощью математиков уже классифицировали целый вагон фаз, способных проявляться в одном или двух пространственных измерениях, связав их с топологией: с математикой, описывающей неизменные свойства таких форм, как сфера или тор. Они также углубились в джунгли фаз, возникающих в районе абсолютного нуля в трёхмерной материи.


Си Чен, теоретик физики конденсированных состояний из Калифорнийского технологического института

Учёные ищут «не какой-то определённый закон физики», — сказал Майкл Залетел [Michael Zaletel], теоретик ФКС из Принстонского университета. «Они ищут пространство всех возможностей, и это в каком-то смысле более глубокая и красивая идея». Это, возможно, и неожиданно, но, как говорит Залетел, пространство всех непротиворечивых фаз само по себе является математическим объектом «с невероятно богатой структурой, которая, как мы полагаем, в одномерном и двумерном мире один в один совпадёт с этими прекрасными топологическими структурами».

На ландшафте всех фаз существует «экономика вариантов», — сказал Ашвин Вишванат [Ashvin Vishwanath] из Гаврвардского университета. «И всё это кажется познаваемым» – такая удача его озадачивает. Нумерация фаз материи могла оказаться чем-то «вроде коллекционирования марок, — сказал Вишванат, — каждая немного отличается от других, и между ними нет никакой связи». Вместо этого классификация фаз больше похожа на «периодическую таблицу. В ней множество элементов, но они разбиваются на категории и мы можем понять эти категории».

Классификация проявляющегося поведения частиц может казаться не такой фундаментальной, но некоторые эксперты, например, Си-Ганг Вен [Xiao-Gang Wen] из Массачусетского технологического института, говорят, что новые правила проявляющихся фаз показывают, как сами элементарные частицы могут возникать на фоне лежащей в их основе сети запутанных битов квантовой информации, которую Вен называет «океаном кубитов». К примеру, у фазы "струнно-сетевая жидкость", способной проявляться в трёхмерной системе кубитов, возмущения выглядят точно так, как известные элементарные частицы. «Реальный электрон и реальный протон могут быть всего лишь флуктуациями струнной сети», — говорит Вен.

Новый топологический порядок

До того, как эти фазы при нулевой температуре неожиданно объявились, физики считали, что все фазы им уже известны. К 1950-м годам они уже могли объяснить, что происходит, например, когда вода превращается в лёд, описывая это как нарушение симметрии: если у жидкой воды существует симметрия вращения на атомном уровне (она во всех направлениях одинаковая), то во льду молекулы H₂O заключены в столбцы и строчки.

Всё изменилось в 1982 году после открытия дробного квантового эффекта Холла, проявляющегося в ультрахолодном двумерном газе из электронов. Вещество в таком состоянии обладало проявляющимися частицами с зарядами в доли зарядов электрона, делавшими доли шагов в одностороннем обходе периметра системы. «При помощи симметрии уже было невозможно различать такие фазы», — сказал Вен.

Требовалась новая парадигма. В 1989 году Вен представил, что такие фазы, как состояние дробного квантового эффекта Холла, проявляются не на плоскости, а на других топологических множествах – связанных поверхностях вроде поверхности сферы или тора. Топология относится к глобальным, неизменным свойствам таких пространств, которые нельзя поменять локальной деформацией. Как известно, по крайней мере, топологам, можно превратить пончик в чашку, деформировав его поверхность, поскольку у обеих фигур одно отверстие, а, следовательно, они топологически эквивалентны. Но растягивайте и сжимайте сколько угодно, а даже самый гибкий пончик никак не получится превратить в крендель.

Вен обнаружил, что в новых топологических условиях появляются у фаз нулевой температуры появляются новые свойства, и придумал термин "топологический порядок", описывающий суть этих фаз. Другие теоретики тоже открывали связь фаз и топологии. С открытием множества различных экзотических фаз – их уже известно так много, что, как говорят исследователи, они едва поспевают их описывать – стало понятно, что топология и симметрия предлагают неплохую систему для их организации.

Топологические фазы проявляются только в районе абсолютного нуля, поскольку только при таких низких температурах системы частиц могут приходить в основное квантовое состояние с наименьшей энергией. В основном состоянии деликатные взаимодействия, устанавливающие идентичность частиц – исчезающие при высоких температурах – связывают частицы в глобальные системы при помощи квантовой запутанности. Вместо того, чтобы описывать частицы индивидуально, математически они становятся компонентами более сложной функции, описывающей их всех разом, часто с появлением новых частиц в виде возбуждений глобальной фазы. Появляющиеся схемы дальнодействующей запутанности оказываются топологическими, то есть, нечувствительными к локальным возмущениям – как количество отверстий в множестве.


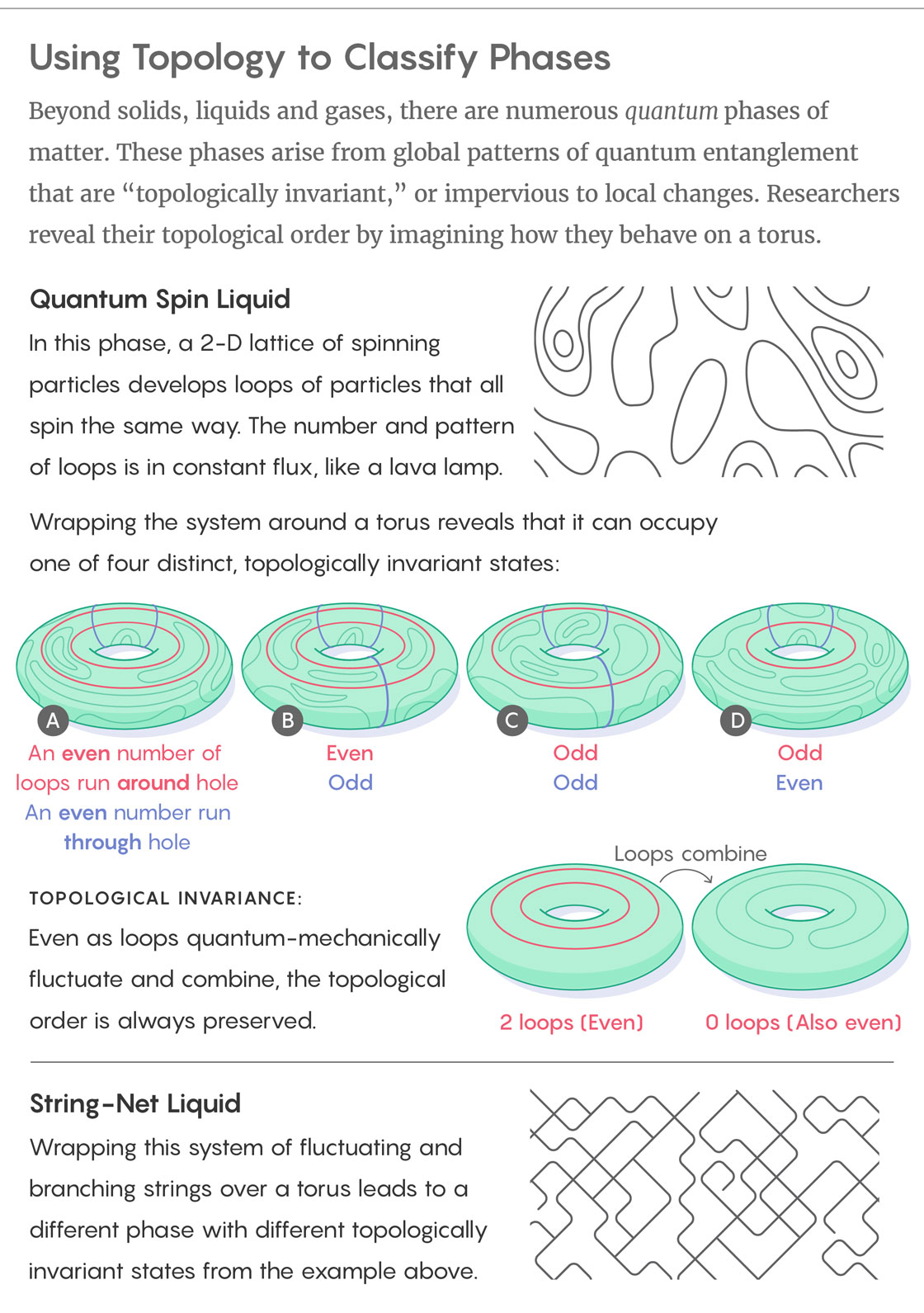
Вверху: фаза жидкости квантовых спинов. В этой фазе двумерная решётка вращающихся частиц приводит к появлению петель из частиц, вращающихся одинаково. Количество и расположение петель всё время меняются, и всё это напоминает лавовую лампу.

Если накрутить эту систему на тор, окажется, что она может занимать четыре различных, топологически инвариантных состояния:
A) Вокруг отверстия: чётное число петель / Сквозь отверстие: чётное число петель.
B) Чётное / нечётное.
C) Нечётное / нечётное.
D) Нечётное / чётное.

Несмотря на то, что петли постоянно испытывают квантово-механическую флуктуацию, топологический порядок всегда сохраняется (2 петли могут перейти в 0 петель, что тоже чётное число).

Внизу: струнно-сетевая жидкость. Если обернуть системой меняющихся и ветвящихся струн тор, то мы тоже получим различные топологически инвариантные состояния.

Рассмотрим простейшую топологическую фазу системы под названием «жидкость квантовых спинов», состоящую из двумерной решётки спинов, или частиц, указывающих вверх, вниз, или, с какой-то вероятностью, одновременно в обе стороны. При нулевой температуре спин-жидкость порождает струны спинов, указывающих в одном направлении, вниз, и эти струны формируют замкнутые петли. Направление спинов подвержено квантово-механической флуктуации, и узор из петель на материале тоже меняется: петли нижних спинов объединяются в более крупные петли или разделяются на более мелкие. В такой фазе жидкости квантовых спинов основное состояние системы – это квантовая суперпозиция всех возможных узоров петель.

Чтобы понять, почему эта схема запутанности представляет собой топологический порядок, представьте, как это делал Вен, что жидкость квантовых спинов разливается по поверхности тора, и некоторые из петель закручиваются вокруг его отверстия. Из-за этого вместо того, чтобы получить одно основное состояние, связанное с суперпозицией всех узоров петель, спин-жидкость будет существовать в одном из четырёх различных основных состояний, связанных с четырьмя суперпозициями узоров из петель. Одно состояние состоит из всех возможных узоров петель с чётным количеством петель, окружающих отверстие тора, и с чётным количеством петель, проходящих сквозь него. У другого первое число чётное, а второе нечётное; у третьего и четвёртого эти числа, соответственно, нечётное/чётное и нечётное/нечётное.

И попав в одно из этих состояний, система в нём и остаётся, несмотря на то, что узор петель локально всё время меняется. Если, к примеру, у спин-жидкости будет чётное число петель, окружающих отверстие тора, то две этих петли могут соприкоснуться и объединиться, и внезапно превратиться в петлю, которая вообще не окружает отверстие. Количество петель уменьшается на два, но всё равно остаётся чётным. Основное состояние системы – это топологически инвариантное свойство, устойчивое к локальным изменениям.

Квантовые компьютеры будущего могут воспользоваться этой инвариантностью. Если у вас будет четыре топологических основных состояния, не зависящих от локальных возмущений или ошибок, «у вас появиться способ хранения квантовой информации, поскольку ваш бит может означать, в каком состоянии вы находитесь», — объясняет Залетел, изучавший топологический свойства спин-жидкостей и других квантовых фаз. Таким системам, как спин-жидкость, не нужно оборачиваться вокруг тора, чтобы иметь топологически защищённые основные состояния. Любимой песочницей исследователей служит "тороидальный код", фаза, теоретически построенная теоретиком ФКС Алексеем Китаевым из Калифорнийского технологического института в 1997 году, и продемонстрированная в экспериментах за последние десять лет. Тороидальный код может существовать на плоскости и всё равно поддерживать несколько основных состояний, присущих поверхности тора. По сути, петли спинов способны сдвигаться с одного края системы и появляться на другом краю, и закрученные вокруг системы петли получаются эквивалентными петлям вокруг отверстия тора. «Мы знаем, как строить связи между свойствами основных состояний системы на торе и соответствующим поведением частиц», — сказал Залетел.

Спин-жидкости могут находиться и в других фазах, в которых спины не формируют замкнутые петли, а ветвятся и образуют сети струн. Это струнно-сетевая жидкая фаза, которая, согласно Вену, «может выдать всю Стандартную модель» физики частиц, начав с трёхмерного океана кубитов.

Вселенная фаз

Исследования, проведённые несколькими группами в 2009 и 2010 годах, закончили классификацию «обособленных» фаз материи, формирующихся в одном измерении – цепочек частиц. Обособленная фаза находится в основном состоянии: это состояние с низкой энергией достаточно далеко отстоит от состояний с высокой энергией, чтобы система стабильно успокаивалась в таком состоянии. Только у обособленных квантовых фаз возникают хорошо определённые возбуждения в виде частиц. Неотделённые фазы – это бурлящие квантовые супы, их свойства по большей части остаются неизученными.

Для одномерной цепочки бозонов – частиц вроде фотонов, с целым квантовым спином (что означает, что они возвращаются в изначальное состояние после того, как поменяются местами) существует только одна обособленная топологическая фаза. В этой фазе, впервые изученной теоретиком из Принстона Данканом Халдейном, получившим в 2016 году вместе с Дэйвидом Таулессом и Джоном Майклом Костерлицем нобелевскую премию за десятилетия работ по топологическим фазам, спиновая цепочка порождает частицы с полуцелым спином с обоих концов. У цепочки фермионов существует две обособленных топологических фазы (это частицы вроде электронов и кварков, с полуцелыми спинами – что означает, что при перемене позиций их состояние становится отрицательным). Топологический порядок в этих одномерных цепочках произрастает не из дальнодействующей запутанности, а из локальной симметрии, связывающей соседние частицы. Эти фазы называются «симметрично защищёнными топологическими фазами» и соответствуют «коциклам когомологических групп», математических объектов, связанных с такими инвариантами, как количество отверстий в множестве.


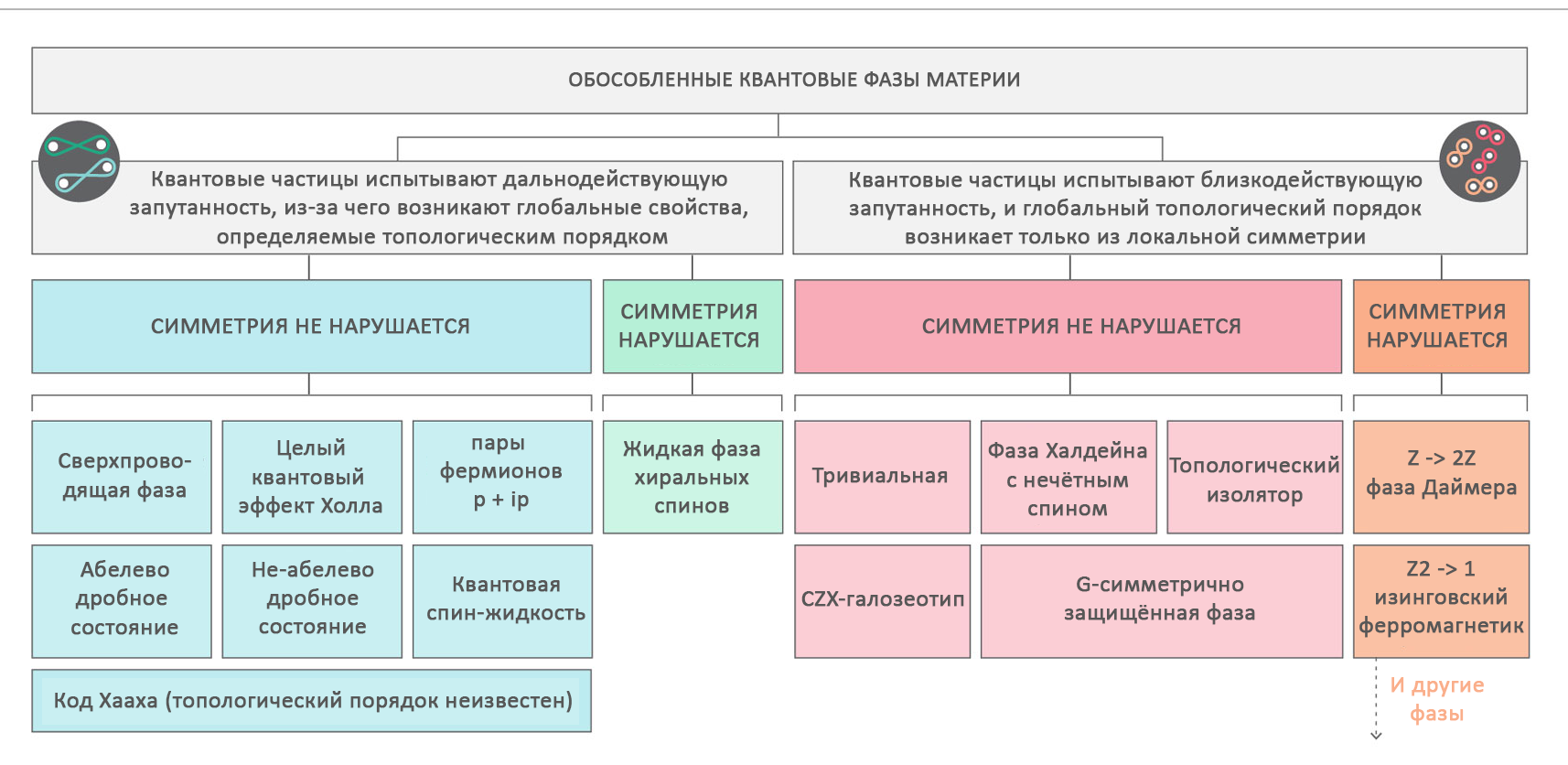
Периодическая таблица фаз: в таблице представлены характерные примеры обособленных фаз, со стабильным основным состоянием. Классификация считается полной для одномерных и двумерных пространств. Для трёхмерных пространств пока мало что известно.

Двумерных фаз гораздо больше и они гораздо интереснее. У них может проявляться то, что некоторые эксперты считают «истинным» топологическим порядком: порядком, связанным с дальнодействующей квантовой запутанностью, такой, как флуктуации петель в спин-жидкости. За последние несколько лет исследователи показали, что эти схемы запутанности соответствуют топологическим структурам под названием тензорные категории, нумерующим различные способы, которыми объекты могут сливаться и обвиваться вокруг друг друга. «Тензорные категории дают способ описать частицы, непротиворечиво сливающиеся и заплетающиеся в косы», — сказал Дэвид Перез-Гарсия из Мадридского университета Комплутенсе.

Исследователи, такие, как Перез-Гарсия, работают над математическим доказательством того, что известные классы двумерных обособленных топологических фаз полны. Он помогал закончить с одномерными классами в 2010-м, используя общепринятое мнение о том, что эти фазы всегда хорошо аппроксимируются квантовыми теориями поля – такими математическими описаниями, в которых окружающая среда, где существуют квантовые частицы, считается гладкой. «Эти тензорные категории гипотетически покрывают все двумерные фазы, но пока точного математического доказательства не существует, — сказал Перез-Гарсия. – Конечно, было бы гораздо интереснее, если бы можно было доказать, что это ещё не все фазы. Экзотические вещи всегда более интересные, поскольку в них есть новая физика, и они могут оказаться полезными».

Необособленные квантовые фазы представляют ещё одну область возможностей для изучения, но окутаны непроницаемым для большинства теоретических методов туманом. «На языке частиц говорить не получается, и мы начинаем сталкиваться с очень серьёзными трудностями», — говорит Сентил Тодадри [Senthil Todadri], теоретик КС из MIT. Необособленные фазы, например, служат главным препятствием на пути к пониманию высокотемпературной сверхпроводимости. Они затрудняют жизнь исследователям квантовой гравитации, примкнувшим к движению «всё из кубитов», считающим, что не только элементарные частицы, но и пространство-время, и гравитация появляются из-за схем запутанности, существующих в лежащем в основе всего океане кубитов. «Мы в „всё из кубитов“ проводим много времени в работе с необособленными состояниями, потому что именно оттуда появляется гравитация – по крайней мере, так мы считаем на текущий момент», — сказал Брайан Свингл, физик-теоретик из Мэрилендского университета. Некоторые исследователи пытаются использовать математический принцип двойственности для превращения картины квантового супа в эквивалентное описание частиц, сделанное в высшем измерении. «Это нужно расценивать как исследование новых территорий», — говорит Тодадри.

Ещё больший энтузиазм исследователей виден в трёхмерном пространстве. Пока что понятно, что когда спины и частицы освобождаются от оков двумерности и заполняют трёхмерное пространство реальности, начинают появляться непредставимо странные системы квантовой запутанности. «В трёх измерениях пока существуют вещи, ускользающие от тензорных категорий, — говорит Перез-Гарсия. – Возбуждение [полей] получается совершенно диким».

Код Хааха

И дичайшая из трёхмерных фаз появилась семь лет назад. Талантливый выпускник Калтеха Джионван Хаах [Jeongwan Haah] открыл её при помощи компьютерной симуляции, когда разыскивал «код мечты»: основное квантовое состояние, достаточно надёжное для того, чтобы безопасно хранить квантовую память даже при комнатной температуре.

Для этого Хааху пришлось обратиться к трём измерениям. В двумерных топологических фазах, вроде тороидального кода, значительную долю ошибок вносят «струновидные операторы»: возмущения в системе, приводящие к случайному формированию струн спинов. Эти струны иногда могут накрутить новые петли вокруг отверстия тора, изменяя количество петель с чётного на нечётное и наоборот, преобразовывая тороидальный код в одно из трёх других квантовых состояний. Поскольку струны растут неконтролируемо и оборачиваются вокруг всего остального, эксперты говорят, что в двумерном мире хорошую квантовую память построить невозможно.


Джионван Хаах

Хаах написал алгоритм поиска трёхмерных фаз, избегающий струновидных операторов. Компьютер выдал 17 точных решений, которые он затем проверил вручную. Подтвердилось, что четыре фазы свободны от струновидных операторов; одна из фаз с наибольшей симметрией стала известной, как код Хааха.

Код Хааха потенциально полезен для хранения квантовой памяти, но в то же время и ужасно странный. Сяо Чен, теоретик ФКС из Калтеха вспоминает, как услышала новости об этом, будучи аспирантом в 2011 году, через месяц-другой после сбивающего с толку открытия Хааха. «Все были шокированы, — говорит она. – Мы не знали, можем ли мы вообще с этим что-то сделать. И сегодня такая ситуация сохраняется уже много лет».

Код Хааха на бумаге довольно просто: это решение уравнения энергии с двумя членами, описывающие спины, взаимодействующие с восемью своими ближайшими соседями в кубической решётке. Но получающаяся фаза «напрягает наше воображение», — сказал Тодадри.

Особенностью кода являются частицеподобные сущности, фрактоны, которые, в отличие от петлевых рисунков в квантовой спин-жидкости, не жидкие, и покоятся на месте; фрактоны могут только перепрыгивать между своими позициями в решётке, если с этими позициями обращаться как с фрактальным рисунком. То есть, например, чтобы заставить фрактоны, стоящие в вершинах тетраэдра, поменяться местами, необходимо влить энергию в каждую вершину системы; но если увеличить масштаб, то окажется, что то, что мы считали вершиной, на самом деле оказывается четырьмя вершинами менее более мелкого тетраэдра, и нам приходится вливать энергию во все эти вершины тоже. Ещё увеличив масштаб, мы опять находим ещё более мелкий тетраэдр, и так далее. Такое фрактальное поведение означает, что код Хааха никогда не забывает стоящую в его основе решётку, и его нельзя аппроксимировать сглаженным описанием решётки, как это делается в квантовой теории поля. Более того, количество основных состояний кода Хааха растёт с размером лежащей в основании решётки – а это свойство точно не является топологическим (если растянуть тор, он всё-таки останется тором).

Квантовое состояние кода Хааха чрезвычайно стабильно, поскольку фрактальный оператор, идеально подходящий для него, вряд ли появится случайным образом. Эксперты говорят, что реализуемый вариант этого кода может иметь огромный интерес с точки зрения технологий.

Фаза Хааха породила всплеск теоретических рассуждений. Хаах помог с этим, когда в 2015 году с двумя коллегами из MIT открыл множество примеров в классе фаз, теперь известных, как «модели фрактонов», упрощённых родственников кода Хааха. Первую модель этого семейства представил Клаудио Чамон из Бостонского университета в 2005-м. Чен и другие учёные изучали топологию систем фрактонов, некоторые из которых позволяют частицам двигаться вдоль линий или плоскостей в трёхмерном пространстве, в результате чего могут помочь с концептуальным пониманием происходящего или могут быть более подходящими для экспериментальной реализации. «Это открывает нам путь ко множеству более экзотических вещей, — говорит Чен о коде Хааха. – Это демонстрация того, насколько мало мы знаем о трёхмерном мире и высших измерениях. И поскольку у нас пока нет системной картинки происходящего, нас ждёт много всяческих открытий».

Пока никто не знает, к какой части ландшафта возможных фаз принадлежат код Хааха и его родственники, или насколько большим может оказаться пространство возможностей. Согласно Тодадри, сообщество достигло прогресса в классификации простейших обособленных трёхмерных фаз, но до начала программы полной классификации нужно больше исследований. По его словам, ясно, что «когда мы осуществляем классификацию обособленных фаз материи в трёхмерном пространстве, нам придётся столкнуться с такими странными возможностями, одну из которых первым открыл Хаах».

Многие исследователи считают, что для описания фрактальной природы кода Хааха и открытия полного спектра возможностей трёхмерной квантовой материи могут понадобиться новые концепции классификации. Вен сказал: «Нужен новый тип теории, новое мышление». Возможно, сказал он, нам нужна новая картинка нежидких схем дальнодействующей запутанности. «У нас есть некие общие идеи, но систематической математики для их реализации нет, — сказал он. – У нас есть некое ощущение того, как это выглядит. А детальной систематизации не хватает. Но это и захватывает».