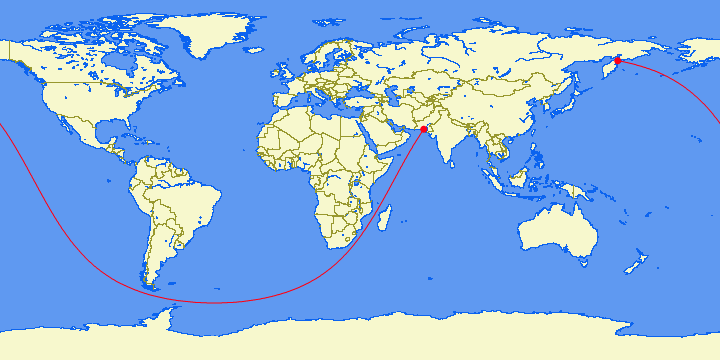
Иллюстрация Патрика Андерсона, на которой он в 2012 году предположил самый длинный возможный прямой маршрут по морю
В декабре 2012 года в подреддите /r/MapPorn разгорелась любопытная дискуссия. Один из пользователей под ником Kepleronlyknows (Патрик Андерсон) опубликовал изображение с картой мира, на котором изобразил прямой судоходный маршрут. Патрик высказал гипотезу, что это самый длинный прямой маршрут, который можно проложить по воде на нашей планете. Без единого поворота вы проплывёте по прямой около 32 000 километров, стартовав в районе Пакистана и финишировав на Камчатке. Абсолютно прямой маршрут проходит мимо Африки, Южной Америки и через Тихий океан до самой России.
Конечно же, автор произвёл расчёт по интуиции. Он предложил форумчанам проверить его гипотезу и найти более длинный маршрут, если таковой существует. Или попробовать доказать, что именно этот маршрут — самый прямой.
Сообщение вызвало бурные дебаты: сотни форумчан склонились над картами и глобусами. Главный вопрос — можно ли побить этот рекорд (UPD: примерно такие же дебаты развернулись в комментариях к этой статье на GT). Попутно возник ещё один вопрос: а какой самый длинный в мире маршрут по прямой по суше, а не по морю? То есть сколько можно идти по прямой, ни разу не наткнувшись на море.
Понятно, что результирующая кривая должна принадлежать большой окружности вокруг сферы земного шара (для простоты можно считать его сферой). Эта окружность соединяет точки на поверхности сферы по кратчайшему возможному пути. Но как найти эти окружности с верным решением?
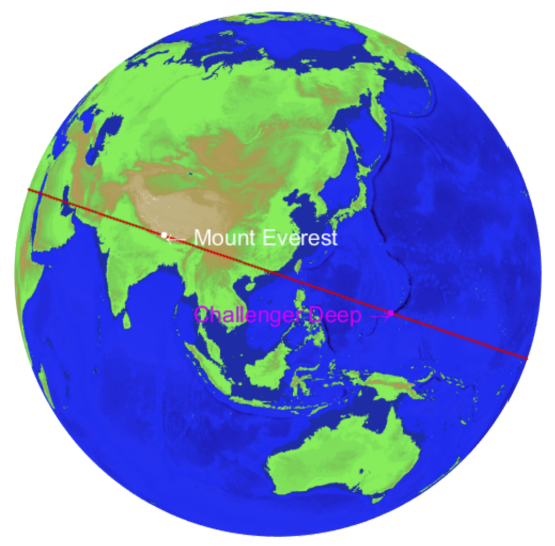
Окружность, которая соединяет самую высокую и самую низкую точки на поверхности Земли
Судя по всему, среди «горячих голов» на форуме Reddit нашлись-таки люди с фундаментальным образованием, которые основательно подошли к решению проблемы. Итак, ознакомьтесь с научной работой Рохана Чабуксвара (Rohan Chabukswar) из исследовательского центра United Technologies (Ирландия) и Кушала Мукерджи (Kushal Mukherjee) из научно-исследовательского подразделения IBM Research в Индии. Эти ребята разработали надёжный алгоритм для расчёта самого длинного прямолинейного пути на суше или на море. Научная статья опубликована 9 апреля 2018 года на сайте препринтов arXiv.og (arXiv:1804.07389v1).
Конечно, сразу приходит в голову решить задачу брутфорсом — перебрать все возможные окружности вдоль земной сферы. Но это слишком ресурсоёмкая задача: на карте мира с разрешением 1,85 км получится более 230 миллиардов таких окружностей. Каждая из них состоит из 21 600 отдельных пунктов, что составляет в общей сложности более пяти триллионов точек для расчёта.
Но Чабуксвар и Мукерджи разработали более быстрый метод на основе алгоритма, известного как метод ветвей и границ (branch and bound).
Метод ветвей и границ — общий алгоритмический метод для нахождения оптимальных решений различных задач оптимизации, особенно дискретной и комбинаторной оптимизации. По существу, метод является вариацией полного перебора с отсевом подмножеств допустимых решений, заведомо не содержащих оптимальных решений. Фактически, вместо оценки всех решений алгоритм проверяет одну ветвь за другой (аналог брутфорса). Но другой метод, называемый ограничением, значительно уменьшает область перебора. Каждая ветвь содержит подмножество потенциальных решений, одним из которых является оптимальное решение. Хитрость в том, чтобы найти свойство подмножеств, которое зависит от того, насколько близко решения подходят к оптимальному.
Такой вариант вычислений потребовал гораздо меньше вычислительных ресурсов: «Алгоритм вернул самый длинный путь примерно за 10 минут вычислений для водного пути и 45 минут вычислений для земного пути на стандартном ноутбуке», — говорят исследователи.
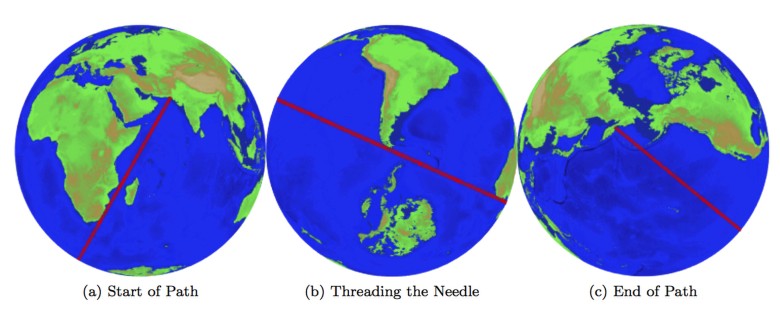
И оказалось, что Kepleronlyknows был совершенно прав. Самый длинный прямой водный путь начинается в городе Сонмиани, провинция Белуджистан, Пакистан, где находится ракетно-испытательный полигон. Маршрут проходит между Африкой и Мадагаскаром, а затем между Антарктидой и Огненной Землёй в Южной Америке — и заканчивается в Карагинском районе Камчатского края в России. Длина маршрута 32089 километров 700 метров.
Самый длинный путь по суше начинается близ городского уезда Цзиньцзян в провинции Фуцзянь, округ Цюаньчжоу (Китай). Он идёт через Монголию Казахстан, Россию и, наконец, достигает Европы, чтобы завершиться около города Сагреш в Португалии. В целом маршрут проходит через 15 стран и составляет 11241 километр 100 метров — более 101 градуса по земной окружности.
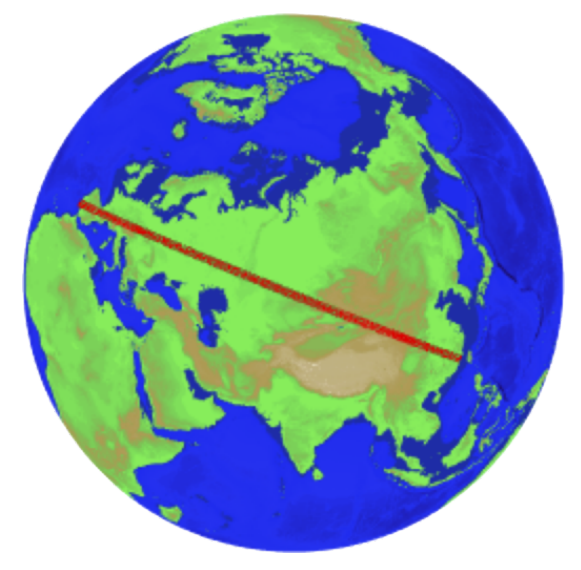
Через какие страны проходит самый длинный в мире прямой сухопутный маршрут:
- Китай (Цзиньцзян, 24°32'55'' N, 118°38'3'' E)
- Монголия
- Казахстан
- Россия
- Беларусь (три раза)
- Украина (два раза)
- Польша
- Чехия
- Германия
- Австрия
- Лихтенштейн
- Швейцария
- Франция
- Испания
- Португалия (Сагреш, 37°1'30'' N, 8°55'0'' W)
Если вам интересно, можете точно рассчитать, через какие конкретно города проходит рекордный в мире маршрут. Вдруг какой-нибудь сумасшедший путешественник решит пройти строго по прямой через всю Азию и Европу. Хотя, наверное, вопрос нужно ставить по-другому: кто первым это сделает и когда?
Комментарии (73)

juray
03.05.2018 22:07+2Без единого поворота и смены курса
Ну курс-то (то есть азимут направления) как раз постоянно корректировать придётся — дуга большого круга, не являющегося экватором или меридианом, пересекает разные меридианы под разными углами.
А линия постоянного курса — локсодрома — не является кратчайшим путём.
Alexklmn
03.05.2018 22:56Что-то вы все напутали. Курс нужно корректировать лишь если внешние факторы с него сбивают, поскольку это путешествие пока гипотетическое, то чисто теоретически ничто путешественнику не мешает. А в условии сказано, что путь прямой. У круга нет дуг какого бы он размера не был. Если идти не по компасу или звездам, то пофиг на меридианы. И вообще искали не кратчайший, а длиннейший путь.

alizar Автор
03.05.2018 23:16Курс судна — угол, в плоскости истинного горизонта, между носовой частью диаметральной плоскости судна и направлением на север.

Alexklmn
04.05.2018 01:23Да, точно. Оказывается.
Был уверен, что курсом называется угол между прямой проложеной из точки А до В и севером… а судно хоть боком, хоть задом идет вдоль этой прямой.
Zenitchik
04.05.2018 10:58+1Смотря что называть «прямой». Если геодезическую линию — то её угол к меридиану везде разный, если только она не совпадает с экватором или одним из меридианов.

juray
04.05.2018 14:34Ну, движение судна в условиях действия волн и ветра — отдельная песня. Курс от путевого угла и отличается-то из-за этих возмущений. Если ветра и течений нет — то совпадает (для моторного судна, парусное без ветра не движется).

juray
04.05.2018 14:26У круга нет дуг какого бы он размера не был.
Да, в математическом смысле, конечно, же, дуги бывают у окружности, а не у круга. Но в геодезии таки употребляют «большой круг» и «большая окружность» как синонимы. И термин «дуга большого круга» вполне существует.
искали не кратчайший, а длиннейший путь.
Ну, искали «самый длинный прямой маршрут», без определения, что значит «прямой» (только дальше по тексту — через два абзаца — становится понятно, что имеется в виду).
В полноценном стереометрическом смысле — линии, проведенные на земной поверхности прямыми быть не могут, из-за ее кривизны. Если соединить две точки земной поверхности прямой линией, она пройдёт «под землёй».
Поэтому возможны две трактовки:
1) прямой линией является картографическая проекция траектории.
2) «прямой» — в смысле таки кратчайший. И «длиннейший из кратчайших» не оксюморон — поскольку это две разные выборки — кратчайший выбирается из множества путей, соединяющий две фиксированные точки, а затем из длиннейший — из множества пар точек, расположенных на побережье.
А кратчайший маршрут между точками — это таки дуга большой окружности (то есть окружности, образованной пересечением земной сферы с плоскостью, проходящей через центр сферы). Что и указано в статье:Понятно, что результирующая кривая должна принадлежать большой окружности
Две точки на окружности разделяют ее на две дуги. Если не делить на сушу и воду, то из двух дуг кратчайшая только одна. Но в условиях это разделение есть, точки расположены на побережье, так что одна дуга будет кратчайшим водным путем, а другая — кратчайшим сухопутным.
И кстати, о проекциях. Есть такая проекция — меркаторовская, на ней меридианы изображены равномерно распределенными параллельными линиями. Если на ней провести прямую линию между двумя точками, то получим линию постоянного курса — локсодрому — удобную для навигации, но не кратчайшую.
А вот на гномонической проекции прямая линия как раз соответствует большой окружности. И в статье использована именно гномоническая.
Курс нужно корректировать лишь если внешние факторы с него сбивают, поскольку это путешествие пока гипотетическое, то чисто теоретически ничто путешественнику не мешает.
Согласен. В идеальной моделируемой ситуации, при отсутствии возмущающих факторов (и на идеальной сфере — и в задаче и так земную поверхность за сферу приняли) действительно движение будет само собой происходить по кратчайшей траектории, и смена курса будет происходить сама по себе. Но она таки будет происходить!

mayorovp
04.05.2018 09:21Да, курс будет меняться — но это не значит что его нужно корректировать, он будет прекрасно корректироваться сам по себе…

Zenitchik
04.05.2018 10:59Это в безвоздушном пространстве. В реальных же условиях курс необходимо постоянно поддерживать, и, соответственно, периодически вычислять его для своего нового местонахождения.

trapwalker
04.05.2018 12:30К черту курс. Зачем с компасами возиться, когда есть GPS Глонас. Просто будет цепочка точек и от точки к точке плывём потихонечку=)
Но в целом, конечно, я не спорю
Zenitchik
04.05.2018 14:20Зачем с компасами возиться, когда есть GPS Глонас
Прекрасно, он покажет Вам Ваше положение на глобусе. А направление движения от чего будете отсчитывать? Курс подкрался незаметно.

ScaryA
03.05.2018 22:11+1Есть такая книга: «Опрокинутый мир» Кристофера Приста, и если без спойлеров, в которой есть упоминание приблизительно этого маршрута. Но кроме этого момента, там есть много интересных идей, начиная с того, что там про город, который передвигается по рельсам. А вот для чего вся эта возня, читайте сами — там и математика и геометрия и всё это в антиутопии. Занятная книга для гика. Жаль только конец, на мой взгляд, как-то скомкан.

zagayevskiy
04.05.2018 12:44Да, конец полностью зафейлили. Такое ощущение, что автор не знал, что дальше делать, вот и придумал невнятный генератор, который выкидывает на помойку всю остальную книгу.

IDDQDesnik
03.05.2018 22:47+4

Revetements_Etales
03.05.2018 23:30arxiv.org/pdf/1804.07389v1.pdf, стр. 2
«Guy Bruneau of IT/GIS Consulting services calculated [5] a path from Eastern China to Western
Liberia as being the longest distance you can travel between two points in straight line without crossing any ocean or any major water bodies. However, the path crosses through the Dead Sea (which can be considered to be a major water body), and hence does not satisfy the constraints originally set out.»
IDDQDesnik
03.05.2018 23:42+1Тоесть Волгу пересекать можно, а Мертвое море (которое на самом деле озеро) — нельзя, ну ок.

wormball
04.05.2018 01:17yandex.ru/maps/?ll=70.305381%2C23.477941&z=4&rl=-10.95728674%2C6.51274340~130.60494131%2C18.91315047
Не пересекает мёртвое море! И даже ни одно озеро не пересекает, по крайней мере из тех, у которых есть название на яндексе. Суэцкий канал пересекает, но его в любом случае пришлось бы пересечь.
Houl777
04.05.2018 09:40Еще в Китае пересекает озеро. А вот Мертвое море, да, очень элегантно проходит вскользь.

wormball
04.05.2018 16:47Пересекает. Но у него даже названия не нарисовано! А вот маршрут из статьи пересекает, на минуточку, озёра Лак-дю-Бурже, Анси, Урнерзе, Валенсеэ, Штарнбергер-Зеэ, Дегтар, Бездрев, Басилецкы рыбник, Кардас, Вльцетинскы рыбник, Павовскы рыбник, Весельскы рыбник, Каменны рыбник, Став, Большое Песчанское, Ореховское, Завищанское, Червоное, Верхнеуральское вдхр., пруд Хрустальный, Кунайжарколь, Жарколь, Жасыбай, Сабандыколь, Каражырык, вдхр. Бухтарма, Бага-Нур.
yandex.ru/maps/?ll=118.485653%2C24.871142&z=9&rl=-8.91815977%2C37.02426436~127.53217010%2C-12.45737435&mode=search&text=37%C2%B01%2730%27%27%20N%2C%208%C2%B055%270%27%27%20W&sll=118.650568%2C25.046471&sspn=2.018738%2C1.058364
При таком раскладе упоминание мёртвого моря выглядит детсадовской отмазкой. Быть может, конечно, у них глобус точнее, нежели в яндексе, но вряд ли они смогли обойти все упомянутые озёра, даже исключая рыбники и водохранилища. По африканскому маршруту хотя бы пустыня львиную долю пути, и то мне пришлось приложить некоторые усилия, и всё равно одно озеро осталось.
И что характерно, до этого несчастного озера всё равно 12800 км получается. yandex.ru/maps/?ll=68.151056%2C41.301396&z=4&rl=-10.99093237%2C6.53197210~123.53078956%2C21.89867132

black_semargl
04.05.2018 03:16Я бы сухопутным маршрутом считал такой который можно пройти пешком не садясь ни на одно плавающее транспортное средство.
Т.е. мосты и тоннели через морские проливы тоже годны.
USBLexus
04.05.2018 03:46Т.е. мосты и тоннели через морские проливы тоже годны.
Тогда надо уточнять требования к «прямости» маршрута, в тоннель или мост еще попасть надо
Norno
04.05.2018 10:23Более того, туннель, как правило, еще и собственный изгиб имеет, и скорее всего ориентирован не в требуемом направлении. А вообще, конечно, требуется более точная постановка задачи (хотя, вероятно, в исходной статье, они есть, но я не пойду смотреть).

vorphalack
04.05.2018 06:27следующий шаг: «самый длинный реально осуществимый маршрут, имеющий смысл»

Squoworode
04.05.2018 08:49"Потому что могу" — это тоже смысл.

vorphalack
04.05.2018 09:42вы пропустили часть про «реально осуществимый». нарисовать 11ткм линейкой — вопрос нахождения крайних точек. но в чем смысл линии, если ее нельзя пройти?
у black_semargl идея вот уже более осуществимая, пожалуй, хотя и не до конца мне понятна мотивировка для такого похода.
MTyrz
04.05.2018 17:50вы пропустили часть про «реально осуществимый». нарисовать 11ткм линейкой — вопрос нахождения крайних точек. но в чем смысл линии, если ее нельзя пройти?
Жюль Верн. «Дети капитана Гранта».
Одна беда, не сухопутный, не морской — смешанный.

black_semargl
04.05.2018 09:13Обойти евразоафрику по берегу…

leggiermente
04.05.2018 12:13… и наткнуться на фракталы. Длина береговой линии стремится к бесконечности (см. Мандельброта)

Welran
04.05.2018 11:07Ну вообще можно идти до самой смерти и даже ни разу не пройти по одному месту два раза. Нужно уточнять что это самый длинный из маршрутов соединяющих две точки кратчайшим путём. Ну и если реально осуществимый то видимо есть возможность пользоваться самолётами и другим транспортом. А то путь от мыса Горн до мыса Доброй Надежды пешком не особо то и назовешь осуществимым.

PwrUsr
04.05.2018 12:35+1Суэцкий канал искуственный — так что его можно не считать… а если еще по льдам передвигатся — то сухопуткой можно с России в Америку попасть (кому-то это удавалось — сложно но можно)… А с Северной Америки в Южную тоже можно по суше (правда там болота — но теоритически можно).
Так что путь увеличивается где то от юга африки до юга Южной Америки :)
DonArmaturo
04.05.2018 13:47В детстве (в далекие 70-е) читал книгу автопутешественника из Анкориджа до Огненной Земли. По Тихоокеанскому побережью болота редкость, там больше горы.
Насчет каналов (Суэц, Панама) полностью согласен — руками сделано. А лед — естественное образование, ничуть не хуже сухопутного пути для Моисея :)

ibKpoxa
04.05.2018 16:03С северной в южную не получится, перешеек с изгибами.

PwrUsr
04.05.2018 17:45А при чем тут изгибы? Я в том плане, что если исключить реки (иначе вообще никуда не доберешься), и пользоватся мостами или естественными (лед) или искуственными, но не между материками, а только через каналы реки и т.п, то "пешком" в принципе из юга африки до юга южной америки — вполне можно добратся.

halted
04.05.2018 14:15+1Это же можно создать прямой железнодорожный путь, который логистически покроет основную часть материка.

zapimir
04.05.2018 14:38Там как бы гладко было на бумаге, да забыли про овраги :)
Не любой путь, который подойдет безбашенным установителям рекордов подождет для железной дороги.
Spaceoddity
04.05.2018 18:01Ну теоретически почему бы и нет? Вопрос же только в трудозатратах… Буквально на днях много читал про «северомуйский тоннель».

SinsI
04.05.2018 16:45Понятно, что результирующая кривая должна принадлежать большой окружности вокруг сферы земного шара
Не совсем верное утверждение.
Просто в данном исследовании под «прямым» маршрутом понимается именно маршрут, принадлежащий такой окружности.
Если же под «прямым» понимать, к примеру, и движение вдоль параллелей — то вполне возможны и более оптимальные маршруты.

silveruser
04.05.2018 23:56А мне из данной статьи другой факт любопытен: по результатам «флейма» на reddite-е Рохан Чабуксвара и Кушала Мукерджи написали научную работу, плюс программку для расчета, а на «хабре» 70 чуваков лишь ЧСВ померялись да «попетросянили» ;) Как говаривал Шрек из мультика:«Well, that explains a lot»…

Dootch
06.05.2018 04:02Бегло просмотрел статью, для определения где вода, а где суша они использовали глобальную модель рельефа ETOPO1. Модель похожа на карту высот. Авторы статьи решили так: если значение отрицательное — значит вода, если положительное — значит суша. Это строго говоря не так, ведь на Земле есть суша ниже уровня моря.
Кроме того, вычисления проводились исходя из предположения что земля это сфера. Хотя на таких масштабах я бы все же использовал аппроксимацию земной поверхности геоидом WGS84, что конечно по идее сильно усложнит математику ;)
Хотя мне кажется применение геоида может максимум сместить крайние точки маршрута на несколько сотен метров.



dmitryredkin
Ну да, как же, сухопутный! А реки???
ehxo
Ну как же по прямой? А горы?
vdonich
Я бы поставил вопрос так — каким максимальным отклонением от прямой можно пренебречь?
trapwalker
Минимальным=) Это вообще отдельные задачи — пройти этот «прямой» маршрут как можно прямее по разным метрикам:
— кратчайший по расстоянию;
— с минимальным отклонением в проекции на сечение;
— с минимальным средним (арифметическим, геометрическим и т.д.) отклонением в проекции на сечение;
— с минимальным интегральным отклонением по модулю;
— с минимальным амплитудным отклонением…
Это просто праздник какой-то для всяких любителей померяться количеством штампов в загран-паспорте. Эх,. я тоже любитель, но теоретический=)
General_Failure
По мостам? Пересечение реки по мосту же сухопуткой считается
(Интересно, а использование паромной переправы куда относится?)
Zenitchik
А в местах пересечения рек маршрутом мосты имеются?
trapwalker
Для пущего повышения «полезности» этой задачи можно попробовать все заборы учесть, хотя, наверно, паркурщики подтянутся… и перелезут.
Ой, да, задача хоть и бесполезная практически, но интересная и заставляет пораскинуть мозгами. Мне почему-то о разных специальных проекциях подумалось и о поиске диаметров многоугольников на плоскости.
agugnin
Ну если лететь самолетом, то можно и не отклоняться… если топлива хватит :)
yarric
11 тыс. км для 787 — пустяк.