
Приготовьтесь, вас ждёт крайне педантичная статья, которая вполне может спасти вас на собеседовании или сэкономить несколько часов при вылавливании бага в продакшне!
Я сейчас активно работаю над вторым сезоном «Руководства для самозванца» и пишу о шифре RSA для SSH, который, очевидно, является самым загружаемым фрагментом кода в истории IT.
Хочется полностью разобраться в этой истории. Кто придумал этот шифр, как он работает, почему работает и будет ли работать в будущем. Сейчас я раскопал одну чертовски интересную историю. Я не криптоманьяк и вижу, как других буквально засасывает в эту область. Но мне это тоже интересно, потому что повсюду есть маленькие норки, а меня как сороку привлекают блестящие штучки в глубоких норках. Я также очень хорош в метафорах.
В любом случае: на прошлой неделе я узнал что-то странное и хочу поделиться: оказывается, mod и остаток от деления — не одно и то же. Действительно забавно то, что некоторые читатели при этих словах выпрыгивают со своих кресел и орут: «А ведь именно это я всегда пытался сказать вам и всем остальным!»
Позовите ребят из секты «mod не остаток»! Это для вас.
Что такое mod?
Я должен был изучить это, как и в прошлый раз, когда всплыла такая тема. Это одна из тех вещей, которые ты знаешь, но не запоминаешь. Когда вы применяете mod, то делите одно число на другое и берёте остаток. Итак: 5 mod 2 будет 1, потому что 5/2=2 с остатком 1.
Термин mod означает операцию modulo, с модулем 2 в данном случае. Большинство языков программирования используют
% для обозначения такой операции: 5 % 2 = 1. Вот где мы попадаем в странную серую область.
Математика циферблата
Помню, как учил это в школе, а потом забыл. Существует тип математики, называемый «модульной арифметикой», которая имеет дело с циклическими структурами. Самый простой способ представить это — циферблат с циклом 12. Для математика циферблат — это
mod 12. Если хотите понять, можно ли равномерно разделить 253 часа на дни, то можете применить операцию 253 mod 24, результатом будет 13, поэтому ответ «нет»! Мы можем ответить «да» только если результат 0.Другой вопрос, который вы можете задать: «Если я выеду в 6 вечера, сколько времени будет по приезду через 16 часов?». Это будет
6 + 16 mod 12, то есть 10.Криптографы любят
mod, потому что при использовании с действительно большими числами можно создать нечто, известное как «односторонние функции». Это специальные функции, которые позволяют легко вычислить что-то в одном направлении, но не в обратном.Если я скажу вам, что 9 является результатом возведения в квадрат, вы можете легко определить, что на входе было 3. Перед вами весь процесс от начала до конца. Если я скажу, что 9 является результатом
mod 29, то будет сложнее понять, что на входе.Криптографам нравится эта идея, потому что они могут использовать деление с остатком с гигантскими простыми числами для генерации криптографических ключей. Это совсем другая история: если хотите прочитать об этом, то можете купить книгу или, ещё лучше, поддержать мои усилия написать её.
Впрочем, не будем отклоняться от темы.
Остатки и математика циферблата
Теперь переходим к сути: modulo и простой остаток одинаковы, когда числа положительны, но отличаются в случае отрицательных чисел.
Рассмотрим такую задачу:
const x = 19 % 12;
console.log(x);Каково значение
x? Делим числа и получаем 7 как остаток от 12. Это верный ответ. Как насчет такого:const y = 19 % -12;
console.log(y);Используя обычную математику, мы можем умножить -12 на -1, что даёт 12, и у нас по-прежнему остаётся 7, поэтому наш ответ снова 7.
JavaScript с этим согласен:
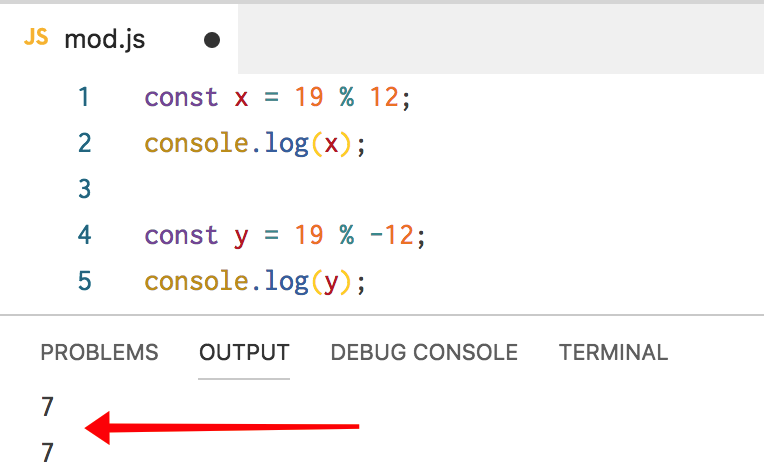
C# тоже согласен:
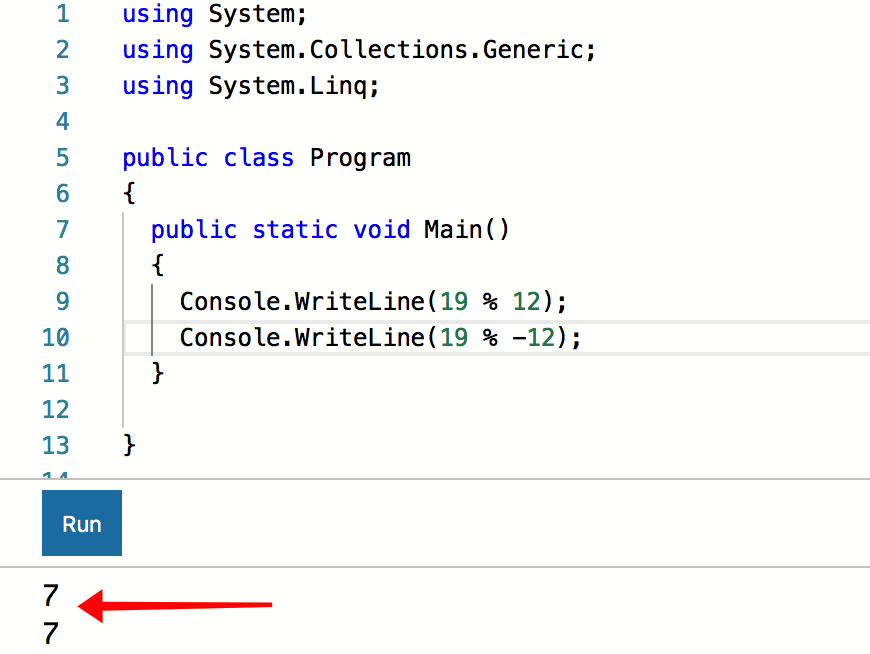
Google согласен с первым утверждением, но не согласен со вторым:
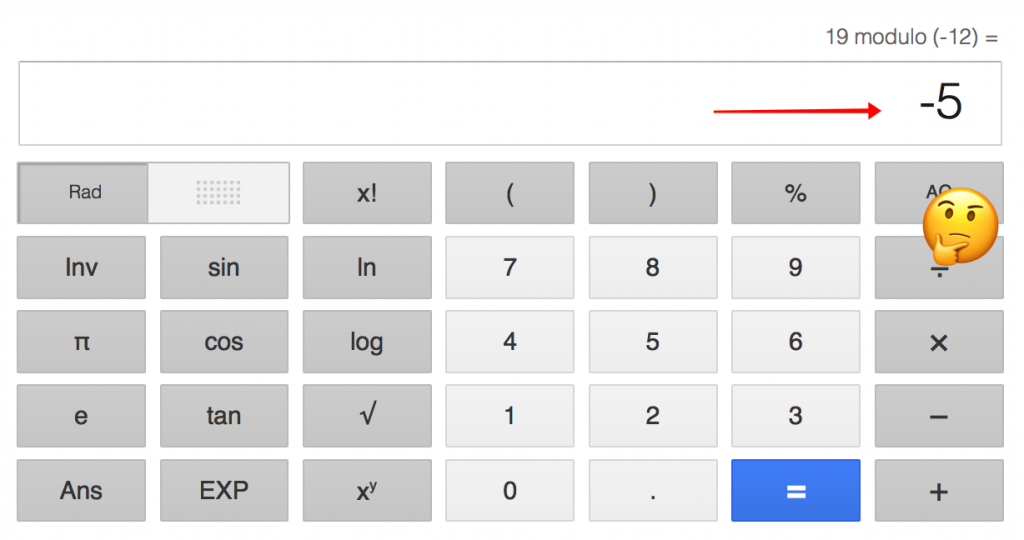
Ruby согласен с Google:

Во имя Дейкстры, что здесь происходит?
Вращение часов назад
Чтобы ответить на вопрос, следует понять разницу между остатком и modulo. Программисты объединяют эти операции, но не должны этого делать, потому что они дают одинаковый результат только в случае, если делитель (в нашем случае 12) положителен. Вы можете легко отправить баги в продакшн, если делитель отрицательный.
Но почему существует разница? Рассмотрим положительный делитель
19 mod 12 на часах: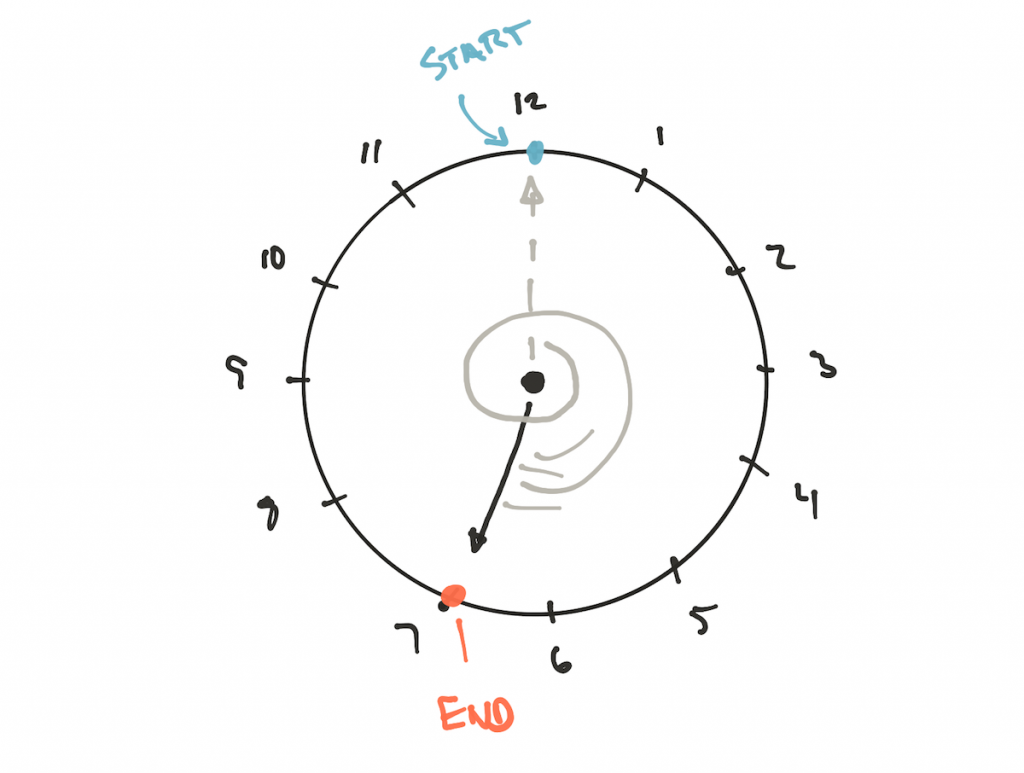
Конечный результат 7. Мы это знаем и мы можем доказать математически. Но что насчёт
19 mod -12? Здесь нужно использовать другие часы: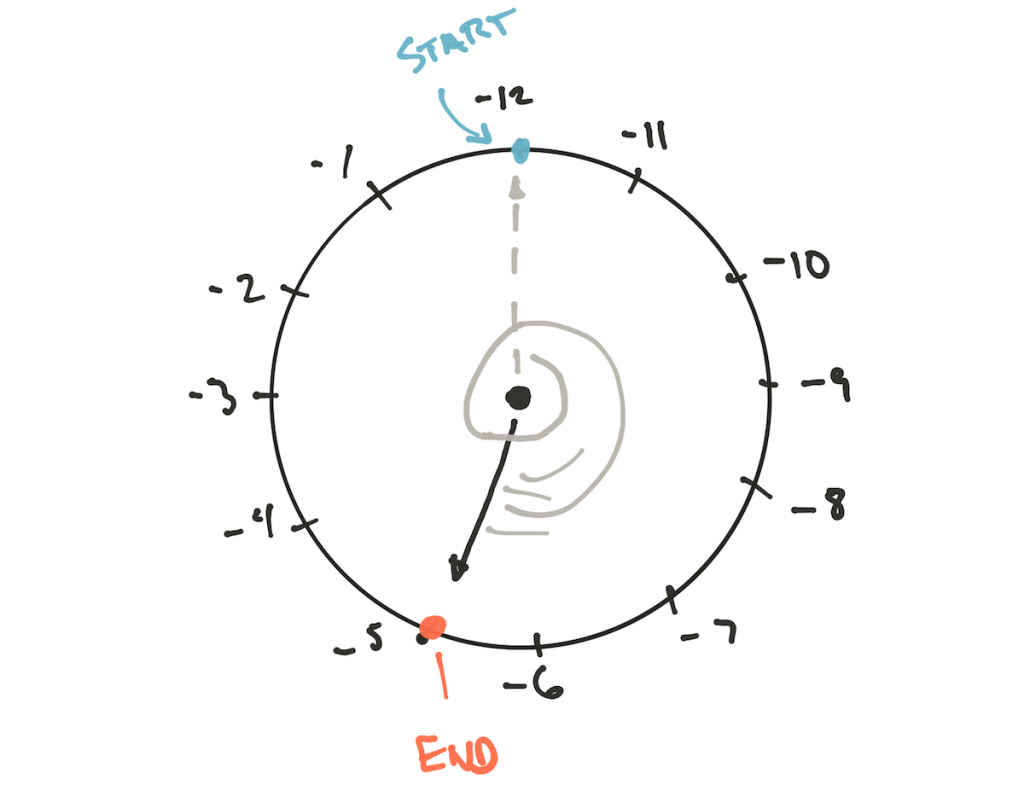
Модуль равен -12, и мы не можем игнорировать или изменить его, умножив на -1, поскольку модульная арифметика так не работает. Единственный способ правильно рассчитать результат — переставить метки на часах так, чтобы мы двигались от -12 или вращали часы против часовой стрелки, что даёт тот же результат.
Почему не начать метки с -1, двигаясь к -2, и т.д.? Потому что в таком случае мы будем двигаться назад и постоянно уменьшать результат, пока не достигнем -12, и в этот момент сделаем прыжок +12, а modulo так не работает.
Это известная вещь
Прежде чем назвать меня сумасшедшим и начать гуглить тему: это известный факт. На самом деле MDN (Mozilla Developer Network) даже дошла до того, чтобы назвать
% операцией «остатка» (remainder), а не modulo:Оператор remainder возвращает остаток от деления одного операнда на другой. Он всегда принимает знак делимого.
Вот что Эрик Липперт, один из богов C#, говорит о modulo в C#:
Однако это совсем не то, что оператор % реально делает в C#. Оператор % не является каноническим оператором modulus, это оператор остатка.
А как на вашем языке?
Ну и что?
Могу понять, если вы дочитали досюда, а теперь чешете голову и задаётесь вопросом, стоит ли беспокоиться. Думаю, что стоит по двум причинам:
- Я представляю, как этот вопрос займёт меня врасплох на собеседовании.
- Я представляю, как этот попадёт в продакшн, а разработчики будут несколько часов выяснять, почему математика не работает.
Это также забавный факт на случай, если рядом появится ваш педантичный друг-программист.
Комментарии (63)

ultrinfaern
24.08.2018 09:09Кстати, заметили ли вы что -5 (один ответ) и -7(другой) дают -12?
Если не привлекать циферблаты и куда крутить то можно объяснить так:
Классическое определение деления с остатком: a = b*q + r, где r — и есть остаток.
Для положительных чисел это формула тривиальна: b*q меньше a. А вот для отрицательных возникает вопрос — каким должен быть b*q — меньше? Так если меньше тогда абсолютное значение b*q больше, чем a и остаток всегда будет положительным.
Разные языки программирования\системы используют оба варианта реализации.
Doomsday_nxt
24.08.2018 09:34Просто в случае: a = b * q + r, при a = 19, b = -12, q может быть равно как -1 (тогда r = 7) так и -2 (тогда r = -5)

ainoneko
24.08.2018 09:50В классическом определении есть ещё вот это:
«На остаток налагается дополнительное условие: 0 <= r < |b| то есть остаток от деления должен быть неотрицательным числом и по абсолютной величине меньше делителя. „

anandr
24.08.2018 09:16Угу, после матлаба, где функция mod работает как учат в курсе математики долго не мог привыкнуть к поведению оператора % в C/C++.
Потому что C/C++ это так:
(x % y) = x — trunc(x/y)*y, а в математике принято так:
(x % y) = x — floor(x/y)*y.
Вот и приходится постоянно всюду дописывать свою функцию.
andreishe
24.08.2018 15:46В C++ (и в C) требуется чтобы выполнялось равенство
(a / b) * b + a % b = a. Я натыкался на различное поведение в разных компиляторах для отрицательных чисел.
Porohovnik
24.08.2018 18:29-2В равенстве где-то ошибка: после преобразования получилось:a + a % b =a-это значит что остаток всегда равен 0, а это неверно.

Mikluho
24.08.2018 09:24+1Очень полезное замечание.
И аналогия с циферблатом весьма наглядна. Мне, кстати, больше нравится идея крутить его в обратную сторону для отрицательного модуля.
Осталось только не забыть его к тому моменту, когда вдруг действительно потребуется вычислять modulo с отрицательным модулем.

vesper-bot
24.08.2018 09:50+1По мне, остаток от деления должен быть вообще всегда неотрицательным. Т.е. 19 mod 12 === 7, 19 mod (-12) === 7, (-19) mod 12 === 5. И никаких -5 или -7!

ainoneko
24.08.2018 09:53По мне, остаток от деления должен быть вообще всегда неотрицательным.
В математике это так же, а в программировании — как получится.

vesper-bot
24.08.2018 10:51Как я понимаю, началось с того, что в 8086 IDIV делил со знаком и пихал остаток тоже со знаком, возможно, так было проще разработать процессор. Потом в Си, чтобы упростить трансляцию на х86, разрешили x%y быть меньше нуля, и понеслась. stackoverflow.com/questions/49602476/intel-x86-can-idiv-yield-a-negative-remainder

valery1707
24.08.2018 10:42В Java:
public class ModuloTest { public static void main(String[] args) { System.out.println("19 % 12 = " + 19 % 12); System.out.println("19 % -12 = " + 19 % (-12)); } }
Будет вот так:
19 % 12 = 7 19 % -12 = 7

mark_ablov
24.08.2018 11:21> Если я скажу вам, что 9 является результатом возведения в квадрат, вы можете легко определить, что на входе было 3.
[зануда mode]
-3 в квадрате так же даст 9 ;)
[/зануда mode]
domix32
24.08.2018 15:46Два-три варианта лучше чем чем бесконечность.

Prototik
24.08.2018 22:23+1[зануда mode]
Бесконечность не помещается в фиксированное количество бит, так что не бесконечность.
[/зануда mode]
BD9
24.08.2018 22:47ru.wikipedia.org/wiki/IEEE_754-2008
Формат IEEE 754 представляет собой «совокупность представлений числовых значений и символов». Формат может также включать в себя способ кодирования.
Формат включает:
Числа
Положительный нуль +0 и отрицательный нуль -0.
Две бесконечности: +? и ??.
Два вида NaN
Prototik
24.08.2018 22:54+1Это, конечно, похвально, что вы знаете про IEEE 754. Но модуль (или остаток, называйте как хотите) не применим на эти бесконечности — результат NaN. В любом случае даже IEEE754 не может вместить в себя все возможные числа — с фиксированным числом бит это просто невозможно.

domix32
25.08.2018 15:50Если задаться целью то вполне можно реализовать генерацию чисел до того которого очень хочется. Только возникает вопрос зачем и готовы ли вы ждать бесконечность и предоставить бесконечное количество энергии? Думаю никто не доживет и первого десятка лет

geisha
24.08.2018 11:28Теперь переходим к сути: modulo и простой остаток одинаковы, когда числа положительны, но отличаются в случае отрицательных чисел.
Ну и ну. Мне казалось, что это даже на собеседованиях уже не спрашивают, а тут на хабре такой срыв покровов, прям целый перевод.

Neusser
24.08.2018 12:19Это будет
6 + 16 mod 12
Хоть в данном примере результат и не меняется, но все-таки(6 + 16) mod 12.

maslyaev
24.08.2018 12:20+1Питон:
>>> divmod(19, 12) (1, 7) >>> 19//12, 19%12 (1, 7) >>> divmod(19, -12) (-2, -5) >>> 19//-12, 19%-12 (-2, -5)

bormant
24.08.2018 13:00В Паскалях несколько иначе:
begin Writeln(19 mod 12:4, -19 mod -12:4, -19 mod 12:4, 19 mod -12:4) end.
7 7 -7 -7
vesper-bot
24.08.2018 17:59Скобки надо расставить для чистоты эксперимента. Хотя унарный минус объявлен как операция с высшим приоритетом, мало ли как расставляет приоритеты конкретный паскаль. Но -7 — как-то перебор.
Edit: пост от a-tk показывает, что этот паскаль взял в лоб idiv. Тогда нормально.

INCorpes
24.08.2018 13:00Так много написано, с кусками кода в картинках (что, как мне кажется, выглядит не очень красиво). А тем временем на википедии по ссылке отличное описание в один абзац, а ниже таблица с тем, как же берется остаток от деления в конкретном языке программирования.
В той же java вы можете использовать или так или эдак :)

kot_mapku3
24.08.2018 13:51Я помню как будучи ещё школьником мне об этом рассказывал профессор криптографии из МФТИ, когда он объяснял мне афинное шифрование. Я каждый раз впадал в эйфорию, когда мог разгадать(вычислить) очередной ключ!

a-tk
24.08.2018 15:15А вот что считает x86 в этой ситуации:
std::cout << m(19, 12) << std::endl; std::cout << m(19, -12) << std::endl; std::cout << m(-19, 12) << std::endl; std::cout << m(-19, -12) << std::endl;
Реализация:
int __cdecl m(int a, int b) { __asm { mov eax, a mov ebx, b cdq idiv ebx xchg eax, edx } }
Вывод: 7 7 -7 -7

michael_vostrikov
24.08.2018 19:34+119 % 12 - отложить вектор +12 +1 раз, остается 7 7 ------> .------------------> .-----------> 0 19 % -12 - отложить вектор -12 -1 раз, остается 7 7 ------> .------------------> .<----------- 0 -19 % 12 - отложить вектор +12 -1 раз, остается -7 -7 <------ <------------------. ----------->. 0 -19 % -12 - отложить вектор -12 1 раз, остается -7 -7 <------ <------------------. <-----------. 0
michael_vostrikov
25.08.2018 06:47+1А для модулей видимо получается так:
A всегда раньше по направлению, чем B. -19 % 12 19 % 12 5 7 ---->. ------> > > ----------->----------->----------->-----------> A B 0 A B -19 % -12 19 % -12 -7 -5 <------ .<---- < < <-----------<-----------<-----------<----------- B A 0 B A

BD9
24.08.2018 23:09+1Насколько я понимаю, речь идёт о построении кольца вычетов по некоторому натуральному модулю n, т.ч. отрицательные n не рассматриваются. Из колец вычетов можно получить поля вычетов. При n меньше единицы имеющаяся теория не работает, нужно строить другую (хотя, наверное, незачем). ПМСМ, автор исходной статьи просто плохо знаком с теорией.
В криптографии сравнения можно встретить в системах с открытым ключом, использующих, например, алгоритм RSA или протокол Диффи — Хеллмана. Также, модульная арифметика обеспечивает конечные поля, над которыми затем строятся эллиптические кривые, и используется в различных протоколах с симметричным ключом (AES, IDEA). (источник)

VladVR
24.08.2018 23:12Целочисленно делим 19 на -12, получаем -1.
Далее остаток от деления 19 — (-12 * -1) = 7
Тут все логично.
А что такое -5 я так и не понял, Очень похоже, что это действительно ошибка в процессоре, баг возведенный в ранг фичи.

Bitumok
25.08.2018 16:04Из курса "Основы программирования на Python" (Coursera):
Особо остановимся на операциях вычисления целой части и остатка от деления от числа.
Пусть заданы два числа A и B, причем B > 0. Обозначим за C целую часть от деления A на B, C = A // B, а за D — остаток от деления A на B, D = A % B.
Тогда должны выполняться следующие утверждения:
A = B ? C + D
0 ? D < B
Эти утверждения необходимы для понимания процесса взятия остатка от деления отрицательного числа на положительное. Нетрудно убедиться, что если -5 разделить на 2, то целая часть должна быть равна -3, а остаток равен 1.
В некоторых других языках программирования остатки в такой ситуации могут быть отрицательными, что неправильно по математическим определениям.
В случае, если B < 0 выполняются следующие утверждения:
A = B ? C + D
B < D ? 0
Например, при делении 11 на -5 мы получим целую часть равную -3, а остаток будет равен -4. Если же разделить -11 на -5, то целая часть будет равна 2, а остаток будет равен -1.
daexmach
25.08.2018 18:09В официальной документации объяснение лаконичнее:
Почему -22 // 10 (прим.: целочисленное деление) возвращает -3?
Это следствие того, что i % j (прим.: остаток от деления i на j) имеет тот же знак, что и j. Чтобы так было, а также выполнялось:
i == (i // j) * j + (i % j)
целочисленное деление должно округлять вниз [в сторону минус бесконечности]. «Си» тоже требует соблюдать это равенство, и компиляторы, отбрасывающие дробную часть при i // j, должны заставить i % j принимать тот же знак, что и i.
Мало реальных случаев применения i % j, когда j отрицательно, но таких случаев много, когда j положительно, и практически во всех из них гораздо полезнее, чтобы i % j был >= 0. Если на часах сейчас 10, сколько на них было 200 часов назад? -190 % 12 == 2 — полезно; -190 % 12 == -10 — ошибка, которая ещё аукнется.
ОригиналWhy does -22 // 10 return -3?
It’s primarily driven by the desire that i % j have the same sign as j. If you want that, and also want:
i == (i // j) * j + (i % j)
then integer division has to return the floor. C also requires that identity to hold, and then compilers that truncate i // j need to make i % j have the same sign as i.
There are few real use cases for i % j when j is negative. When j is positive, there are many, and in virtually all of them it’s more useful for i % j to be >= 0. If the clock says 10 now, what did it say 200 hours ago? -190 % 12 == 2 is useful; -190 % 12 == -10 is a bug waiting to bite.
(Programming FAQ — Python 3.7.0 documentation)
zuborg
25.08.2018 20:00Если следовать этой логике, то -100 минут будет -2ч+20м, вместо -1ч40м.
Хотя стрелка будет указывать на 20м (если отсчитывать -100 минут от 0:00), да…
В общем, и так и так можно нарваться на неприятности, поэтому случаи с отрицательными числами при взятии остатка лучше обрабатывать отдельной логикой, а не полагаться на реализацию в компиляторе или cpu.

Blacky0892
25.08.2018 16:04php
echo "19 % 12 = " . 19 % 12 . "\n"; echo "19 % -12 = " . 19 % -12;
Выводит
19 % 12 = 7 19 % -12 = 7

samsergey
26.08.2018 05:41Haskell (GHC 8.0.1), как в Python
> 19 `divMod` 12 => (1,7) > 19 `divMod` (-12) => (-2,-5)


zuborg
Лучше рассказал бы, зачем вообще кому-то может понадобиться брать остаток от деления на отрицательное число. Ну, кроме как на собеседовании или позанудствовать, конечно…
kot_mapku3
Так в шифровании применяется. Я даже помню вопрос на стак выкладвал, потому что никак не мог посчитать уравнение, а там как раз такая арифметика была.
p.s. в итоге решил сам
zuborg
Ок, если не трудно, подскажите пожалуйста, в каком именно алгоритме шифрования используются отрицательные числа, по которым нужно брать остаток деления. Мне просто интересно, собственно, я таких не знаю и нагуглить сходу не получается.
kot_mapku3
Афинное шифрование, например. Т.е. у вас есть монограммы и каждая буква шифруется формулой: E(x)=(ax+b)%m. Тут-то и применяется. У меня даже было несколько живых примеров, надо поискать просто(т.к. в тетрадке)
zuborg
В афинном шифровании m — это кол-во букв в алфавите (биграмм, триграмм..). Оно не может быть отрицательным.
kot_mapku3
Но вы можете использовать сопоставление отрицательных чисел буквам и тогда получится отрицательный ответ.
zuborg
Тем не менее, в афинном шифровании (да и в остальных мне известных криптографических методах) взятие остатка от деления на отрицательное число не используется.
Генерация псевдо-случайных чисел оперирует либо битами, либо беззнаковыми числами. Операция деления и взятия остатка, в отличие от умножения, не дешевая, и на практике в генерации псевдо-случайных чисел не используется.
InterceptorTSK
В джаве полно беззнаковых чисел ага?
И более того, если где-то и есть возможность прилепить беззнаковые числа, то лучше разработать такой алгоритм, что бы все таки числа были со знаком, для совместимости оно будет проще потом в реализациях на разных языках.
И вообще кое-где беззнаковые — некомплиант…
И выходит так что да, алгоритмы лучше лепить сразу на знаковых числах. Тем более что оно вовсе не сложно как кажется на первый взгляд.
Я же например стараюсь вообще беззнаковые не использовать, ибо потом можно здорово геморроя хапнуть.
Deerenaros
Гхм. Что? Простите. Не так выразился.
ЧТО?!
На самом деле, unsigned в java не завезли, потому что не смогли. Почему не смогли? Скорее всего выбилось из дизайна виртуальной машины, а добавление поддержки «отдельной» арифметики было слишком сложно… Ну… И повелось, гхм. Вообще, беззнаковая арифметика не просто нужна, она кислородоподобна! Но на таких языках, как Java контроль памяти невозможен и обход ограничений через большую размерность не такая уж и проблема. А так, любая работа с криптографией, сетью, числодробительной графикой и прочей магией — убога, ужасна, стуло- и столо- (а в особых случаях, и мониторо-) ломающая.
Что до геморроя. Не знаю, может мне очевидно поведение unsigned. С другой стороны, может я чего-то действительно не понимаю, поэтому банально не вижу проблем. В остальном, сколько не работал с embedded на Си и Си++, пока только uint32_t, uint16_t и uint8_t. int32_t, int16_t и int8_t возникают в довольно редких, практически единичных случаях. Да и в принципе, отрицательные числа, внезапно, оказывается довольно редким явлением. И на самом деле обойтись без них — спокойно, хоть вручную проверяй знаковый бит. Куда запутаннее, сложнее и интереснее плавающие запятые, но это тема отдельной истории.
kot_mapku3
И не только этим шифрованием един. Это также может использоваться в различных реализациях генераторов псевдо-случайных чисел.
kot_mapku3
Ну собственно, вот статья: там же кроме положительных можно использовать отрицательные в связке с биграммами, триграммами и т.д.
Konachan700
Math.abs(Random.get() % 128) — сделает случайное число от нуля до 127. Крайне удобно.
UPD: а, блин, про отрицательное не заметил…
andreishe
Крайне удобно, но неправильно, если вам важно распределение.
IntActment
Однажды мне довелось столкнуться с этим — писал свой клон майнкрафта на Юнити, и мне нужно было получить значение координаты Х и У относительно «текущего» чанка (т.е. к примеру, глобальная округленная координата Х равна 35, чанки имеют размер 16 на 16, следовательно, первая мысль — взять остаток от деления 35 % 16 и получить искомое «3»), но как только мы подаем на вход отрицательную координату, получаем не то, что ожидали. К слову, подобная функция конвертации глобальных координат в локальные использовалась много где (каждый чанк хранит свои данные о ландшафте в виде массива [16, 16, 256]).