Человеческий мозг по своей природе очень плохо умеет оценивать вероятность срабатывания случайных событий, на основании выданной числовой оценки. И довольно хорошо на основании качественных оценок. А все потому, что человек мысленно делает конвертацию числовых вероятностей в качественные оценки, и делает это очень субъективно:
В статье будут рассмотрены следующие вопросы:
В процессе эволюции человеческий мозг учился очень хорошо оперировать качественными оценками событий и образами своего опыта. А числа и абстрактную числовую оценку вероятности «случайных» событий человек придумал сравнительно недавно [1]. Тем не менее эти числа человек в своих оценках всё равно преобразует в качественные представления: чуть-чуть, мало, много, опасно, безопасно, достаточно. Оценки эти всегда зависят от контекста и субъективного отношения к этому контексту. Именно это и является основной причиной ошибочных числовых допущений.
В качестве примера будет рассмотрена пошаговая игра Disciples 2 [2]. В данной части статьи не будет рассматриваться качество генерации случайных чисел конкретно в этой игре. Про их генерацию будет достаточно данных во второй части статьи.
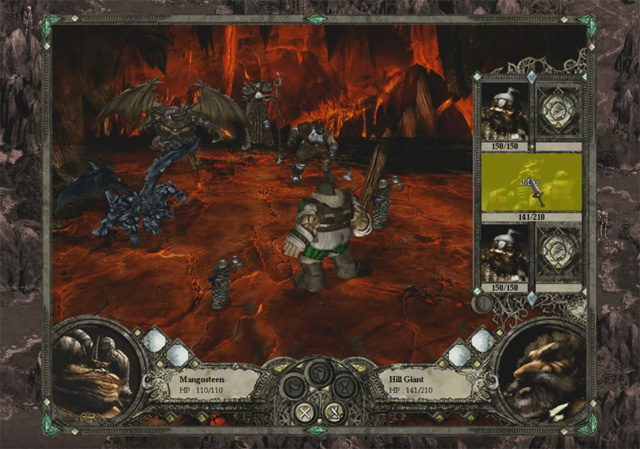 Disciples 2 — типичный промах [2]
Disciples 2 — типичный промах [2]
Стандартная атака ближнего боя имеет шанс попадания 80%. Обычно этот шанс воспринимается игроком как "почти всегда", а риск промаха — "изредка / время от времени". Вероятность промахнуться 2 раза подряд при двух атаках равна 4%. Игрок этот риск воспринимает как "почти никогда / такое будет случаться крайне редко". И когда подобное случается, игроки возмущаются на «кривой рандом»: [3]; [4].
Но в ситуациях с двумя промахами подряд и оценкой риска в 4% беглая оценка игроком имеет несколько ошибочных допущений:
1. 4% это вовсе не "почти никогда". Это событие, которое будет случаться в каждом 25-ом независимом эксперименте (в среднем).
2. Оценка проводится на неправильном отрезке времени. Минимальным отрезком замера атак по 80% следует брать не 2 атаки, а все атаки одного класса (~80%) за время «настороженной» памяти игрока. Чаще всего за это время можно взять долгую игровую сессию или вообще всю игру, тут всё зависит от типа игры, памяти игрока и предпочтений считающего.
Так как настоящей статистики использования этой игры у меня нет, я буду исходить из предположения, что долгая игровая сессия в Disciples 2 длится 3 часа и за это время совершается около 250 атак с меткостью ~80%. Стоит заметить, что промахи врагов следует игнорировать, т.к. их промахи игрока не злят, и он редко их запоминает.
Так вот, оценивать следует ситуацию: «За все 250 атак ни разу не произойдет 2 промахов подряд».
Для подсчета вероятности истинности данного события была использована рекуррентная формула: P1(n)=0.8*P1(n-1)+0.16*P1(n-2). В выведении этой формулы я воспользовался помощью сообщества, цитата вычислений, подробности и результат приведены ниже.
Для решения задачи вместо того, чтобы разбираться с методами решения рекуррентных соотношений, был написан маленький javascript код для консоли браузера и вычислен результат.
В итоге ответ: 0.0001666846271670716
Или 0.0167%
Этот ответ совпадает с ответом другого автора Kojiec9: 0.000166684627177505 [6], который использовал свой выработанный метод с пятиричной системой счисления и вычислил результат по своей формуле в Паскале. Незначительные различия в ответах, объясняются, судя по всему, округлениями float чисел.
Так вот, за 3 часа игры в Disciples 2 игрок имеет шанс избежать двойного промаха при 80% меткости всего в 0.0167%. Вот это уже действительно очень маловероятно. (а вероятность хотя бы одного двойного промаха, соответственно равна 99.9833%).
 Рост вероятности хотя бы одного двойного промаха с ростом числа экспериментов
Рост вероятности хотя бы одного двойного промаха с ростом числа экспериментов
Про несовершенство и искажения человеческой памяти, кстати, вообще целые исследования и книги существуют: «Иллюзии мозга. Когнитивные искажения из-за переизбытка информации» [7]; «Не верьте своему мозгу» [8], если вас эта тема заинтересовала, рекомендую начать ознакомление с этих статей.
3. Третье неверное допущение — это ожидание зависимости во взаимно независимых экспериментах.
То есть после первого промаха игрок думает:
«Так, персонаж промахнулся с меткостью 80%. Теперь-то он точно попадёт, ведь риск двойного промаха равен всего 4%».
А вот и нет. После первого промаха риск очередного промаха будет так же равен 20%. Ведь прошлая атака уже случилась и никак не влияет на будущий выстрел. Более того, если до первой атаки вероятность двойного промаха была равна 4%, то после первого промаха вероятность двойного промаха становится уже 20%, то есть относительно ожиданий игрока риск только возрастает.
Эта особенность человеческого мозга особенно привлекательна для манипуляций со стороны казино (и им подобных) в азартных играх (подробнее об устройстве игровых автоматов от производителя [9]).
Ещё интересные примеры заблуждений человеческого мозга можно почерпнуть в статьях про баланс Яна Шрайбера «Level 5: Probability and Randomness Gone Horribly Wrong» (Уровень 5. Вероятность и случайность пошли вразнос) [10].
Используемый в играх термин «Генератор случайных чисел» (RNG / random number generator) почти всегда в действительности означает «Генератор псевдослучайных чисел» [11]. Главной особенностью этого генератора является его воспроизводимость. Воспроизводимость означает то, что, зная изначальный порождающий элемент (или зерно / seed) всегда будет получена одна и та же последовательность случайных (псевдослучайных) чисел. В некоторых играх этот эффект проявляется в том, что после перезагрузки игры последовательность попаданий и промахов остается неизменной. А в других играх не остается той же самой.
А все дело в том, как применяется этот генератор псевдослучайных чисел и какие дизайнерские цели преследует разработчик.
Чтобы лучше понять принцип работы генератора псевдослучайных чисел, можно рассмотреть способ его реализации в первых классических играх, когда ресурсы компьютеров (и консолей) были особенно сильно ограниченны. (Углубленное описание примеров и их особенностей читайте в статье «How classic games make smart use of random number generation» [12].)
 How classic games make smart use of random number generation [12]
How classic games make smart use of random number generation [12]
В Final Fantasy I использовались несколько таблиц с заранее заданными фиксированными числами с 256 значениями в каждой таблице:
В качестве зерна (порождающего элемента) в Final Fantasy I используется порядковый номер (индекс) фиксированного значения в таблице. То есть, зная место, откуда будут дальше выбираться случайные числа, можно точно предсказать какое случайное число будет выдано после 1000 проверок. В более сложных алгоритмах генерации псевдослучайных чисел зерно используется не так просто, но основной принцип и эффект остаются.
Сейчас для генерации псевдослучайных чисел в основном используются стандартные библиотеки используемых языков программирования. В качестве источника энтропии чаще всего используется текущее системное время. Для нужд игровой индустрии характеристик стандартных библиотек обычно хватает. Недостатки генератора и источника энтропии используются игроками очень редко из-за сложности их вычисления и манипулирования. Обычно это остаётся уделом спидранеров-программистов (например, взламывающего логику Pokemon Colosseum [13]), а значит разработчикам такие тонкости чаще всего разумнее игнорировать.
1. Зерно фиксируется на момент старта миссии или игровой кампании.
Последствия для игрока: перезагрузка игры не изменит факт промаха персонажем (назовем его чокнутым Фиделем), даже если вероятность его попадания равна 99%. Однако, перед попыткой попасть игрок может совершить какое-либо другое действие, которое использует случайное число, например, походит другим персонажем — лысым Миком. В результате этого несчастливое случайное число будет использовано лысым Миком, а на чокнутого Фиделя будет использовано следующее случайное число в последовательности — тогда он, возможно, попадёт.
Как игрок может злоупотребить этим: если бросок с меткостью 50% приводит к промаху, то можно перезагрузиться и попробовать атаку с меткостью чуть-чуть повыше (55%), пока не попадёт. После попадания сохраниться и повторить это с другими бросками.
Положительные последствия для разработчика:
1) Игру можно воспроизвести пошагово, если хранить только начальное состояние, зерно и последовательность действий. Благодаря этому можно показывать повторы и даже очень компактно хранить файлы сохранений. Способ позволяет очень сильно сэкономить занимаемое место на диске/памяти.
2) Защита внутренних азартных игр, чтобы сохранение/загрузка не позволяла игроку обанкротить всех встречающихся NPC соперников.
Пример:
Игра roguelike Brogue [14] использует этот способ, начиная с генерации игрового мира и заканчивая просчетом всех действий игрока. В результате этого в файле сохранения хранится только стартовое зерно и последовательность игровых команд. Дополнительный бонус этого эффекта в том, что игру можно начать с выбранным номером зерна, предварительно выбрав наиболее интересный мир в таблицах сгенерированных миров Brogue [15].
 Brogue roguelike — официальный сайт [14]
Brogue roguelike — официальный сайт [14]
2. Зерно не фиксируется или обновляется каждый раз после перезагрузки.
Последствия для игрока: любая перезагрузка изменяет все расчеты в шансах попаданий.
Как игрок может злоупотребить этим: очень просто — несколько перезагрузок и самый маловероятный сценарий попадания может стать реальностью.
Положительные последствия для разработчика:
1) Игроки воспринимают такую игру как более честную с настоящей случайностью, просто из-за отсутствия знаний внутренних механик.
2) Игроки получают неофициальный лёгкий режим, который при желании позволяет сильно облегчить сложные участки.
3) Разработчик может прикрыть халяву разными методами: одним автосохранением на игру (то есть перезаписывание сохранений и перманентная смерть) или запретом сохранения во время миссии (в разных вариациях). А наиболее чувствительные участки (азартные мини игры) можно просчитывать на основании отдельного неизменного зерна, хотя технически это значительно труднее.
Пример:
Игра The Battle for Wesnoth [16] использует нефиксированное зерно с принципиально честной случайностью. Честность заключается в том, что иногда возможны совершенно маловероятные последовательности неудач, и движок игры их не корректирует. Результатом этого являются периодические гневные посты раздраженных игроков в адрес разработчиков игры.
 Reddit — супер ловкая русалка в Wesnoth [17]
Reddit — супер ловкая русалка в Wesnoth [17]
Также перед атакой игра предоставляет подробные расчеты вероятностей каждого из возможных исходов атаки: наносимый урон, получаемый урон и вероятность гибели одного из противников. Вывод этих вероятностей только накаляет гнев «неудачно походивших», т.к. уверившись в хороших шансах при атаке, сложно смириться с результатом, у которого была оценка 1 к 1000.
3. Зерно не фиксируется, а сами результаты подвергаются дополнительным манипуляциям.
Под манипуляциями я имею в виду такие динамические корректировки, в результате которых увеличивается ощущение правильной (справедливой) случайности за счёт потери настоящей псевдослучайности в получаемых числах.
Последствия для игрока: аналогично играм с нефиксированным зерном — перезагрузка позволяет пересчитать результаты.
Как игрок может злоупотребить этим: с помощью сейвскаминга можно подобрать выгодную комбинацию атак, но во многом зависит от способа реализации и наличия защитных механизмов со стороны разработчика.
Положительные последствия для разработчика: разработчик может контролировать редкость нежелательных исходов, делать видимость "честного рандома", увеличивать и уменьшать сложность игры. Если разработчик при подсчете шанса на попадания хранит и раздельно учитывает срабатывания для каждой команды, то он может сильно уменьшить злоупотребления от сейвскаминга, гарантируя, что свою среднеарифметическую порцию урона игрок всё равно получит.
Примеры:
Разработчик Carsten Germer использует функцию контролируемой случайности для редких и не только событий [18]. Например, чтобы гарантировать периодическое выпадение особо редкого бонуса с шансом 1 к 10000, он после каждого «промаха» увеличивает шансы по порядку: 1 к 9900; 1 к 9800; 1 к 9700… и так до фиксации события. А чтобы гарантировать отсутствие частых редкостей, он ввел дополнительную переменную, блокирующую срабатывание на 100% в течение 10 следующих проверок после прошлого срабатывания.
В своем рогалике Grue the Monster [19] я также использовал манипуляции со случайностями. Обычно при преследовании жертв персонаж игрока должен прятаться за их спинами, поджидая, когда они сделают шаг назад и попадут к нему в лапы. Обычно такой шанс равен 1/6 в открытом пространстве (1/2 в коридорах и 1/1 в тупиках), но чтобы уменьшить раздражающий эффект особенно невезучих ситуаций, перед каждой проверкой направления хода жертвы в 15% случаев она гарантированно шла в направлении к Гру.
Самый интересный случай: в игре Fire Emblem: The Binding Blade [20] была реализована скрытая механика определения попадания при атаках [21]. Традиционно для серии вероятность попадания показывается игрой в процентах от 0 до 100%. В более ранних играх серии факт попадания определялся одним случайным числом от 1 до 100: если выпадающее число (например, 61) меньше или равно вероятности попадания (например, 75), то засчитывается удар, если больше, то промах.
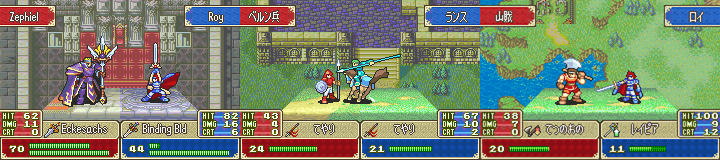 Fire Emblem: The Binding Blade [20]
Fire Emblem: The Binding Blade [20]
В данной части была введена щадящая система: вместо одного случайного числа бралось среднее двух случайных чисел, и это среднее сравнивалось со значением меткости. То есть случайное число в большей степени стремится к значению 50. Это приводит к искажению линейного эффекта случайности попадания: бойцы с меткостью больше 50% попадают чаще, чем в 50% случаев, а с меткостью меньше 50% значительно реже. А так как в игре подавляющее большинство персонажей игрока имеют большую меткость, а большинство врагов меньшую, то игрок получает очень серьёзное скрытое преимущество [21]. Ниже показан график этого эффекта, где синей линий показана частота попаданий в старой системе, а красной частота попаданий в новой в зависимости процента меткости атакующего. Например, при показываемой вероятности попадания в 90%, фактическая вероятность будет равна 98,1%, при 80% — 92,2%, а при 10% — всего 1,9%!
 Искажение шанса попадания. По оси Y фактическая вероятность, по оси X — показываемая игроку
Искажение шанса попадания. По оси Y фактическая вероятность, по оси X — показываемая игроку
Это, безусловно, не единственные примеры манипуляций со случайными числами и балансом, но найти их очень сложно. Поэтому помощь сообщества здесь будет особенно ценной.
Хочу отметить, что я не отношу к манипулируемой случайности процедурную генерацию, как таковую. Пример: рогалик сгенерировал случайный уровень со случайным набором врагов, ловушек, стен и тупиков. Если при этом был создан уровень, который невозможно пройти, то пример кривой разработки, недостаточно продуманного проектирования или слабого тестирования. Разработчик обязан процедурно проверять хотя бы базовые проблемы случайной генерации:
Такое вмешательство в случайные результаты не являются манипуляцией, а являются просто правилом минимально грамотного подхода к разработке. Используются эти проверки во всех способах генерации псевдослучайных чисел.
4. Вообще убрать элемент случайности из механики игры.
То есть результаты каждой атаки всегда имеют 100% вероятность попадания и фиксированный урон, а также постоянные правила срабатывания дополнительных эффектов. Вместо этого можно использовать случайные вычисления для косметических целей: периодические «позёвывания» ожидающих своего хода персонажей; отлетание чисел нанесенного урона; эффекты столкновений и взрывов. Тут нет никакой разницы, как генерировать случайные числа и насколько равномерно распределение.
Хотя и в этом случае можно использовать первые три способа в расчетах искусственного интеллекта, когда вражеские персонажи могут в какой-либо степени случайно выбирать цели для атаки или ходить командой в случайном порядке. Но это уже будет менее заметно для игрока и раздражающих ситуаций будет значительно меньше.
Последствия для игрока: перезагрузка либо никак не влияет на результаты, либо влияет незначительно.
Как игрок может злоупотребить этим: игрок может вычислить или найти в сети стабильную доминирующую стратегию и использовать только её. Стоит отметить, что для определённых групп игроков это является основным интересом в игре.
Положительные последствия для разработчика: разработчику значительно легче сбалансировать такую игру. Как минус — при этом возникающие доминирующие стратегии становятся стабильными, а значит, даже невезение игрока не сможет привести его к поражению, а приводит к исчезновению всяких неожиданностей, скуке и удалению игры. Игроки высокого класса почти всегда будут выигрывать у игроков классом пониже, для различных типов игр это может быть как преимуществом, так и недостатком.
Пример:
Любые шахматы с классическими правилами.
Также сюда подходят логические roguelike. Например, очень хорошо данный метод реализован в Desktop Dungeons Alpha [22].
 Desktop Dungeons Alpha [22]
Desktop Dungeons Alpha [22]
Здесь результаты последовательности атак всегда одинаковы и заранее просчитываемы. Однако за счет случайной (процедурной) генерации игровых подземелий и наличия тумана войны, игра приобретает свою уникальную реиграбельность лучших рогаликов.
Таким образом, в статье рассмотрены две подтемы случайности в играх:
- 80% попадания выстрела в игре — ну это почти гарантированное попадание;
- 80% того, что ваш товарищ хоть когда-нибудь отдаст долг — не-не-не, так не пойдёт, это слишком большой риск;
- 5% получения критического урона он NPC врага — маловероятно, риск можно игнорировать;
- 1% риск падения сосульки, если пройти под крышей с капающими метровыми сосульками — ещё чего, лучше обойти с другой стороны тротуара;
- 51% вероятность выигрыша в мини-игре в большой РПГ — можно рассчитывать на то, что после 20 ставок я чуть-чуть выиграю или, как минимум, останусь при своих… через 20 ставок… как такое могло случиться, что я проиграл половину всего своего золота? Тут явно сломан генератор случайных чисел!

В статье будут рассмотрены следующие вопросы:
- ошибочные допущения в оценке вероятностей;
- конкретные примеры заблуждений игроков и фактические вероятности «редких» событий;
- генератор случайных чисел (вообще-то псевдослучайных);
- ранние простые генераторы псевдослучайных чисел на примере Final Fantasy I;
- подходы к реализации случайных событий с воспроизводимостью и без;
- примеры удачно внедренных разных подходов и манипуляции в Fire Emblem.
I. Ошибочные допущения в оценке вероятностей
В процессе эволюции человеческий мозг учился очень хорошо оперировать качественными оценками событий и образами своего опыта. А числа и абстрактную числовую оценку вероятности «случайных» событий человек придумал сравнительно недавно [1]. Тем не менее эти числа человек в своих оценках всё равно преобразует в качественные представления: чуть-чуть, мало, много, опасно, безопасно, достаточно. Оценки эти всегда зависят от контекста и субъективного отношения к этому контексту. Именно это и является основной причиной ошибочных числовых допущений.
В качестве примера будет рассмотрена пошаговая игра Disciples 2 [2]. В данной части статьи не будет рассматриваться качество генерации случайных чисел конкретно в этой игре. Про их генерацию будет достаточно данных во второй части статьи.

Стандартная атака ближнего боя имеет шанс попадания 80%. Обычно этот шанс воспринимается игроком как "почти всегда", а риск промаха — "изредка / время от времени". Вероятность промахнуться 2 раза подряд при двух атаках равна 4%. Игрок этот риск воспринимает как "почти никогда / такое будет случаться крайне редко". И когда подобное случается, игроки возмущаются на «кривой рандом»: [3]; [4].
Но в ситуациях с двумя промахами подряд и оценкой риска в 4% беглая оценка игроком имеет несколько ошибочных допущений:
1. 4% это вовсе не "почти никогда". Это событие, которое будет случаться в каждом 25-ом независимом эксперименте (в среднем).
2. Оценка проводится на неправильном отрезке времени. Минимальным отрезком замера атак по 80% следует брать не 2 атаки, а все атаки одного класса (~80%) за время «настороженной» памяти игрока. Чаще всего за это время можно взять долгую игровую сессию или вообще всю игру, тут всё зависит от типа игры, памяти игрока и предпочтений считающего.
Так как настоящей статистики использования этой игры у меня нет, я буду исходить из предположения, что долгая игровая сессия в Disciples 2 длится 3 часа и за это время совершается около 250 атак с меткостью ~80%. Стоит заметить, что промахи врагов следует игнорировать, т.к. их промахи игрока не злят, и он редко их запоминает.
Так вот, оценивать следует ситуацию: «За все 250 атак ни разу не произойдет 2 промахов подряд».
Для подсчета вероятности истинности данного события была использована рекуррентная формула: P1(n)=0.8*P1(n-1)+0.16*P1(n-2). В выведении этой формулы я воспользовался помощью сообщества, цитата вычислений, подробности и результат приведены ниже.
Можно попробовать применить индукцию. Введём несколько обозначений. Вероятность сохранить лапу после n-й вылазки обозначим P(n). Представим эту вероятность в виде суммы двух вероятностейЦитата с решением задачи от пользователя Serbbit [6]
P(n) = P1(n)+P2(n), где P1(n) это вероятность, при которой крайняя n-ая вылазка оказалась удачной, а P2(n) — неудачной.
Может показаться что P1 и P2 пропорциональны 0.8 и 0.2, но это не так. Из-за того что мы рассматриваем не любые возможные исходы, а только те, которые сохранили лапу еноту.
Попробуем теперь вывести рекуррентную формулу
P1(n)=0.8*(P1(n-1)+P2(n-1))
P2(n)=0.2*P1(n-1)
Подставим P2 в формулу для P1 получим
P1(n)=0.8*P1(n-1)+0.16*P1(n-2)
Дальше Решение рекуррентных соотношений [5]
Для решения задачи вместо того, чтобы разбираться с методами решения рекуррентных соотношений, был написан маленький javascript код для консоли браузера и вычислен результат.
var P1 = [];
P1[0] = 1;
P1[1] = 1;
for (var n=2; n<=250; n++) {
P1[n] = 0.8 * P1[n-1] + 0.16 * P1[n-2];
console.log(n + ') ' + P1[n]);
}
// ответ: 250) 0.0001666846271670716
В итоге ответ: 0.0001666846271670716
Или 0.0167%
Этот ответ совпадает с ответом другого автора Kojiec9: 0.000166684627177505 [6], который использовал свой выработанный метод с пятиричной системой счисления и вычислил результат по своей формуле в Паскале. Незначительные различия в ответах, объясняются, судя по всему, округлениями float чисел.
Так вот, за 3 часа игры в Disciples 2 игрок имеет шанс избежать двойного промаха при 80% меткости всего в 0.0167%. Вот это уже действительно очень маловероятно. (а вероятность хотя бы одного двойного промаха, соответственно равна 99.9833%).

Про несовершенство и искажения человеческой памяти, кстати, вообще целые исследования и книги существуют: «Иллюзии мозга. Когнитивные искажения из-за переизбытка информации» [7]; «Не верьте своему мозгу» [8], если вас эта тема заинтересовала, рекомендую начать ознакомление с этих статей.
3. Третье неверное допущение — это ожидание зависимости во взаимно независимых экспериментах.
То есть после первого промаха игрок думает:
«Так, персонаж промахнулся с меткостью 80%. Теперь-то он точно попадёт, ведь риск двойного промаха равен всего 4%».
А вот и нет. После первого промаха риск очередного промаха будет так же равен 20%. Ведь прошлая атака уже случилась и никак не влияет на будущий выстрел. Более того, если до первой атаки вероятность двойного промаха была равна 4%, то после первого промаха вероятность двойного промаха становится уже 20%, то есть относительно ожиданий игрока риск только возрастает.
Эта особенность человеческого мозга особенно привлекательна для манипуляций со стороны казино (и им подобных) в азартных играх (подробнее об устройстве игровых автоматов от производителя [9]).
Ещё интересные примеры заблуждений человеческого мозга можно почерпнуть в статьях про баланс Яна Шрайбера «Level 5: Probability and Randomness Gone Horribly Wrong» (Уровень 5. Вероятность и случайность пошли вразнос) [10].
II. Генератор случайных чисел
Используемый в играх термин «Генератор случайных чисел» (RNG / random number generator) почти всегда в действительности означает «Генератор псевдослучайных чисел» [11]. Главной особенностью этого генератора является его воспроизводимость. Воспроизводимость означает то, что, зная изначальный порождающий элемент (или зерно / seed) всегда будет получена одна и та же последовательность случайных (псевдослучайных) чисел. В некоторых играх этот эффект проявляется в том, что после перезагрузки игры последовательность попаданий и промахов остается неизменной. А в других играх не остается той же самой.
А все дело в том, как применяется этот генератор псевдослучайных чисел и какие дизайнерские цели преследует разработчик.
Чтобы лучше понять принцип работы генератора псевдослучайных чисел, можно рассмотреть способ его реализации в первых классических играх, когда ресурсы компьютеров (и консолей) были особенно сильно ограниченны. (Углубленное описание примеров и их особенностей читайте в статье «How classic games make smart use of random number generation» [12].)

В Final Fantasy I использовались несколько таблиц с заранее заданными фиксированными числами с 256 значениями в каждой таблице:
- для вычисления случайных сражений с каждым шагом в игровой карте алгоритм перемещался по таблице, изменяя индекс на 1 за раз, таким образом постепенно прокручивая все возможные значения — от этого зависел как сам факт столкновения, так и возможная группа противников;
- для вычисления результатов сражения тоже использовалась подобная таблица из 256 фиксированных значений, но перемещение по ней происходило не только с каждым очередным использованием псевдослучайного числа, но и каждые 2 кадра. То есть каждые 2 кадра алгоритм вхолостую прокручивал таблицу с числами, тем самым уменьшая риск прогнозируемых одинаковых последовательностей. Источником энтропии тут была неопределенность, сколько времени игрок будет думать до выбора очередной команды.
В качестве зерна (порождающего элемента) в Final Fantasy I используется порядковый номер (индекс) фиксированного значения в таблице. То есть, зная место, откуда будут дальше выбираться случайные числа, можно точно предсказать какое случайное число будет выдано после 1000 проверок. В более сложных алгоритмах генерации псевдослучайных чисел зерно используется не так просто, но основной принцип и эффект остаются.
Сейчас для генерации псевдослучайных чисел в основном используются стандартные библиотеки используемых языков программирования. В качестве источника энтропии чаще всего используется текущее системное время. Для нужд игровой индустрии характеристик стандартных библиотек обычно хватает. Недостатки генератора и источника энтропии используются игроками очень редко из-за сложности их вычисления и манипулирования. Обычно это остаётся уделом спидранеров-программистов (например, взламывающего логику Pokemon Colosseum [13]), а значит разработчикам такие тонкости чаще всего разумнее игнорировать.
III. Разные подходы к использованию генератора
1. Зерно фиксируется на момент старта миссии или игровой кампании.
Последствия для игрока: перезагрузка игры не изменит факт промаха персонажем (назовем его чокнутым Фиделем), даже если вероятность его попадания равна 99%. Однако, перед попыткой попасть игрок может совершить какое-либо другое действие, которое использует случайное число, например, походит другим персонажем — лысым Миком. В результате этого несчастливое случайное число будет использовано лысым Миком, а на чокнутого Фиделя будет использовано следующее случайное число в последовательности — тогда он, возможно, попадёт.
Как игрок может злоупотребить этим: если бросок с меткостью 50% приводит к промаху, то можно перезагрузиться и попробовать атаку с меткостью чуть-чуть повыше (55%), пока не попадёт. После попадания сохраниться и повторить это с другими бросками.
Положительные последствия для разработчика:
1) Игру можно воспроизвести пошагово, если хранить только начальное состояние, зерно и последовательность действий. Благодаря этому можно показывать повторы и даже очень компактно хранить файлы сохранений. Способ позволяет очень сильно сэкономить занимаемое место на диске/памяти.
2) Защита внутренних азартных игр, чтобы сохранение/загрузка не позволяла игроку обанкротить всех встречающихся NPC соперников.
Пример:
Игра roguelike Brogue [14] использует этот способ, начиная с генерации игрового мира и заканчивая просчетом всех действий игрока. В результате этого в файле сохранения хранится только стартовое зерно и последовательность игровых команд. Дополнительный бонус этого эффекта в том, что игру можно начать с выбранным номером зерна, предварительно выбрав наиболее интересный мир в таблицах сгенерированных миров Brogue [15].

2. Зерно не фиксируется или обновляется каждый раз после перезагрузки.
Последствия для игрока: любая перезагрузка изменяет все расчеты в шансах попаданий.
Как игрок может злоупотребить этим: очень просто — несколько перезагрузок и самый маловероятный сценарий попадания может стать реальностью.
Положительные последствия для разработчика:
1) Игроки воспринимают такую игру как более честную с настоящей случайностью, просто из-за отсутствия знаний внутренних механик.
2) Игроки получают неофициальный лёгкий режим, который при желании позволяет сильно облегчить сложные участки.
3) Разработчик может прикрыть халяву разными методами: одним автосохранением на игру (то есть перезаписывание сохранений и перманентная смерть) или запретом сохранения во время миссии (в разных вариациях). А наиболее чувствительные участки (азартные мини игры) можно просчитывать на основании отдельного неизменного зерна, хотя технически это значительно труднее.
Пример:
Игра The Battle for Wesnoth [16] использует нефиксированное зерно с принципиально честной случайностью. Честность заключается в том, что иногда возможны совершенно маловероятные последовательности неудач, и движок игры их не корректирует. Результатом этого являются периодические гневные посты раздраженных игроков в адрес разработчиков игры.

Также перед атакой игра предоставляет подробные расчеты вероятностей каждого из возможных исходов атаки: наносимый урон, получаемый урон и вероятность гибели одного из противников. Вывод этих вероятностей только накаляет гнев «неудачно походивших», т.к. уверившись в хороших шансах при атаке, сложно смириться с результатом, у которого была оценка 1 к 1000.
3. Зерно не фиксируется, а сами результаты подвергаются дополнительным манипуляциям.
Под манипуляциями я имею в виду такие динамические корректировки, в результате которых увеличивается ощущение правильной (справедливой) случайности за счёт потери настоящей псевдослучайности в получаемых числах.
Последствия для игрока: аналогично играм с нефиксированным зерном — перезагрузка позволяет пересчитать результаты.
Как игрок может злоупотребить этим: с помощью сейвскаминга можно подобрать выгодную комбинацию атак, но во многом зависит от способа реализации и наличия защитных механизмов со стороны разработчика.
Положительные последствия для разработчика: разработчик может контролировать редкость нежелательных исходов, делать видимость "честного рандома", увеличивать и уменьшать сложность игры. Если разработчик при подсчете шанса на попадания хранит и раздельно учитывает срабатывания для каждой команды, то он может сильно уменьшить злоупотребления от сейвскаминга, гарантируя, что свою среднеарифметическую порцию урона игрок всё равно получит.
Примеры:
Разработчик Carsten Germer использует функцию контролируемой случайности для редких и не только событий [18]. Например, чтобы гарантировать периодическое выпадение особо редкого бонуса с шансом 1 к 10000, он после каждого «промаха» увеличивает шансы по порядку: 1 к 9900; 1 к 9800; 1 к 9700… и так до фиксации события. А чтобы гарантировать отсутствие частых редкостей, он ввел дополнительную переменную, блокирующую срабатывание на 100% в течение 10 следующих проверок после прошлого срабатывания.
В своем рогалике Grue the Monster [19] я также использовал манипуляции со случайностями. Обычно при преследовании жертв персонаж игрока должен прятаться за их спинами, поджидая, когда они сделают шаг назад и попадут к нему в лапы. Обычно такой шанс равен 1/6 в открытом пространстве (1/2 в коридорах и 1/1 в тупиках), но чтобы уменьшить раздражающий эффект особенно невезучих ситуаций, перед каждой проверкой направления хода жертвы в 15% случаев она гарантированно шла в направлении к Гру.
Самый интересный случай: в игре Fire Emblem: The Binding Blade [20] была реализована скрытая механика определения попадания при атаках [21]. Традиционно для серии вероятность попадания показывается игрой в процентах от 0 до 100%. В более ранних играх серии факт попадания определялся одним случайным числом от 1 до 100: если выпадающее число (например, 61) меньше или равно вероятности попадания (например, 75), то засчитывается удар, если больше, то промах.

В данной части была введена щадящая система: вместо одного случайного числа бралось среднее двух случайных чисел, и это среднее сравнивалось со значением меткости. То есть случайное число в большей степени стремится к значению 50. Это приводит к искажению линейного эффекта случайности попадания: бойцы с меткостью больше 50% попадают чаще, чем в 50% случаев, а с меткостью меньше 50% значительно реже. А так как в игре подавляющее большинство персонажей игрока имеют большую меткость, а большинство врагов меньшую, то игрок получает очень серьёзное скрытое преимущество [21]. Ниже показан график этого эффекта, где синей линий показана частота попаданий в старой системе, а красной частота попаданий в новой в зависимости процента меткости атакующего. Например, при показываемой вероятности попадания в 90%, фактическая вероятность будет равна 98,1%, при 80% — 92,2%, а при 10% — всего 1,9%!

Это, безусловно, не единственные примеры манипуляций со случайными числами и балансом, но найти их очень сложно. Поэтому помощь сообщества здесь будет особенно ценной.
Хочу отметить, что я не отношу к манипулируемой случайности процедурную генерацию, как таковую. Пример: рогалик сгенерировал случайный уровень со случайным набором врагов, ловушек, стен и тупиков. Если при этом был создан уровень, который невозможно пройти, то пример кривой разработки, недостаточно продуманного проектирования или слабого тестирования. Разработчик обязан процедурно проверять хотя бы базовые проблемы случайной генерации:
- проход к выходу всегда должен быть хотя бы в единственном числе. Тут помогают любые алгоритмы поиска пути;
- серия ловушек должна иметь возможность обхода, и если их создаётся слишком много в одном месте, то алгоритм должен вычислить их плотность и удалить лишние;
- слишком сильные враги должны предоставлять хотя бы один из доступных способов их «прохождения»: грубой силой; свитками и зельями; особыми артефактами или возможностью просто от них убежать.
Такое вмешательство в случайные результаты не являются манипуляцией, а являются просто правилом минимально грамотного подхода к разработке. Используются эти проверки во всех способах генерации псевдослучайных чисел.
4. Вообще убрать элемент случайности из механики игры.
То есть результаты каждой атаки всегда имеют 100% вероятность попадания и фиксированный урон, а также постоянные правила срабатывания дополнительных эффектов. Вместо этого можно использовать случайные вычисления для косметических целей: периодические «позёвывания» ожидающих своего хода персонажей; отлетание чисел нанесенного урона; эффекты столкновений и взрывов. Тут нет никакой разницы, как генерировать случайные числа и насколько равномерно распределение.
Хотя и в этом случае можно использовать первые три способа в расчетах искусственного интеллекта, когда вражеские персонажи могут в какой-либо степени случайно выбирать цели для атаки или ходить командой в случайном порядке. Но это уже будет менее заметно для игрока и раздражающих ситуаций будет значительно меньше.
Последствия для игрока: перезагрузка либо никак не влияет на результаты, либо влияет незначительно.
Как игрок может злоупотребить этим: игрок может вычислить или найти в сети стабильную доминирующую стратегию и использовать только её. Стоит отметить, что для определённых групп игроков это является основным интересом в игре.
Положительные последствия для разработчика: разработчику значительно легче сбалансировать такую игру. Как минус — при этом возникающие доминирующие стратегии становятся стабильными, а значит, даже невезение игрока не сможет привести его к поражению, а приводит к исчезновению всяких неожиданностей, скуке и удалению игры. Игроки высокого класса почти всегда будут выигрывать у игроков классом пониже, для различных типов игр это может быть как преимуществом, так и недостатком.
Пример:
Любые шахматы с классическими правилами.
Также сюда подходят логические roguelike. Например, очень хорошо данный метод реализован в Desktop Dungeons Alpha [22].

Здесь результаты последовательности атак всегда одинаковы и заранее просчитываемы. Однако за счет случайной (процедурной) генерации игровых подземелий и наличия тумана войны, игра приобретает свою уникальную реиграбельность лучших рогаликов.
Заключение
Таким образом, в статье рассмотрены две подтемы случайности в играх:
- Ошибочные допущения в оценке вероятностей. Описаны интуитивные допущения, которые делает игрок, и которые часто оказываются неправильными из-за их субъективности. Основной вывод: настоящая случайность не только не гарантирует того, что пользователи останутся довольны, но даже может привести к обратному эффекту.
- Генерация псевдослучайных чисел. Описаны разные подходы к использованию случайности. Удачные примеры реализации показывают, что независимо от выбранного подхода игра может получится интересной, неожиданной и с хорошей степенью реиграбельности.
Осознанное последовательное использование выбранного подхода позволяет разработчикам подчеркнуть их положительные стороны и минимизировать отрицательные.
Источники и литература
1. История математики, теория вероятностей — Википедия.
2. Disciples 2 — GOG Gold.
3. Disciples 2 — комментарий про кривой рандом №1.
4. Disciples 2 — комментарий про кривой рандом №2.
5. Решение рекуррентных соотношений.
6. Цитата с решением задачи от пользователя Serbbit.
7. Иллюзии мозга. Когнитивные искажения из-за переизбытка информации.
8. Не верьте своему мозгу.
9. Игровой аппарат изнутри и снаружи. Обзор от производителя.
10. Level 5: Probability and Randomness Gone Horribly Wrong.
11. Генератор псевдослучайных чисел — Википедия.
12. How classic games make smart use of random number generation.
13. Controlling luck in video games — Pokemon Colosseum and XD.
14. Brogue roguelike — официальный сайт.
15. The Brogue Seed Scummer.
16. The Battle for Wesnoth.
17. Супер ловкая русалка в Wesnoth.
18. «Not So Random Randomness» in Game Design and Programming.
19. Grue the Monster roguelike.
20. Fire Emblem: The Binding Blade.
21. Random Number Generator in Fire Emblem.
22. Desktop Dungeons Alpha roguelike.
2. Disciples 2 — GOG Gold.
3. Disciples 2 — комментарий про кривой рандом №1.
4. Disciples 2 — комментарий про кривой рандом №2.
5. Решение рекуррентных соотношений.
6. Цитата с решением задачи от пользователя Serbbit.
7. Иллюзии мозга. Когнитивные искажения из-за переизбытка информации.
8. Не верьте своему мозгу.
9. Игровой аппарат изнутри и снаружи. Обзор от производителя.
10. Level 5: Probability and Randomness Gone Horribly Wrong.
11. Генератор псевдослучайных чисел — Википедия.
12. How classic games make smart use of random number generation.
13. Controlling luck in video games — Pokemon Colosseum and XD.
14. Brogue roguelike — официальный сайт.
15. The Brogue Seed Scummer.
16. The Battle for Wesnoth.
17. Супер ловкая русалка в Wesnoth.
18. «Not So Random Randomness» in Game Design and Programming.
19. Grue the Monster roguelike.
20. Fire Emblem: The Binding Blade.
21. Random Number Generator in Fire Emblem.
22. Desktop Dungeons Alpha roguelike.


adictive_max
Тут ещё есть такая тонкость, как не только соответствие игровых событий цифрам, но и соответствие цифр здравому смыслу.
Когда в XCOM штурмовик (с использованием всех возможных перков) делает подряд 4 выстрела из дробовика в цель размером с автобус, стоящую на соседней клетке, и ни разу не попадает, то всем пофиг на то, что это вписывается в «вероятность попадания 70%».
qnok Автор
Сюда ещё можно добавить несоответствие визуальной анимации пролетария пули сквозь цель, но фиксацию промаха в логах.
vaim
Jules: This was Divine Intervention! You know what «divine intervention» is?
drafff
А еще в последнем XCOM вшито динамическое изменение сложности: при идеальном прохождении ваши бойцы начинают чаще промахиваться, а враги чаще попадать. Но если вы играете плохо (обратная ситуация), то игра начинает вам «подыгрывать».
JediPhilosopher
С меткостью кстати не все так просто. Меня игроки для моего рогалика долго просили добавить меткость и шанс промаха. Но когда я подумал на эту тему, я увидел всего две альтернативы, и обе мне не понравились:
1. Начальная меткость довольно низкая. Имеется широкое поле для прокачки персонажей и ее апгрейда (что хорошо), но получаем описанную вами ситуацию — когда в начале игры вроде бы тренированные спецназовцы не могут в упор попасть в крысу из пистолета. Что меня тоже адово бесило в играх где такое было сделано.
2. Начальная меткость высокая. Но тогда не получится ее прокачивать. Если в начале игры у персонажей меткость уже около 80-90%, то у нас остается очень мало процентов, которые можно добить скиллами или предметами. Неинтересно получается, характеристика есть, а качать ее нельзя (или почти бесполезно).
В итоге и непонятно, как лучше быть.
adictive_max
ИМХО, меткость должна работать более широко, чем просто попал-не попал. Должен быть ещё и случайный множитель урона. Плюс должна зависеть не только от расстояния и препятствий, но от типа оружия. Это будет обыгрывать и то, что не каждое попадание наносит существенный урон цели, и отражать особенности оружия.
Например:
снайперская винтовка — шанс промаха на оптимальной дистанции 20%, но зато большой урон и высокий шанс крита (или ваншота)
дробовик — на оптимальной дистанции шанс промаха 5%, но и в 70% урон пройдёт лишь частично, а шанс крита очень низок
огнемёт — 100% попадание, 100% урон, но без критов и можно зацепить себя, если цель слишком близко
что-то типа того.
И конечно оно должно напрямую зависеть от размера и скорости врагов. Попасть в крысу (реалистичного размера) из пистолета на самом деле довольно сложно, но вот в слона из дробовика шанс должен быть 100%.
qnok Автор
Я в некоторых новых играх видел, когда меткость влияла только на разброс урона. Так что тоже вариант.
dfgwer
(1-0.7)^4=0.0081
Если ты за прохождение делал такое 100 раз, то шанс увидеть такое хотя бы один раз 1-(1-((1-0.7)^4))^100)=0.55
В ХСОМ много испытаний и там гарантированно будут безумные совпадания.
Более того, если у ты обсуждаешь это на форуме где еще 10 человек, которые играли в ХСОМ, то это увеличивает силу невероятного еще в 10 раз. Шанс того что ты услышишь совершенно невероятную историю о том что штурмовик за два хода сделал 6 выстрелов с шансом 70% и все промахи, будет равно 51%.
mayorovp
Ни кто не спорит что при вероятности попадания в 70% это возможно. Вопрос в том какого фига вероятность попасть в рядом стоящий автобус из дробовика всего лишь 70%.
dfgwer
Автобус живой и не хочет быть застреленным, поэтому у него есть шанс отбить ствол оружия в сторону или уклониться или перекатиться за укрытие.
Можно еще поставить мод Long War (куча всего, в том числе разрешает 100% точность) и поставить галочку угловой размер, который увеличивает шанс попасть поблизости.
mayorovp
В таком случае я хочу видеть, как противник отбивает ствол оружия в сторону, уклоняется или перекатывается за укрытие. Видеть как спецназовец мажет в упор по неподвижному противнику я не хочу.
qnok Автор
Как это не прискорбно, но разработчики основные силы бросили на визуальную часть, а не на физику и мелкие детали. И выиграли от этого, что уже хорошо, так как такая реализация лучше похороненной франшизы.
voidMan
в Fallout 4 есть подобное, недавно наткнулся
Lexxnech
Про определяемый действиями игрока исход, вспомнилось, как наткнулся на дыру в одном из генераторов Diablo 2. База выпадающих из стоек с оружием/броней предметов определялась действиями игрока после входа на карту, и можно было без проблем подобрать маршрут, который обеспечивал нужный вид вещи в подавляющем большинстве случаев. Правда там явно работало несколько генераторов, так что повлиять на то, будет вещь обычной, магической и т.д. было нельзя.
Но для реалтаймовой и динамичной игры с достаточно глубокой механикой, даже удивительно, что возможность элементарной эксплуатации ГСЧ можно было наткнуться в процессе обычной игры, а не при углубленном ковырянии в механике.
KsiOwn1t
Не знаю почему, но в голове сразу всплыла Lineage 2 со своим «генератором случайностей»
от параметра accuracy зависела вся физ.атака у героев, от значений в одну-две-три единицы была огромная зависимость в попаданиях. Там сдвиг исчислялся для игрока в единицах по факту в % и больших, или же это мои — Ошибочные допущения в оценке вероятностей? =)
mrigi
С вероятностью попадания никаких ошибочных допущений нет. Мозг понимает, что этот мир не идеален и что постоянно идёт поток позитивных моментов и негативных. Четыре позитива (попадания) и один негатив (промах) — вполне уместная последовательность, чтобы держать мозг удовлетворенным. Даже переодические проскакивания двух негативов подряд не могут переломить баланс сами по себе. Но это только одна сторона, вторая — а достаточно ли 4 попадания из пяти, чтобы умерщвлять противников быстрее чем они появляются или убивают тебя? Если достаточно, то промахи и проценты вообще ни на что не влияют. Игрок и так во время игры двигается, выбегает из огня и всё такое. Промахнувшись можно ещё раз ударить и достигнуть результата, важно чтобы промахи не раздражали в процессе и всё. Математика тут вторична.
DjSebas
Этой статье явно не хватает комментариев Wargaming по поводу теории заговора. Надеюсь что хотя бы лет через 10-20 когда/если игра закроется они поделятся информацией о своих манипуляциях с генератором случайных чисел.
DrunkBear
В Sacred были случайные награды за сдачу квестов — вещь от мусорного до легендарного качества. Наткнулся случайно, когда кот сел на клавишу быстрой загрузки и я за квест получил совсем другую вещь, не ту, что минуту назад.
После этого прохождение игры стало очень простым.
Sirion
Ага) Боевой маг, ледяные осколки и призрачный луг. У других персонажей нет смысла слишком высоко вкачивать навык, потому что катастрофически растёт кулдаун. А у боевого мага призрачный луг кулдаун уменьшает.
LEXA_JA
Если я правилно помню, там была система, которая повышала шанс выпадения хороших предметов со временем, и сбрасывала добавочную вероятность после получения. Помню еще, что на старте игры, если не учить руны по первому времени, то они начинали чаще падать.
Sirion
Вероятность выпадения рун зависела от количества уже имеющихся рун. Поэтому ради максимального задротства имело смысл сначала просто побегать, а потом сдавать квесты.
mayorovp
Проще нового персонажа создать, а потом передать руны через сетевую игру. Еще их дублировать можно, но это уже читерство.
Sirion
Когда я играл в сейкред, о сетевой игре я мог лишь только мечтать)
mayorovp
Так напарник-то и не нужен, можно одному играть. Там весь фокус в том, что при сетевом прохождении кампании можно независимо загружать и сохранять мир и героев.
Просто выкидываем первым героем все руны на землю, сохраняемся, заходим в это сохранение вторым героем и подбираем их. Можно загружать сохранение несколько раз…
Sirion
Где ж ты был 15 лет назад?
JediPhilosopher
Помимо использования честного генератора (пусть и с подстройкой), можно вообще
сгенерировать последовательности результатов случайных действий, заранее их «причесать» (то есть пройтись по ним, вычистить из них всякие бесячие вещи типа двух промахов подряд) и зашить в игру просто в виде массива констант. Это такой промежуточный вариант между 3 и 4.
Вспоминается еще пример из какой-то HOMM, где у призраков был большой шанс уклониться от атаки, что делало их убийство довольно нетривиальным. Но в механике игры было зашито что трех уклонений подряд быть не может, если призраки уклонились два раза то третий удар 100% пройдет. Игроки быстро начали это абьюзить — брали много мелких стеков слабых юнитов, били призраков пока не получали два промаха подряд, затем били их основным мощным стеком со 100% шансом уничтожения.
suharik
Здравствуй, старый добрый Jagged Alliance II.
И тебе привет, Fallout II.
Velet
Стоило бы воспользоваться простейшими знаниями теории вероятности, есть формула Бернулли
AndreDeBonk
Не нравится, когда в играх корректируют «случайности» по принципу если шанс выпадения предмета 10%, значит на сотку случаев будет десять выпадений.
Теряется весь смысл этой случайности, исчезает бесконечность возможных вариантов развития событий (пять предметов подряд, или ноль на длительной серии).
Но для казуалов это заходит, такой «рандом» они считают правильным.
amakhrov
Вариант подобного "подкорректированного" случайного исхода есть в игре Годвилль.
Во время дуэли влияния игроков (атаки или лечилки) сгруппированы в блоки. Внутри блока гарантируется осечка ровно одного влияния.
Допустим, блок из 6 влияний — 5 из них гарантированно сработает, одно даст осечку (это может быть как самое первое, так и самое последнее — случайным образом, но всегда строго одно).
Это делает игровую механику более интересной, так как исход можно отчасти просчитать (и использовать против соперника) — по сравнению с честным рандомом.
dfgwer
Есть еще один вариант.
if( меткость > состояниезащиты) {состояниезащиты += уклонение; нанестидамаг;}
else {состояниезащиты -=меткость; показатьуклонение;}
Тут вообще нет рандома, очень просто, и дает равномерные легко просчитываемые шансы. В некоторых играх встречал. Обозвать могут «шансом» или честно указать как фичу.
qnok Автор
Это такой запас уклонения (или выносливости).
Сам задумываюсь уже довольно давно воспользоваться таким.
Можете вспомнить пару игр с такой механикой? Вы бы мне очень помогли, это будет отличным дополнением к следующей статье.
dfgwer
Это есть в Path of Exile, механика evasion, правда там еще много чего намешано.
И еще вроде в Диабло 2 было, механика брони. Других игр не могу вспомнить.
В ПоЕ начальное состояниезащиты равно уклонению, и если у врага точность меньше твоего уклонения ты получаеш гарантированное уклонение, иначе гарантированный хит. Если уклонение у тебя больше в N раз, то N первых ударов в уклонение уходит, а потом получаешь урон. Если уклонение у тебя меньше в N раз, N первых ударов наносит урон, а потом уклонение. Счетчик состояниезащиты сбрасывается через 4 секунды без получаемый ударов.
В долгой битве (точностьврага/(точностьврага+уклонение))=%полученныхударов
Довольно интересная механика, позволяющая стратегии вроде наскочил-ударил-отскочил. Правда в ПвП неочень, дает очень сильный бонус быстрым и вертлявым, они становятся неуязвимыми.
Можно поиграться с начальным значением состояниезащиты,
если 0 то первый удар всегда проходит
если равно уклонению, то по выше описанному сценарию
если равно Х, то при меткости выше Х, то первый удар всегда проходит, иначе всегда промах.
qnok Автор
Весьма оригинальный способ ухода от проблем случайной меткости.
losse_narmo
Так реализована удача/мораль в онлайн игре «Герои войны и денег».
В итоге, например, прокачав удачу, будешь ее получать строго через раз (и это описано в правилах как фича)
BorlandDelphi
Если сосулька упадёт, то сделать load saved game не получится. :(