
Мы добавили правила на основе квантовой теории в шашки, чтобы сделать их менее предсказуемыми и сломать стандартные тактики игры. Это не просто игра, это интерактивное представление квантовой теории с такими эффектами как суперпозиция и квантовая запутанность.
Квантовые шашки — плод
В наших квантовых шашках каждая шашка ведет себя как квантовый объект, что на практике означает следующее:
- Игрок не знает, есть ли на самом деле шашка в данной клетке поля, он видит лишь вероятность ее нахождения в указанной клетке.
- Шашки одного цвета ничем не отличаются друг от друга и вы, по сути, не оперируете отдельными шашками.
Смысл же и основные правила игры остаются как в классических шашках — два игрока, 8х8, нужно съесть все шашки противника.
Хотите попробовать? Установите бесплатные Quantum Checkers из App Store по ссылке.
Квантовые правила

Как я писал выше, то что вы видите на доске на самом деле не шашки, а их вероятности нахождения в данной клетке. В начале игры вероятность нахождения каждой шашки в ее классической стартовой позиции равна 1 или 100%. Чтобы сделать ход нужно выбрать шашку с которой вы хотите пойти, однако, в отличие от классических шашек, вы не выбираете куда ходить. Шашка с выбранной вами клетки ходит во все возможные согласно классическим правилам клетки и вероятность ее нахождения в них изменятся.
Например, если вы играете зелеными (да, в квантовых шашках мы решили использовать цвета повеселее) и пойдете шашкой из клетки E3, то состояние доски станет вот таким.
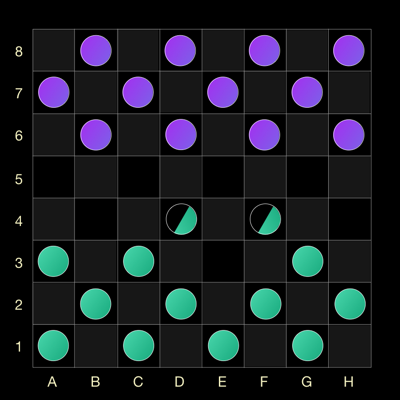
Половинка шашки означает, что вероятность ее нахождения в данной клетке равна 50%. Почему? Потому что выбранная шашка могла пойти в любую из этих клеток, а значит вероятность ее нахождения в каждой из них равна 50%. Полученный результат наглядно отражает принцип неопределенности в квантовой теории.
Сразу отмечу, что согласно принципу суперпозиции в одной клетке могут находится и шашки разных цветов! В этом случае заполненность шашки определенным цветом будет означать вероятность нахождения шашки этого цвета в данной клетке.Затем ваш соперник ходит своей фиолетовой шашкой, например, шашкой из клетки D6 и получает вот такой симметричный результат.
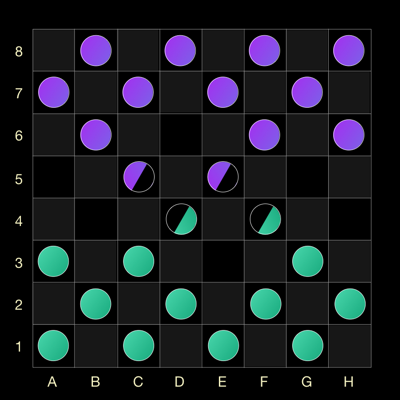
Нужно брать, подумаете вы. Да, нужно брать шашку противника согласно классическим правилам. И здесь начинается самая магия. Попробуем пойти зеленой шашкой из клетки F4. В момент, когда вы тапаете на клетку, игра вычисляет, есть ли шашка в данной клетке. Если вероятность равна 1, то все просто — шашка есть, если нулю, то тоже просто — шашки нет. Если же истина где-то посередине, то игра подкидывает кубик и таким образом определяет наличие шашки на поле.
Итак, тапаем. Есть два варианта развития событий:
- Шашки в выбранной клетке нет. В этом случае вам будет предложено пойти другой шашкой своего цвета. Да, в квантовых шашках, в ситуации, когда в выбранной вами клетке на самом деле не оказалось шашки (то есть она там может быть и была, но вы «измерили» эту клетку, и оказалось, что её там нет).
- Шашка в выбранной клетке есть. В этом случае она должна съесть фиолетовую шашку и доска будет выглядеть вот так:
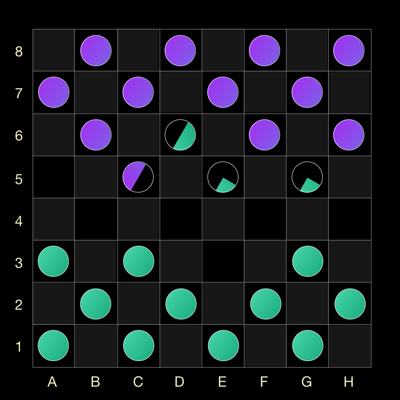
Почему картинка выглядит именно так? У нас было два варианта развития событий:
- Фиолетовая шашка была в клетке E5 и вероятность этого была 50%. Тогда опять же с вероятностью 50% зеленая шашка окажется в клетке D6.
- Фиолетовой шашки не было в клетке E5 и вероятность этого тоже 50%. Тогда зеленая шашка с вероятностью 25% окажется в клетке E5 и с 25% вероятностью в клетке G5.
При этом 50% вероятность нахождения шашки в клетке C5 сохраняется. На доске же под вашим именем отображается совокупная вероятность нахождения всех ваших шашек на поле. В начале она равна 12, так как у вас всего 12 шашек. После последнего хода вероятность скорее всего изменилась и согласно картинке выше совокупная вероятность для фиолетовых шашек будет равна 11,5. Ведь фиолетовых шашек стало на половинку меньше;)
Конец игры
Как победить при такой неопределенности? В классических шашках вы выигрываете, когда все шашки противника съедены или заблокированы.
В квантовых шашках обе ситуации могут произойти с некоторой вероятностью и игра заканчивается в одном из двух случаев:
- Совокупная вероятность нахождения шашек противника на поле стала меньше 1.
- Все оставшиеся шашки противника заблокированы с вероятностью больше 1.
В обоих случаях вы выигрываете с какой-то вероятностью, а не 100%. Возможна также 100% классическая победа.
Таким образом стратегия игры заключается в том, чтобы продумать наперед, с какой вероятностью ваша шашка окажется в том или ином поле и как это повлияет на дальнейшую игру. В отличии от классических шашек вариантов развития событий становится кардинально больше, а просчитать игру наперед становится очень сложно.
Не забудьте скачать игру в App Store и, конечно же, нам очень интересен ваш фидбек!
Комментарии (30)

berezuev
19.12.2018 10:20Попробуем пойти зеленой шашкой из клетки F4.
Вроде как в классических правилах можно есть еще и назад. Тогда вероятность съесть шашку равна 100%, т.к. мы одним ходом едим E5 и C5, не?)
bbelky Автор
19.12.2018 10:33Да, так ходят в «русских» шашках. У меня пример построен на правилах draughts — «английских» шашек. О чем мне стоило бы, конечно, упомянуть;) Спасибо, поправлю! В самой игре у нас поддерживаются оба варианта правил — можно выбрать.

vesper-bot
19.12.2018 11:41На C5 же та же шашка, что и на Е5, т.е. если мы съели на Е5, на С5 шашки нет и есть дальше нечего. Я в начале тоже думал, почему это на B4 нет шашки после хода F4 — нет, всё правильно. Нужно просто рассматривать доску как суперпозицию всех досок, в которых сделан ход шашкой на F4 во все стороны, механизм такой же, как в квантовых шахматах.

vesper-bot
19.12.2018 11:41Интересно, ходов через 20 (полуходов, в смысле) не слишком ли много окажется досок?

pxemul
19.12.2018 11:49Бывает такое. В русских правилах, когда появляются дамки и «размазываются» на полдоски, я видел несколько сотен досок. В английских больше двух десятков трудно получить. И потом доски не только плодятся, каждый ход приводит к измерению клетки и отбрасыванию части досок, так что их количество со временем изменяется немонотонно.

zuborg
19.12.2018 16:18Шашки в выбранной клетке нет
Если зеленой шашки не обнаружилось в F4, то вероятность её обнаружения в D4 должна составить 100% (по правилам квантовой механики, конечно)
При этом 50% вероятность нахождения шашки в клетке C5 сохраняется
Опять же, если фиолетовая шашка на E5 была бита, то вероятность её обнаружения в C5 теперь 0%. Или же, если фиолетовая шашка будет обнаружена на С5, то на E5 её нет и битой там она не может быть.
Кванты, они не только про вероятности, но и про корреляцию событий.
bbelky Автор
19.12.2018 16:41Если зеленой шашки не обнаружилось в F4, то вероятность её обнаружения в D4 должна составить 100%
Да, все верно.
Опять же, если фиолетовая шашка на E5 была бита, то вероятность её обнаружения в C5 теперь 0%
И тут верно, но в данном случае мы имеем дело с квантовой запутанностью. Пока мы при следующем ходе не проверим состояние фиолетовой шашки С5, которая в данном случае является шашкой Шредингера, мы не знаем состояние зеленых шашек в E5, G5 и D6. Как только мы это состояние проверим — мы получим реальную картину распределения вероятностей шашек.
Newbilius
20.12.2018 08:45Может попробовать добавить альтернативу, когда предлагается не просто выбрать другую, а перевести выбранную шашку в вероятность 0%, а у остальных связанных с ней — повысить вероятность?

pxemul
20.12.2018 11:38Так и происходит. Когда вы тыкаете в клетку, где есть шашка с не единичной вероятностью, бросается монетка и смотрится — там шашка, или нет. По результатам этого измерения все связанные (предыдущими ходами) с ней клетки тоже обновляются соответствующим образом. Например, если шашка там есть, это значит, что её нет в других местах, где она могла бы быть. Более того, если в «тех других» местах она могла оказаться съев что-то у соперника, то если её там на самом деле нет, то сопернку вернут съеденное.

pxemul
20.12.2018 11:31Не «получим реальную картину распределения вероятностей», а всего лишь проверим есть ли в выбранной нами клетке шашка или нет.

gban
20.12.2018 04:00Как все просто, главное — понять: шашка не существует...

Cerberuser
20.12.2018 04:40- Do not try and move the piece. That's impossible. Instead only try to realize the truth.
- What truth?
- There is no piece.
- There is no piece?
- Then you'll see that it is not the piece that moves, it is only yourself.
(Шашматрица)

gban
20.12.2018 07:37+1Итак, тапаем. Есть два варианта развития событий:
Шашки в выбранной клетке нет. В этом случае вам будет предложено пойти другой шашкой своего цвета.Это уже сапер какой-то… и половинчатое решение… а если в этот момент раздваивать поле?

bbelky Автор
20.12.2018 11:17Да, есть элемент сапера))) Полей (досок) итак почти всегда несколько — вверху доски показывается параметр boards. Если не подкидывать кубик и не проверять вероятность, то вам придется играть одновременно на нескольких досках. Думаю, что можно добавить визуализацию, чтобы показать все состояния досок.

WinPooh73
20.12.2018 10:03https://senseis.xmp.net/?QuantumGo
Интересная особенность квантового Го — при большом количестве частиц, как и в физическом мире, поведение системы стремится к классическому.

SERG-666
20.12.2018 10:55Все оставшиеся шашки противника заблокированы с вероятностью больше 1.
Какая-то необычная вероятность?.. Нет ли здесь опечатки?
pxemul
20.12.2018 11:41Есть, Вовчик не дружит с вероятностями. Там всё просто, как только есть вероятность проигрыша одного игрока, то он проигрывает и всё. Теоретически, наверное, возможна даже ситуация, когда проиграли оба.

SERG-666
20.12.2018 11:06Что такое «Совокупная вероятность»? Я в классической теории вероятностей не встречал такого понятия. Если, это сумма вероятностей, тогда это и пишите, или приведите определение этого понятия. Насколько я понимаю, вероятность события не бывает больше 1.

bbelky Автор
20.12.2018 11:30Да, что-то я не очень описал этот термин( Совокупная вероятность в моей статье — это сумма вероятностей всех шашек одного цвета находящихся на доске. Например, у вас осталось 8 шашек с вероятностью 1 и 2 шашки с вероятностью 0,5. Значит совокупная вероятность будет равна 9.


Sirion
Оригинально, но не до конца.
bbelky Автор
Да, квантовые шахматы это известная тема и видел даже какую-то реализацию в апсторе (в посте по ссылке игра уже не доступна). А у нас в планах заквантовать еще парочку игр, может и шахматы тоже — ничего сложного с технической точки зрения.
Sirion
Кстати, вы в гугл плей не планируете выкладывать сабж? Я бы с интересом попробовал, но мешают аппаратные ограничения.
bbelky Автор
Хотели бы, но опыта с андроид особо нет( нужен кто-то, кто готов был бы переписать фронт под андроид.
synedra
А в браузер?
bbelky Автор
Планируем сделать для андроид. Пойдет?
UncleAndy
В google play есть Quantum Chess. Квантовые шахматы, но суть похожа.
Sirion
Да я вот именно шашки больше люблю. Когда-то почти дотянул до кмс.