Используя протокол доказательства с нулевым разглашением из семейства SNARK, вы никогда не знаете правил игры. Эти правила устанавливают участники процедуры генерации доверенных параметров системы, однако после её завершения проверить эти правила не представляется возможным. Вы можете поверить в корректность генерации, но, если вы в ней не участвовали, стопроцентных гарантий у вас нет.

В последнее время в блокчейн сообществе всё чаще упоминаются различные zero knowledge протоколы (чтобы получить о них общее представление, рекомендую эту статью): в первую очередь в контексте приватности, реже в контексте масштабируемости и других.
Одним из наиболее изученных, а что важнее — реализованных является семейство протоколов zk-SNARK (Zero-Knowledge Succinct Non-Interactive Argument of Knowledge). Такой протокол используется, в частности, в криптовалюте Zcash. Популярность SNARK оправдана: протокол позволяет нам доказывать факты с нулевым разглашением, доказательства относительно невелики, и всё это с гарантиями безопасности, которые даёт нам современная криптография на эллиптических кривых.
Однако без минусов, как обычно, не обошлось: основным недостатком этого семейства zk-протоколов является необходимость в генерации начальных (доверенных) параметров системы — этот процесс также называют церемонией. Ведь для генерации используются подлежащие уничтожению секретные параметры — их называют токсичными. Главная проблема заключается в том, что в случае сохранения токсичных параметров, владеющий ими сможет доказывать ложные факты (в случае с Zcash — генерировать криптовалюту из воздуха).
Но немногие вспоминают о второй, не менее важной проблеме, которая также появляется из-за необходимости в генерации начальных параметров, но имеет другую природу и последствия — это проблема “маскировки” начальной задачи. Цель этой статьи — пролить немного света на эту несправедливо незамечаемую проблему SNARK протоколов.
Далее будет лишь поверхностно затронута математика, лежащая в основе SNARK протоколов. Если вам интересно в ней разобраться — советую цикл статей от Виталика Бутерина на эту тему.
Давайте рассмотрим процесс генерации доверенных параметров. Итак, у нас есть постановка задачи, факт решения которой мы хотим доказывать с нулевым разглашением. Например, мы хотим проверять знание корня квадратного уравнения:
По протоколу мы должны привести это уравнение к QAP (Quadratic Arithmetic Programs) виду. Далее для генерации и проверки доказательств необходимо получить начальные параметры. Оставим за скобками то, как из QAP получаются доверенные параметры, что это за параметры и как именно с их помощью можно проверять доказательства, чтобы не углубляться в тяжёлую математику. Отметим лишь, что параметры представлены в виде точек на эллиптической кривой:

Получены они из постановки задачи в виде QAP при помощи необратимой операции умножения на эллиптической кривой с использованием токсичных параметров.
Теперь, когда начальные параметры созданы, мы можем начать работу с доказательствами. В нашем случае можно сгенерировать и проверить доказательство того, что известен корень уравнения (например, ). При этом доказательство не будет раскрывать значение секрета (корня уравнения) и будет состоять из нескольких точек эллиптической кривой.
Однако, в силу математики, лежащей в основе протокола, если токсичные параметры сохранились у кого-то после церемонии, этот человек сможет доказывать ложные факты. Возвращаясь к нашему примеру, можно доказать, что 2 является корнем уравнения, хотя это, очевидно, не так.
Вторая опасность заключается в том, что можно намеренно оставить лазейку (backdoor) в постановке задачи. А именно, можно получить начальные параметры из уравнения:
В таком случае все честные участники будут играть по правилам: решать уравнение , а злоумышленник будет использовать лазейку — корень многочлена , и никто даже не догадается об этом. Ведь после церемонии система оперирует лишь публичными (доверенными) параметрами, которые получены при помощи необратимой операции умножения на эллиптической кривой. И следовательно, без публикации токсичных параметров (что абсурдно) невозможно проверить подлинность задачи, для который формируются доказательства.
Такого рода backdoor открывает участникам церемонии безграничные возможности для манипуляции системами, использующими zk-SNARK протоколы. Рассмотрим для примера систему, которая оперирует аккаунтами пользователей с различными правами (в криптовалютах аккаунт — это публичный ключ, а управлять средствами на нём может лишь обладатель соответствующего приватного ключа). Пусть система приватная, и факт владения аккаунтом (обладание приватным ключом в случае криптовалюты) доказывается с помощью zk-SNARK протокола. Тогда задача должна быть сформулирована так: “Доступ к аккаунту Y может получить тот, кто предоставит соответствующий приватный ключ X”.
Однако, если в ходе генерации доверенных параметров она будет сформулирована так: "Доступ к аккаунту Y может получить тот, кто предоставит соответствующий приватный ключ X или число 13", то участники церемонии, знающие секретное число 13, смогут получить доступ к аккаунту любого пользователя (доступ к средствам, если это криптовалюта).
В заключение стоит отметить, что критичность церемонии и вытекающих из неё угроз следует рассматривать отдельно для каждой конкретной системы. И в то же время, для всех систем, использующих SNARK протоколы, необходима надежная процедура генерации начальных параметров с гарантиями подлинности решаемой задачи и уничтожения токсичных параметров.

Две проблемы zk-SNARK
В последнее время в блокчейн сообществе всё чаще упоминаются различные zero knowledge протоколы (чтобы получить о них общее представление, рекомендую эту статью): в первую очередь в контексте приватности, реже в контексте масштабируемости и других.
Одним из наиболее изученных, а что важнее — реализованных является семейство протоколов zk-SNARK (Zero-Knowledge Succinct Non-Interactive Argument of Knowledge). Такой протокол используется, в частности, в криптовалюте Zcash. Популярность SNARK оправдана: протокол позволяет нам доказывать факты с нулевым разглашением, доказательства относительно невелики, и всё это с гарантиями безопасности, которые даёт нам современная криптография на эллиптических кривых.
Однако без минусов, как обычно, не обошлось: основным недостатком этого семейства zk-протоколов является необходимость в генерации начальных (доверенных) параметров системы — этот процесс также называют церемонией. Ведь для генерации используются подлежащие уничтожению секретные параметры — их называют токсичными. Главная проблема заключается в том, что в случае сохранения токсичных параметров, владеющий ими сможет доказывать ложные факты (в случае с Zcash — генерировать криптовалюту из воздуха).
Но немногие вспоминают о второй, не менее важной проблеме, которая также появляется из-за необходимости в генерации начальных параметров, но имеет другую природу и последствия — это проблема “маскировки” начальной задачи. Цель этой статьи — пролить немного света на эту несправедливо незамечаемую проблему SNARK протоколов.
Генерация начальных параметров
Далее будет лишь поверхностно затронута математика, лежащая в основе SNARK протоколов. Если вам интересно в ней разобраться — советую цикл статей от Виталика Бутерина на эту тему.
Давайте рассмотрим процесс генерации доверенных параметров. Итак, у нас есть постановка задачи, факт решения которой мы хотим доказывать с нулевым разглашением. Например, мы хотим проверять знание корня квадратного уравнения:
По протоколу мы должны привести это уравнение к QAP (Quadratic Arithmetic Programs) виду. Далее для генерации и проверки доказательств необходимо получить начальные параметры. Оставим за скобками то, как из QAP получаются доверенные параметры, что это за параметры и как именно с их помощью можно проверять доказательства, чтобы не углубляться в тяжёлую математику. Отметим лишь, что параметры представлены в виде точек на эллиптической кривой:

Получены они из постановки задачи в виде QAP при помощи необратимой операции умножения на эллиптической кривой с использованием токсичных параметров.
Теперь, когда начальные параметры созданы, мы можем начать работу с доказательствами. В нашем случае можно сгенерировать и проверить доказательство того, что известен корень уравнения (например, ). При этом доказательство не будет раскрывать значение секрета (корня уравнения) и будет состоять из нескольких точек эллиптической кривой.
Однако, в силу математики, лежащей в основе протокола, если токсичные параметры сохранились у кого-то после церемонии, этот человек сможет доказывать ложные факты. Возвращаясь к нашему примеру, можно доказать, что 2 является корнем уравнения, хотя это, очевидно, не так.
Вторая опасность заключается в том, что можно намеренно оставить лазейку (backdoor) в постановке задачи. А именно, можно получить начальные параметры из уравнения:
В таком случае все честные участники будут играть по правилам: решать уравнение , а злоумышленник будет использовать лазейку — корень многочлена , и никто даже не догадается об этом. Ведь после церемонии система оперирует лишь публичными (доверенными) параметрами, которые получены при помощи необратимой операции умножения на эллиптической кривой. И следовательно, без публикации токсичных параметров (что абсурдно) невозможно проверить подлинность задачи, для который формируются доказательства.
Такого рода backdoor открывает участникам церемонии безграничные возможности для манипуляции системами, использующими zk-SNARK протоколы. Рассмотрим для примера систему, которая оперирует аккаунтами пользователей с различными правами (в криптовалютах аккаунт — это публичный ключ, а управлять средствами на нём может лишь обладатель соответствующего приватного ключа). Пусть система приватная, и факт владения аккаунтом (обладание приватным ключом в случае криптовалюты) доказывается с помощью zk-SNARK протокола. Тогда задача должна быть сформулирована так: “Доступ к аккаунту Y может получить тот, кто предоставит соответствующий приватный ключ X”.
Однако, если в ходе генерации доверенных параметров она будет сформулирована так: "Доступ к аккаунту Y может получить тот, кто предоставит соответствующий приватный ключ X или число 13", то участники церемонии, знающие секретное число 13, смогут получить доступ к аккаунту любого пользователя (доступ к средствам, если это криптовалюта).
В заключение стоит отметить, что критичность церемонии и вытекающих из неё угроз следует рассматривать отдельно для каждой конкретной системы. И в то же время, для всех систем, использующих SNARK протоколы, необходима надежная процедура генерации начальных параметров с гарантиями подлинности решаемой задачи и уничтожения токсичных параметров.
Комментарии (6)

eup
28.12.2018 20:32+4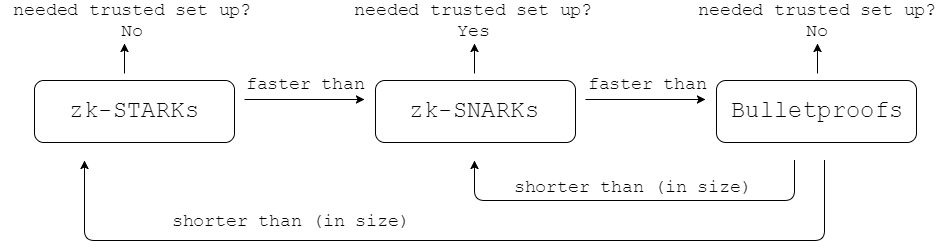
На смену zk-SNARKs и STARKs уже приходят Bulletproofs (можно найти в Monero, Grin), такие же не интерактивные док-ва с нулевым разглашением, но которые при этом не требуют установки доверенных параметров, избавляя всех от паранойи. В проекте bulletproofs-dalek вообще скоро реализуют возможность помимо range proof генерировать доказательства для любой заранее заданной R1CS, как это сейчас позволяют делать zk-SNARKs, для любых арифметических цепей.


Disasm
Насколько я помню, в zk-SNARK доказательство нельзя построить без уравнения (или, если точнее, то системы ограничений), а значит, это уравнение известно всем. Что мешает проверить, что оно получено из "честного" исходного кода?
Кроме того, в отличие от оригинальной идеи zk-SNARK, в Zcash применён распределённый алгоритм генерации начальных параметров, который призван исключить ситуацию с сохранением "токсичных" данных (если только все участники генерации не окажутся "предателями").
DryginAlexander Автор
По первой части:
Тё доказательство строится на основе публичных параметров (известных всем), но это не исходная задача.
По второй: действительно, в Zcash используется распределённый алгоритм генерации (церемония). Её безопастность/корректность это тема для отдельного исследования и соотвественно статьи. Выше лишь описываются проблемы, которые она должна решать.
Disasm
А вы смотрели, что входит в эти публичные параметры? Для генерации доказательства нужен prover key (про который мы ничего не можем сказать) и функция (уравнение) вместе с R1CS. Без функции вы не сможете сгенерировать подтверждающие значения для системы R1CS (ровно как и без самой R1CS). Так что мешает эту функцию проверить на соответствие исходной задаче?
DryginAlexander Автор
Все верно. Суть в том, что prover key получен из исходной задачи, и невозможно проверить, что задача, которая будет решаться при генерации доказательства, соответсвует исходной. Так как prover key получен из исходной по средствам необратимой операции умножения на эллиптической кривой с использованием токсичных параметров, те чтобы проверить нужны токсичные параметры — их очевидно нельзя раскрывать.
Disasm
Размер prover key непосредственно зависит от количества уравнений в системе R1CS. Как вы собираетесь генерировать prover key, который подойдёт и для этой системы и для другой?