Примечание. Сокращенный перевод, скорее пересказ своими словами.
UPD: как отметили в комментариях, примеры не идеальны. Автор не ищет лучшее решение задачи, его цель объяснить сложность алгоритмов «на пальцах».
Big O нотация нужна для описания сложности алгоритмов. Для этого используется понятие времени. Тема для многих пугающая, программисты избегающие разговоров о «времени порядка N» обычное дело.
Если вы способны оценить код в терминах Big O, скорее всего вас считают «умным парнем». И скорее всего вы пройдете ваше следующее собеседование. Вас не остановит вопрос можно ли уменьшить сложность какого-нибудь куска кода до n log n против n^2.
Выбор структуры данных зависит от конкретной задачи: от вида данных и алгоритма их обработки. Разнообразные структуры данных (в .NET или Java или Elixir) создавались под определенные типы алгоритмов.
Часто, выбирая ту или иную структуру, мы просто копируем общепринятое решение. В большинстве случаев этого достаточно. Но на самом деле, не разобравшись в сложности алгоритмов, мы не можем сделать осознанный выбор. К теме структур данных можно переходить только после сложности алгоритмов.
Здесь мы будем использовать только массивы чисел (прямо как на собеседовании). Примеры на JavaScript.
Возьмем массив из 5 чисел:
Допустим надо получить первый элемент. Используем для это индекс:
Насколько это сложный алгоритм? Можно сказать: «совсем не сложный — просто берем первый элемент массива». Это верно, но корректнее описывать сложность через количество операций, выполняемых для достижения результата, в зависимости от ввода (операций на ввод).
Другими словами: насколько возрастет кол-во операций при увеличении кол-ва входных параметров.
В нашем примере входных параметров 5, потому что в массиве 5 элементов. Для получения результата нужно выполнить одну операцию (взять элемент по индексу). Сколько операций потребуется если элементов массива будет 100? Или 1000? Или 100 000? Все равно нужна только одна операция.
Т.е.: «одна операция для всех возможных входных данных» — O(1).
O(1) можно прочитать как «сложность порядка 1» (order 1), или «алгоритм выполняется за постоянное/константное время» (constant time).
Вы уже догадались что O(1) алгоритмы самые эффективные.
Теперь давайте найдем сумму элементов массива:
Опять зададимся вопросом: сколько операций на ввод нам потребуется? Здесь нужно перебрать все элементы, т.е. операция на каждый элемент. Чем больше массив, тем больше операций.
Используя Big O нотацию: O(n), или «сложность порядка n (order n)». Так же такой тип алгоритмов называют «линейными» или что алгоритм «линейно масштабируется».
Можем ли мы сделать суммирование более эффективным? В общем случае нет. А если мы знаем, что массив гарантированно начинается с 1, отсортирован и не имеет пропусков? Тогда можно применить формулу S = n(n+1)/2 (где n последний элемент массива):
Такой алгоритм гораздо эффективнее O(n), более того он выполняется за «постоянное/константное время», т.е. это O(1).
Фактически операций не одна: нужно получить длину массива, получить последний элемент, выполнить умножение и деление. Разве это не O(3) или что-нибудь такое? В Bio O нотации фактическое кол-во шагов не важно, важно что алгоритм выполняется за константное время.
Алгоритмы с константным временем это всегда O(1). Тоже и с линейными алгоритмами, фактически операций может быть O(n+5), в Big O нотации это O(n).
Давайте напишем функцию которая проверяет массив на наличие дублей. Решение с вложенным циклом:
Мы уже знаем что итерирование массива это O(n). У нас есть вложенный цикл, для каждого элемента мы еще раз итерируем — т.е. O(n^2) или «сложность порядка n квадрат».
Алгоритмы с вложенными циклами по той же коллекции всегда O(n^2).
В примере выше, вложенный цикл, сам по себе (если не учитывать что он вложенный) имеет сложность O(n), т.к. это перебор элементов массива. Этот цикл заканчивается как только будет найден нужный элемент, т.е. фактически не обязательно будут перебраны все элементы. Но в Big O нотации всегда рассматривается худший вариант — искомый элемент может быть самым последним.
Здесь вложенный цикл используется для поиска заданного элемента в массиве. Поиск элемента в массиве, при определенных условиях, можно оптимизировать — сделать лучше чем линейная O(n).
Пускай массив будет отсортирован. Тогда мы сможем использовать алгоритм «бинарный поиск»: делим массив на две половины, отбрасываем не нужную, оставшуюся опять делим на две части и так пока не найдем нужное значение. Такой тип алгоритмов называется «разделяй и влавствуй» Divide and Conquer.
Этот алгоритм основан на логарифме.
Рассмотрим пример, чему будет равен x?
x^3 = 8
Нужно взять кубический корень от 8 — это будет 2. Теперь посложнее
2^x = 512
С использованием логарифма задачу можно записать так
log2(512) = x
«логарифм по основанию 2 от 512 равен x». Обратите внимание «основание 2», т.е. мы мыслим двойками — сколько раз нужно перемножить 2 что бы получить 512.
В алгоритме «бинарный поиск» на каждом шаге мы делим массив на две части.
Мое дополнение. Т.е. в худшем случае делаем столько операций, сколько раз можем разделить массив на две части. Например, сколько раз мы можем разделить на две части массив из 4 элементов? 2 раза. А массив из 8 элементов? 3 раза. Т.е. кол-во делений/операций = log2(n) (где n кол-во элементов массива).
Получается, что зависимость кол-ва операций от кол-ва элементов ввода описывается как log2(n)
Таким образом, используя нотацию Big O, алгоритм «бинарный поиск» имеет сложность O(log n).
Вернемся к задачке проверки массива на дубли. Мы перебирали все элементы массива и для каждого элемента еще раз делали перебор. Делали O(n) внутри O(n), т.е. O(n*n) или O(n^2).
Мы можем заменить вложенный цикл на бинарный поиск. Т.е. у нас остается перебор всех элементов O(n), внутри делаем O(log n). Получается O(n * log n), или O(n log n).
UPD: как отметили в комментариях, примеры не идеальны. Автор не ищет лучшее решение задачи, его цель объяснить сложность алгоритмов «на пальцах».
Big O нотация нужна для описания сложности алгоритмов. Для этого используется понятие времени. Тема для многих пугающая, программисты избегающие разговоров о «времени порядка N» обычное дело.
Если вы способны оценить код в терминах Big O, скорее всего вас считают «умным парнем». И скорее всего вы пройдете ваше следующее собеседование. Вас не остановит вопрос можно ли уменьшить сложность какого-нибудь куска кода до n log n против n^2.
Структуры данных
Выбор структуры данных зависит от конкретной задачи: от вида данных и алгоритма их обработки. Разнообразные структуры данных (в .NET или Java или Elixir) создавались под определенные типы алгоритмов.
Часто, выбирая ту или иную структуру, мы просто копируем общепринятое решение. В большинстве случаев этого достаточно. Но на самом деле, не разобравшись в сложности алгоритмов, мы не можем сделать осознанный выбор. К теме структур данных можно переходить только после сложности алгоритмов.
Здесь мы будем использовать только массивы чисел (прямо как на собеседовании). Примеры на JavaScript.
Начнем с самого простого: O(1)
Возьмем массив из 5 чисел:
const nums = [1,2,3,4,5];Допустим надо получить первый элемент. Используем для это индекс:
const nums = [1,2,3,4,5];
const firstNumber = nums[0];Насколько это сложный алгоритм? Можно сказать: «совсем не сложный — просто берем первый элемент массива». Это верно, но корректнее описывать сложность через количество операций, выполняемых для достижения результата, в зависимости от ввода (операций на ввод).
Другими словами: насколько возрастет кол-во операций при увеличении кол-ва входных параметров.
В нашем примере входных параметров 5, потому что в массиве 5 элементов. Для получения результата нужно выполнить одну операцию (взять элемент по индексу). Сколько операций потребуется если элементов массива будет 100? Или 1000? Или 100 000? Все равно нужна только одна операция.
Т.е.: «одна операция для всех возможных входных данных» — O(1).
O(1) можно прочитать как «сложность порядка 1» (order 1), или «алгоритм выполняется за постоянное/константное время» (constant time).
Вы уже догадались что O(1) алгоритмы самые эффективные.
Итерации и «время порядка n»: O(n)
Теперь давайте найдем сумму элементов массива:
const nums = [1,2,3,4,5];
let sum = 0;
for(let num of nums){
sum += num;
}Опять зададимся вопросом: сколько операций на ввод нам потребуется? Здесь нужно перебрать все элементы, т.е. операция на каждый элемент. Чем больше массив, тем больше операций.
Используя Big O нотацию: O(n), или «сложность порядка n (order n)». Так же такой тип алгоритмов называют «линейными» или что алгоритм «линейно масштабируется».
Анализ
Можем ли мы сделать суммирование более эффективным? В общем случае нет. А если мы знаем, что массив гарантированно начинается с 1, отсортирован и не имеет пропусков? Тогда можно применить формулу S = n(n+1)/2 (где n последний элемент массива):
const sumContiguousArray = function(ary){
//get the last item
const lastItem = ary[ary.length - 1];
//Gauss's trick
return lastItem * (listItem + 1) / 2;
}
const nums = [1,2,3,4,5];
const sumOfArray = sumContiguousArray(nums);Такой алгоритм гораздо эффективнее O(n), более того он выполняется за «постоянное/константное время», т.е. это O(1).
Фактически операций не одна: нужно получить длину массива, получить последний элемент, выполнить умножение и деление. Разве это не O(3) или что-нибудь такое? В Bio O нотации фактическое кол-во шагов не важно, важно что алгоритм выполняется за константное время.
Алгоритмы с константным временем это всегда O(1). Тоже и с линейными алгоритмами, фактически операций может быть O(n+5), в Big O нотации это O(n).
Не самые лучшие решения: O(n^2)
Давайте напишем функцию которая проверяет массив на наличие дублей. Решение с вложенным циклом:
const hasDuplicates = function (num) {
//loop the list, our O(n) op
for (let i = 0; i < nums.length; i++) {
const thisNum = nums[i];
//loop the list again, the O(n^2) op
for (let j = 0; j < nums.length; j++) {
//make sure we're not checking same number
if (j !== i) {
const otherNum = nums[j];
//if there's an equal value, return
if (otherNum === thisNum) return true;
}
}
}
//if we're here, no dups
return false;
}
const nums = [1, 2, 3, 4, 5, 5];
hasDuplicates(nums);//trueМы уже знаем что итерирование массива это O(n). У нас есть вложенный цикл, для каждого элемента мы еще раз итерируем — т.е. O(n^2) или «сложность порядка n квадрат».
Алгоритмы с вложенными циклами по той же коллекции всегда O(n^2).
«Сложность порядка log n»: O(log n)
В примере выше, вложенный цикл, сам по себе (если не учитывать что он вложенный) имеет сложность O(n), т.к. это перебор элементов массива. Этот цикл заканчивается как только будет найден нужный элемент, т.е. фактически не обязательно будут перебраны все элементы. Но в Big O нотации всегда рассматривается худший вариант — искомый элемент может быть самым последним.
Здесь вложенный цикл используется для поиска заданного элемента в массиве. Поиск элемента в массиве, при определенных условиях, можно оптимизировать — сделать лучше чем линейная O(n).
Пускай массив будет отсортирован. Тогда мы сможем использовать алгоритм «бинарный поиск»: делим массив на две половины, отбрасываем не нужную, оставшуюся опять делим на две части и так пока не найдем нужное значение. Такой тип алгоритмов называется «разделяй и влавствуй» Divide and Conquer.
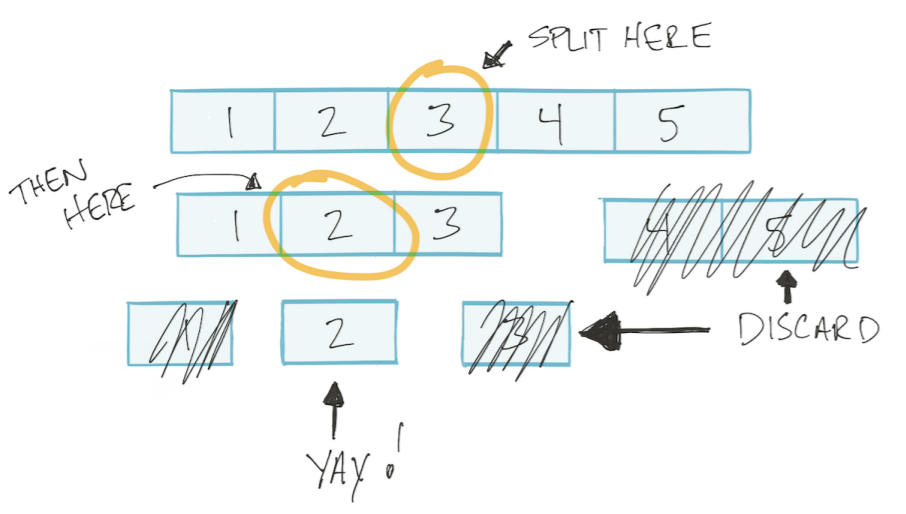
Этот алгоритм основан на логарифме.
Быстрый обзор логарифмов
Рассмотрим пример, чему будет равен x?
x^3 = 8
Нужно взять кубический корень от 8 — это будет 2. Теперь посложнее
2^x = 512
С использованием логарифма задачу можно записать так
log2(512) = x
«логарифм по основанию 2 от 512 равен x». Обратите внимание «основание 2», т.е. мы мыслим двойками — сколько раз нужно перемножить 2 что бы получить 512.
В алгоритме «бинарный поиск» на каждом шаге мы делим массив на две части.
Мое дополнение. Т.е. в худшем случае делаем столько операций, сколько раз можем разделить массив на две части. Например, сколько раз мы можем разделить на две части массив из 4 элементов? 2 раза. А массив из 8 элементов? 3 раза. Т.е. кол-во делений/операций = log2(n) (где n кол-во элементов массива).
Получается, что зависимость кол-ва операций от кол-ва элементов ввода описывается как log2(n)
Таким образом, используя нотацию Big O, алгоритм «бинарный поиск» имеет сложность O(log n).
Улучшим O(n^2) до O(n log n)
Вернемся к задачке проверки массива на дубли. Мы перебирали все элементы массива и для каждого элемента еще раз делали перебор. Делали O(n) внутри O(n), т.е. O(n*n) или O(n^2).
Мы можем заменить вложенный цикл на бинарный поиск. Т.е. у нас остается перебор всех элементов O(n), внутри делаем O(log n). Получается O(n * log n), или O(n log n).
const nums = [1, 2, 3, 4, 5];
const searchFor = function (items, num) {
//use binary search!
//if found, return the number. Otherwise...
//return null. We'll do this in a later chapter.
}
const hasDuplicates = function (nums) {
for (let num of nums) {
//let's go through the list again and have a
look
//at all the other numbers so we can compare
if (searchFor(nums, num)) {
return true;
}
}
//only arrive here if there are no dups
return false;
}Мышление в терминах Big O
- Получение элемента коллекции это O(1). Будь то получение по индексу в массиве, или по ключу в словаре в нотации Big O это будет O(1)
- Перебор коллекции это O(n)
- Вложенные циклы по той же коллекции это O(n^2)
- Разделяй и властвуй (Divide and Conquer) всегда O(log n)
- Итерации которые использую Divide and Conquer это O(n log n)
Комментарии (18)
khim
23.03.2019 03:33+1Может мне кто-нибудь объяснить что происходит в задаче с поиском дубликатов и с какого перепугу там вдруг взялся бинарный поиск?
Ведь бинарный поиск мы можем осуществлять только если элементы уже отсортированы — но в этом случае поиск дубликатов вообще осуществляется одним проходом и никакой бинарный поиск никому и даром не нужен…
Так-то если данные не отсортированы мы можем отсортировать их (уже потратив минимум O(n log?n), но потом найдя все дубликаты линейным проходом…
Mingun
23.03.2019 08:04+1Там просто пример некорректный. А так-то, осуществляя сортировку можно параллельно выкидывать дубликаты, т.е. сложность будет такая же, как от сортировки — потому что для нахождения дубликата нужно лишь посмотреть на соседа, что
O(1).
Вот кстати, к слову о нормальных инженерах: хотите быть нормальным инженером — прежде, чем применить алгоритм, проверьте его область применимости.
Alex_BBB Автор
23.03.2019 08:32Возможно пример не идеальный. Тут автор не ищет лучшее решение — его цель объяснить сложность алгоритмов «на пальцах». Думаю у него получилось.
Кстати подсчет суммы короче можно записать
const sumContiguousArray = function(ary){ //Gauss's trick return ary.length * (ary.length + 1) / 2; } const nums = [1,2,3,4,5]; const sumOfArray = sumContiguousArray(nums);ChePeter
23.03.2019 13:00это не короче. И запись кода длиннее и операций сложения столько же.
для последовательности в 8 чисел получится 4+2+1 = 7 операций
в общем случае для подсчета суммы 2^n чисел потребуется 2^n-1 операций сложения
khim
23.03.2019 18:30Тут автор не ищет лучшее решение — его цель объяснить сложность алгоритмов «на пальцах». Думаю у него получилось.
У него получилось сделать бяку. Как в анекдоте «а о том, как выйти из штопора, смотрите в следующем номере».
Импринтинг — он не только у причек бывает. Человек — тоже склонен использовать то, что он когда-то увидел первый раз. И если человек про Big O не знает — то этот пример легко может запасть ему в душу. И он потом будет вкручивать этот бинарный поиск где нужно и где не нужно.
Atos
23.03.2019 10:01Разделяй и властвуй (Divide and Conquer) всегда O(log n)
Итерации которые использую Divide and Conquer это O(n log n)
Серьёзно??
Зачем переводить дилентантские высказывания о теории сложности?
Декомпозиция (Divide and Conquer) — это одна из общих парадигм разработки алгоритмов. Логарифм при её использовании действительно появляется часто, но отнюдь не всегда, вообще говоря, вычислительная сложность может быть любой, от O(logN) и выше (как, скажем, в примере с умножением матриц за O(N^(2+?)), который тут приводили). См. Основную теорему о рекуррентных соотношенияхAtos
23.03.2019 17:11Как раз выложил пример — Пятнашки глазами алгоритмиста. Часть 4 с половиной: демоны и декомпозиция
third112
23.03.2019 16:28Про самое интересное и драматичное — экспоненциальные алгоритмы не сказали.
khim
23.03.2019 18:15О да. Помню я одну из книжек про Пролог. Где объясняли как написать программу проверяющую, отсортированы ли данные и программу, порождающую все перестановки. А потом объединяешь их — и хопа: алгоритм сортировки.
Я прям порадовался: это ж кем надо быть, чтобы такое породить-то? И да, создатели этого идиотизма — тогда потом отнекивались, что они не хотели показать читателям ничего плохого, хотели просто показать как Prolog может «обратную задачу» решать.
SirEdvin
Пожалуйста, если вы хотите быть нормальным инженером, никогда не мыслите в терминах big-O, реальные системы это не асимптоматика:
Хотя бы бенчмарки проводите параллельно.
kzhyg
Если вы хотите быть нормальным инженером, никогда не говорите "это не работает", увидев один контраргумент.
BugM
Реальный код это как раз асимптоматика в большинстве случаев. Умножения матриц пишут редко, а «работает и ладно» постоянно.
Перебор коллекции внутри перебора другой коллекции есть прям везде. Особенно сложные лямбды этим грешат. Почти всегда можно что-нибудь посортировать или вообще в мапу переложить. Код становится быстрее в разы.
Collection.indexof можно в 95% случаев переписать. Аналогично становится быстрее в разы.
Прикрутить дерево для изменяемого сортированного списка уже сложнее, но выигрыш и тут в разы.
И не важно как там реализовано. Все коллизии и прочие n^2.3727 теряются по сравнению с изменением алгоритма.
SirEdvin
А вы точно понимаете, что такое "асимптоматика"? В реальном коде у вас всегда n ограничено сверху. Более того, часто оно ограничено сверху насколько сильно, что превращяется в вырожденный случай. Например, для корзины товаров это вполне может быть n < 3. А в таких случаях все эти оценки очень сильно сбоят, потому что более продвинутые алгоримты, обычно, имеют куда большую константу.
Будет ли оптимальнее менять сортированный список на бинароное дерево в таком случае? Я думаю, что очень сомнительно.
khim
Кстати, тот самый алгоритм, которым вы всех пугаете, умножение матриц, вовсе не так страшен, как вы говорите. Вот именно классически, в Big O. Потому что да, он O(N?)… вот только N — это не размер матрицы! Размер матрицы (сколько она в памяти занимает) — это N?. То есть реально ваш ужасный, кошмарный, ай-ай-ай какой алгоритм — это O(size1?)… не так и много. Когда мы от всех O(N?) избавились — можно уже и константе подумать, да… но это — уже второй этап! Первый — это именно ассимптотика.
P.S. И да, конечно, далеко не всегда нужно от Big O избавляться, тут вы правы. У меня на работе есть программка, где алгоритм работает за время O(N?), где N — это таки реально размер задачи. Вот только это N… оно было равно 8 в 1978м году, 16 в 1985м, но 32 — только в 2012м… и не факт, что в ближайшие лет 20 это число вырастет ибо новые архитектуры с большим числом регистров раждаются нечасто. Но это — скорее исключение из правил.
SirEdvin
Нет. До железа у вас есть ограничения исходят от бизнес-правил/задачи. Вы же не берете наборы чисел и списки из воздуха. Обычно это список чего-то, вещей в корзине, платежей, задач в таск трекере и так далее. И очень часто оказывается, что ограничение довольно жесткое, иногда доходящее до "не больше 2".
И снова нет. Я не зря упомянул перемножение матрицы (я думал все знают, что обсуждая сложность перемножение матрицы все подразумевают, что она квадратная, с размерностью n), потому что этот пример как можно лучше демонстрирует то, что константа крайне важна.
Есть как бы три известных алгоримта, наивная реализация со сложностью O(n^3), Алгоритм Штрассена, который имеет сложность O(n^2.81) и Алгоритм Копперсмита — Винограда который имеет сложность O(n^2.3727). Казалось бы, надо брать последний и радоватся, да?
На практике же, последний не используется совсем из-за очень большой константы, а алгоритм Штрассена не используется для матриц размерностью больше 64 в силу той же константы.
Поэтому, когда вы говорите, что "первый этап — это асимптотика", вы ошибаетесь. Первый этап — это нахождение ограничений, которые накладываются задачей. Если вы анализируете алгоритм без этого этапа, вы практически всегда сделаете это неправильно. А вот вторым этапом уже может быть подбор алгоримта с учетом этих ограничений.
khim
И много вы видели багтрекеров с максимум двумя багами или корзину с не более, чем двумя товарами?
В моей практике как раз наоборот: гораздо чаще люди предполагают, что у них может быть, скажем, 100 человек на избирательном участке, а когда им, в результате того, что где-то данные посчитали вручную, приходит информации о голосовании ста тысяч человек человек (просто руками объединённые данные о нескольких удалённых участках), то это кладёт нафиг всю их систему голосования. Пример вполне из жизни, кстати.
И все три они — ближе к линейному алгоритму, чем к сортировке пузырьком. Но главное даже не в этом.
Вот вы тут рассусоливаете про «количество вещей в корзине, платежей, задач в таск трекере» — а как часто вы всё это засовываете в матрицы, которые затем перемножаете? Ну, в сравнении с кодом, который обнаруживает дубликаты и их объединяет, сортирует там по разному и тому подобными «банальностями», где вы можете получить O(N?) вместо O(N log N), если не подумать?
В моей практике на одно место, где кто-то использует ассимптотически хороший алгоритм с огромной константой приходятся десятки мест, где кто-то сортирует пузырьком или ищет дубликаты двумя вложенными циклами.
Вот когда избавитесь от этих тривиальных проблем — тогда и можно будет говорить об алгоримте Штрассена и перемножении матриц…
BugM
Возьмем магазин автозапчастей. Внезапно, у нас корзина на сотню товаров становится нормальной. И софт сделанный под корзины в 2-3 товара будет тормозить на очень критичных операциях. Минус клиенты, минус прибыль.
Я не рассматривал крайние случаи. Понятно что они есть и встречаются в реальной жизни. Но в среднем более быстрый асимптоматически алгоритм будет лучше. Любой другой случай это скорее исключение и когда его используешь надо четко понимать что делаешь и подробно комментировать и документировать все это. А для этого надо знать сложность алгоритмов, Big O вот это вот все.