15.05.2019 09:03
dm_p2016 4 3500 Источник
В одном из проектов, над которыми мне довелось работать, был реализован механизм обмена данными между удалёнными компонентами системы, работавший по следующему сценарию: компонент-источник А на своей стороне подготавливает данные, предназначенные для передачи; компонент-получатель Б периодически открывает сеанс связи и забирает все данные, которые накопил А на момент подключения. Данные, поступающие уже в во время сеанса связи, откладываются до следующего подключения.

В какой-то момент я понял, что передача данных в такой схеме описывается с помощью обыкновенного дифференциального уравнения. Описание модели и выводы, которые удалось получить с её помощью, под катом.

Обозначим $x(t)$ — объем данных в некоторых условных единицах, накопленных для обмена на стороне компонента А к моменту времени $t$. Пусть пауза между завершением сеанса обмена и началом следующего равна $a_0>0$ единиц времени, а для передачи одной единицы данных требуется $a_1>0$ единиц времени. Тогда на передачу $x(t)$ единиц данных требуется $a_0 + a_1x(t)$ единиц времени. Скорость передачи данных равна

$\frac{x(t)}{a_0+a_1x(t)}.\quad (1)$


Если скорость накопления данных на стороне А обозначить $f(t)$, то $x(t)$ является решением дифференциального уравнения:

$\frac{dx}{dt}=-\frac{x}{a_0+a_1x}+f(t).\quad (2)$


Так как неограниченный рост объёма ещё непереданных данных является крайне нежелательной ситуацией, то важной задачей становится получение условий ограниченности решений этого уравнения.

Для простоты будем считать функцию $f(t)$ непрерывной. Пусть

$f(t)=\phi_0 + \phi(t),$


где

$\left|\int_0^t\phi(s)ds\right| \leq K_{\phi} < +\infty$


при всех $t\geq 0$, а $\phi_0>0$ — постоянная, играющая роль среднего значения.

Рассмотрим несколько примеров. Пусть $f(t)$ периодическая и её график имеет вид:

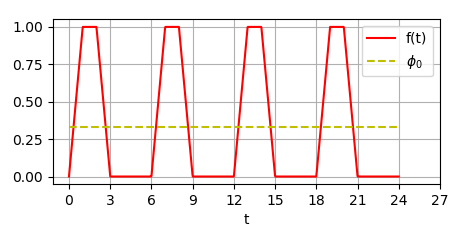
image

В этом случае $\phi_0=1/3$, $\phi(t) = f(t) - \phi_0$.
Численно проинтегрировав уравнение (1) для нескольких значений параметров $a_0, a_1$ и начальных значений $x(0)$, получим следующие графики решений:
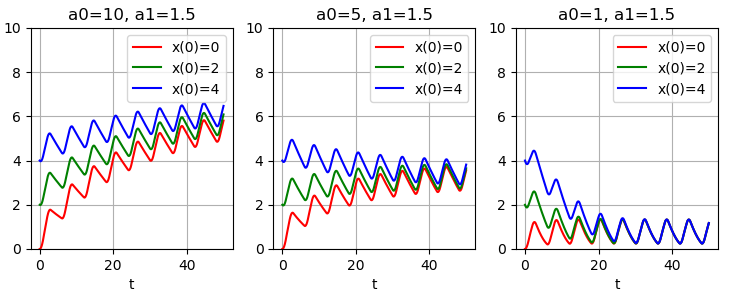
image

image

Из примеров видно: когда $1/a_1 > \phi_0$, решения ограничены и при различных значениях $x(0)$ система стремится к некоторому установившемуся режиму. Чем меньше длительность пауз между сеансами $a_0$, тем эта сходимость быстрее. При $1/a_1 < \phi_0$ такой сходимости не наблюдается, а решения с течением времени растут. Уменьшение длительности пауз замедляет скорость роста, но тенденция к неограниченному возрастанию $x(t)$ всё равно сохраняется.

В общем случае можно показать, что если $1/a_1 > \phi_0$, то решения уравнения (1) ограничены, а если $1/a_1 < \phi_0$ — будут получаться неограниченные решения. То есть ограниченность решений определяется только соотношением скоростей накопления и извлечения данных. Длительность пауз между сеансами обмена $a_0$, единственный параметр, которым можно легко управлять, принципиально не влияет на поведение системы. Хотя, как видно из соотношения (1) и примеров, с её увеличением скорость обмена уменьшается.

В итоге анализ модели позволяет сделать следующие выводы. Если скорость обмена оказывается недостаточной, и на стороне источника постоянно растёт объём данных для отправки, то пытаться исправить ситуацию уменьшением пауз между сеансами не имеет смысла. Помочь здесь может только увеличение производительности системы.

С другой стороны, в случае когда сервис обмена постоянно загружает компьютеры в ущерб другим задачам, верным решением будет рекомендовать увеличить в разумных пределах продолжительность пауз: это повлияет только актуальность данных, без риска переполнения источника неотправленными данными.

Подробные выкладки для условий ограниченности решений и некоторые другие вопросы, касающиеся рассмотренной модели, опубликованы в материалах школы-семинара ”Математическое моделирование, численные методы и комплексы программ” имени Е.В. Воскресенского. Посмотреть и скачать статью можно по этой ссылке.

Комментарии (4)


  1. lynxus
    15.05.2019 17:09
    #20157140

    диффуры как то подразумевают ещё один вариант решения :)

    можно попробовать предавать дельту:
    когда получатель не забрал старую дельту, то источник просто добавляет к ней новую

    если можно перевести данные в дельты, конечно…


  1. AC130
    16.05.2019 07:21
    #20159104

    Если скорость обмена оказывается недостаточной, и на стороне источника постоянно растёт объём данных для отправки, то пытаться исправить ситуацию уменьшением пауз между сеансами не имеет смысла.

    Вроде для этого вывода модель с дифференциальными уравнениями не нужна? На крайний случай можно было бы рассмотреть условие dx\dt < 0 (что есть ненакопление объёма данных на источнике), сократить дробь для скорости передачи данных на x, максимизировать по a0 (решение a0=0) и у вас получается та же самая граница 1/a1 > phi0


    1. dm_p2016 Автор
      16.05.2019 14:27
      #20161160

      Дифференциальное уравнение всё же неявно здесь подразумевается: ведь рассуждения строятся на равенстве скоростей dx/dt = -x/(xa_1 + a_0) + f(t). Только не записано само уравнение.

      В общем случае использовать для ограниченности критерий dx/dt < 0 нельзя: на одних участках x(t) может убывать, на других — возрастать. А x(t) при этом может быть как ограниченной, так и неограниченной.

      Если принять a0=0, то сократить на x в общем случае тоже нельзя, так как x может оказаться равным нулю. Если это проигнорировать, то получится, что мы что-то забираем с постоянной скоростью, даже когда данных нет, x(t) станет отрицательным.

      Рассуждения, использовавшиеся при получении вывода о неограниченности решений при 1/a1 < phi_0, в чем-то схожи с вашей идеей.
      Запишем дифур и воспользуемся тем, что x/(xa_1 + a_0) возрастает по x. Тогда
      dx/dt = -x/(xa_1 + a_0) + f(t) > -1/a_1+\phi_0 + \phi(t) > c + \phi(t),
      где c > 0. Откуда вытекает, что x(t) >= ct + const.

      Для доказательства ограниченности при условии 1/a1 > phi_0 потребовались более сложные методы.


  1. amarao
    17.05.2019 18:35
    #20167628

    Не убедили. То, что вы говорите, и так 101 тюнинга. Точнее, 102 тюнинга, потому что 101 тюнинга говорит, что если вы делаете тюнинг не из экономических или спортивных интересов, то ваша архитектура — г-но.


    Кстати, в вашей матмодели не учтены накладные расходы на отправку — слишком частый поллинг может начинать сам по себе есть много ресурсов.