Вселенная задач, проверяемых компьютером, выросла. Благодаря какому секретному ингредиенту это произошло? Из-за квантовой запутанности.

Представьте, что некто пришёл к вам и заявил, что у него есть оракул, способный раскрыть сокровенные тайны вселенной. Вы могли бы заинтересоваться этим, но вам тяжело было бы в это поверить. Вы бы хотели придумать способ подтвердить, что оракул говорит правду.

Такова основная проблема информатики. Некоторые задачи слишком сложно решить за разумное время. Но их решения просто проверить. Учитывая это, специалистам по информатике хочется знать: насколько сложной может быть задача, решение которой всё ещё можно проверить?

Оказывается, что ответ на этот вопрос: практически невообразимо сложной.

В работе, появившейся в апреле 2019, два специалиста по информатике радикально увеличили количество задач, попадающих в категорию «сложно решить, легко проверить». Они описывают метод, позволяющий проверять решения задач практически непостижимой сложности. «Звучит безумно», — сказал Томас Видик, специалист по информатике из Калифорнийского технологического института, не связанный с данной работой.

Исследование применимо к квантовым компьютерам, проводящим вычисления согласно неинтуитивным правилам квантовой механики. Квантовые компьютеры едва появились, но в будущем у них есть потенциал провести революцию в области вычислений.

Новая работа, по сути, даёт нам рычаг влияния на того всемогущего оракула. Даже если оракул обещает дать вам готовые решения задач, возможности решения которых находятся далеко за пределами ваших способностей, всё равно остаётся способ проверить, говорит ли оракул правду.

До конца вселенной

Когда задачу сложно решить, но легко проверить, поиск решения требует длительного времени, но проверка правильности конкретного решения – не требует. К примеру, представим, что человек показывает вам граф – набор точек (вершин), соединённых линиями (рёбрами). Человек спрашивает, можно ли раскрасить вершины графа тремя цветами так, чтобы ни у каких двух соединенных вершин не было одного цвета.



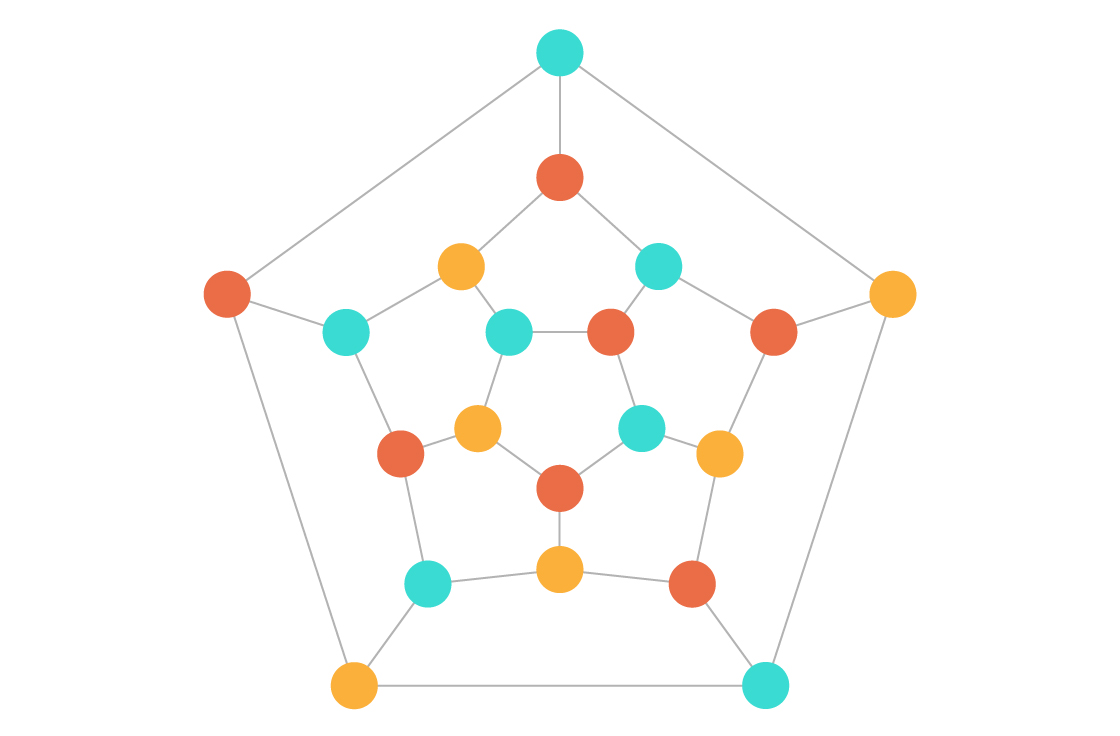
Задачу трёх цветов решить сложно. В общем случае время, необходимое на поиски раскраски вершин (или определение, что такой раскраски не существует) увеличивается экспоненциально при увеличении размера графа. Если, допустим, поиск решения для графа с 20 вершинами занимает 3²⁰ нс – то есть, несколько секунд, то для графа с 60 вершинами на поиски уйдёт уже 3⁶⁰ нс, что в 100 раз больше текущего возраста Вселенной.

Но, допустим, некто утверждает, что раскрасил граф тремя цветами. На проверку этого заявления не уйдёт много времени. Нужно просто обойти все вершины по одной, изучая связанные с ними вершины. С увеличением размера графа время этой проверки увеличивается медленно – как полиномиальное. В итоге у компьютера на проверку раскраски графа из 60 вершин уходит не сильно больше времени, чем на проверку графа из 20 вершин.

«При правильной раскраске тремя цветами легко проверить её работоспособность», — сказал Джон Райт, физик из Массачусетского технологического института, писавший эту работу совместно с Анандом Натараджаном из Калтеха.

В 1970-х специалисты по информатике определили класс задач, которые легко проверить, даже если некоторые из них сложно решить. Они назвали этот класс NP, недетерминированное полиномиальное время. С тех пор в информатике класс NP изучали больше других. В частности, специалисты по информатике хотели бы знать, как меняется этот класс, когда проверяющий алгоритм получает новые способы проверки правильности решения.

Правильные вопросы

До работы Натараджана и Райта мощность проверок возрастала двумя большими скачками.

Чтобы понять первый из них, представьте, что вы не различаете цветов. Некто размещает перед вами на столе два кубика, и спрашивает, одного они цвета или разных. Для вас эта задача оказывается невозможной. Более того, вы не можете подтвердить правильность чужого решения этой задачи.

Однако вам разрешено задавать этому человеку, доказывающему, вопросы. Допустим, доказывающий говорит вам, что кубики разных цветов. Вы называете один из них «кубик А», а другой – «кубик Б». Затем вы прячете их за спину, и случайно меняете между собой местами. Потом вы открываете кубики и просите доказывающего найти кубик А.

Если кубики разных цветов, это очень простой вопрос. Доказывающий узнает кубик А, если это, допустим, красный кубик, и будет правильно определять его каждый раз.

Однако, если кубики одинаковых цветов – и доказывающий ошибся, назвав их разными – доказывающий сможет лишь догадываться, какой из них какой. Поэтому он сможет правильно определять кубик А лишь в 50% случаев. Постоянно опрашивая доказывающего об его решении, вы сможете подтвердить, правильное ли оно.


Ананд Натараджан и Джон Райт

«Проверяющий может отправлять доказывающему вопросы, — сказал Райт, — и, возможно, в конце разговора проверяющий будет более убеждён в ответе».

В 1985 году три специалиста по информатике доказали, что подобные интерактивные доказательства можно использовать для подтверждения решения более сложных задач, чем задачи из NP. Их работа создала новый класс задач, IP, «интерактивное полиномиальное время». Метод, использованный для подтверждения цветов кубиков, можно использовать для подтверждения ответов на гораздо более сложные вопросы.

Второй прорыв произошёл в том же десятилетии. Он похож на логику полицейского расследования. Если у вас есть двое подозреваемых, совершивших, по вашему мнению, преступление, вы не будете допрашивать их вместе. Вы допросите их в разных комнатах, и будете сверять ответы одного с ответами другого. Опрашивая их по отдельности, вы сможете раскрыть больше правды, чем если бы у вас был один подозреваемый.

«У двух подозреваемых не получится сформировать распределённую непротиворечивую историю, поскольку они не знают, какие ответы даёт другой», — сказал Райт.

В 1988 году четыре специалиста по информатике доказали, что если попросить два компьютера отдельно решить одну и ту же задачу – и потом допросить по поводу ответов отдельно – можно подтвердить класс проблем, даже больший, чем IP: класс MIP, интерактивные доказательства со множеством доказывающих.

Используя такой подход, можно, к примеру, подтвердить правильность раскраски графа в три цвета для последовательности графов, увеличивающихся в размерах гораздо быстрее, чем графы из NP. В NP размеры графов увеличиваются линейно – количество вершин может расти от 1 до 2, до 3, до 4, и так далее – так, чтобы размер графа не был непропорционально больше количества времени, необходимого для проверки раскраски. Но в MIP количество вершин графа растёт экспоненциально от 2¹ до 2², 2³, 2⁴, и так далее.

В итоге графы оказываются слишком большими даже просто для того, чтобы поместиться в памяти компьютера, который должен пройтись по списку вершин и проверить раскраску. Однако раскраску всё равно можно проверить, задав двум доказывающим разные, но связанные между собой вопросы.

В MIP у проверяющего есть достаточно памяти для запуска программы, позволяющей нам определить, соединены ли две вершины графа ребром – и он может сверить ответы доказывающих, чтобы убедиться в правильности раскраски.

Расширением списка задач, которые сложно решить, но легко проверить, с NP до IP и MIP занимались классические компьютеры. Но квантовые компьютеры работают совсем по-другому. И несколько десятилетий было непонятно, как их использование меняет эту картину – облегчается, или усложняется проверка решений с их помощью?

В новой работе Натараджана и Райта есть ответ на этот вопрос.

Квантовые трюки

Квантовые компьютеры проводят вычисления, орудуя квантовыми битами, или кубитами. У них есть такое свойство, как запутанность друг с другом. И когда два кубита – или даже крупные системы кубитов – запутаны, это значит, что их физические свойства определённым образом влияют друг на друга.

В своей новой работе Натараджан и Райт рассматривают сценарий, в который входят два разных квантовых компьютера, причём кубиты одного запутаны с кубитами другого.

Казалось бы, подобная установка ухудшает качество проверки ответов. Вся сила интерактивных доказательств со множеством доказывающих проистекает именно из того факта, что вы можете опрашивать двух доказывающих по отдельности, и сверять их ответы. Если ответы доказывающих совпадают, то они, скорее всего, верны. Но если квантовые состояния двух доказывающих запутаны, у них, казалось бы, будет больше возможностей непротиворечиво настаивать на правильности неверных ответов.

Действительно, когда сценарий с двумя запутанными квантовыми компьютерами впервые был обнародован в 2003 году, специалисты по информатике предположили, что запутанность уменьшит возможности проверки. «Очевидной реакцией всех, и моей в том числе, было то, что у доказывающих в таком случае больше возможностей, — сказал Видик. – Они могут использовать запутанность, чтобы связывать свои ответы».

Но, несмотря на изначальный пессимизм, Видик несколько лет провёл в попытках доказать обратное. В 2012 году он и Tсуйоши Ито доказали, что возможность проверить все задачи в MIP при помощи запутанных квантовых компьютеров существует.

А теперь Натараджан и Райт доказали, что ситуация даже ещё лучше: при помощи запутанности можно доказать даже ещё более крупный класс задач, чем без неё. Можно обратить связь между запутанными квантовыми компьютерами на пользу проверяющему.

Чтобы понять, как это сделать, вспомним процедуру из MIP для проверки раскраски графов, чьи размеры растут экспоненциально. У проверяющего не хватит памяти для хранения графа целиком, но у него достаточно памяти для определения двух связанных вершин, и для того, чтобы задать проверяющим вопрос о цвете этих вершин.

В классе задач, рассматриваемых Натараджаном и Райтом – под названием NEEXP, недетерминистское дважды экспоненциальное время – размеры графов растут ещё быстрее, чем в MIP. Графы в NEEXP растут с «дважды экспоненциальной скоростью». Вместо того, чтобы расти, как степени двойки — 2¹, 2², 2³, 2⁴, и так далее – количество вершин в графах растёт, как степени степени двойки — 2²¹, 2²²,2²³,2²⁴, и так далее. В итоге графы быстро получаются настолько огромными, что проверяющий уже даже не способен найти пару соединённых вершин.

«Для идентификации вершины необходимо 2ⁿ битов, что экспоненциально больше, чем есть у проверяющего в памяти», — сказал Натараджан. Однако Натараджан и Райт доказали, что возможно проверить раскраску дважды экспоненциального графа в три цвета, даже без возможности определить, о каких вершинах нужно задавать вопросы доказывающим. Дело в том, что можно заставить доказывающих самих выбрать правильные вопросы.

Идея о том, чтобы заставить компьютеры допрашивать самих себя об их собственных решениях, для специалистов по информатике звучит примерно так же разумно, как просить подозреваемых в преступлениях допрашивать самих себя – определённо ведь глупое предложение. Вот только Натараджан и Райт доказали, что это не так. И причиной тому – запутанность.

«Запутанные состояния – это общие ресурсы, — сказал Райт. – Весь наш протокол состоит в том, чтобы понять, как использовать этот общий ресурс для создания взаимосвязанных вопросов».

Если квантовые компьютеры запутаны, то их выбор вершин будет коррелировать, и выдавать как раз нужный набор вопросов для проверки раскраски в три цвета.

В то же время, проверяющему не нужно, чтобы два квантовых компьютера были переплетены настолько, чтобы их ответы на эти вопросы коррелировали между собой (это было бы похоже на то, как двое подозреваемых в преступлении коррелируют свои ложные алиби). Этой проблемой занимается ещё одна странная квантовая особенность. В квантовой механике принцип неопределённости запрещает нам одновременно точно знать местоположение и момент частицы – если вы измеряете одно свойство, то уничтожаете информацию о другом. Принцип неопределённости строго ограничивает ваши знания о двух любых «дополняющих» свойствах квантовой системы.

Натараджан и Райт пользуются этим в своей работе. Чтобы вычислить цвет вершины, они заставляют два квантовых компьютера проводить дополняющие измерения. Каждый компьютер вычисляет цвет собственной вершины, и таким образом уничтожает всю информацию о другой. Иначе говоря, запутанность позволяет компьютерам выдавать коррелирующие вопросы, но принцип неопределённости запрещает им участвовать в сговоре при ответе на них.

«Нужно заставить доказывающих забыть, и это главное, что Натараджан и Райт сделали в своей работе, — сказал Видик. – Они заставляют доказывающего стереть информацию через проведение измерения».

Последствия их работы можно назвать практически экзистенциальными. До выхода работы ограничение на знание, которое мы можем получить с полной уверенностью, было гораздо меньшим. Если бы нам дали ответ на задачу из множества NEEXP, нам бы пришлось лишь принять его на веру. Но Натараджан и Райт вырвались за эти границы, и сделали возможным подтверждение ответов из куда как более обширной вселенной вычислительных задач.

И теперь, когда они это сделали, неясно, где лежит следующая граница проверяемости. «Она может оказаться гораздо дальше, — сказал Ланс Фортнау, специалист по информатике из Технологического института в Джорджии. – Они оставляют открытой возможность сделать следующий шаг».