Наткнулся на интересную задачку: Дано действительно число a и натуральное число n. Вычислите корень n-ой степени из числа без использование библиотек.
Входные данные: число a — действительное, неотрицательное, не превосходит 1000, задано с точностью до 6 знаков после запятой. Число n — натуральное, не превосходит 10.
Выходные данные: Программа должна вывести единственное число: ответ на задачу с точностью не менее 5 знаков после запятой.
Естественно было интересно решить её на черновике карандашом, а потом начеркать в редакторе и попробовать скомпилировать. Без гугления, подсказок и тем более использования библиотек. Если вы решаете такое в первый раз, то попробуйте сначала написать программку для нахождения обычного квадратного корня. Если вам кажется задача сложной, решите почти такую же, но попроще. Тогда у вас уйдет страх и возникнет какое-то примерное понимание.
Так что для начала я приведу пример того, как можно вычислить квадратный корень, не используя библиотечную функцию. Алгоритм последовательной итерации. Сходится довольно быстро даже для больших чисел.
/* Calculating the square root by iterations */
#include <stdio.h>
int main(void) {
double num = 570.15;
double root = num / 2;
double eps = 0.01;
int iter = 0;
while( root - num / root > eps ){
iter++;
root = 0.5 * (root + num / root);
printf("Iteration: %d : root = %f\n", iter, root);
}
printf("root = %f", root);
return 0;
}
Запустить код можно тут: КЛИК
Логарифмическая сложность алгоритма? Или другая? :)
Теперь уже можно переходить к усложненному варианту задачи. В этом случае решение получается более обобщенным.
#include <stdio.h>
double mabs(double x){ return (x < 0)? -x : x; }
int main(void) {
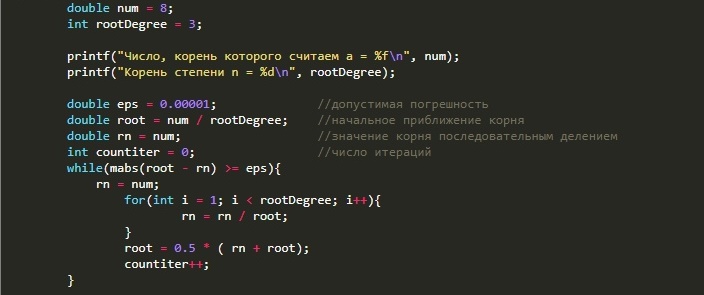
double num = 8;
int rootDegree = 3;
printf("Число, корень которого считаем а = %f\n", num);
printf("Корень степени n = %d\n", rootDegree);
double eps = 0.00001; //допустимая погрешность
double root = num / rootDegree; //начальное приближение корня
double rn = num; //значение корня последовательным делением
int countiter = 0; //число итераций
while(mabs(root - rn) >= eps){
rn = num;
for(int i = 1; i < rootDegree; i++){
rn = rn / root;
}
root = 0.5 * ( rn + root);
countiter++;
}
printf("root = %f\n", root);
printf("Число итераций = %i\n", countiter);
return 0;
}
Запустить код можно тут: КЛИК
В данном решении я использую идею относительно неплохого начального приближения. Затем последовательным делением находится второе приближение корня n-ой степени. Далее считается новое приближение с помощью усреднение двух текущих. Последовательно алгоритм сходится к нужному корню с наперед заданной погрешностью. Это немного похоже на метод простой итерации.
Это первый рабочий алгоритм, написанный на коленке. Нужно еще поразмышлять о сложности и возможностях ускорения. Кстати, какие возможности ускорения этого алгоритма можно реализовать на ваш взгляд?
Чувствую, что будет вопрос: «Зачем это делать, если всё реализовано в библиотеках сто лет назад?!»
Ответ: Лично мне всегда нравилось думать над алгоритмами, которые уже реализованы в стандартных библиотеках. Пытаться разработать их самостоятельно (ну или разработать какую-нибудь медленно работающую пародию и потерпеть неудачу). Это очень хорошо тренирует мозг. Поэтому, на мой взгляд, «изобретать велосипед» очень полезно. И категорически вредно всегда пользоваться всем готовым, не имея никакого представления о внутреннем устройстве.
Комментарии (22)

melodictsk
02.10.2019 05:28Может проще открыть учебник по численным методам?
amarao
02.10.2019 11:03+3Мой опыт говорит, что любые хитропопые методы заходят куда лучше, после того, как сам решил задачу ужасающим методом. Вот тогда их хитропопость начинает выглядеть как cleverness. А если начинать с них, то (без понимания масштаба задачи), оно выглядит как "ЗАЧЕМ ЭТО ВСЁ КАКОЙ УЖАС".

Smog1on1the1water
02.10.2019 15:31любые хитропопые методы заходят куда лучше, после того, как сам решил задачу ужасающим методом
Это все абсолютно верно. Но после «сам решил» даже вы не подразумеваете, что на этом нужно останавливаться. А здесь то какой вообще был резон для написания статьи? Ну, решил ты «ужасающим методом», допустим. Проведи тогда хотя бы анализ решения, изучи его сходимость, проверь случая расхождения, поиграйся с оптимизацией, сравни с другими решениями — это все необходимо, чтобы твой опыт действительно стал полезным для других. Но здесь ничего этого и близко нет. Увы, пусть это и мои трудности, но лично я вижу только «не знаю и горжусь этим».
amarao
03.10.2019 14:15Это называется негативный перфекционизм, и с ним лучше бороться.

Smog1on1the1water
03.10.2019 14:28Речь шла как раз об отсутствии здорового желания саморазвиваться (положительного перфекционизма), без которого все превращается, уж прошу извинить меня за мой французский, в «смотрите как красиво я пукнул». Решил сам — молодец, правильный подход, если только это является лишь первым шагом, а не последним.
amarao
03.10.2019 14:33Негативным перфеционизмом является как раз обратное — это когда человеку, который первый раз в жизни что-то сделал приходит кто-то и говорит "ну куда ты со своим рылом в калашный ряд лезешь-то? Вот если бы ты поднапрягся, саморазвился, да показал бы что-то, достойное Старых Мастеров (гигантов, на чьих плечах покоится И. Ньютон), вот тогда да, а так-то ты, куда лезешь-то?".
Негативный перфекнционизм — одна из характерных черт русской культуры, требующей либо восхитить, либо устыдиться.

Smog1on1the1water
03.10.2019 14:41ну куда ты со своим рылом в калашный ряд лезешь-то
Меня удивляет, что вы смогли увидеть такой подтекст в моих словах о том, что: «Решил сам — молодец, правильный подход, если только это является лишь первым шагом, а не последним.»
По факту вы сейчас пытаетесь найти в моей фразе контекст, которого в ней нет, но который беспокоит вас лично.

Refridgerator
02.10.2019 05:45Корень — это слишком просто. Посчитайте, например, гамма-функцию — её как раз и в стандартных библиотеках обычно нет.

Smog1on1the1water
02.10.2019 10:12+4И категорически вредно всегда пользоваться всем готовым, не имея никакого представления о внутреннем устройстве.
Меня несколько смущает следующий вопрос — неужели вы никогда не слышали про итерационную формулу Герона? Было бы весьма похвально додуматься до нее самостоятельно какому-нибудь школьнику или первокурснику, но для профильного выпускника, который прослушал курс лекций по численным методам и вычислительной математике (и, по идее, заведомо перепробовал все эти алгоритмы задолго до окончания обучения), не знать подобных базовых вещей по меньшей мере странно. К сожалению, здесь это выглядит как бравирование собственным незнанием: «Не знаю и знать не хочу».
Логарифмическая сложность алгоритма? Или другая? :)
Алгоритм имеет квадратичную сходимость, как и метод Ньютона, из которого он вытекает.
Кстати, какие возможности ускорения этого алгоритма можно реализовать на ваш взгляд?
Основные правила по поиску возможностей таковы:
1. Подумать самостоятельно (для затравки)
2. Изучить имеющуюся базу/существующие решения
3. Подумать еще раз (о том, как сделать лучше)
4. Верифицировать идею
5. Если результаты неоптимальны, вернуться в пункт 1 и повторить цикл.
У вас здесь, к сожалению, в наличии только шаг 1, шаги 2-5 пропущены, иначе бы вы обнаружили, что одним из известных методов для улучшения выбранного вами метода является прескейлинг. Но лучше все же было бы заведомо исходить из того, что постоянное самообразование является строгой необходимостью для специалиста — меня удивляет, почему нынешняя молодежь не то что книги и учебники не читает, но даже затрудняется прогуляться до гугла и английской википедии, где описано весьма впечатляющее для затравочных размышлений количество методов вычисления корня.

Sirion
02.10.2019 10:19+3Поздравляю, вы изобрели велосипед. Могу понять вашу личную радость открытия, но для прочих учебник по численным методам будет полезнее, потому ценность статьи приблизительно равна нулю.

staticmain
02.10.2019 10:47Дано действительно число a и натуральное число n. Вычислите корень n-ой степени из числа без использование библиотек.
Входные данные: число a — действительное, неотрицательное, не превосходит 1000, задано с точностью до 6 знаков после запятой. Число n — натуральное, не превосходит 10.
Выходные данные: Программа должна вывести единственное число: ответ на задачу с точностью не менее 5 знаков после запятой.
Всего 1000 х 10 = 4000 числе х 8 байт ~ 32 КБ таблиц. Если нужно О(1), можно и предрассчитать.
amarao
02.10.2019 11:176 знаков после запятой забыли. 1000*1000000 — уже миллиард.

staticmain
02.10.2019 11:546 знаков после запятой зашиты в 8 байтах double, раз уж автор в них вычисляет, поэтому 32 КБ.

staticmain
02.10.2019 13:20А, все, понял в чем соль. Да, тогда разве что таблицами с таблицами коррекций.

Pand5461
02.10.2019 10:57+1Как ни странно, почти хорошо.
Радикальное улучшение будет, еслиroot = 0.5 * ( rn + root);заменить наroot = rn / n + root * (1.0 - 1.0 / n);— тогда будет чистый метод Ньютона. Отсюда видно, почему 0.5 для квадратного корня.
По мелочи — 1/rootn можно вычислить за логарифмическое число операций.
И "пять знаков после запятой" чаще интерпретируется как |root/rn — 1| < 10-5, а не как |rootn — rn| < 10-5, иначе для чисел порядка 10-6 будет получаться полная чушь.

Tiriet
03.10.2019 14:08вообще, идея поиска корня довольна простая:
пусть f(x) = x^^n=Y
Err= f(x0)-Y
dErr/dx = n*x^^(n-1)
dx = ( Y-f(x0) )/( n*x^^(n-1) )
x1= x0 + (Y — x0^^n )/(n*x0^^(n-1)) ==>
x1 = x0*(1-1/n) + (1/n)*Y / x0^^(n-1);
собственно, Ваш алгоритм для корня третьей степени отличается от приведенного мной тем, что он «Ваш» (первое) (а мой- Ньютона :-)),
константа 0,5 //root = 0.5 * ( rn + root);// не самая оптимальная в плане сходимости (второе), и вместо деления в цикле лучше использовать умножение, оно считается быстрее, а для корней большой степени его еще и можно ускорить (x^^7 = x*x^^2*(x^^2)^^2, вместо шести умножений- 2 умножения и два(!) возведения в квадрат, для x^^32 ускорение еще приятнее :-)) ( это третье)
double r_n1;
while(mabs(root — rn) >= eps){
r_n1 = 1.0;
for(int i = 1; i < rootDegree; i++){
r_n1 = r_n1 *root;
}
rn = root;
root = rn*(1.0 — 1/rootDegree) + (1.0/rootDegree) *num / r_n1;
countiter++;
}
П.С. а для квадратного корня Вы изобрели формулу Герона. ну как изобрели- Вам ее в школе рассказали, потом Вы ее забыли, а потом- изобрели. «честно нашел».

eversyt
03.10.2019 14:08уже алгоритм для квадратного корня не работает для чисел строго меньше 4. например корень из 2 = 1 :) так как условие root — num / root > eps немного некорректно в этом случае.


mobi
Эх, думал тут будет обзор алгоритмов, а тут даже не Ньютон (и уж тем более не Ньютон для обратного корня).