Наверняка всем доводилось быть свидетелями оценки на глазок степени сходства ребенка с родителями: что-нибудь типа «вылитый папа, но на маму тоже похож!!!»
(взято отсюда)
Как в примере на изображении, можно оценить степень похожести в процентах. Можно задействовать еще родственников, для более точного описания лица малыша в виде взвешенной суммы лиц родни…
И будет это выглядеть и восприниматься вполне естественно для «обычного» человека, не связанного с антропологией, или, например, криминалистикой. Для профессионала в области анализа и распознавания лиц, человеческое лицо представляется, скорее, набором параметров. То есть, точкой (набор координат) в некотором пространстве с базисом (оси, соответствующие параметрам). И если описывать лицо ребенка в сравнении с его родственниками, то скорее всего, точка, соответствующая лицу ребенка окажется в этом пространстве параметров внутри выпуклой оболочки облака точек, соответствующих лицам ближайших родственников (но это не точно).
Собственное, к чему я это все… Эти два подхода к описанию лиц соответствуют двум системам координат:
- барицентрической, описание точки в пространстве (в нашем примере: лица) через взвешенную смесь других точек;
- аффинной, описание точки в пространстве через координаты в некотором базисе.
Так что же такое барицентрические координаты?
Пусть в
-мерном пространстве заданы 
точка 
с радиус-векторами 
, 
. Причем, ни одна из точек не лежит в линейной оболочке радиус-векторов остальных точек… Проще говоря, совсем просто: пусть эти точки образуют фигуру, которую нельзя полноценно представить в пространстве с размерностью меньше .В случае одномерного пространства (линия), нам необходимы 2 не совпадающие точки, случае двумерного пространства — невырожденный треугольник, в случае трехмерного — тетраэдр.
Тогда любая точка пространства
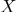может быть представлена радиус-вектором 
:
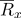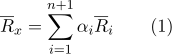
Набор
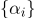и есть барицентрические координаты.Чем барицентрические координаты лучше/хуже аффинных?
Пожалуй, начнем с относительных недостатков:
- в барицентрическом представлении нам необходимо на одну координату больше, чем в аффинном;
- расстояние между точками, заданными барицентрически, нельзя напрямую вычислять в этих координатах.
Отчасти первый недостаток компенсируется тем, что не смотря на необходимость использования
барицентрической координаты при описании точки в -мерном пространстве, количество степеней не повышается. Барицентрические координаты, определенные в формуле (1), связаны соотношением:
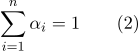
Что касается второго недостатка, если есть необходимость вычисления расстояния между точками, представленными барицентрически, то имеет смысл посчитать скалярные произведения
и использовать аналог расстояния Махаланобиса.Каковы же бонусы от использования барицентрических координат?
- Барицентрические координаты инвариантны к аффинным преобразованиям пространства. Это свойство используется, например, для линейной интерполяции в компьютерной графике. Пусть в вершинах треугольного элемента поверхности определены текстурные координаты
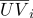и нормали 
(
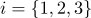), тогда каждая точка этого участка поверхности будет обладать барицентрическими координатами 
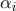, ее текстурные координаты 
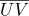и нормаль 
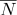могут быть вычислены как:
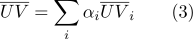
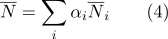
- По барицентрическим координатам легко определить, принадлежит ли точка 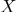части пространства, ограниченной многогранником с вершинами : это выполняется только в том случае, если
. Равенство i-й барицентрической координаты 1 означает, что точка 
совпадает с . Если несколько барицентричесих координат равны 0, то это означает, что точка принадлежит подпространству, натянутому на радиус-вектора остальных точек, соответствующие координаты которых больше 0.
Наверное, они очень сложно вычисляются?
Не сложнее, чем любое линейное преобразование системы координат. Потому что по сути вычисление барицентрических координат таковым преобразованием и является.
Перепишем радиус-вектора точек в следующем виде:
, где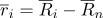 
— радус-вектора в системе координат с центром в точке 
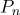.Тогда формулу (1) можно переписать в следующем виде:
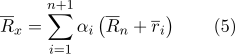
Раскроем скобки в сумме:
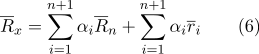
Согласно свойства (2):
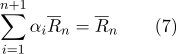
Соответственно:
, где
Учитывая (2), ограничимся вычислением первых n барицентрических координат. Представим переход в барицентрические координаты как линейное преобразование:
,где
— вектор n барицентрических координат (кроме последней), 
— матрица преобразования.Учитывая свойства барицентрического представления, если в качестве
подставить один из векторов 
(
), то мы получим вектор с нулевыми компонентами, кроме одной i-й, которая будет равна 1. Если матрицу
умножить на матрицу 
, составленную по столбцам из , то мы должны получить единичную матрицу (матрицу с единицами на главной диагонали и нулями в остальных элементах):
,где
, 
— единичная матрица (
— символ Кронекера: 1, если 
, иначе — 0).Из (10) находим
:
Таким образом, имея набор из точек с радиус-векторами
, мы можем вычислить матрицу для преобразования в барицентрические координаты:
Используя эту матрицу, мы можем получить первые
барицентрических координат точки с радиус-вектором 
:
Вновь воспользовавшись соотношением (2), получим последнюю барицентрическую координату:
Заключение
Может с первого взгляда барицентрика и кажется неуклюжей и сложной. Но на самом деле, это очень удобный и незаменимый во многих задачах инструмент, к которому довольно быстро привыкаешь. Потому, что тут нет никакой магии, это линейная алгебра в чистом виде!
Комментарии (14)
dmagin
14.10.2019 23:35+2Не люблю критиковать авторов, но все-таки здесь слишком легковесно написано. Пара замечаний для тех, кому важна суть дела:
1. Нет никакого смысла в разделении координат на барицентрические и аффинные. Есть просто разные базисы. Как правило, барицентрическими называют координаты, если базис состоит из одних точек пространства. А если точка всего одна (начало координат), а остальные элементы базиса являются векторами, то типа это привычный аффинный базис. Но могут быть и промежуточные варианты.
Важно лишь, пожалуй, что для определения координат точек пространства в базисе должна быть как минимум одна точка.
2. Из ненужного обособления барицентрических координат следуют их выдуманные недостатки. Нет никаких проблем в определении расстояния между точками. В любых координатах расстояние — это норма вектора. Вектор — это разность точек. Если метрика для базиса задана (скалярные произведения между всеми его элементами), то известны все расстояния в данном базисе.
Ну и т.д.
Пожалуй, ещё надо отметить важное свойство барицентрического базиса — в нем можно оперировать нормой точек, а не только векторов. Это следствие как раз наличия «лишней» координаты.
В целом довольно поверхностная статья, но зато доступна).
mayorovp
15.10.2019 08:47Если бы всё было так же просто — то в разных базисах было бы одинаковое число координат.
dmagin
16.10.2019 09:19Я не уверен, что правильно понял ваше замечание. Если вы вслед за автором намекаете на то, что «барицентрических координат требуется больше», то это неверно.
Для определения координат точки на плоскости достаточно двух любых координат. Так как 3-я всегда может быть определена из условия равенства суммы веса всех координат единице. В векторных координатах данное условие выполняется ввиду наличия начала координат. Это точка и ее вес равен 1. Вес самих векторов нулевой.
Опять же само это условие вытекает из-того, что мы заранее предполагаем, что речь идет именно о координатах точки (для вектора вес координат должен быть равен 0). Если же нужно различать точки и векторы (аффинное пространство), то понадобится еще одна координата. Опять же это требование справедливо для любого базиса.
JamaGava Автор
15.10.2019 09:421) вроде бы писал, что переход в барицентрические координаты, это смена базиса
2) про возможносиь измерения расстояний, если известны произведения радиусов-вектрров точек, — тоже
Но в целом, спасибо за отзыв :)
synedra
15.10.2019 08:02Барицентрические координаты ещё очень удобны для представления в двухмерном рисунке любых трёхэлементных векторов, суммирующихся в единицу. Например (соус):
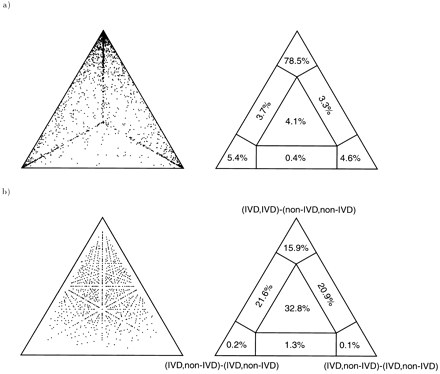
Углы треугольника соответствуют трём взаимоисключающим гипотезам, каждая точка некоторому подмножеству данных, а её координаты — правдоподобия данных под соответствующими гипотезами. Справа посчитано, сколько точек в какой сегмент ложится. Из рисунка сразу видно, как распределяется поддержка между тремя гипотезами.
GeMir
15.10.2019 13:56Давно это было: барицентрические координаты — любимая координатная система моей профессора по линейной алгебре :) Могу ошибаться, но любимым векторным пространством было пространство, образованное многочленами степени меньше n.
vtools
Интересно, есть ли система координат инвариантная к проективное преобразованиям?
Не думали еще об этом? Или в задаче задаче распознавания лиц этого не требуется?
JamaGava Автор
Не знаю, такой системы координат. По крайней мере, среди линейных. А жаль, очень удобно было во многих задачах. И в распознавании лиц тоже.
SunnyA
так основы проективной геометрии
JamaGava Автор
Надо будет порыться в учебниках. Спасибо.
SunnyA
как вариант
Н. И. Мусхелишвили «Курс аналитической геометрии», М.: МГУ, 1967
достаточно доступна
vtools
Это немного не то, нам хочется инвариант к проективным преобразованиям.
evgenyspace
Мне кажется, вы не совсем верно поставили вопрос. Система координат, вообще говоря, не имеет отношения к инвариантам. Тот же вопрос к автору.
Любое преобразование трактуется двояко — как преобразование пространства или же как преобразование системы координат. Инвариант же — это свойство изучаемой формы, сохраняющееся после применении некоторых групп преобразований.
В случае проективного (дробно-линейного) преобразования (а барицентрические координаты являются частным случаем треугольных или однородных, — что одно и тоже) простейшим инвариантом является ангармоническое отношение четырех точек