Пусть в некоторой предметной области исследуются показатели X и Y, которые имеют количественное выражение.
При этом есть все основания полагать, что показатель Y зависит от показателя X. Это положение может быть как научной гипотезой, так и основываться на элементарном здравом смысле. К примеру, возьмем продовольственные магазины.
Обозначим через:
X — торговую площадь(кв. м.)
Y — годовой товарооборот(млн. р.)
Очевидно, что чем выше торговая площадь, тем выше годовой товарооборот(предполагаем линейную зависимость).
Представим, что у нас есть данные о некоторых n магазинах(торговая площадь и годовой товарооборот) — наш датасет и k торговых площадей(X), для которых мы хотим предсказать годовой товарооборот(Y) — наша задача.
Выдвинем гипотезу, что наше значение Y зависит от X в виде: Y = a + b * X
Чтобы решить нашу задачу, мы должны подобрать коэффициенты a и b.
Для начала зададим a и b случайные значения. После этого нам нужно определиться с функцией потерь и оптимизационным алгоритмом.
Для этого мы можем воспользоваться среднеквадратичной функцией потерь(MSELoss). Вычисляется по формуле:
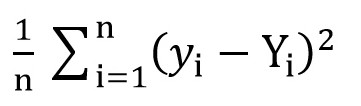
Где y[i] = a + b * x[i] после a = rand() и b = rand(), а Y[i] – правильное значение для x[i].
На данном этапе мы имеем среднеквадратичное отклонение(некую функцию от a и b). И очевидно, что, чем меньше значение этой функции, тем более точно подобраны параметры a и b относительно тех параметров, которые описывают точную зависимость между площадью торгового помещения и товарооборотом в этом помещении.
Теперь мы можем приступить к использованию градиентного спуска(как раз для минимизации функции потерь).
Суть его очень проста. Например, мы имеем функцию:
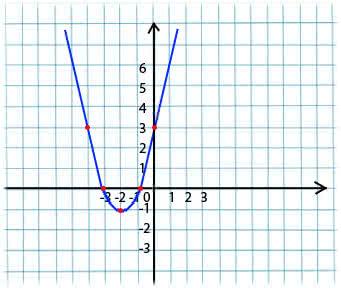
Берем произвольное значение x из области определения функции. Представим, что это точка x1 = -4.
Далее мы берем производную по x от этой функции в точке x1(если функция зависит от нескольких переменных(например, от a и b), то нужно брать частные производные по каждой из переменных). y’(x1) = -4 < 0
Теперь получаем новое значение для x: x2 = x1 – lr * y’(x1). Параметр lr(learning rate) позволяет устанавливать размер шага. Таким образом получаем:
Если частная производная в заданной точке x1 < 0 (функция убывает), то мы движемся к точке локального минимума. (x2 будет больше, чем x1)
Если частная производная в заданной точке x1 > 0 (функция возрастает), то мы все по-прежнему движемся к точке локального минимума. (x2 будет меньше, чем x1)
Выполняя этот алгоритм итерационно, мы приблизимся к минимуму(но не достигнем его).
На практике это все выглядит куда более просто(однако я не берусь утверждать, какие коэффициенты a и b подойдут максимально точно к вышеописанному случаю с магазинами, поэтому возьмем зависимость вида y = 1 + 2 * x для генерации датасета, а потом обучим нашу модель на этом датасете):
(Код написан здесь)
Скомпилировав код, можно заметить, что начальные значения a и b были далеки от требуемых 1 и 2 соответсвенно, а итоговые значения весьма близки.
Немного проясню моменты того, почему у нас a_grad и b_grad считаются именно так.
Материалы, используемые в статье:
towardsdatascience.com/understanding-pytorch-with-an-example-a-step-by-step-tutorial-81fc5f8c4e8e
www.mathprofi.ru/metod_naimenshih_kvadratov.html
При этом есть все основания полагать, что показатель Y зависит от показателя X. Это положение может быть как научной гипотезой, так и основываться на элементарном здравом смысле. К примеру, возьмем продовольственные магазины.
Обозначим через:
X — торговую площадь(кв. м.)
Y — годовой товарооборот(млн. р.)
Очевидно, что чем выше торговая площадь, тем выше годовой товарооборот(предполагаем линейную зависимость).
Представим, что у нас есть данные о некоторых n магазинах(торговая площадь и годовой товарооборот) — наш датасет и k торговых площадей(X), для которых мы хотим предсказать годовой товарооборот(Y) — наша задача.
Выдвинем гипотезу, что наше значение Y зависит от X в виде: Y = a + b * X
Чтобы решить нашу задачу, мы должны подобрать коэффициенты a и b.
Для начала зададим a и b случайные значения. После этого нам нужно определиться с функцией потерь и оптимизационным алгоритмом.
Для этого мы можем воспользоваться среднеквадратичной функцией потерь(MSELoss). Вычисляется по формуле:
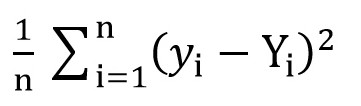
Где y[i] = a + b * x[i] после a = rand() и b = rand(), а Y[i] – правильное значение для x[i].
На данном этапе мы имеем среднеквадратичное отклонение(некую функцию от a и b). И очевидно, что, чем меньше значение этой функции, тем более точно подобраны параметры a и b относительно тех параметров, которые описывают точную зависимость между площадью торгового помещения и товарооборотом в этом помещении.
Теперь мы можем приступить к использованию градиентного спуска(как раз для минимизации функции потерь).
Градиентный спуск
Суть его очень проста. Например, мы имеем функцию:
y = x*x + 4 * x + 3
Берем произвольное значение x из области определения функции. Представим, что это точка x1 = -4.
Далее мы берем производную по x от этой функции в точке x1(если функция зависит от нескольких переменных(например, от a и b), то нужно брать частные производные по каждой из переменных). y’(x1) = -4 < 0
Теперь получаем новое значение для x: x2 = x1 – lr * y’(x1). Параметр lr(learning rate) позволяет устанавливать размер шага. Таким образом получаем:
Если частная производная в заданной точке x1 < 0 (функция убывает), то мы движемся к точке локального минимума. (x2 будет больше, чем x1)
Если частная производная в заданной точке x1 > 0 (функция возрастает), то мы все по-прежнему движемся к точке локального минимума. (x2 будет меньше, чем x1)
Выполняя этот алгоритм итерационно, мы приблизимся к минимуму(но не достигнем его).
На практике это все выглядит куда более просто(однако я не берусь утверждать, какие коэффициенты a и b подойдут максимально точно к вышеописанному случаю с магазинами, поэтому возьмем зависимость вида y = 1 + 2 * x для генерации датасета, а потом обучим нашу модель на этом датасете):
(Код написан здесь)
import numpy as np
# инициализация повторяемой последовательности случайных чисел
np.random.seed(42)
# создаём np-массив из 1000 случайных чисел в диапазоне 0..1
sz = 1000
x = np.random.rand(sz, 1)
# строим функцию y = f(x) и добавляем немного гауссова шума
y = 1 + 2 * x + 0.1 * np.random.randn(sz, 1)
# формируем индексы от 0 до 999
idx = np.arange(sz)
# случайно их тасуем
np.random.shuffle(idx)
train_idx = idx
# формируем наборы обучающих данных
x_train, y_train = x[train_idx], y[train_idx]
# задаём начальные случайные значения коэффициентам линейной регрессии
a = np.random.randn(1)
b = np.random.randn(1)
print(a,b)
# скорость обучения
lr = 0.01
# количество эпох
n_epochs = 10000
# основной цикл
for epoch in range(n_epochs):
# рассчитываем результирующий массив с текущими коэффициентами a и b
# на основе обучающей выборки
yhat = a + b * x_train
# 1. определяем лосс
# считаем отклонение нового результата от обучающего:
error = (y_train - yhat)
# 2. считаем градиенты (вспоминая формулу производной)
# для коэффициента a
a_grad = -2 * error.mean()
# для коэффициента b
b_grad = -2 * (x_train * error).mean()
# 3. обновляем параметры, используя коэффициент скорости обучения
a = a - lr * a_grad
b = b - lr * b_grad
print(a,b)
Скомпилировав код, можно заметить, что начальные значения a и b были далеки от требуемых 1 и 2 соответсвенно, а итоговые значения весьма близки.
Немного проясню моменты того, почему у нас a_grad и b_grad считаются именно так.
F(a, b) = (y_train - yhat) ^ 2 = (1 + 2 * x_train – a + b * x_train). Частная производная F по a будет равняться -2 * (1 + 2 * x_train – a + b * x_train) = -2 * error. Частная производная F по b будет равняться -2 * x_train * (1 + 2 * x_train – a + b * x_train) = -2 * x_train * error. Мы берем среднее значение (mean()) в виду того, что error и x_train, и y_train – это массивы значений, a и b – это скаляры.Материалы, используемые в статье:
towardsdatascience.com/understanding-pytorch-with-an-example-a-step-by-step-tutorial-81fc5f8c4e8e
www.mathprofi.ru/metod_naimenshih_kvadratov.html
Комментарии (11)

ip1981
14.10.2019 20:05+1Скомпилировав код, можно заметить...
… что текст и код писали разные люди? :)

Sly_tom_cat
15.10.2019 11:57Тоже резануло глаз:
Сочетание питоновского кода и слов «Скомпилировав код» вызвали глубокий когнитивный диссонанс.


Dark_Daiver
Никогда не понимал, ради чего. Это же выпуклая задача, не важно откуда мы стартуем, а работать с 0 в качестве инициализации проще
Ну и да, при наличии аналитического решения использовать GD как-то наивно
CrazyElf
В данном случае функция выпуклая, но в общем случае у функции могло бы быть несколько локальных минимумов, поэтому в начале обычно и берут рандомы, чтобы не проваливаться стабильно в один и тот же локальный минимум, начиная с одних и тех же начальных условий.
А shuffle думаю тут нужен был на случай разбиения данных на train и test, которого в данном коде и нет %)
Dark_Daiver
Думается мне, что это был типа задел на еще одну статью про обучение нейронок. Тогда shuffle это для минибатчей, а случайная инициализация для того, чтобы сломать симметрию градиентов.
Прощупывать минимумы при помощи рандома конечно можно, но делают так редко ибо нет особых гарантий. Для мл, как мне кажется, проблема плохого минимума при обучении не особо стоит. Другое дело, что модели с разной инициализацией можно использовать для ансамблей.
sinc
Вот лепят нейронки куда не попадя. В нейчур была недавно статья про предсказание землетрясений. Там использовалась очень глубокая сеть. Но как оказалось достаточно лишь двух параметров, чтобы достичь той же точности предсказания. А тремя параметрами можно даже лучше.
akhkmed
При этом аналитическое решение требует всего O(1) дополнительной памяти и O(N) вычислений.