Для ответа на вопрос в заголовке - погрузимся в статью.
Статья уже была частично разобрана в статье на Хабре, я же хочу погрузиться в статью более глубоко. Ближе к концу статьи начнет появляться не совсем тривиальная математика - ее можно усваивать поверхностно :)
Больше разборов статей можно найти у меня в блоге - в основном обозреваю статьи по теме Face Anti-Spoofing'а, но бывают и другие.
Саммари статьи
Обычно LLM-ку предобучают на огромном корпусе, потом адаптируют на down-stream tasks. Если LLM-ка была большая, то мы не всегда можем в full fine-tuning. Авторы статьи предлагают Low-Rank Adaptation (LoRA), который замораживает предобученные веса модели и встраивает "rank decomposition matrices" в каждый слой трансформера, очень сильно понижая кол-во обучаемых параметров для downstream tasks.
Compared to GPT-3 175B fine-tuned with Adam, LoRA can reduce the number of trainable parameters by 10,000 times and the GPU memory requirement by 3 times. LoRA performs on-par or better than finetuning in model quality on RoBERTa, DeBERTa, GPT-2, and GPT-3, despite having fewer trainable parameters, a higher training throughput, and, unlike adapters, no additional inference latency.
Многие NLP-приложения требуют решения разных задач, что зачастую достигается путем дообучения большой модели на несколько разных downstream tasks. Самая важная проблема в классическом fine-tuning'е - новая модель содержит столько же параметров, сколько начальная.
Есть работы, где авторы адаптируют только некоторые параметры или обучают внешний модуль для каждой новой задачи. Таким образом, нам необходимо для каждой новой задачи хранить лишь веса, связанные с этой задачей. Однако, имеющиеся методы страдают от:
Inference latency (paper 1 - Parameter-Efficient Transfer Learning for NLP)
Reduced model's usable sequence length (paper 2 - Prefix-Tuning: Optimizing Continuous Prompts for Generation)
Часто не достигают бейзлайнов, если сравнивать с "классическим" fine-tuning'ом
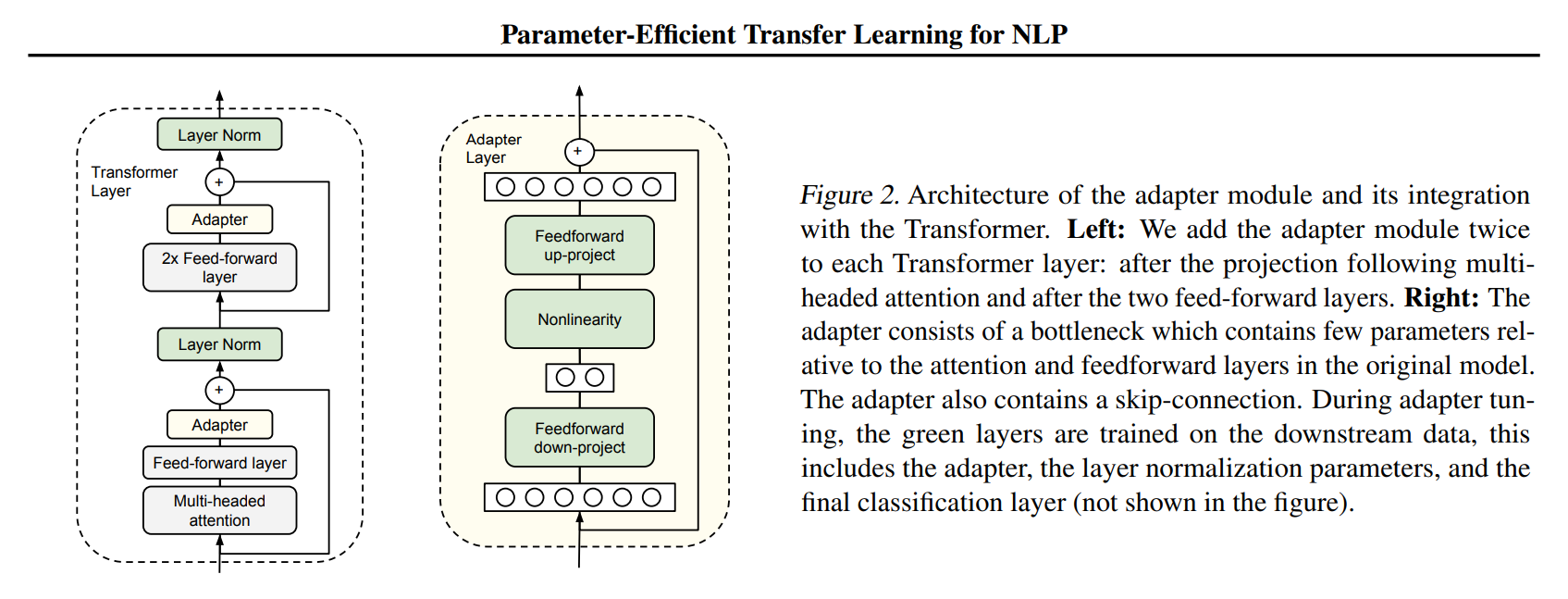
На картинке выше из статьи виден пример добавления адаптеров в слои трансформера. Такой адаптер назвали в статье AdapterH (в замерах inference latency, см. ниже Table 1). Появились новые слои - их не смерджить со старыми слоями, в том числе полносвязными ==> получаем небольшое замедление инференса.
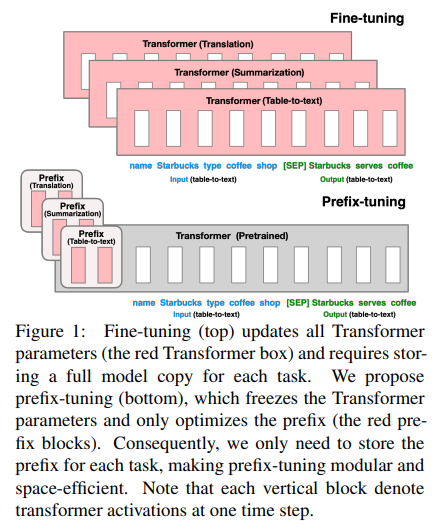
В этой статье (см. картинку выше) авторы предложили в качесве Parameter-Efficient Fine-Tuning (PEFT) часть начальных эмбеддингов заразервировать под задачу. Работает это следующим образом:

Получаем h_i совершенно обычным (авторегрессионным) образом, но с одним изменением:

Получается, что начальные состояния берутся просто из матрицы с эмбеддингами, которые в процессе обучения изменяются. На инференсе же для каждой задачи соответствует своя матрица. В таком подходе мы уменьшаем длину последовательности, которую модель может скушать во время инференса (аналогично добавлению промпта в модель).

Авторы LoRA вдохновлялись двумя статьями: 1) paper 3 - MEASURING THE INTRINSIC DIMENSION OF OBJECTIVE LANDSCAPES; 2) paper 4 - INTRINSIC DIMENSIONALITY EXPLAINS THE EFFECTIVENESS OF LANGUAGE MODEL FINE-TUNING
paper 3 (TL;DR - кол-во параметров в моделях обычно избыточно, давайте поисследуем этот момент):
In this paper we attempt to answer this question by training networks not in their native parameter space, but instead in a smaller, randomly oriented subspace. We slowly increase the dimension of this subspace, note at which dimension solutions first appear, and define this to be the intrinsic dimension of the objective landscape.
paper 4 (TL;DR - поисследуем избыточность в LLM-ках):
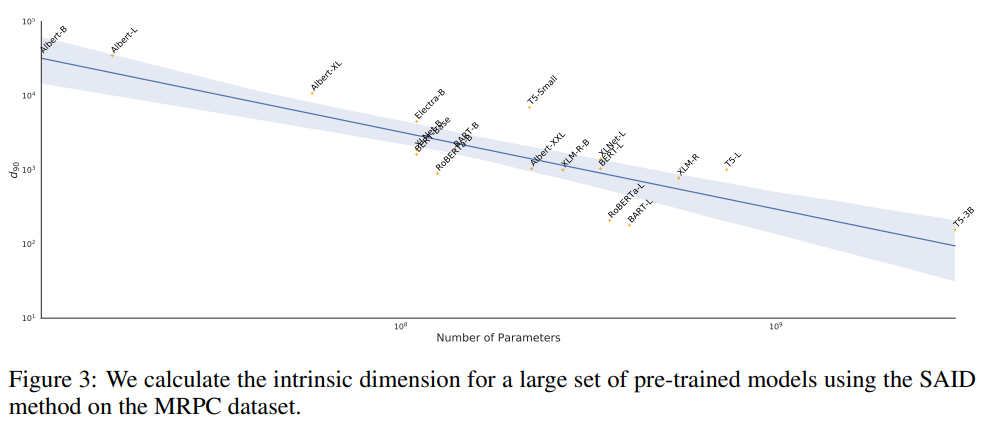
Поисследовали, получилось, что чем больше кол-во параметров, тем ниже intrinsic dimension.
В главе 6 можно прочесть дополнительно о предыдущих работах в направлении, связанном с PEFT.
Что предлагают авторы LoRA:
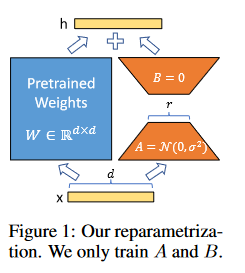
За каждую задачу отвечают A и B. Для новой задачи - меняем A и B (меньше занимаем места, если сравнивать с обычным fine-tuning'ом)
Легко и быстро обучается (за счет маленьких размеров (low-rank) A и B - об этом дальше)
A и B можно смержить с предобученными весами во время деплоя (1. W; 2. W + B@A)
LoRA ортогональна (независима) относительно многих других методов Parameter-Efficient Fine-Tuning ==> можно комбинировать (см. в статье авторов Appendix E)
Перед началом обучения A семплируется из нормального распределения, B просто нулевая матрица. Далее обучается это все с местным lr, который равен alpha/r.
When optimizing with Adam, tuning α is roughly the same as tuning the learning rate if we scale the initialization appropriately.
Изложенные авторами принципы применимы к любым полносвязным слоям в моделях глубокого обучения, хотя в своих экспериментах они фокусируются только на определенных весах трансформера.
∆W = BA совпадает по размерам с W, аутпут слоя считается следующим образом:
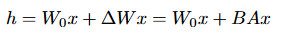
A Generalization of Full Fine-tuning
Такой подход, грубо говоря, сходится к дообучению оригинальной модели, тогда как adapter-based методы сходятся к MLP, а prefix-based методы к моделям, которые не могут принимать на вход слишком длинные последовательности.
A more general form of fine-tuning allows the training of a subset of the pre-trained parameters. LoRA takes a step further and does not require the accumulated gradient update to weight matrices to have full-rank during adaptation. This means that when applying LoRA to all weight matrices and training all biases, we roughly recover the expressiveness of full fine-tuning by setting the LoRA rank r to the rank of the pre-trained weight matrices. In other words, as we increase the number of trainable parameters, training LoRA roughly converges to training the original model, while adapter-based methods converges to an MLP and prefix-based methods to a model that cannot take long input sequences.
No Additional Inference Latency
W = W_0 + BA; далее инференсим как обычную модель
Авторы ограничивают исследование только адаптацией весов внимания для и замораживают модули MLP для простоты. Как ведет себя адаптация для MLP, LayerNorm и смещений - авторы оставляют на future work.
WHICH WEIGHT MATRICES IN TRANSFORMER SHOULD WE APPLY LORA TO?
Given a limited parameter budget, which types of weights should we adapt with LoRA to obtain the best performance on downstream tasks? As mentioned in Section 4.2, we only consider weight matrices in the self-attention module. We set a parameter budget of 18M (roughly 35MB if stored in FP16) on GPT-3 175B, which corresponds to r = 8 if we adapt one type of attention weights or r = 4 if we adapt two types, for all 96 layers. The result is presented in Table 5.

Лучше адаптировать бОльшее кол-во типов матриц с меньшим (соответственно, сохраняя parameter budget) рангом.
WHAT IS THE OPTIMAL RANK r FOR LORA?

Достаточно низкие ранги достаточны, но авторы предупреждают:
However, we do not expect a small r to work for every task or dataset. Consider the following thought experiment: if the downstream task were in a different language than the one used for pre-training, retraining the entire model (similar to LoRA with r = dmodel) could certainly outperform LoRA with a small r.
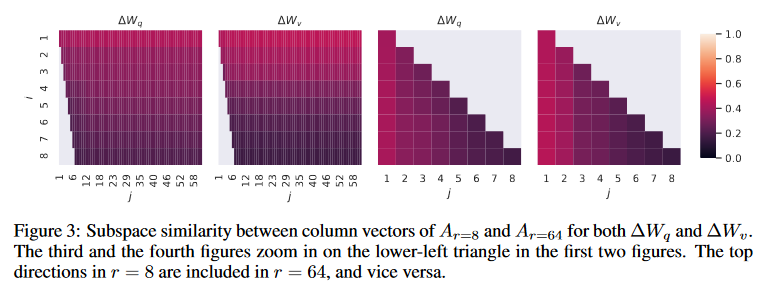
Взяли A_r=8 и A_r=64, сделали SVD разложение, посмотрели на сингулярные вектора с помощью Grassmann distance:

φ(·) имеет диапазон [0, 1], где 1 представляет полное перекрытие подпространств, а 0 — полное разделение.
Directions corresponding to the top singular vector overlap significantly between Ar=8 and Ar=64, while others do not. Specifically, ∆Wv (resp. ∆Wq) of Ar=8 and ∆Wv (resp. ∆Wq) of Ar=64 share a subspace of dimension 1 with normalized similarity > 0.5, providing an explanation of why r = 1 performs quite well in our downstream tasks for GPT-3.
Верхние сингулярные вектора (соответствующие наибольшим сингулярным значениям) самые важные, они и выучиваются - проще говоря. Отсюда, на мой взгляд, можно отталкиваться при тюне параметра r для какой-то конкретной задачи :) Подробнее про Grassmann distance в Appendix G статьи.

Даже через разные сиды получается аналогичная картинка. По ней, кстати говоря, видно, что у Wq intrinsic rank выше, чем у Wv.
Авторы обещают, что точно такой же анализ можно проделать с матрицей B. Чтож, верим :)
HOW DOES THE ADAPTATION MATRIX ∆W COMPARE TO W?
Коррелируют ли эти две матрицы? (Более формально, состоит ли ∆W в основном из верхних сингулярных направлений W?)
Для ответа на вопрос W проецируют на подпространство размера r, задаваемое сингулярными векторами матрицы ∆W. (U - левые сингулярные вектора, V - правые). Сингулярные вектора считают как на матрице ∆W, так и на матрицах W и на рандомной матрице. Потом сравнивают между собой нормы Фробениуса для 1. U^TWV^T; 2. W.

U^TWV^T (где U и V были посчитаны на W) скорее всего стремится к 61.95. Здесь чуть-чуть черипикнуто, как по мне (каким образом рандом выбирался (какое распределение)? Что для остальных r?). Идея конечно в том, чтобы сравненить нормы Фробениуса для матриц U^TWV^T и W ==> оценить, насколько сильно матрица W отличается от своей проекции на подпространство, описываемое матрицей A, матрицей W (самой же себя) и рандомной матрицей (вернее их сингулярными векторами). Далее авторы утверждают:
First, ∆W has a stronger correlation with W compared to a random matrix, indicating that ∆W amplifies some features that are already in W . Second, instead of repeating the top singular directions of W , ∆W only amplifies directions that are not emphasized in W . Third, the amplification factor is rather huge: 21.5 ≈ 6.91/0.32 for r = 4. See Section H.4 for why r = 64 has a smaller amplification factor. We also provide a visualization in Section H.3 for how the correlation changes as we include more top singular directions from Wq. This suggests that the low-rank adaptation matrix potentially amplifies the important features for specific downstream tasks that were learned but not emphasized in the general pre-training model.
Во-первых, корреляция лучше чем со случайной матрицей - окей :) Но вывод интересный они делают - ∆W усиливает некоторые признаки, которые уже есть в W. И, во-вторых, вместо повторения верхний сингулярных векторов W, ∆W усиливает те, которые "не подчеркнуты" внутри W. В-третьих, это усиление равно примерно 21.5=6.91/0.32 для r=4. В секции H.4 рассказано про то, почему при r=64 это не проявляется так явно:
This should not be surprising, and in fact gives evidence (once again) that the intrinsic rank needed to represent the “task-specific directions” (thus for model adaptation) is low.
Больше ничего про это не пишут. Лично мне не совсем понятна связь малого количества “task-specific directions” и низкого отношения норм Фробениуса для r=64, но это в целом не суть - идея "Second, instead of repeating the top singular directions of W , ∆W only amplifies directions that are not emphasized in W" мне нравится куда больше :)
Еще парочка табличек и закончим.
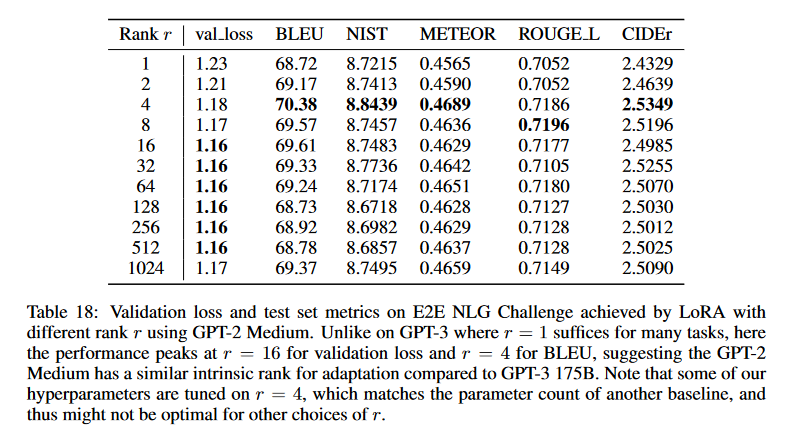
Такой рисеч надо делать самому скорее всего, потому что:
Note that some of our hyperparameters are tuned on r = 4, which matches the parameter count of another baseline, and thus might not be optimal for other choices of r.
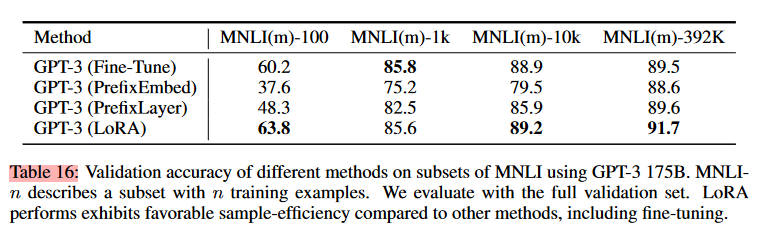




Adpt_H (paper 1) выше, LoRA - понятно, BitFit - учим только смещения, FT - fine-tune (full, на сколько я понял), FT_top2 - fine-tune верхних двух слоев, PreEmbed - выше (paper 2), PreLayer - вместо новых матриц в инпуте (как у PreEmbed) учим активации между слоями (очень похоже на paper 1).
Заключение
There are many directions for future works. 1) LoRA can be combined with other efficient adaptation methods, potentially providing orthogonal improvement. 2) The mechanism behind fine-tuning or LoRA is far from clear – how are features learned during pre-training transformed to do well on downstream tasks? We believe that LoRA makes it more tractable to answer this than full finetuning. 3) We mostly depend on heuristics to select the weight matrices to apply LoRA to. Are there more principled ways to do it? 4) Finally, the rank-deficiency of ∆W suggests that W could be rank-deficient as well, which can also be a source of inspiration for future works.
Особенно 4й пункт мне нравится :)
P.S. pdf с небольшими комментариями и хайлайтами статьи можно найти в у меня в блоге

