В 2000 году профессор Пармского университета Анджело Фарина предложил оригинальный метод одновременного измерения импульсной характеристики и нелинейных искажений с помощью гармонического сигнала экспоненциально изменяющейся частоты (далее ESS – exponential sine sweep).
Для получения этих характеристик необходимо записать воздействие ESS-сигнала на испытуемое устройство и найти взаимную корреляционную функцию записанного сигнала с исходным ESS-сигналом, но промодулированным по амплитуде (подробнее об этом можно узнать в публикациях А.Фарина).
В результате получается набор импульсных характеристик (ИХ), последняя из которых является линейной импульсной характеристикой устройства. Ей предшествует импульсная характеристика квадратичной нелинейности устройства, перед ней – импульсная характеристика кубической нелинейности и т.д. На практике удаётся зафиксировать нелинейности до 20 порядка.
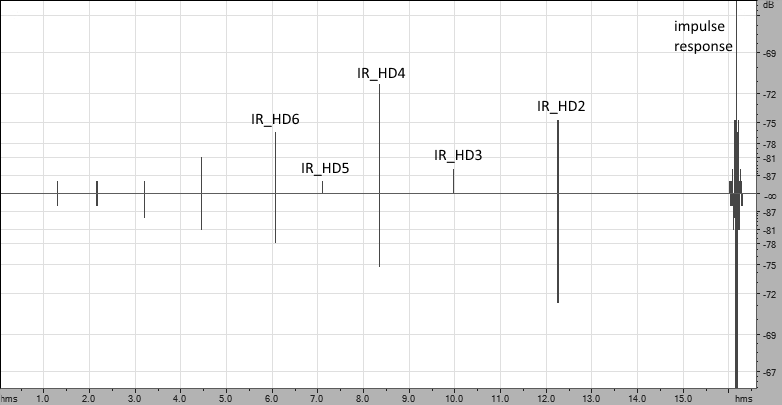
Эта особенность (отделение продуктов нелинейности от линейной импульсной характеристики) является уникальным преимуществом ESS-метода по сравнению с другими методами. ESS-метод обладает и другими преимуществами:
Расположение характеристик искажений относительно линейной импульсной характеристики можно найти по следующему правилу: если частота ESS-сигнала растёт со скоростью 1 октава в секунду, то характеристика нелинейности 2-го порядка будет расположена за 1 секунду до линейной импульсной характеристики; характеристика нелинейности 4-го порядка будет расположена за 1 секунду до характеристики 2-го порядка и т.д.
Несмотря на очевидные преимущества, ESS-метод имеет и свои границы применения. Сам автор метода перечисляет следующие ограничения:
Для снижения неравномерности АЧХ и импульсной характеристики А.Фарина предлагает модулировать начало ESS-сигнала по амплитуде (fade-in), а также применять различные техники фильтрации.
Другой энтузиаст, Katja Vetter в своём исследовании обнаружил другую проблему, связанную с тем, что каждая октава сигнала начинаются не в нулевой фазе. Это накладывает погрешность на измерение гармоник. В качестве решения автор предложил новый подход к формированию ESS-сигнала: каждая октава должна начинаться с нулевой фазы.
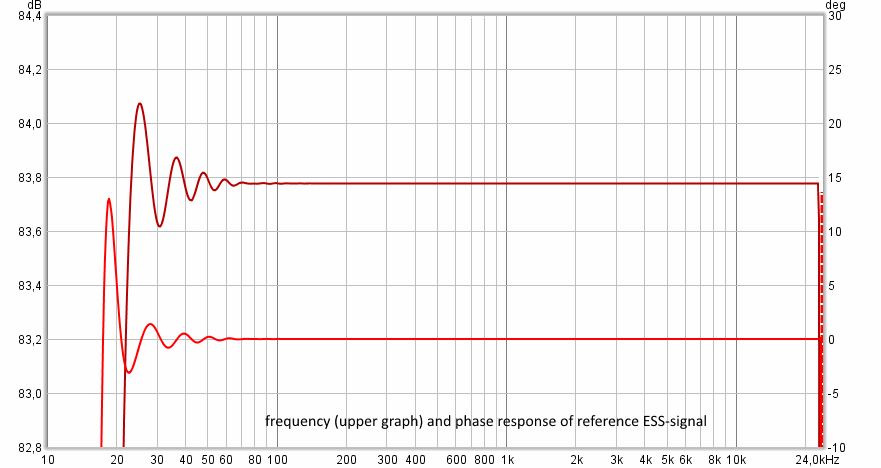
Путём подбора и моделирования в MATLAB был сгенерирован ESS-сигнал длительностью в 43 секунды, диапазоном в 11 октав (11.7-24000Гц), с амплитудным модулированием краёв сигнала. Это позволило получить неравномерность АЧХ <0.2дБ на краях диапазона измерения (22 и 23000 Гц) и уровень относительной погрешности <-140дБ.
ESS-метод оказался очень полезным при наладке эквалайзера, собранного на операционных усилителях. Схема проявляла неустойчивость, причину которой сложно было проанализировать. ESS-методом удалось определить, что устройство имело повышенные нелинейные искажения в области частот работы эквалайзера.

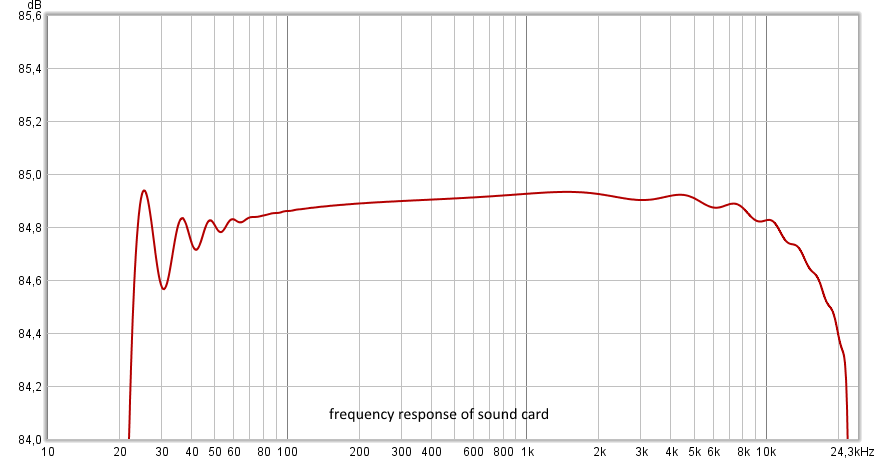
В данном примере выход аудиокарты был соединён со входом и производилось измерение сквозной АЧХ устройства. Как видно, некоторая неравномерность (в регионе 20-60Гц) связана с погрешность самого ESS-метода. Остальной же вклад в неравномерность относится к аудиокарте.
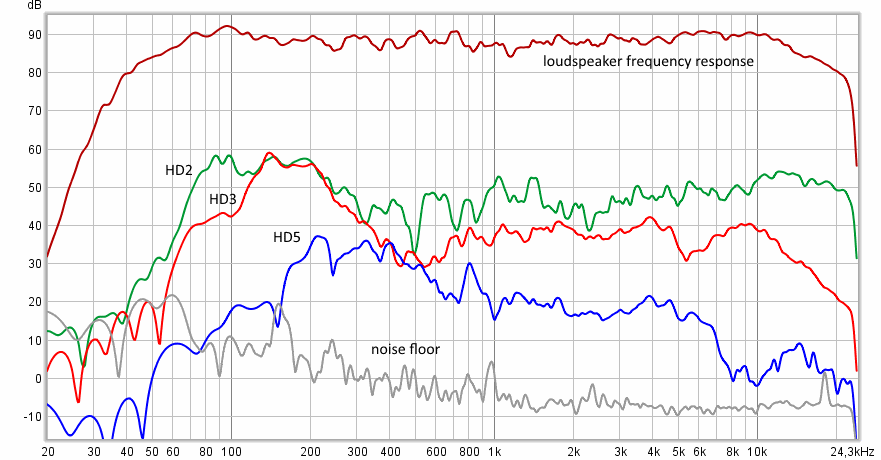
В данном примере приведены измерения АЧХ студийных мониторов в ближнем поле. В данном случае отношение сигнал/шум составило 90дБ, при этом измерения производились в студийном помещении при умеренном уровне звукового давления (не более 90дБ SPL).
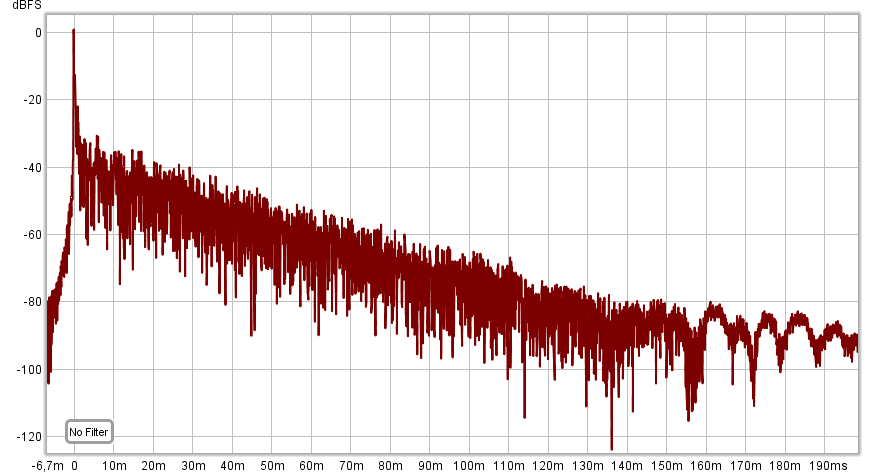
Огибающая измеренной импульсной характеристики студийного монитора (видно, что динамический диапазон измерения составил 90дБ).
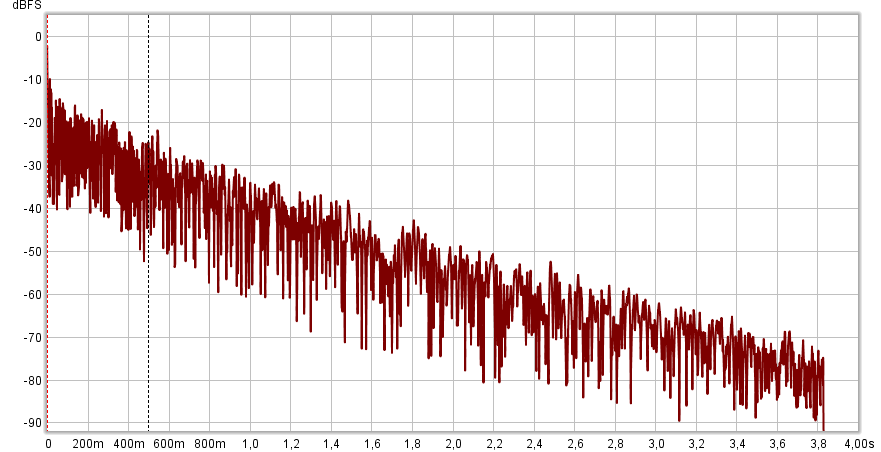
В этом примере представлена огибающая импульсной характеристики отклика помещения. Время реверберации составило 3.8 секунд. Как видно, энергия затухает равномерно и без всплесков вплоть до самых низких уровней.
Метод, предложенный А.Фарина, позволяет проводить высокоточные измерения электронных и электроакустических устройств, а также акустических свойств помещений. Известно, что этот метод успешно применяется в программах акустический измерений, таких как CLIO и REW.
Полезные ссылки:
Для получения этих характеристик необходимо записать воздействие ESS-сигнала на испытуемое устройство и найти взаимную корреляционную функцию записанного сигнала с исходным ESS-сигналом, но промодулированным по амплитуде (подробнее об этом можно узнать в публикациях А.Фарина).
В результате получается набор импульсных характеристик (ИХ), последняя из которых является линейной импульсной характеристикой устройства. Ей предшествует импульсная характеристика квадратичной нелинейности устройства, перед ней – импульсная характеристика кубической нелинейности и т.д. На практике удаётся зафиксировать нелинейности до 20 порядка.

Эта особенность (отделение продуктов нелинейности от линейной импульсной характеристики) является уникальным преимуществом ESS-метода по сравнению с другими методами. ESS-метод обладает и другими преимуществами:
- Повышенная устойчивость к случайному шуму. Так получается потому, что гармонический сигнал «сканирует» очень узкий частотный промежуток в каждый интервал времени, что позволяет уменьшить уровень случайного шума в результирующей импульсной характеристике. Чем продолжительнее ESS-сигнал — тем заметнее эффект снижения уровня шума.
- Простота использования. Вся процедура декодирования сводится к нескольким вычислениям методом БПФ.
- Возможность автоматизации процесса измерений.
Расположение характеристик искажений относительно линейной импульсной характеристики можно найти по следующему правилу: если частота ESS-сигнала растёт со скоростью 1 октава в секунду, то характеристика нелинейности 2-го порядка будет расположена за 1 секунду до линейной импульсной характеристики; характеристика нелинейности 4-го порядка будет расположена за 1 секунду до характеристики 2-го порядка и т.д.
Несмотря на очевидные преимущества, ESS-метод имеет и свои границы применения. Сам автор метода перечисляет следующие ограничения:
- Результирующая импульсная характеристика, а также её АЧХ имеет заметную неравномерность («звон»)
- Метод чувствителен к нестабильности временной оси
Для снижения неравномерности АЧХ и импульсной характеристики А.Фарина предлагает модулировать начало ESS-сигнала по амплитуде (fade-in), а также применять различные техники фильтрации.
Другой энтузиаст, Katja Vetter в своём исследовании обнаружил другую проблему, связанную с тем, что каждая октава сигнала начинаются не в нулевой фазе. Это накладывает погрешность на измерение гармоник. В качестве решения автор предложил новый подход к формированию ESS-сигнала: каждая октава должна начинаться с нулевой фазы.
Практические примеры применения ESS-метода.
Путём подбора и моделирования в MATLAB был сгенерирован ESS-сигнал длительностью в 43 секунды, диапазоном в 11 октав (11.7-24000Гц), с амплитудным модулированием краёв сигнала. Это позволило получить неравномерность АЧХ <0.2дБ на краях диапазона измерения (22 и 23000 Гц) и уровень относительной погрешности <-140дБ.

Измерение характеристик ячейки эквалайзера (частотного корректора).
ESS-метод оказался очень полезным при наладке эквалайзера, собранного на операционных усилителях. Схема проявляла неустойчивость, причину которой сложно было проанализировать. ESS-методом удалось определить, что устройство имело повышенные нелинейные искажения в области частот работы эквалайзера.

Измерение характеристик компьютерной аудиокарты.
В данном примере выход аудиокарты был соединён со входом и производилось измерение сквозной АЧХ устройства. Как видно, некоторая неравномерность (в регионе 20-60Гц) связана с погрешность самого ESS-метода. Остальной же вклад в неравномерность относится к аудиокарте.

Измерение акустических характеристик громкоговорителя
В данном примере приведены измерения АЧХ студийных мониторов в ближнем поле. В данном случае отношение сигнал/шум составило 90дБ, при этом измерения производились в студийном помещении при умеренном уровне звукового давления (не более 90дБ SPL).


Огибающая измеренной импульсной характеристики студийного монитора (видно, что динамический диапазон измерения составил 90дБ).
Измерение акустических характеристик помещения
В этом примере представлена огибающая импульсной характеристики отклика помещения. Время реверберации составило 3.8 секунд. Как видно, энергия затухает равномерно и без всплесков вплоть до самых низких уровней.

Метод, предложенный А.Фарина, позволяет проводить высокоточные измерения электронных и электроакустических устройств, а также акустических свойств помещений. Известно, что этот метод успешно применяется в программах акустический измерений, таких как CLIO и REW.
Полезные ссылки:
- Simultaneous measurement of impulse response and distortion with a swept-sine technique
- Advancements in impulse response measurements by sine sweeps
- Impulse response measurement with sine sweeps and amplitude modulation schemes
- Optimizing the exponential sine sweep (ESS) signal for in situ measurements on noise barriers
Комментарии (6)

Refridgerator
17.10.2019 06:40Было бы интереснее, если бы вы на одних и тех же данных сравнили результаты по методу Фарины с классическими способами — измерение только АЧХ импульсом/свиптоном и гармоник на отдельно взятых частотах.

VladimirGodyna Автор
17.10.2019 21:57В первой ссылке (в конце статьи) на 24 странице, рис.20 приводится очень хорошее сравнение по нелинейным искажениям. Там же есть сравнение ESS с MLS методов.


Gryphon88
Извините, мне кажется, или тут много общего с гетеродинированием?
VladimirGodyna Автор
Всё-таки, гетеродинирование — это нелинейное преобразование. Но стратегия чем-то похожа.
lz961
Да, интересно было бы сопоставить предложенный метод с чирплетами (вейвлет, базовая функция которого — радиоимпульс с линейной частотной модуляцией) с одной стороны, и методами, применяемыми в современных анализаторах АЧХ/ФЧХ.
VladimirGodyna Автор
Добавил в конце статьи несколько ссылок, посвящённых исследованию этого алгоритма. В 3-й ссылке есть сравнение экспоненциального и линейного свипа. Если срезюмировать: экспоненциальный свип отделяет продукты нелинейности в отдельные импульсные характеристики. Линейный свип не имеет такого преимущества. В плане соотношения сигнал/шум линейный и экспоненциальный свип отличаются распределением по спектру, но одинаковы по энергии.