В тексте везде идет речь про обучение с учителем. Набор данных для обучения модели называется тренировочный сет. Независимые переменные носят названия фичи, зависимую я называю целевой переменной. Я предполагаю, что эти слова читателю знакомы.
Отбор фич (feature selection)
Почему отбор фич вообще необходим. Основных причин две. Во-первых, если фич очень много, то увеличивается время работы классификатора. Если стоит цель протестировать несколько классификаторов с целью выбора лучшего, то время необходимое на вычисления может стать просто огромным. Кроме того, данные (тренировочный сет) могут перестать помещаться в оперативную память, тогда придется модифицировать алгоритмы классификаторов. Может перестать помещаться даже одна строка сета, хотя это уже редкий случай.
Главная причина все-таки вторая — с увеличением количества фич часто падает точность предсказания. Особенно если в данных много мусорных фич (мало коррелирующих с целевой переменной). Это явление называется переобучение (overfitting).
Методы отбора фич делятся на три категории: filter methods, wrapper methods и embedded methods. Первую категорию я буду назвать “методы фильтрации”, последнюю — “встроенные методы”, а для второй у меня нет адекватного перевода (выслушаю предложения).
Методы фильтрации (filter methods)
Они основаны на статистических методах и, как правило, рассматривают каждую фичу независимо. Позволяют оценить и ранжировать фичи по значимости, за которую принимается степень корреляции этой фичи с целевой переменной. Рассмотрим несколько примеров.
Informaition gain
Один из примеров методов фильтрации фич (filter methods) — informaition gain. Он тесно связан с понятием энтропии информации. Формулой энтропия выражается довольно просто:
Где, p(xi) — вероятность того, что переменная X примет значение xi. В наших условиях эта вероятность считается как количество записей (примеров), в которых X=xi, разделенное на общее количество записей.
Чтобы лучше понять смысл этой меры, можно представить два простых примера. Во-первых, подбрасывание монетки, у которой выпадение орла и решки равновероятны. В этом случае энтропия, рассчитанная по формуле, будет равна 1. Если же монета всегда падает исключительно орлом вверх, то энтропия будет равна 0. Иными словами высокая энтропия говорит о равномерном распределении, низкая — о каком-то более интересном.
Для расчета корреляции между переменными нам понадобится определить еще несколько мер. Первая из них — specific conditional entropy:
Относительная энтропия (conditional entropy) считается как:
Интересная такая величина не сама по себе, а ее разница с обычной энтропией фичи Y. Т.е. как бы мера того, насколько более упорядоченной становится для нас переменная Y, если мы знаем значения X. Или, говоря проще, существует ли корреляция между значениями X и Y, и насколько она велика. Об этом говорит величина information gain:
Чем больше параметр IG — тем сильнее корреляция. Таким образом, мы легко можем вычислить information gain для всех фич и выкинуть те, которые слабо влияют на целевую переменную. Тем самым, во-первых, сократив время расчета модели, а, во-вторых, уменьшив опасность переобучения.
Хи-квадрат (chi-square)
Рассмотрим еще один популярный метод фильтрации фич, называемый chi-square test. Для того чтобы в нем разобраться понадобится вспомнить пару формул из теории вероятности. Первая из них это формула для вероятности пересечения (умножения) событий. Т.е. вероятность того, что произойдут оба события A и B:
Где P(A/B) — вероятность того, что произойдет событие A, если B уже наступило. Если эти события независимы (наступление одного из них никак не влияет на вероятность наступления другого), то:
Исходя из этой формулы, можно посчитать ожидаемую вероятность наступления одновременно событий A и B, если мы предполагаем, что они независимы. А затем вычислить, насколько реальность отличается от наших ожиданий. Формула хи-квадрат выглядит так:
Рассмотрим ее использование на примере. Предположим, мы хотим исследовать влияние некого воздействия на возникновение определенной болезни. Таблица с имеющейся у нас статистикой выглядит так:
| Болезнь | |||
| Воздействие | Есть | Нет | Всего |
| Было | 37 | 13 | 50 |
| Не было | 17 | 53 | 70 |
| Всего | 54 | 66 | 120 |
Где ячейка на пересечении первой строки и первого столбца отражает количество подвергшихся воздействию и заболевших; первой строки и второго столбца — количество подвергшихся воздействию, но не заболевших и т.д.
Рассчитаем ожидаемое значение для первой ячейки (те, кто подвергся воздействию и заболел):
Аналогично для других ячеек. И по формуле вычисляем хи-квадрат (в данном случае он равен 29.1).
Таким образом, для независимых событий параметр хи-квадрат будет равен нулю (или числу близкому к нему). Но чтобы точно понять, какова вероятность получить такую картину для двух независимых событий, вводят еще одно понятие — степень свободы. Она определяется как:
(#значения_переменной1 — 1)*(#значения_переменной_2 — 1)
Где #значения_переменной1 — количество значений, которые может принимать переменная 1 (для нашего случая степень свободы = 1).
Для того чтобы имея значение хи-квадрат и степень свободы можно было прикинуть вероятность существуют специальные таблицы (типа этой(https://www.easycalculation.com/statistics/chisquare-table.php)).
Некоторое представление о работе алгоритма мы получили. Но разумеется в реальности не будет необходимости ни писать этот алгоритм самостоятельно, ни тем более считать статистику вручную. Библиотека scikit-learn для питона дает возможность не задумываться о деталях реализации:
from nltk import WordNetLemmatizer
from sklearn.feature_selection import chi2
from sklearn.feature_selection import SelectKBest
select = SelectKBest(chi2, k=50)
X_new = select.fit_transform(train_data_features, train["sentiment"])
В моей прошлой статье как раз можно найти пример эффективности применения хи-квадрат статистики для решения NLP задачи.
mRmR
Отдельно хочу кратко остановиться на более сложном методе фильтрации, который учитывает не только корреляцию между фичами и целевой переменной, но так же избыточность фич — mRmR (минимальная избыточность при максимальной релевантности). Метод пытается максимизировать следующее выражение:
Где первое слагаемое отвечает за максимизацию корреляции между выбранным набором фич S и целевой переменной Y (аналогично методу informaition gain), а второе за минимизацию корреляций между фичами. Таким образом полученный набор фич не только релевантен, но и фичи в этом наборе минимально повторяют друг друга. В этом методе фичи в набор добавляются по одной с выбором оптимальной на каждом шаге.
Плюсы и минусы методов фильтрации
Чем этот класс методов хорош? У них низкая стоимость вычислений, которая зависит линейно от общего количества фич. Они значительно быстрее и wrapper и embedded методов. К тому же они хорошо работают даже тогда, когда число фич у нас превышает количество примеров в тренировочном сете (чем далеко не всегда могут похвастаться методы других категорий).
В чем их недостатки? Они рассматривают каждую фичу изолированно. Из-за этого найти топ-N наиболее коррелирующих фич вообще говоря не означает получить подмножество, на котором точность предсказания будет наивысшей. Рассмотрим простой пример.
Предположим, что есть некий массив фич, среди которых X1 и X2. Целевая переменная зависит от них как:
(логическая функция XOR)
Таблица истинности будет выглядеть так (если кто забыл):
| X1 | X2 | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Глядя на эту таблицу, построим таблицу со статистикой для переменной X1 и вычислим ее корреляцию с переменной Y (для X2 будет аналогично) по формуле хи-квадрат.
| Y | |||
|---|---|---|---|
| X1 | 1 | 0 | Всего |
| 1 | 1 | 1 | 2 |
| 0 | 1 | 1 | 2 |
| Всего | 2 | 2 | 4 |
Легко посчитать, что хи-квадрат будет равен 0, то есть никакой корреляции между фичей и целевой переменной не покажет.
Пример утрирован, но он хорошо показывает, что методы фильтрации не способны уловить совместное влияние нескольких фич на целевую переменную.
Wrapper methods
Суть этой категории методов в том, что классификатор запускается на разных подмножествах фич исходного тренировочного сета. После чего выбирается подмножество фич с наилучшими параметрами на обучающей выборке. А затем он тестируется на тестовом сете (тестовый сет не участвует в процессе выбора оптимального подмножества).
Есть два подхода в этом классе методов — методы включения (forward selection) и исключения (backwards selection) фич. Первые стартуют с пустого подмножества, куда постепенно добавляются разные фичи (для выбора на каждом шаге оптимального добавления). Во втором случае метод стартует с подмножества равного исходному множеству фич, и из него постепенно удаляются фичи, с пересчетом классификатора каждый раз.
Один из примеров таких методов — recursive feature elimination. Как следует из названия, он относится к алгоритмам постепенного исключения фич из общего пула. На питоне реализация этого алгоритма есть в библиотеке scikit-learn. Этот метод требует выбрать классификатор, с помощью которого будут оцениваться фичи, например, линейная регрессия:
from sklearn.feature_selection import RFE
from sklearn.linear_model import LinearRegression
data= load_data()
X = data["data"]
Y = data["target"]
lr = LinearRegression()
#select 5 the most informative features
rfe = RFE(lr, 5)
selector = rfe.fit(X,Y)
Хотя метод исключения лучше отслеживает взаимосвязи между фичами, он гораздо дороже вычислительно. Впрочем, все wrapper methods требуют гораздо больших вычислений, чем методы фильтрации. К тому же в случае большого количества фич и небольшого размера тренировочного сета эти методы имеют опасность переобучения.
Встроенные методы (embedded methods)
И наконец, встроенные методы, которые позволяют не разделять отбор фич и обучение классификатора, а производят отбор внутри процесса расчета модели. К тому же эти алгоритмы требуют меньше вычислений, чем wrapper methods (хотя и больше, чем методы фильтрации).
Основным методом из этой категории является регуляризация. Существуют различные ее разновидности, но основной принцип общий. Если рассмотреть работу классификатора без регуляризации, то она состоит в построении такой модели, которая наилучшим образом настроилась бы на предсказание всех точек тренировочного сета.
Например, если алгоритм классификации линейная регрессия, то подбираются коэффициенты полинома, который аппроксимирует зависимость между фичами и целевой переменной. В качестве оценки качества подобранных коэффициентов выступает среднеквадратичная ошибка (RMSE). Т.е. параметры подбираются так, чтобы суммарное отклонение (точнее суммарный квадрат отклонений) у точек предсказанных классификатором от реальных точек было минимальным.
Идея регуляризации в том, чтобы построить алгоритм минимизирующий не только ошибку, но и количество используемых переменных.
Метод регуляризации Тихонова (ridge regression)
Рассмотрим все так же на примере линейной регрессии. Если в тестовом сете дана матрица фич A и вектор целевой переменной b, то мы ищем решение в виде Ax=b. В процессе работы алгоритма минимизируется такое выражение:
Где первое слагаемое это как раз среднеквадратичная ошибка, а второе — регуляризирующий оператор (сумма квадратов всех коэффициентов, умноженная на альфа). В процессе работы алгоритма размеры коэффициентов будут пропорциональны важности соответствующих переменных, а перед теми переменными, которые дают наименьший вклад в устранение ошибки, станут околонулевые.
Пара слов о параметре альфа. Он позволяет настраивать вклад регуляризирующего оператора в общую сумму. С его помощью мы можем указать приоритет — точность модели или минимальное количество используемых переменных.
Если мы хотим использовать линейную регрессию с регуляризацией Тихонова, то нет необходимости изобретать велосипед. В библиотеке scikit-learn есть модель под названием Ridge regression, которая включает в себя этот тип регуляризации.
from sklearn.linear_model import Ridge
data= load_data()
X = data["data"]
y = data["target"]
clf = Ridge(alpha=1.0)
clf.fit(X, y)
Обратите внимание на возможность вручную настроить параметр альфа.
LASSO
Аналогичен предыдущему во всем кроме отличия в регуляризирующем операторе. Он представляет собой не сумму квадратов, а сумму модулей коэффициентов. Несмотря на незначительность различия, свойства отличаются. Если в ridge по мере роста альфа все коэффициенты получают значения все ближе к нулевым, но обычно при этом все-таки не зануляются. То в LASSO с ростом альфа все больше коэффициентов становятся нулевыми и совсем перестают вносить вклад в модель. Таким образом, мы получаем действительно отбор фич. Более значимые фичи сохранят свои коэффициенты ненулевыми, менее значимые — обнулятся. Подробнее послушать об этих свойствах и взглянуть на графики (а за одно узнать про Elastic Net, на котором я не стану останавливаться) можно, например, в этой лекции.
Использование этого метода с помощью библиотеки scikit-learn так же идентично предыдущему методу. Только Ridge заменяется на Lasso.
Таким образом, регуляризация — это своеобразный штраф за излишнюю сложность модели, который позволяет защитить себя от перетренировки в случае наличия среди фич мусорных. Не стоит думать, что регуляризация бывает только в линейных моделях, и для бустинга и для нейросетей существуют свои методы регуляризации.
Из минусов регуляризации можно отметить тот факт, что модель строится на всем массиве фич а значит, она не ускоряет работу классификатора. Но в общем случае этот метод способен лучше уловить взаимозависимости переменных, чем методы фильтрации.
В заключение
Я не буду здесь писать выводы о критериях выбора того или иного метода в конкретной ситуации. В большинстве случаев проще и удобнее всего будет обратиться к встроенным методам. В случае если нужна наглядность — методы фильтрации могут ее обеспечить. Остальное, я думаю, вопрос практики.
Буду рада услышать комментарии. Если, по вашему мнению, в тексте есть неточность, чего-то не хватает, что-то непонятно, хотите поделиться своим практическими наблюдениями — пишите.
Ссылки
stats.stackexchange.com/questions/13389/information-gain-mutual-information-and-related-measures
www.coursera.org/course/mmds
www.cs.binghamton.edu/~lyu/publications/Gulgezen-etal09ECML.pdf
habrahabr.ru/company/mailru/blog/254897
machinelearningmastery.com/an-introduction-to-feature-selection
ocw.jhsph.edu/courses/fundepiii/pdfs/lecture17.pdf
blog.datadive.net/selecting-good-features-part-iv-stability-selection-rfe-and-everything-side-by-side
ai.stanford.edu/~ronnyk/wrappersPrint.pdf
www.math.kent.edu/~reichel/publications/modtikh.pdf
scikit-learn.org/stable/modules/linear_model.html
Комментарии (21)

stepanovD
17.08.2015 16:29Спасибо!
Возникли следующие вопросы:
- По какому принципу выбирается целевая переменная, что делать в случае высокой размерности фич?
- Как оценивается точность отбора фич?
- Довольно часто после выделения фич применяется не классификация, а кластеризация. Как от этого может поменяться выбор метода и как оценить качество кластеризации?

Jaylla
17.08.2015 19:21Постараюсь ответить (если я неправильно пойму какой-либо вопрос – поправьте меня).
1. У нашего анализа, как правило, есть цель – предсказать что-либо (погоду, цену на рынке, тип документа, объект на фотографии). Она и обуславливает выбор целевой переменной, т.е. объекта предсказания. При слишком большом количестве фич (большой размерности массива) можно избавиться от части используя методы фильтрации, можно уменьшить размерность (dimensionality reduction методы, например, PCA).
2. Тут довольно просто. Следует использовать кросс валидацию и оставлять некоторое количество как тестовый сет. На нем можно оценить эффективность, сравнив точность классификатора на полном и на урезанном массиве фич.
3. Самый сложный вопрос потому, что самый объемный. Я не смогу сейчас описать все возможные методы и нюансы, связанные с unsupervised learning (как правило, кластеризация используется в этом случае). Для такого случая для уменьшения размерности фич можно применять feature extraction методы.
stepanovD
18.08.2015 09:20- Извиняюсь, это я не сразу понял, что вы назвали целевой переменной. Я подумал, что целевая переменная — это одна из компонент дескриптора фичи. Если рассмотреть область поиска изображений, то в случае с SIFT это одна из 128 компонент.
- Вот такой подход меня всегда смущает. Насколько корректно оценивать качество отбора по результатам классификации? Ведь результат классификации очень сильно зависит от самого классификатора. И при выборе неподходящего метода классификации можно получить результаты далекие от правды.
- А разве перед отбором фич их не надо получить? Вы же в любом случае будете применять feature extraction методы.
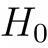
kxx
17.08.2015 17:49+1Проблема отбора фич очень неоднозначная — прежде всего потому, что разные методы могут давать диаметрально противоположные результаты: univariate filters дают один набор переменных, а, скажем, feature selection using genetic algorithms — совершенно другой. В R для модуля caret есть неплохой мануал по этой теме. Вот еще практическая реализация простого и относительно универсального метода «перетасовок».

Jaylla
17.08.2015 19:11Постараюсь ответить (если я неправильно пойму какой-либо вопрос – поправьте меня).
1. У нашего анализа, как правило, есть цель – предсказать что-либо (погоду, цену на рынке, тип документа, объект на фотографии). Она и обуславливает выбор целевой переменной, т.е. объекта предсказания. При слишком большом количестве фич (большой размерности массива) можно избавиться от части используя методы фильтрации, можно уменьшить размерность (dimensionality reduction методы, например, PCA).
2. Тут довольно просто. Следует использовать кросс валидацию и оставлять некоторое количество как тестовый сет. На нем можно оценить эффективность, сравнив точность классификатора на полном и на урезанном массиве фич.
3. Самый сложный вопрос потому, что самый объемный. Я не смогу сейчас описать все возможные методы, связанные с unsupervised learning (как правило, кластеризация используется в этом случае). Для такого случая для уменьшения размерности фич можно применять feature extraction методы.

Jaylla
17.08.2015 19:21Ошиблась с ответом, извините.
Методы фильтрации не идеальны, поэтому, разумеется, могут давать разный результат. Хотя на счет диаметрально мне сложно поверить. У вас были такие случаи?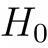
kxx
17.08.2015 23:54+1Из сравнительно недавних — соревнование на Kaggle: в датасете 41 фича, из них 37 анонимные (P* — неизвестно, что они на самом деле означают).
FS with genetic algorithm (5-fold CV): «P5»,«P13»,«P14»,«P16»,«P17»,«P18»,«P19»,«P20»,«P21»,«P23»,«P24»,«P27»,«P28»,«P30»,«P32»,«P33»,«P36».
FS with simulated annealing (5-fold CV): «P1»,«P2»,«P3»,«P4»,«P7»,«P8»,«P13»,«P17», «P20»,«P21»,«P22»,«P28»,«P34»,«P35»,«P37».
Нет, множества, конечно, в чем-то пересекаются, но сделать однозначный выбор на основе этих данных весьма трудно.

SKolotienko
18.08.2015 16:13+1Можно придумать искусственный пример, когда разные алгоритмы (или разные реализации одного алгоритма) в итоге сойдутся к разным наборам фич. Например, взять исходное множество признаков и «продублировать» каждый признак. Т.к. в итоге получится минимум по два полностью скореллированных признака, то алгоритмы типа mrmr могут выбрать случайный из них.

Alexey_mosc
17.08.2015 18:24-1Обзор неплох, но слегка поверхностен. Мне было интересно почить про методы включения и ислючения, но не хватает обзора их недостатков.
Для взаимной информации, названной у вас information gain, как меры связи между предиктором и зависимой переменной (кстати, не упомянули, что ее можно посчитать и между набором предикторов и зависимой переменной), характерна одна большая проблема, которая, кстати, решается (об этом также не сказано): предиктор может обладать настолько большой энтропией, что будет прекрасно якобы детерминировать зависимую переменную на обучающей выборке, однако вся кажущаяся детерминированность пропадет при проверке на независимой выборке. Пример: есть 100 наблюдений, предиктор с 90 уровнями встречающимися в тесте.
Для метода mRmR характерна одна тоже большая проблема (расчет получается очень не точный): брать сумму значений взаимной информации для каждой пары предиктор-зависимая переменная корректно лишь в том случае, если предикторы независимы между собой. Иначе можно получить огромную избыточную взаимную информацию. Также не корректно усреднять взаимную информацию между предикторами, когда есть корректный метод, называемый multiinformation.
Вообще все перечисленные методы субоптимальны и можно придумать разновидность wrapper-метода, который победит все перечисленные недостатки, кроме, пожалуй, стоимости вычислений.
Jaylla
17.08.2015 19:44Я и так боялась, что объем получился слишком большой.
Вы правы, что в смысле точности никакой из методов фильтрации не сравнится с wrapper. Но недостаток wrapper-методов (стоимость вычислений) очень весомый. Если есть возможность тренировать модель на всем объеме фич, то проще и лучше использовать классификатор с регуляризацией. Это будет дешевле в смысле вычислений, и точность не хуже.
Ниша методов фильтрации — случаи, когда тренировать модель на всем объеме фич мы просто не можем – памяти не хватает. Тогда другие методы не сработают.

SKolotienko
18.08.2015 16:29+1Вопрос про mrmr: вы пишете, что приведенные методы фильтрации, к которым также относится mrmr, хороши тем, что их стоимость зависит линейно от количества фич. Но разве алгоритм mrmr работает за линейное время?
Правильно ли я понимаю, как работает алгоритм:
1) Проходим по всем признакам, для каждого признака считаем выражение с учетом текущего множества «отобранных».
2) Выбираем признак, для которого значение этого выражения было максимально.
3) Если добавление нового признака улучшает значение функции, то добавляем признак в множество «отобранных» и возвращаемся к пункту 1.
То есть, так как формула считается за O(|S|^2), при этом она на каждый новый признак будет вызываться порядка |X|(кол-во признаков) раз, а в худшем случае мы будем добавлять все признаки из X, то алгоритм работает за квадратичное от количества признаков время. Или я что-то не так понял?
SKolotienko
18.08.2015 16:38Edit: не квадратичное, а четвертая степень.
И даже если есть какие-либо методы всё это дело ускорить, не вижу возможности сделать алгоритм быстрее, чем квадратичным — при рассчете redundancy нужно пройтись по всем парам признаков.
Alexey_mosc
18.08.2015 17:23Видимо из-за неточности в обзоре mRmR выдан за фильтрующий метод отбора, тогда как он суть метод расчета фитнесс функции.
mRmR можно в качестве фитнесс функции подставить в любой алгоритм отбора информативных признаков.
Jaylla
18.08.2015 19:29mRmR можно в качестве фитнесс функции подставить в любой алгоритм отбора информативных признаков
А можно подробнее про это? Может быть, вы можете посоветовать каую-нибудь статью
Alexey_mosc
18.08.2015 19:57Я статью не могу порекомендовать.
Пример приведу, который мне близко знаком.
mRmR относится к классу фитнес функций, где оценка проводится для взаимодействий сразу всех предикторов, выбранных алгоритмом отобора фичей. Я пробовал применять информационную метрику (не mRmR, а более точный самописный метод) с использованием генетического алгоритма и имитации отжига. Переменные (предикторы и зависимая) должны быть дискретны, а если некоторые из них непрерывны, нужно сделать процесс дискретизации. Далее алгоритм отбора создает множество векторов предикторов, размерность которых меньше (или равна) общему количеству предикторов. Но чтобы информационные метрики работали на благо хозяйства, нужно еще их корректировать. Это отдельная большая тема.
Можно таким же образом использовать mRmR, например, в паре с алгоритмом включения или исключения предикторов.
Сама суть — мы меряем не какие-то линейные зависимости, которые могут лишь частично описать все многообразие зависимостей в задаче, а взаимную информацию, которая способна померять зависимость произвольной формы, хоть шестилистный клевер в 10 мерном пространстве.
Но я вообще против применения mRmR, так как он методологически не совсем верен. Когда я первый раз про него прочитал и посмотрел формулу, то сразу положил на него.
В чем его неверность:
Например, средняя взаимная информация для каждой пары предиктор-выход будет почти наверное посчитана неверно в том смысле, что информация, передаваемая набором предикторов может быть либо больше, либо меньше суммы взаимных информаций, передаваемых каждым предиктором.
А еще более подробно: если предикторы взаимосвязаны (взаимная информация между ними не нулевая), то их сумма взаимной информации будет больше (избыточнее), чем взаимная информация их взаимодействий. А если переменные по отдельности не влияют на зависимую переменную, но их взаимодействия влияют, то взаимная информация, передаваемая их взаимодействием, будет больше, чем их атомарные взаимные информации.

Jaylla
18.08.2015 17:34+1Все верно, спасибо за замечание (чуть позже исправлю в статье). Статья писалась не линейно, и кусок про mRmR появился позже. Мои слова про сложность методов фильтрации верны для взаимной информации, хи-квадрата, но не для mRmR.


poddubny
Спасибо за статью!
А чем отличается расчет information gain от простого расчета корреляции между фичами и целевой переменной?
Jaylla
Вам спасибо за комментарий.
Если под корреляцией вы подразумеваете линейный коэффициент корреляции, то метод расчета у них совсем разный. Я его не использовала и даже в статьях его упоминаний не видела, так что ничего не могу сказать про эффективность, к сожалению.