Как известно, и мы, и американцы, установили на Луне уголковые отражатели, благодаря чему с помощью лазера можно измерять расстояние до неё с точностью до уже сантиметров.

Уголковый отражатель отражает падающий от излучателя луч строго в обратном направлении. Но это так, если излучатель и уголковый отражатель взаимно неподвижны. При локации Луны имеем, что Луна движется по орбите радиусом 380000 км со скоростью около 1,3 км/сек, и поверхность земли с излучателем и приёмником тоже движется, если я правильно понял, в ту же сторону со скоростью от 0,46 км/сек на экваторе до в два раза меньшего значения на 60-й широте.
Кроме того, законы отражения от движущегося зеркала отличаются для случаев, если свет волна и если свет частица. Насколько же промахивается отражённый от Луны луч и можно ли это заметить? Вычислим это, причём не выходя за рамки школьной математики. Автор будет благодарен за замечания и указания об ошибках.
Расчёт двойного отражения от движущихся зеркал уголкового отражателя не кажется простой задачей. Например, в статье Б.М.Болотовского и С.Н.Столярова "Отражение света от движущегося зеркала и родственные задачи" рассматривается только отражение от зеркала движущегося перпендикулярно своей поверхности путём пересчёта характеристик электромагнитных полей выражаемых уравнениями Максвелла. При этом обоснование метода излагается на 14 страницах.
Попробуем решить задачу для движущегося наклонного зеркала анализируя движение фронтов падающей и отражённой волн. Рассмотрим участок AO фронта волны шириной S. Луч (синие линии со стрелками) падает на зеркало (голубая линия) под углом ? от вектора скорости его движения V. Отражается он под углом ? (зелёная дуга). Угол наклона нормали зеркала к вектору скорости равен ?. Это конечно не полная 3D-схема, но для уголкового отражателя сгодится.

После попадания в зеркало края фронта AO волны в точке O, другой его край продолжает движение пока не попадёт в зеркало в точке C. На это потребуется время t и лучи, падающий и отражённый, пройдут расстояние c•t, где с — скорость света. Следовательно, BO = AC. Это значит, что прямоугольные треугольники OAC, ODC и OBC равны.
Зеркало за это время сдвинется на расстояние V•t, и часть расстояния до точки C добавится из-за наклона зеркала на угол ?.
Рис.1
Перейдём к световым единицам измерений. Положим св.ед.скорости = ед.скорости/ скорость света и тогда V>?. Мы знаем, что движущееся зеркало сокращается пропорционально коэффициенту Лоренца. Следовательно, угол ? связан с углом ?0 наклона зеркала в его собственной системе отсчёта формулой (1). На схеме рис.1 расстояние AC выражается формулой (2). Из (2) и (3) вычислим c•t и y, и подставим в уравнение (4), откуда найдём значение x по формуле (6) и далее c•t из (2). Затем вычислим tg ? по формуле (7). Из чертежа следует, что углы падения ? и отражения ? связаны соотношением (8), которое и является решением задачи.
Уравнение (9) получено из мысленного эксперимента, заключающегося в том, что позиции источника света, зеркала и отражённого «зайчика» на экране, зафиксированные на лабораторном столе при его неподвижности, не должны измениться, когда он начнёт двигаться. Это следует из принципа относительности. Значения, вычисленные по формулам (8), удовлетворяют уравнению (9) при всех разумных сочетаниях углов падения, наклона зеркала и скорости. Естественно, при нулевом наклоне зеркала результаты совпадают с расчетами по формулам Болотовского и Столярова.

 Для расчёта отклонения отражённого луча от исходного направления можно воспользоваться формулой углов отражения при нулевом наклоне зеркала. Дело в том, что если сверху к вертикальному зеркалу приставить горизонтальное, то мы получим уголковый отражатель при его предельном угле поворота. Результаты показаны на рис.2. Прямые расчёты математической модели движущегося уголкового отражателя по формуле (8) показали независимость угла отклонения отражённого луча от поворота отражателя.
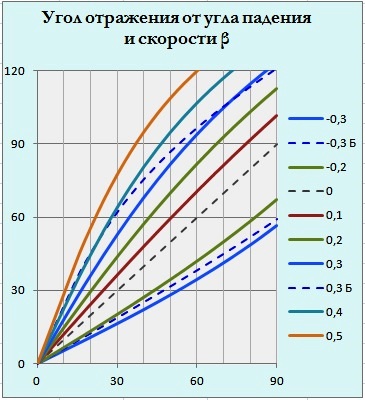
Для расчёта отклонения отражённого луча от исходного направления можно воспользоваться формулой углов отражения при нулевом наклоне зеркала. Дело в том, что если сверху к вертикальному зеркалу приставить горизонтальное, то мы получим уголковый отражатель при его предельном угле поворота. Результаты показаны на рис.2. Прямые расчёты математической модели движущегося уголкового отражателя по формуле (8) показали независимость угла отклонения отражённого луча от поворота отражателя.
Графики приведены для диапазона скоростей зеркала от встречного движения -0,3 световой до +0,5 вдогонку.
Рис.2
Кстати, при отражении луча догоняющего зеркало, угол отражения может превышать 90°, как это отображено на рис.1. Для сравнения приведены графики отклонения для баллистической теории света отображённые синими пунктирными линиями для скоростей -0,3 и +0,3 световой и отмеченных литерой «Б». В этой теории свет считается частицами, а теория относительности отвергается. Расчёт проводился согласно школьной методике. Как видим, отклонения в таком случае будут иные, так что прямой эксперимент мог бы подтвердить или отвергнуть баллистическую теорию.
Итак, насколько же «зайчик» от уголкового отражателя на Луне отклонится от места установки лазера на Земле? Расчёты показывают, что максимальный угол отклонения, в точке верхней кульминации Луны, будет 0,0005 градуса. На Земле отклонение составит примерно 3,3 км в сторону движения Луны по орбите, но за 2,5 секунды, пока импульс возвратится, земная поверхность подъедет почти на километр, так что итоговое отклонение составит около 2,5 км. Поскольку размер отражённого лазерного зайчика на земной поверхности составляет порядка 15 км, заметить сам факт отклонения пока невозможно. И, кстати, отклонение по баллистической теории для этих условий совпадает с отклонением по СТО до 8-го знака (т.е. расхождение не более 10 метров).

Уголковый отражатель отражает падающий от излучателя луч строго в обратном направлении. Но это так, если излучатель и уголковый отражатель взаимно неподвижны. При локации Луны имеем, что Луна движется по орбите радиусом 380000 км со скоростью около 1,3 км/сек, и поверхность земли с излучателем и приёмником тоже движется, если я правильно понял, в ту же сторону со скоростью от 0,46 км/сек на экваторе до в два раза меньшего значения на 60-й широте.
Кроме того, законы отражения от движущегося зеркала отличаются для случаев, если свет волна и если свет частица. Насколько же промахивается отражённый от Луны луч и можно ли это заметить? Вычислим это, причём не выходя за рамки школьной математики. Автор будет благодарен за замечания и указания об ошибках.
Расчёт двойного отражения от движущихся зеркал уголкового отражателя не кажется простой задачей. Например, в статье Б.М.Болотовского и С.Н.Столярова "Отражение света от движущегося зеркала и родственные задачи" рассматривается только отражение от зеркала движущегося перпендикулярно своей поверхности путём пересчёта характеристик электромагнитных полей выражаемых уравнениями Максвелла. При этом обоснование метода излагается на 14 страницах.
Попробуем решить задачу для движущегося наклонного зеркала анализируя движение фронтов падающей и отражённой волн. Рассмотрим участок AO фронта волны шириной S. Луч (синие линии со стрелками) падает на зеркало (голубая линия) под углом ? от вектора скорости его движения V. Отражается он под углом ? (зелёная дуга). Угол наклона нормали зеркала к вектору скорости равен ?. Это конечно не полная 3D-схема, но для уголкового отражателя сгодится.

После попадания в зеркало края фронта AO волны в точке O, другой его край продолжает движение пока не попадёт в зеркало в точке C. На это потребуется время t и лучи, падающий и отражённый, пройдут расстояние c•t, где с — скорость света. Следовательно, BO = AC. Это значит, что прямоугольные треугольники OAC, ODC и OBC равны.
Зеркало за это время сдвинется на расстояние V•t, и часть расстояния до точки C добавится из-за наклона зеркала на угол ?.
Рис.1
Перейдём к световым единицам измерений. Положим св.ед.скорости = ед.скорости/ скорость света и тогда V>?. Мы знаем, что движущееся зеркало сокращается пропорционально коэффициенту Лоренца. Следовательно, угол ? связан с углом ?0 наклона зеркала в его собственной системе отсчёта формулой (1). На схеме рис.1 расстояние AC выражается формулой (2). Из (2) и (3) вычислим c•t и y, и подставим в уравнение (4), откуда найдём значение x по формуле (6) и далее c•t из (2). Затем вычислим tg ? по формуле (7). Из чертежа следует, что углы падения ? и отражения ? связаны соотношением (8), которое и является решением задачи.
Уравнение (9) получено из мысленного эксперимента, заключающегося в том, что позиции источника света, зеркала и отражённого «зайчика» на экране, зафиксированные на лабораторном столе при его неподвижности, не должны измениться, когда он начнёт двигаться. Это следует из принципа относительности. Значения, вычисленные по формулам (8), удовлетворяют уравнению (9) при всех разумных сочетаниях углов падения, наклона зеркала и скорости. Естественно, при нулевом наклоне зеркала результаты совпадают с расчетами по формулам Болотовского и Столярова.

 Для расчёта отклонения отражённого луча от исходного направления можно воспользоваться формулой углов отражения при нулевом наклоне зеркала. Дело в том, что если сверху к вертикальному зеркалу приставить горизонтальное, то мы получим уголковый отражатель при его предельном угле поворота. Результаты показаны на рис.2. Прямые расчёты математической модели движущегося уголкового отражателя по формуле (8) показали независимость угла отклонения отражённого луча от поворота отражателя.
Для расчёта отклонения отражённого луча от исходного направления можно воспользоваться формулой углов отражения при нулевом наклоне зеркала. Дело в том, что если сверху к вертикальному зеркалу приставить горизонтальное, то мы получим уголковый отражатель при его предельном угле поворота. Результаты показаны на рис.2. Прямые расчёты математической модели движущегося уголкового отражателя по формуле (8) показали независимость угла отклонения отражённого луча от поворота отражателя. Графики приведены для диапазона скоростей зеркала от встречного движения -0,3 световой до +0,5 вдогонку.
Рис.2
Кстати, при отражении луча догоняющего зеркало, угол отражения может превышать 90°, как это отображено на рис.1. Для сравнения приведены графики отклонения для баллистической теории света отображённые синими пунктирными линиями для скоростей -0,3 и +0,3 световой и отмеченных литерой «Б». В этой теории свет считается частицами, а теория относительности отвергается. Расчёт проводился согласно школьной методике. Как видим, отклонения в таком случае будут иные, так что прямой эксперимент мог бы подтвердить или отвергнуть баллистическую теорию.
Итак, насколько же «зайчик» от уголкового отражателя на Луне отклонится от места установки лазера на Земле? Расчёты показывают, что максимальный угол отклонения, в точке верхней кульминации Луны, будет 0,0005 градуса. На Земле отклонение составит примерно 3,3 км в сторону движения Луны по орбите, но за 2,5 секунды, пока импульс возвратится, земная поверхность подъедет почти на километр, так что итоговое отклонение составит около 2,5 км. Поскольку размер отражённого лазерного зайчика на земной поверхности составляет порядка 15 км, заметить сам факт отклонения пока невозможно. И, кстати, отклонение по баллистической теории для этих условий совпадает с отклонением по СТО до 8-го знака (т.е. расхождение не более 10 метров).


valemak
Я наивно полагал, что уголковые отражатели абсолютно неоспоримый аргумент, железобетонно доказывающий, что американцы были на Луне. Типа, шах и мат вам, амерканофобы, ага.
Но в споре с «нелетальщиками» этот номер не прошёл. Они мне «доказали», что вся поверхность Луны сама по себе отражает лазерные вспышки и лазерная локация наличия зеркал в местах посадок «Аполлонов» не доказывает.
После этого я окончательно понял, что «лунная афёра» для лунозаговорщиков это вопрос веры, и спорить с ними, что-то им доказывать — совершенно бесполезная трата времени.
ukhanov
В первом же предложении: «Как известно, и мы, и американцы, установили на Луне уголковые отражатели...»
На всякий случай: я не отношусь ни к какой из этих партий.
valemak
Все люди делятся на три группы — те, кто считают что Земля геоид, те кто считают, что Земля плоская и, наконец, те, кто не принадлежит ни к одной из этих партий :-)
Zenitchik
Земля в любом случае — геоид. Даже если плоская.
Хотя, нормальные люди, всё-таки считают геоид близким к эллипсоиду.
Sergey_Kovalenko
Все люди считают себя нормальными, разве нет?
Astroscope
Нет. :)
ukhanov
На всякий случай: я ЗНАЮ, что Земля — геоид близкий в каком-то смысле к шару.
И?
ukhanov
К господам минусующим:
1) я указал valemak на то, что он не удосужился прочитать первое предложение, которое полностью разрушает его аргумент;
2) я сказал, что не собираюсь участвовать ни в каких дебатах на поднятую им тему;
3) он притянул за уши плоскоземельщиков, и… каким-то финтом записал туда и меня.
Собственно поэтому к вам вопрос: а вы точно читать умеете?
И да, ответ меня не интересует, потому что он нужен только вам.
rishat_edison
delete
Astroscope
вступить в эту третью партиюпогуглить по ключевым словам «convex earth». :-)sim2q
pavlentich
неужели им время между отправкой и примем отраженного сигнала тоже ничего не говорит??? ну ладно, допустим для одной точки не скажет, а ведь если из разных километров в 200, можно ведь и радиус земли оценить, а если из четырех то и кусок сферы можно получить…
Serdechnyj Автор
Поскольку световое пятно от лазера на Луне несколько километров в диаметре, то при отражении от её поверхности перепады высот могут быть десятки метров. Соответственно принимаемый отклик будет размыт по времени.
Но поскольку, по некоторым источникам, сейчас измеряют расстояние до Луны уже в пределах метра, то, полагаю, придётся признать, что измеряется отклик именно от отражателя.
Teemon
Я тоже рассуждал в этом ключе «шах вам и мат», потом перешел на уровень рассуждений о том, существуют ли какие-либо средства доказательства какого-либо фактического события вообще?
В данном случае ведь действительно можно сказать, что напирмер, отражатели закинули а людей не было. Или фото — фотошоп. Или если тебя отправить на луну и ты увидишь следы глазами — что следы специально нашлёпали роботами чтобы ввести в заблуждение.
В связи с чем вопрос — а существуют ли некие фальсифицируемые или как правильно сказать эксперименты, что либо доказывающие в прошлом, а не настоящем? Неужели получается, только лично наблюдая через средства наблюдение в «реалтайме» можно считать, что событие фактически случается, а всё остальное — можно принимать «на веру» с различной степенью веры в это?
valemak
Я «лунозаговорщикам» тоже пытался задавать подобный вопрос. Попросил их чётко сказать — если им не подходят все нынешние аргументы в пользу НАСА, то какого рода доказательств они ожидают в принципе? Что именно нужно для них доказать, чтобы завершить споры? Чтобы именно бы их убедило? Или они просто тупо будут огульно отрицать вообще всё?
Разумеется, внятного ответа я от них не получил. Им нет смысла что-то доказывать, они будут воспринимать абсолютно любые доказательства высадки Аполлонов как ложные. Нет какого-либо доказательства, которое ими воспримется как окончательное.
Если удаётся убедительно опрокинуть какой-нибудь их маразм, то они тогда переключаются на другой довод. И спор становится бесконечным — получается что нужно опровергнуть не какой-то их конкретный довод — нужно опровергнуть ВСЕ их доводы, а если этим заниматься — то и всей жизни не хватит.
nvksv
Задачи такого рода, насколько я знаю, принято решать в инерциальной системе отсчета, в которой зеркало неподвижно. При этом все эффекты, связанные с движениями Земли и Луны, просчитываются элементарно, даже с учетом релятивизма. Источник фотона был в одной точке, затем фотон отразился и прилетел в другую точку, куда за время его полета передвинулся источник. Релятивистский эффект Доплера, релятивистское сжатие расстояний и соответственные изменения углов и т.д. Ничего больше не надо.
Зачем что-то усложнять? Или Вы хотите проверить теорию относительности на прочность?
Serdechnyj Автор
Ну вообще-то, все опубликованные расчёты отражения от движущегося зеркала, которые удалось найти мне, гораздо сложнее моих. Да и то наиболее часто ссылаются на упомянутую статью Болотовского и Столярова.
И, кстати, я не сомневаюсь в правильности формул выведенных по СТО. Наоборот, я показываю в чём состоит сама физика этих явлений. И тогда можно всё рассчитать простейшим образом в реальном пространстве, не используя преобразований Лоренца для пространства Минковского.
Osnovjansky
Или «стрелять» лазером, установленным на машину из нескольких точек по-очереди, с шагом хоть 100 м (при неподвижном приемнике)?
Зная «края» получим куда отклонилась центральная ось.
Только тогда нужно при первоначальной калибровке отражателя аналогично определить куда именно он отражает.
Javian
Эти приёмники являются телескопами с зеркалом под 2 метра. Уникальные вещи сами по себе. И рядом таких же нет.
Serdechnyj Автор
Во первых, луч от лазера передают к Луне через сколько-то метровый телескоп. И то световое пятно на Луне оказывается диаметром в несколько км. И ещё при посылке импульса надо точно прицелится с упреждением по времени, иначе не попасть в отражатель. Полагаю, стреляют очередями. Так что возить лазер не получится.
А во-вторых, задачей вообще локации Луны является уточнение её траектории и распределения масс в ней, а искать угол отклонения луча из-за её движения никому пока не надо. Это уж я из чистого любопытства решил его оценить. И, как и ожидалось, отклонение оказалось слишком мало, чтобы его следовало принимать во внимание.
Osnovjansky
А не подскажите, где почитать? Почему приёмник — телескоп — понятно. А вот передатчик — не совсем.
Shkaff
Ну логика простая: фокус луча должен быть как можно ближе к отражающему зеркалу на Луне, в идеале прямо на нем. Тогда луч будет симметричен. Чтобы сделать такой фокус — нужен большой телескоп. Так что в реальности используют один и тот же телескоп для отправки и детектирования. Например, тут картинка 1.
Osnovjansky
Спасибо, почитаю. Просто мне казалось, что проще взять лазер побольше, чем согласовывать с оптикой телескопа.
Но теперь задумался, и действительно, малое пятно лазера уменьшает помехи от рельефа и помогает получить сантиметровую точность
Shkaff
«Лазер побольше» это значит зеркала и линзы. Сам по себе кристалл лазера всегда маленький. А раз нужно расширять луч с помощью зеркал и линз, почему бы не использовать лучшие доступные — в телескопе. Там вся оптическая система уже настроена для оптимальной передачи луча и фокусировки в маленькую камеру. Если по тому же пути запустить луч в обратную сторону — он из маленького лазера расширится в широкий пучок. Удобно:)
Osnovjansky
Ну, если при использовании телескопа хватает полупроводникового лазера — действительно удобно.
Я думал о всяких газовых и химических лазерах в 100… 1 000 000 Вт.
Из оптических схем лазеров, мне когда-то в Юном технике понравилась: камера лазера устроена как «стол», на котором две шеренги зеркал, между которыми луч идет зиг-загом. В итоге неплохая параллельность пучка должна получаться «сама собой». Работает ли такое в реальной жизни — не интересовался.
Shkaff
Tyusha
Там же, поди, дело не в длине фокуса, а дифракционном пределе выходного отверстия. Потому нужно побольше главное зеркало.
Shkaff
В моей голове это примерно одно и то же в данном случае, но вообще вы правы:) Чтобы обеспечить минимальный размер пятна при минимальном размере зеркала на таком расстоянии, луч по сути должен быть сколлимирован. Для него расходимость меньше, если ширина больше. Т.е. нужно большое зеркало. По идее, не будет разницы, коллимировать или фокусировать при заданной величине сигнала на детекторе, так что, наверное, они коллимируют — это проще для контроля.
Shkaff
Вот тут есть описание подробное экспериментов Apollo, включая всякие тайминги.
icelord2
не только американцы, отражатели стоят и доступны на: «Луноход-1», доставленный на Луну в рамках миссии «Луна-17», и «Луноход-2», доставленный в ходе миссии «Луна-21»,