В сложных ERP-системах многие сущности имеют иерархическую природу, когда однородные объекты выстраиваются в дерево отношений «предок — потомок» — это и организационная структура предприятия (все эти филиалы, отделы и рабочие группы), и каталог товаров, и участки работ, и география точек продаж,…

Фактически, нет ни одной сферы автоматизации бизнеса, где хоть какой-нибудь иерархии да не оказалось бы в результате. Но даже если вы не работаете «на бизнес», все равно можете легко столкнуться с иерархичными связями. Банально, даже ваше генеалогическое древо или поэтажная схема помещений в торговом центре — такая же структура.
Существует много способов хранения такого дерева в СУБД, но мы сегодня остановимся только на одном варианте:
И пока вы всматриваетесь в глубину иерархии, она терпеливо ждет, насколько же [не]эффективными окажутся ваши «наивные» способы работы с такой структурой.

Давайте разберем типовые возникающие задачи, их реализацию на SQL и попробуем улучшить их производительность.
Давайте, для определенности, примем, что эта структура у нас будет отражать подчиненность отделов в структуре организации: департаменты, дивизионы, секторы, филиалы, рабочие группы,… — как их ни назови.

Начнем с самой простой задачи — найти всех сотрудников, которые работают внутри конкретного сектора, или в терминах иерархии — найти всех потомков узла. А еще и «глубину» потомка неплохо бы получить… Все это может быть необходимо, например, для построения какой-то сложной выборки по списку ID этих сотрудников.
Все бы ничего, если этих потомков там всего пара уровней и количественно в пределах десятка, но если уровней больше 5, а потомков уже десятки — могут быть проблемы. Давайте посмотрим, как пишутся (и работают) традиционные варианты поиска «вниз по дереву». Но сначала определим, какие из узлов будут наиболее интересными для наших исследований.
Самые «глубокие» поддеревья:
Самые «широкие» поддеревья:
Для этих запросов мы воспользовались типичным рекурсивным JOIN:
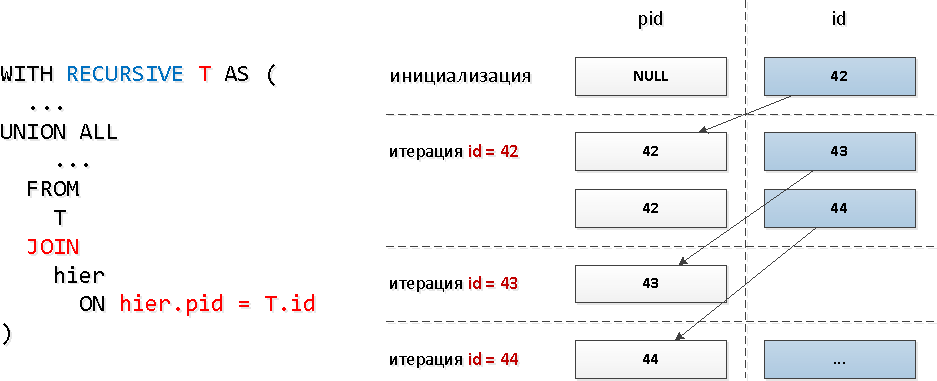
Очевидно, при такой модели запроса количество итераций будет совпадать с общим количеством потомков (а их ведь несколько десятков), и занимать это может достаточно существенные ресурсы, и, как следствие, время.
Проверим на самом «широком» поддереве:
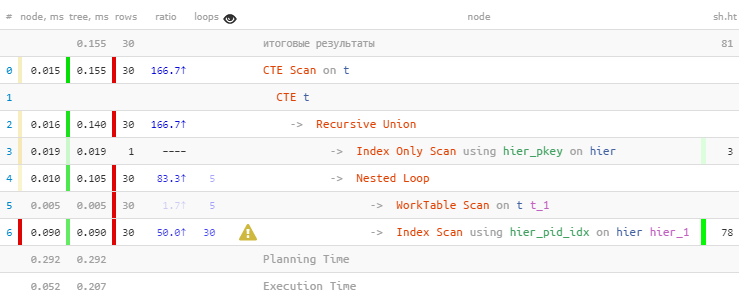
[посмотреть на explain.tensor.ru]
Как и предполагали, мы нашли все 30 записей. Но потратили на это 60% всего времени — потому что сделали при этом и 30 поисков по индексу. А меньше — можно?
А для каждого ли узла нам необходимо делать отдельный запрос к индексу? Оказывается, нет — читать из индекса мы можем сразу по нескольким ключам за одно обращение с помощью
А в каждую такую группу идентификаторов мы можем взять все найденные на предыдущем шаге ID по «узлам». То есть на каждом следующем шаге мы будем искать сразу вообще всех потомков определенного уровня.
Только, вот незадача, в рекурсивной выборке нельзя обратиться к самой себе во вложенном запросе, а нам ведь надо как-то отобрать именно только найденное на предыдущем уровне… Оказывается, сделать вложенный запрос ко всей выборке — нельзя, а вот к ее конкретному полю — можно. А это поле может быть и массивом — что нам и нужно для использования
Звучит несколько дико, но на схеме — все просто.
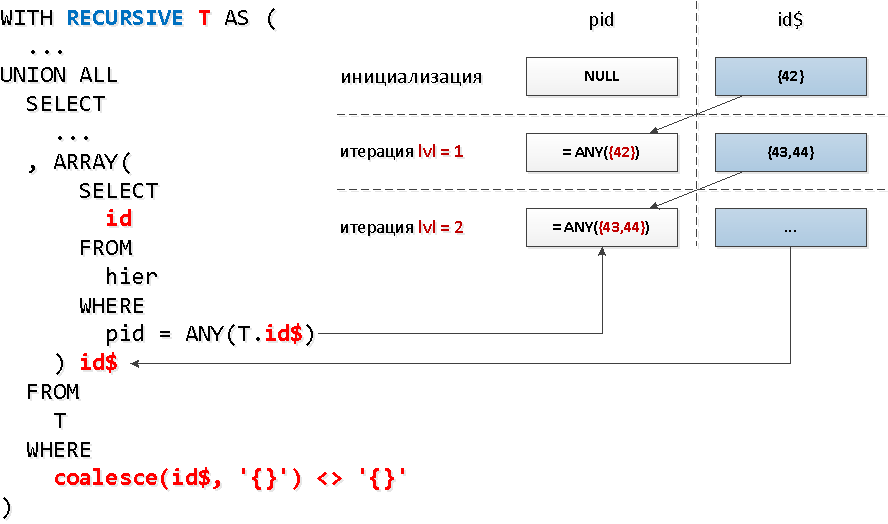

[посмотреть на explain.tensor.ru]
И тут самым важным является даже не выигрыш в 1.5 раза по времени, а что мы вычитали меньше buffers, поскольку обращений к индексу у нас всего 5 вместо 30!
Дополнительным бонусом идет тот факт, что после финального unnest идентификаторы останутся упорядочеными по «уровням».
Следующее соображение, которое поможет улучшить производительность — у «листьев» не может быть детей, то есть для них искать «вниз» вообще ничего не надо. В постановке нашей задачи это означает, что если мы шли по цепочке отделов и дошли до сотрудника, то дальше по этой ветке искать уже незачем.
Давайте введем в нашу таблицу дополнительное
Отлично! Оказывается у нас только чуть больше 30% всех элементов дерева имеют потомков.
Теперь применим несколько иную механику — соединения с рекурсивной частью через
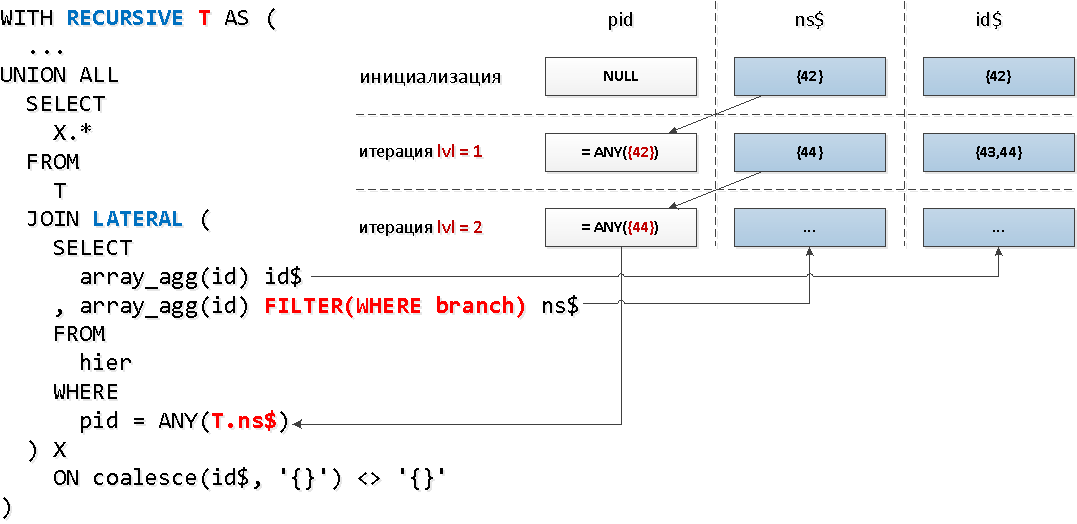

[посмотреть на explain.tensor.ru]
Мы смогли сократить еще одно обращение к индексу и выиграли более чем в 2 раза по объему вычитываемого.
Этот алгоритм будет полезен, если вам необходимо собрать записи для всех элементов «вверх по дереву», сохранив при этом информацию, каким исходным листом (и с какими показателями) вызвано его попадание в выборку — например, для формирования сводного отчета с агрегацией на узлы.
Дальнейшее стоит воспринимать исключительно как proof-of-concept, поскольку запрос получается очень уж громоздкий. Но если он доминирует в вашей базе — стоит задуматься над применением подобных методик.
Начнем с пары простых утверждений:
Теперь попробуем сконструировать нужный нам запрос.
Очевидно, что на инициализации рекурсии (куда же без нее!) нам придется вычитать записи самих листьев по набору исходных идентификаторов:
Если кому-то показалось странным, что «набор» хранится строкой, а не массивом, то этому есть простое объяснение. Для строк существует встроенная агрегирующая «склеивающая» функция
Теперь нам бы получить набор ID разделов, которые надо будет вычитать дальше. Почти всегда они будут дублироваться у разных записей исходного набора — поэтому нам бы их сгруппировать, сохранив при этом информацию о листьях-источниках.
Но тут нас поджидают три неприятности:
К счастью, все эти проблемы достаточно легко обходятся. Начнем с конца.
Вот так не работает:
А так — работает, скобочки решают!
Хм… Обращение к рекурсивной CTE не может быть во вложенном запросе. Но оно может быть внутри CTE! А вложенный запрос может обращаться уже к этой CTE!
Неприятно, но… У нас же есть простой способ, как можно сэмулировать GROUP BY с помощью
А вот так — работает!
Вот теперь мы видим, зачем числовой ID превращался в текст — чтобы их можно было склеивать через запятую!
Для финала нам осталось всего ничего:
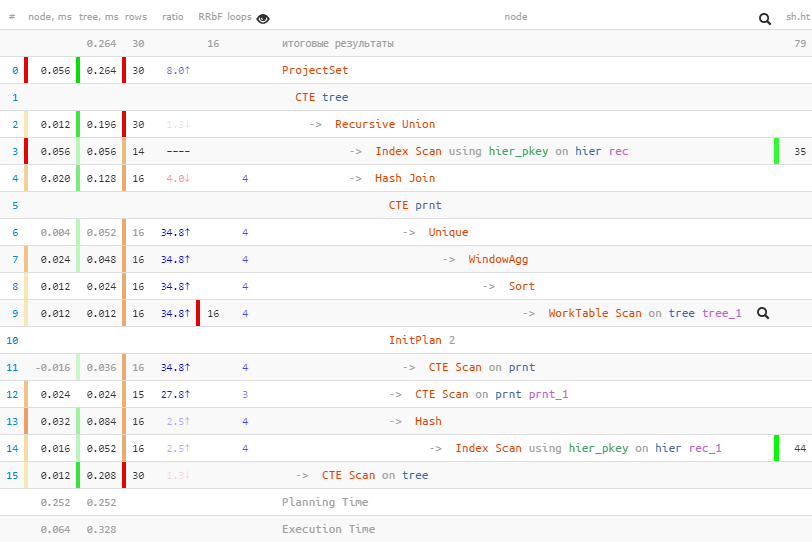
[посмотреть на explain.tensor.ru]

Фактически, нет ни одной сферы автоматизации бизнеса, где хоть какой-нибудь иерархии да не оказалось бы в результате. Но даже если вы не работаете «на бизнес», все равно можете легко столкнуться с иерархичными связями. Банально, даже ваше генеалогическое древо или поэтажная схема помещений в торговом центре — такая же структура.
Существует много способов хранения такого дерева в СУБД, но мы сегодня остановимся только на одном варианте:
CREATE TABLE hier(
id
integer
PRIMARY KEY
, pid
integer
REFERENCES hier
, data
json
);
CREATE INDEX ON hier(pid); -- не забываем, что FK не подразумевает автосоздание индекса, в отличие от PK
И пока вы всматриваетесь в глубину иерархии, она терпеливо ждет, насколько же [не]эффективными окажутся ваши «наивные» способы работы с такой структурой.

Давайте разберем типовые возникающие задачи, их реализацию на SQL и попробуем улучшить их производительность.
#1. Насколько глубока кроличья нора?
Давайте, для определенности, примем, что эта структура у нас будет отражать подчиненность отделов в структуре организации: департаменты, дивизионы, секторы, филиалы, рабочие группы,… — как их ни назови.

Сначала нагенерируем наше 'дерево' из 10K элементов
INSERT INTO hier
WITH RECURSIVE T AS (
SELECT
1::integer id
, '{1}'::integer[] pids
UNION ALL
SELECT
id + 1
, pids[1:(random() * array_length(pids, 1))::integer] || (id + 1)
FROM
T
WHERE
id < 10000
)
SELECT
pids[array_length(pids, 1)] id
, pids[array_length(pids, 1) - 1] pid
FROM
T;Начнем с самой простой задачи — найти всех сотрудников, которые работают внутри конкретного сектора, или в терминах иерархии — найти всех потомков узла. А еще и «глубину» потомка неплохо бы получить… Все это может быть необходимо, например, для построения какой-то сложной выборки по списку ID этих сотрудников.
Все бы ничего, если этих потомков там всего пара уровней и количественно в пределах десятка, но если уровней больше 5, а потомков уже десятки — могут быть проблемы. Давайте посмотрим, как пишутся (и работают) традиционные варианты поиска «вниз по дереву». Но сначала определим, какие из узлов будут наиболее интересными для наших исследований.
Самые «глубокие» поддеревья:
WITH RECURSIVE T AS (
SELECT
id
, pid
, ARRAY[id] path
FROM
hier
WHERE
pid IS NULL
UNION ALL
SELECT
hier.id
, hier.pid
, T.path || hier.id
FROM
T
JOIN
hier
ON hier.pid = T.id
)
TABLE T ORDER BY array_length(path, 1) DESC; id | pid | path
---------------------------------------------
7624 | 7623 | {7615,7620,7621,7622,7623,7624}
4995 | 4994 | {4983,4985,4988,4993,4994,4995}
4991 | 4990 | {4983,4985,4988,4989,4990,4991}
...Самые «широкие» поддеревья:
...
SELECT
path[1] id
, count(*)
FROM
T
GROUP BY
1
ORDER BY
2 DESC;id | count
------------
5300 | 30
450 | 28
1239 | 27
1573 | 25
Для этих запросов мы воспользовались типичным рекурсивным JOIN:

Очевидно, при такой модели запроса количество итераций будет совпадать с общим количеством потомков (а их ведь несколько десятков), и занимать это может достаточно существенные ресурсы, и, как следствие, время.
Проверим на самом «широком» поддереве:
WITH RECURSIVE T AS (
SELECT
id
FROM
hier
WHERE
id = 5300
UNION ALL
SELECT
hier.id
FROM
T
JOIN
hier
ON hier.pid = T.id
)
TABLE T;
[посмотреть на explain.tensor.ru]
Как и предполагали, мы нашли все 30 записей. Но потратили на это 60% всего времени — потому что сделали при этом и 30 поисков по индексу. А меньше — можно?
Массовая вычитка по индексу
А для каждого ли узла нам необходимо делать отдельный запрос к индексу? Оказывается, нет — читать из индекса мы можем сразу по нескольким ключам за одно обращение с помощью
= ANY(array).А в каждую такую группу идентификаторов мы можем взять все найденные на предыдущем шаге ID по «узлам». То есть на каждом следующем шаге мы будем искать сразу вообще всех потомков определенного уровня.
Только, вот незадача, в рекурсивной выборке нельзя обратиться к самой себе во вложенном запросе, а нам ведь надо как-то отобрать именно только найденное на предыдущем уровне… Оказывается, сделать вложенный запрос ко всей выборке — нельзя, а вот к ее конкретному полю — можно. А это поле может быть и массивом — что нам и нужно для использования
ANY.Звучит несколько дико, но на схеме — все просто.

WITH RECURSIVE T AS (
SELECT
ARRAY[id] id$
FROM
hier
WHERE
id = 5300
UNION ALL
SELECT
ARRAY(
SELECT
id
FROM
hier
WHERE
pid = ANY(T.id$)
) id$
FROM
T
WHERE
coalesce(id$, '{}') <> '{}' -- условие выхода из цикла - пустой массив
)
SELECT
unnest(id$) id
FROM
T;
[посмотреть на explain.tensor.ru]
И тут самым важным является даже не выигрыш в 1.5 раза по времени, а что мы вычитали меньше buffers, поскольку обращений к индексу у нас всего 5 вместо 30!
Дополнительным бонусом идет тот факт, что после финального unnest идентификаторы останутся упорядочеными по «уровням».
Признак узла
Следующее соображение, которое поможет улучшить производительность — у «листьев» не может быть детей, то есть для них искать «вниз» вообще ничего не надо. В постановке нашей задачи это означает, что если мы шли по цепочке отделов и дошли до сотрудника, то дальше по этой ветке искать уже незачем.
Давайте введем в нашу таблицу дополнительное
boolean-поле, которое будет нам сразу говорить, является ли эта вот конкретная запись в нашем дереве «узлом» — то есть могут ли у него вообще существовать потомки.ALTER TABLE hier
ADD COLUMN branch boolean;
UPDATE
hier T
SET
branch = TRUE
WHERE
EXISTS(
SELECT
NULL
FROM
hier
WHERE
pid = T.id
LIMIT 1
);
-- Запрос успешно выполнен: 3033 строк изменено за 42 мс.Отлично! Оказывается у нас только чуть больше 30% всех элементов дерева имеют потомков.
Теперь применим несколько иную механику — соединения с рекурсивной частью через
LATERAL, что позволит нам сразу обратиться к полям рекурсивной «таблицы», а агрегатную функцию с условием фильтрации по признаку узла используем для уменьшения набора ключей:
WITH RECURSIVE T AS (
SELECT
array_agg(id) id$
, array_agg(id) FILTER(WHERE branch) ns$
FROM
hier
WHERE
id = 5300
UNION ALL
SELECT
X.*
FROM
T
JOIN LATERAL (
SELECT
array_agg(id) id$
, array_agg(id) FILTER(WHERE branch) ns$
FROM
hier
WHERE
pid = ANY(T.ns$)
) X
ON coalesce(T.ns$, '{}') <> '{}'
)
SELECT
unnest(id$) id
FROM
T;
[посмотреть на explain.tensor.ru]
Мы смогли сократить еще одно обращение к индексу и выиграли более чем в 2 раза по объему вычитываемого.
#2. Вернемся к корням
Этот алгоритм будет полезен, если вам необходимо собрать записи для всех элементов «вверх по дереву», сохранив при этом информацию, каким исходным листом (и с какими показателями) вызвано его попадание в выборку — например, для формирования сводного отчета с агрегацией на узлы.

Дальнейшее стоит воспринимать исключительно как proof-of-concept, поскольку запрос получается очень уж громоздкий. Но если он доминирует в вашей базе — стоит задуматься над применением подобных методик.
Начнем с пары простых утверждений:
- Одну и ту же запись из базы лучше читать всего один раз.
- Записи из базы эффективнее читать «пачкой», чем поодиночке.
Теперь попробуем сконструировать нужный нам запрос.
Шаг 1
Очевидно, что на инициализации рекурсии (куда же без нее!) нам придется вычитать записи самих листьев по набору исходных идентификаторов:
WITH RECURSIVE tree AS (
SELECT
rec -- это цельная запись таблицы
, id::text chld -- это "набор" приведших сюда исходных листьев
FROM
hier rec
WHERE
id = ANY('{1,2,4,8,16,32,64,128,256,512,1024,2048,4096,8192}'::integer[])
UNION ALL
...Если кому-то показалось странным, что «набор» хранится строкой, а не массивом, то этому есть простое объяснение. Для строк существует встроенная агрегирующая «склеивающая» функция
string_agg, а для массивов — нет. Хотя ее и несложно реализовать самостоятельно.Шаг 2
Теперь нам бы получить набор ID разделов, которые надо будет вычитать дальше. Почти всегда они будут дублироваться у разных записей исходного набора — поэтому нам бы их сгруппировать, сохранив при этом информацию о листьях-источниках.
Но тут нас поджидают три неприятности:
- «Подрекурсивная» часть запроса не может содержать агрегатных функций с
GROUP BY. - Обращение к рекурсивной «таблице» не может находиться во вложенном подзапросе.
- Запрос в рекурсивной части не может содержать CTE.
К счастью, все эти проблемы достаточно легко обходятся. Начнем с конца.
CTE в рекурсивной части
Вот так не работает:
WITH RECURSIVE tree AS (
...
UNION ALL
WITH T (...)
SELECT ...
)А так — работает, скобочки решают!
WITH RECURSIVE tree AS (
...
UNION ALL
(
WITH T (...)
SELECT ...
)
)Вложенный запрос к рекурсивной «таблице»
Хм… Обращение к рекурсивной CTE не может быть во вложенном запросе. Но оно может быть внутри CTE! А вложенный запрос может обращаться уже к этой CTE!
GROUP BY внутри рекурсии
Неприятно, но… У нас же есть простой способ, как можно сэмулировать GROUP BY с помощью
DISTINCT ON и оконных функций!SELECT
(rec).pid id
, string_agg(chld::text, ',') chld
FROM
tree
WHERE
(rec).pid IS NOT NULL
GROUP BY 1 -- не работает!А вот так — работает!
SELECT DISTINCT ON((rec).pid)
(rec).pid id
, string_agg(chld::text, ',') OVER(PARTITION BY (rec).pid) chld
FROM
tree
WHERE
(rec).pid IS NOT NULLВот теперь мы видим, зачем числовой ID превращался в текст — чтобы их можно было склеивать через запятую!
Шаг 3
Для финала нам осталось всего ничего:
- вычитываем записи «разделов» по набору сгруппированных ID
- сопоставляем вычитанные разделы с «наборами» исходных листов
- «разворачиваем» строку-набор с помощью
unnest(string_to_array(chld, ',')::integer[])
WITH RECURSIVE tree AS (
SELECT
rec
, id::text chld
FROM
hier rec
WHERE
id = ANY('{1,2,4,8,16,32,64,128,256,512,1024,2048,4096,8192}'::integer[])
UNION ALL
(
WITH prnt AS (
SELECT DISTINCT ON((rec).pid)
(rec).pid id
, string_agg(chld::text, ',') OVER(PARTITION BY (rec).pid) chld
FROM
tree
WHERE
(rec).pid IS NOT NULL
)
, nodes AS (
SELECT
rec
FROM
hier rec
WHERE
id = ANY(ARRAY(
SELECT
id
FROM
prnt
))
)
SELECT
nodes.rec
, prnt.chld
FROM
prnt
JOIN
nodes
ON (nodes.rec).id = prnt.id
)
)
SELECT
unnest(string_to_array(chld, ',')::integer[]) leaf
, (rec).*
FROM
tree;
[посмотреть на explain.tensor.ru]


remzalp
А почему не рассматривались альтернативные варианты?
Например рекурсивный с костылями. При обновлении дополнительная работа, но при выборке приличное ускорение простым запросом
Kilor Автор
Это отдельная большая тема для другой статьи — в каких случаях как эффективнее «материализовывать» иерархию, как модифицировать и как выбирать потом.
force
Т.е. куча страданий и потраченного времени программиста, лишь бы не вводить Lineage или какой-нить Nested set? Которые кучу проблем смогли бы решить гораздо проще.
Kilor Автор
Возьмем классический пример прямо из wiki про Nested Set:
А теперь попробуем создать еще одну новую категорию внутри Jackets [6:7]…
Ой, надо все переупорядочивать, если ID целочисленные.
Ой, а на эти ID в иерархичном словаре что-то внешнее при этом ссылалось.
То есть если иерархия нестатична, то Nested Set не самая подходящая модель.
force
Кирилл, твой ответ выглядит так, что ты пошёл гуглить что такое Nested Set и взял первую ссылку из гугла на википедию, и из этого сделал выводы :)
Отвечаю:
1. Да, Nested сет имеет более затратные операции изменения иерархии, при этом сильно упрощая операции поиска. Если у вас постоянная текучка кадров, что операции вставки становятся неприлично тяжёлыми, то стоило бы упомянуть это в задаче. Т.к. большинство иерархий достаточно редко меняются.
2. В Nested Set надо переупорядочивать только Left/Right указатели, Id — это отдельное поле, которое трогать не надо.
Kilor Автор
Так я ровно про это и написал выше:
Если мы заранее не знаем на 100%, как часто будет меняться структура, как много будет в ней элементов и т.д., то самый простой вариант — именно через ID предка.
force
А как вы разрабатываете? Т.е. задача формулируется максимально абстрактно, и делается максимально абстрактно? Если вы настолько не знаете требования к своей же функциональности.
Через ID предка — самый простой вариант, но самый неэффективный. И оптимизировать его, вместо использования более логичных структур — интересное, но не очень полезное занятие.
Небольшую иерархию можно вообще засосать в память и не париться ни о чём. А если иерархия с 10 млн элементами, то стоит всё-таки подумать о конретных требованиях к задаче.
Конечно же, если статья написана с целью рассказать про CTE и рекурсивные джойны, а в реальности вы используете что-то другое, то это отдельный разговор.
Kilor Автор
Ну вот представьте, что вы строите иерархию адресов России — пресловутый КЛАДР. Можно быть увереным, что регионы не меняются.
Ну то есть с момента последнего такого факта прошло уже 12 лет, «точно не будет», а потом — ой…
force
Т.е. раз в 12 лет поменять строчки в базе — это гигантская проблема?
А в течение 12 лет тратить на обогрев улицы ресурсы CPU постоянно делая неэффективные операции — это норма?
Kilor Автор
Это сильно зависит от глубины легаси и частоты таких запросов.
Тут была история, как банки Cobol-специалистов искали, так что иногда и «поменять строчки» — проблема.
force
Про глубину legacy и скриншоты СБИСа мне понравилось :)
Но вообще, есть же вьюшки и триггеры в базе данных, т.е. можно изменить структуру, улучшить алгоритмы, а для legacy кода подснуть представление.
OlegAxenow
Для такого deep legacy (звучит как заголовок порно-ролика) можно сделать отдельную таблицу с иерархией «сбоку». Да, дополнительный join, зато можно гибко настроить иерархию (или даже несколько).
Если такое легаси, что даже с этим сложности — остаётся только посочувствовать…
P.S. Для Cobol есть драйвер для PostgreSQL? :)
Kilor Автор
OlegAxenow
Если в иерархию пишется чаще, чем читается — повод задуматься, а стоит ли хранить её в реляционной БД :)
Nested set не самый удобный подход с точки зрения вставки, но не всё так плохо — id там менять не надо.
Kilor Автор
— PM: У нас иерархия будет 100% статична, ничего там меняться не будет!
— TL: Давайте Nested Set, а заодно сэкономим поля и объединим ID/left.
…
— PM: А давайте теперь дадим пользователю настраивать иерархию самому!
:)
OlegAxenow
Так а в чём проблема с редактированием nested set? Главное, как я уже говорил, чтобы не требовалось оптимизировать больше вставку чем чтение. А это крайне редко требуется.
Строго говоря, я вижу два варианта:
— мы со страшной силой пишем что-то, например, с датчиков и непременно в иерархию (повод задуматься о специализированном хранилище);
— требуется выпрямить руки программистам, которые небрежно спроектировали решение.
В остальных случаях, nested set будет работать нормально. Для более экзотических случаев (или экзотических разработчиков, которым вдруг сложно будет с ним разобраться) можно что-то ещё придумать.
Если интересно — зайдите на redmine.org — там вполне себе иерархические задачи на nested set и (ой!) они редактируются ;)
P.S. Может, это вообще всё сильно субъективно, но лично я между CTE со склейкой id на простой структуре БД и nested set с нетривиальной логикой по вставке выберу nested set.
Kilor Автор
Так проблем нет, надо просто стараться выбирать подходящий инструмент под известные ограничения задачи. В статье рассмотрен исключительно «один из» и как с ним работать эффективнее, если он уже есть.
OlegAxenow
IMHO — «ParentId» почти никуда не подходит, если это не приложение уровня Hello World или иерархию не «раз в год» выводят.
А nested set — он клёвый, там ещё и порядок детей задаётся «из коробки».
P.S. Вообще, далеко ушла дискуссия в статье, начинающейся со слов «PostgreSQL Antipatterns» :)