Сегодня появляется все больше 3D датасетов и задач, связанных с 3D данными. Это связано с развитием робототехники и машинного зрения, технологий виртуальной и дополненной реальности, технологий медицинского и промышленного сканирования. Алгоритмы машинного обучения помогают решать сложные задачи, в которых необходимо классифицировать трехмерные объекты, восстанавливать недостающую информацию о таких объектах, или же порождать новые. Несмотря на достигнутые успехи, в области 3D ML остаются еще нерешенными ряд задач, и эта серия заметок призвана популяризировать направление среди русскоязычного сообщества.

В первой части будут рассмотрены основные формы и форматы представления пространственных данных и их особенности.

Прежде чем вдаваться в подробности того, как именно устроены данные с которыми мы будем в дальнейшем работать, хотелось бы кратко обсудить мотивацию изучения трехмерных данных с помощью методов машинного обучения.

Заметка от партнера IT-центра МАИ и организатора магистерской программы “VR/AR & AI” — компании PHYGITALISM.

Введение

Слабый искусственный интеллект, по определению [1] призван имитировать частные сенсорные и когнитивные функции человеческого или иного разума. Одним из важнейших сенсорных навыков живых организмов является пространственное восприятие окружающего мира. Для того, чтобы ориентироваться в пространстве, живые организмы используют информацию самого разного свойства:

• Можно использовать звук для определения направления на источник, для этого у человека есть бинауральный слух, мозг улавливает временную задержку между приемом одного и того же звука от разных ушей и делает предсказание дальности и направления на источник.

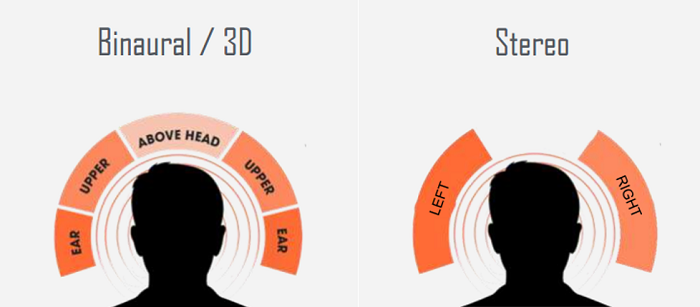
• Можно ориентироваться по гравитационному вектору, чтобы отделять понятие “низ” и “верх”. Осязание, помогает прочувствовать детали изучаемых объектов которые не видны зрению, определить негеометрические качества объекта, такие как температура.

  
  

• Но всё же одним из главных источников информации и пространстве для нас является визуальная информация. Человек обладает бинокулярным зрением, так же называемым стереоскопическим. По аналогии с бинауральным слухом, стереоскопическое зрение основано на использовании двух приёмников визуальной информации, наших глаз, для того, чтобы определять расстояние до видимых объектов.

  
  

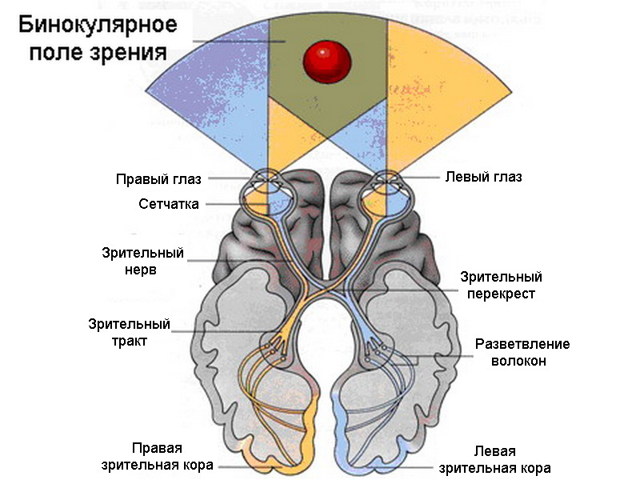
Человек может решать куда более сложную задачу, чем определение расстояния до различных объектов. По одному взгляду на объект, человек может предсказать как этот объект выглядит со всех сторон, сколько приблизительно весит этот объект, мокрый он или сухой и многие другие свойства. Используя минимум информации, мы можем делать много разнообразных выводов о том что видим перед собою. Более того, мы можем с помощью фантазии и знаний об окружающем мире моделировать различные ситуации с объектом, который наблюдаем. Например, если мы выбираем мебель в магазине, мы можем представить как она будет выглядеть в интерьере нашего дома, пройдет она в дверь подъезда или нет.

Задачи, подобные описанным выше, сегодня требуется решать не только человеку, но и технике. Аналогично тому, как бинокулярное зрение помогает нам определять расстояния до объектов, специальные глубинные камеры или RGB-D сенсоры, такие как Intel Realsense или Microsoft Azure Kinect, способны получать поток RGB-D изображений [обычное цветное (RGB изображение + карта глубины (depth map)], Как работают камеры глубины, и как можно использовать их для решения задачи сканирования помещений, можно прочитать в нашей статье. Аппараты МРТ способны восстанавливать трехмерную карту плотности тканей живых организмов по множествам двумерных срезов, аналогично тому как человек может представлять себе форму объекта, который он осмотрел с разных сторон и в разных разрезах.

Существует ряд практических задач, в которых требуется определять структуру пространства:

• сканирование помещений для воссоздания их копий на компьютере,
• навигация беспилотных дронов и автомобилей,
• корректное позиционирование объектов в дополненной реальности,
• генерация новых трехмерных моделей,
• анализ медецинских сканов мягких тканей,
• поиск уязвимых мест в строительных конструкциях.

Однако, для решения этих задач силами человека-специалиста, требуется затратить много времени и сил. Возникает вопрос: можно ли решать подобные задачи, располагая меньшим количеством данных и технических средств? Так, к примеру, можно ли не используя камеру глубины, по одному лишь RGB снимку предсказать пространственную структуру объекта, изображенного на данном снимке?

Сегодня для решения данного вопроса всё чаще прибегают к методам машинного обучения. Если представлять работту алгоритма машинного обучения в виде “чёрного ящика” (black box), которому на вход подаются данные заданного типа и на выходе алгоритм выдает предсказание в форме данных заданного типа, то в случае, если на входе и/или выходе представлены данные, кодирующие трехмерные структуры, говорят об области машинного обучения, которая называется 3D ML (three dimensional data machine learning problems) или, часто встречается термин Geometrical deep learning, если речь идет о применении глубоких архитектур.

Типы задач, которые необходимо решать в области 3D ML могут быть самыми разными:

• классические задачи (классификации и кластеризации 3D данных),
• генерация 3D контента (порождающие модели)
• восстановление 3D модели объекта по одному или нескольким RGB изображениям этого объекта (2D-to-3D),

• анимирование статичного меша и многие другие.

  
  

  

  
  Рис.1 3D ML IDF0 scheme.
  

В последнее время большую популярность в области 3D ML получили методы глубокого обучения. Это можно объяснить тем, что для работы большинства классических алгоритмов машинного обучения необходимы аналитические функции для манипулирования над данными. Например, для того чтобы построить метрические алгоритмы классификации / кластеризации, нужно ввести метрику в пространстве 3D моделей. Такие метрики можно конструировать с помощью трехмерных дескрипторов Цернике [2] — спектрального разложение двумерных многообразий, аналог преобразования Фурье (мы написали заметку про применению таких дескрипторов в задачи поиска среди 3D моделей).

Так, например, авторы в работе “Characterizing Structural Relationships in Scenes Using Graph Kernels” [3] используют трехмерные дескрипторы Зернике для построения метрического ядра для кластеризации сложных трехмерных сцен, а в “Fast human pose estimation using 3D Zernike descriptors” [4] авторы используют дескрипторы для построение быстрой и устойчивой модели оценки человеческой позы в пространстве. Но для большинства задач 3D ML, подобрать подобные функцией оказывается большим испытанием. В этом случае использование нейронных сетей является более понятной и простой альтернативой.

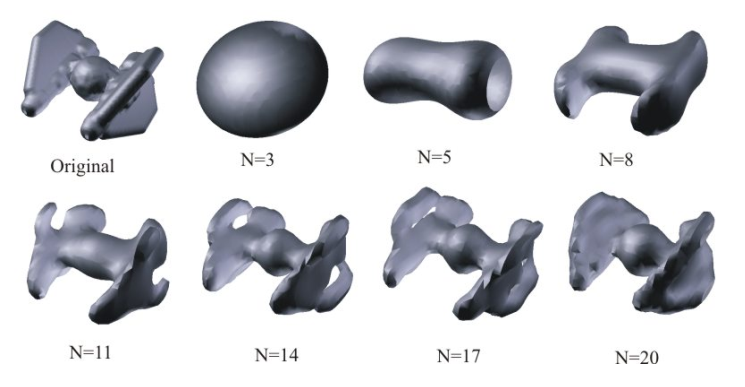
Рис.2 Слева сверху — оригинальная вокселизованная 3D модель космического корабля. Остальные изображения — меш, восстановленный из изоповерхностей, описываемых дескрипторами Цернике. Число N обозначает количество различных моментов Цернике, использованных для восстановления. Иллюстрация из статьи [2].

На сегодняшний день существует уже множество различных архитектур глубокого обучения для решения задач в области 3D ML, но все их можно условно разделить на несколько видов, в зависимости от типа задачи и типа данных. В данной заметке мы рассмотрим только одну задачу 3D ML, а именно задачу single image 2D-to-3D, чья формальная постановка будет описана в следующей заметке.
Но перед тем как разбираться с постановкой задачи, нужно описать существующие наиболее распространенные способы представления 3D данных и их особенности.

Формы представления 3D данных

Данные — одна из важнейших составляющих машинного обучения. Чем их больше, тем лучше мы сможем обучить нашу модель, тем больше у неё будет обобщающая способность. И действительно, ниже мы будем говорить об алгоритмах машинного обучения и о том, как они работают с данными, но ведь прежде всего эти данные нужно извлечь из внешнего мира и подготовить для обработки. В реальных задачах препроцессинг данных и оптимизация пайплайна обработки данных занимает большую часть времени.

Важной деталью при непосредственном выборе модели машинного обучения, которая будет решать поставленную задачу, является выбор формы представления данных. Для одних и тех же данных их представления могут сильно отличаться, что и повлияет на выбор модели обработки. Так, например, обычный текст мы можем представить как линейную последовательность символов и в этом случае для обработки данных лучше подойдут рекуррентные архитектуры, а в случае, если текст представлен как изображение, то для обработки данных лучше подойдут сверточные архитектуры.

Какой именно формой данных нужно пользоваться при решении конкретной задачи определяется тем, какие данные уже доступны на данный момент, тем каким образом данные извлекаются из внешнего мира и тем, какой аспект данных наиболее приоритетен в конкретной задаче.

Если говорить об области обработки изображений, то существует канонический способ представления информации в виде растровых RGB изображений, т.е. по сути мы храним три числовых матрицы. Иногда к трем основным каналам могут добавиться ещё несколько, например изображения со спутников могут иметь ещё инфракрасный канал, ультрафиолетовый и т.д. Такой способ представления данных является одновременно и вычислительно эффективным, потому что для работы с матрицами и их многомерными аналогами — тензорами существует множество готовых быстрых алгоритмов обработки, которые к тому же хорошо перекладываются на вычисления на видеокартах.

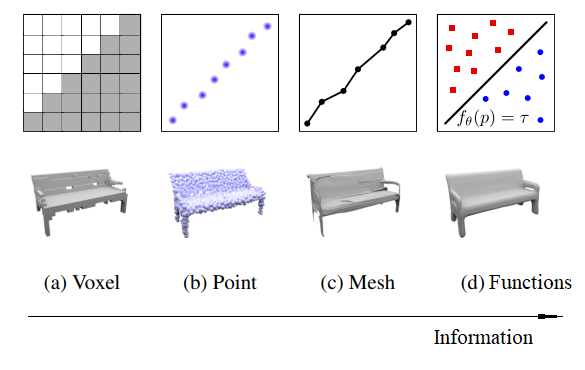
Рис.3 Сравнение форм представления 3D данных: основные 4 типа в порядке возрастания пространственной информативности, их 2D аналоги. Иллюстрация из статьи [5].

Для области же 3D ML, на сегодняшний день нет единой формы представления данных, которая была бы одновременно компакта, вычислительно эффективна и легко извлекалась из реальных данных.

Далее будет рассматривать примеры работы с данными на Python, используя наиболее популярные фреймворки для работы с 3D:

• trimesh
• pytorch3d

Примеры кода и данные для тестов можно найти в репозитории на GitHub.

Для начала, загрузим все необходимые для работы библиотеки и, если есть такая возможность, установим в качестве устройства для обработки тензоров pytorch CUDA совместимую видеокарту.

import os
os.environ['PYOPENGL_PLATFORM'] = 'egl'
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline

import torch

# untilitis 
from pytorch3d.utils import ico_sphere

# loss functions and regulaziers
from pytorch3d.loss import (
    chamfer_distance,
    mesh_edge_loss,
    mesh_laplacian_smoothing,
    mesh_normal_consistency
)

# io utils
from pytorch3d.io import load_obj

# operations with data
from pytorch3d.ops import sample_points_from_meshes

# datastructures
from pytorch3d.structures import Meshes, Textures

# render 
from pytorch3d.renderer import (
    look_at_view_transform,
    OpenGLPerspectiveCameras,
    DirectionalLights, 
    RasterizationSettings, 
    MeshRenderer, 
    MeshRasterizer,  
    HardPhongShader
)

# mesh_to_sdf lib by marian42
from mesh_to_sdf import mesh_to_sdf, sample_sdf_near_surface

# trimesh lib imports
import trimesh
from trimesh.voxel.creation import voxelize

# If you have got a CUDA device, you can use GPU mode
if torch.cuda.is_available():
  device = torch.device('cuda:0')
  torch.cuda.set_device(device)
else:
  device = torch.device('cpu')

Чаще всего, например как в работе [5], выделяют четыре основных способа представления трехмерных данных.

Полигональные модели (Mesh, polygonal models)

Полигональные модели — традиционная форма представления трехмерных данных в компьютерной графике. Существует ряд форматов для работы с полигональными моделями, например это форматы FBX, glTF, glb. Однако одним из основных является .obj формат. Физически такие модели представляют из себя пространственный граф, т.е. могут храниться в памяти компьютера в виде двух множеств: множество вершин и множество ребер, соединяющих вершины, хотя чаще используются вершины и тройки вершин, образующие элементарные полигоны.

Полигональная модель в формате .obj в одном из способов своего представления является ASCII файлом (в другом варианте .obj модель может быть записана в бинарный файл), в котором записаны координаты вершин, индексы вершин, составляющие полигоны, а также текстуры, нормали и пр.

# OBJ file format with ext .obj
# vertex count = 2503
# face count = 4968
v -3.4101800e-003 1.3031957e-001 2.1754370e-002
v -8.1719160e-002 1.5250145e-001 2.9656090e-002
v -3.0543480e-002 1.2477885e-001 1.0983400e-003
v -2.4901590e-002 1.1211138e-001 3.7560240e-002
...
f 1069 1647 1578
f 1058 909 939
f 421 1176 238
f 1055 1101 1042
f 238 1059 1126
f 1254 30 1261
f 1065 1071 1
f 1037 1130 1120
f 1570 2381 1585
f 2434 2502 2473
f 1632 1654 1646
...

К преимуществам полигональных моделей можно отнести:

• Естественный формат для использования в компьютерной графике, игровых движках и т.д.
• Позволяет лучше описывать пространственные особенности объектов (топология, форма поверхности), по сравнению с воксельными моделями низкого разрешения или с облаками точек.

К недостаткам полигональных моделей можно отнести:

• Необходимость создания специального математического аппарата для извлечения признаков из полигональных моделей, например, свертки на графах.
• Чувствительность формата к выбросам в данных.

Во всех своих phygital-проектах мы используем именно эту форму представления трехмерных данных, так как она является стандартом для игровых движков, таких как Unity 3D.

В качестве тестовой модели будем использовать знаменитого стэнфордского кролика, а также создадим икосферу, которая присутствует в наборе базовых трехмерных примитивов в большинстве пакетов для работы с 3D.

Создание полигональной икосферы sphere.obj с 4 уровнями subdivision:

# Trimesh sphere .obj model
trimesh_sphere = trimesh.primitives.Sphere(subdivisions= 4)

# Sphere mesh in pytorch3d
sphere_mesh = ico_sphere(4, device)

verts_rgb = torch.ones_like(sphere_mesh.verts_list()[0])[None]

# Rainbow sphere in pytorch3d
# verts_rgb = torch.rand_like(sphere_mesh.verts_list()[0])[None]

sphere_mesh.textures = Textures(verts_rgb=verts_rgb.to(device))

Создание полигональной модели кролика bunny.obj:

path_to_model = os.path.join("/data","bunny.obj")

# Trimesh bunny .obj model
bunny_trimesh = trimesh.load(path_to_model)

if isinstance(bunny_trimesh, trimesh.Scene):
    bunny_trimesh = bunny_trimesh.dump(concatenate=True)

bunny_trimesh.vertices -= bunny_trimesh.center_mass
scaling = 2 / bunny_trimesh.scale
bunny_trimesh.apply_scale(scaling=scaling)

# Rainbow bunny in trimesh
# for facet in bunny_trimesh.facets:
#   bunny_trimesh.visual.face_colors[facet] = trimesh.visual.random_color() 

# Bunny mesh in pytorch3d
verts, faces_idx, _ = load_obj(path_to_model)
faces = faces_idx.verts_idx

center = verts.mean(0)
verts = verts - center
scale = max(verts.abs().max(0)[0])
verts = verts / scale

# Initialize each vertex to be white in color.
verts_rgb = torch.ones_like(verts)[None]  # (1, V, 3)

# Rainbow bunny in pytorch3d
# verts_rgb = torch.rand_like(verts)[None]

textures = Textures(verts_rgb=verts_rgb.to(device))

# Create a Meshes object for the bunny.
bunny_mesh = Meshes(
    verts=[verts.to(device)],   
    faces=[faces.to(device)], 
    textures=textures
)

Для визуализации моделей и работы с изображениями часто используют специальный модуль — дифференциальный рендерер, который содержит в себе модели освещения, шейдеры, расторизаторы и многие другие модули, характерные для компьютерной графики.

Подготовка дифференциального рендерера сцены:

# Initialize an OpenGL perspective camera.
cameras = OpenGLPerspectiveCameras(device=device)

# We will also create a phong renderer. This is simpler and only needs to render one face per pixel.
raster_settings = RasterizationSettings(
    image_size=1024, 
    blur_radius=0, 
    faces_per_pixel=1, 
)

# We can add a point light in front of the object. 
#lights = PointLights(device=device, location=((2.0, 2.0, -2.0),))
ambient_color = torch.FloatTensor([[0.0, 0.0, 0.0]]).to(device)
diffuse_color = torch.FloatTensor([[1.0, 1.0, 1.0]]).to(device)
specular_color = torch.FloatTensor([[0.1, 0.1, 0.1]]).to(device)
direction = torch.FloatTensor([[1, 1, 1]]).to(device)
lights = DirectionalLights(ambient_color=ambient_color,
                           diffuse_color=diffuse_color,
                           specular_color=specular_color,
                           direction=direction,
                           device=device)

phong_renderer = MeshRenderer(
    rasterizer=MeshRasterizer(
        cameras=cameras, 
        raster_settings=raster_settings
    ),
    shader=HardPhongShader(
        device=device, 
        cameras=cameras, 
        lights=lights
        )
)

Рендеринг наших моделей:

Кролик

# Select the viewpoint using spherical angles  
distance = 2.0   # distance from camera to the object`
elevation = 40.0   # angle of elevation in degrees
azimuth = 0.0  # No rotation so the camera is positioned on the +Z axis. 

# Get the position of the camera based on the spherical angles
R, T = look_at_view_transform(distance, elevation, azimuth, device=device,at=((-0.02,0.1,0.0),))

# Render the bunny providing the values of R and T. 
image_bunny = phong_renderer(meshes_world=bunny_mesh, R=R, T=T)

image_bunny = image_bunny.cpu().numpy()

plt.figure(figsize=(13, 13))
plt.imshow(image_bunny.squeeze())
plt.grid(False)

Икосфера

# Select the viewpoint using spherical angles  
distance = 3.0   # distance from camera to the object`
elevation = 40.0   # angle of elevation in degrees
azimuth = 0.0  # No rotation so the camera is positioned on the +Z axis. 

# Get the position of the camera based on the spherical angles
R, T = look_at_view_transform(distance, elevation, azimuth, device=device,at=((-0.02,0.1,0.0),))

# Render the sphere providing the values of R and T. 
image_sphere = phong_renderer(meshes_world=sphere_mesh, R=R, T=T)

image_sphere = image_sphere.cpu().numpy()

plt.figure(figsize=(13, 13))
plt.imshow(image_sphere.squeeze())
plt.grid(False)

Красиво отрендеренная модель это прекрасно, но зачастую, для того, чтобы лучше понять с какими данными мы работаем, необходимо интерактивно взаимодействовать с ней (вращать и масштабировать, выделять составные части и многое другое). Такую возможность предоставляет библиотека trimesh с ее интерактивной визуализацией:

bunny_trimesh.show()

Поскольку полигональная модель представляет из себя по своей математической природе пространственный граф, состоящий из набора вершин и ребер, соединяющих эти вершины, то можно задаться вопросом вычисления характеристик, свойственных для такой формы представления. Например, это может быть Эйлерова характеристика пространственного графа, характеристика поверхностного натяжения меша (watertight mesh) или же его объем, или точка центра масс.

print(
    "Эйлерова характеристика пространственного графа модели bunny Xi = V - E + F =",
    bunny_trimesh.euler_number
)

print(
    "Эйлерова характеристика пространственного графа модели sphere Xi = V - E + F =",
    trimesh_sphere.euler_number
)

print("Is bunny mesh watertight:", bunny_trimesh.is_watertight)
print("Is sphere mesh watertight:", trimesh_sphere.is_watertight)

print("Объем модели bunny.obj:", bunny_trimesh.volume)
print("Объем модели sphere.obj:", trimesh_sphere.volume)

# Объем единичной сферы 4/3 * Pi
(4/3)*np.pi

Out:

>>Эйлерова характеристика пространственного графа модели bunny Xi = V - E + F = -2
>>Эйлерова характеристика пространственного графа модели sphere Xi = V - E + F = 2
>>Is bunny mesh watertight: False
>>Is sphere mesh watertight: True
>>Объем модели bunny.obj: 0.3876657353353089
>>Объем модели sphere.obj: 4.1887902047863905
>>4.1887902047863905

Воксели (Voxels)

Воксели (от англ. слов volumetric + pixel) являются обобщением пикселей на пространственный случай. Воксельные 3D модели представляют из себя кубические пространственные сетки, в которых объекты представляются множеством маленьких кубиков (вокселей). В компьютере воксели хранятся в виде трехмерной матрицы. Существует ряд форматов, для хранения воксельных моделей, но наиболее распространённым, видимо, является .vox формат. Помимо применения в играх и компьютерной графике в качестве необычного графического стиля (т.н. pixel and voxel art), воксельное представления трехмерных данных часто встречается в медицине и промышленном производстве.

В медицине эта форма данных возникает при работе с томографическими данными, оказывается что среднее значение плотности тканей удобно рассчитывать именно на кубической сетке, а в промышленности, моделирование взаимодействия ЧПУ станка с твердым материалом удобно представлять с помощью булевых операций над двумя множествами, ведь в самом деле, в отличие от полигональных моделей, у воксельных моделей внутреннее пространство не заполнено пустотой, а значит сдвигая или уничтожая отдельные воксели модели, можно моделировать процессы разрушения или деформации твёрдого тела. В самом простом варианте реализации, воксельная модель представляет из себя трехмерный массив, заполненный нулями и единицами (1 — в данной точке пространственной сетке есть воксель, 0 — нет вокселя).

Для вокселизации имеющийся у нас модели воспользуемся встроенным вокселезатором из trimesh:

low_idx_bunny = bunny_trimesh.scale / 15
high_idx_bunny = bunny_trimesh.scale / 39
low_idx_sphere = trimesh_sphere.scale / 15
high_idx_sphere = trimesh_sphere.scale / 30
vox_high_bunny = voxelize(bunny_trimesh,pitch=high_idx_bunny)
vox_high_sphere = voxelize(trimesh_sphere,pitch=high_idx_sphere)
print("Размер воксельной сетки с высоким разрешением:", vox_high_sphere.shape)
print("Размер воксельной сетки с низким разрешением:", vox_low_sphere.shape)
print("Срез воксельной сетки:\n",np.array(vox_high_sphere.matrix, dtype=np.uint8)[1])

Out:

>>Размер воксельной сетки с низким разрешением: (9, 9, 9)
>>Размер воксельной сетки с высоким разрешением: (19, 19, 19)
>>Срез воксельной сетки:
array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]],
      dtype=uint8)

К преимуществам воксельного подхода можно отнести:

• Естественное обобщение подходов, которые применялись для обработки изображений, например трехмерная свертка.
• Данные для обучения легко получить из любого другого типа моделей.
• Большая связь с физическими свойствами объектов по сравнению с полигональными и облачными моделями.
• Возможность представлять воксельные модели в виде обычных векторов.

К недостаткам воксельного подхода можно отнести:

• “Грубость” аппроксимации формы реальных объектов при малом разрешении.
• Объём занимаемой воксельными моделями памяти растёт кубически в зависимости от количество интервалов, на которое разбивается каждая ось.

Для того, чтобы визуально оценить качество вокселизации модели в trimesh имеется встроенный интерактивный визуализатор:

vox_high_sphere.show()
vox_low_sphere.show()

С одной стороны, воксельный подход является на сегодняшний день наиболее распространённым из-за простоты его описания, также из-за корпускулярности данная форма наиболее приспособлена для физических симуляций разрушаемых объектов, с другой стороны, данный подход ограничен низким разрешением пространственной сетки. Типичным диапазоном разрешений воксельной сетки является диапазон от $$ до $$. Несмотря на то, что исследователи пытаются решить проблему низкой размерности, так, например, в [6] авторы использовали октодеревья для построения архитектуры глубокого обучения OGN (Octree Generating Networks), которая позволила работать с сеткой более высокого разрешение чем в предшествующих работах, у данного подхода есть ещё ряд других нерешенных проблем.

Облака точек (Point clouds)

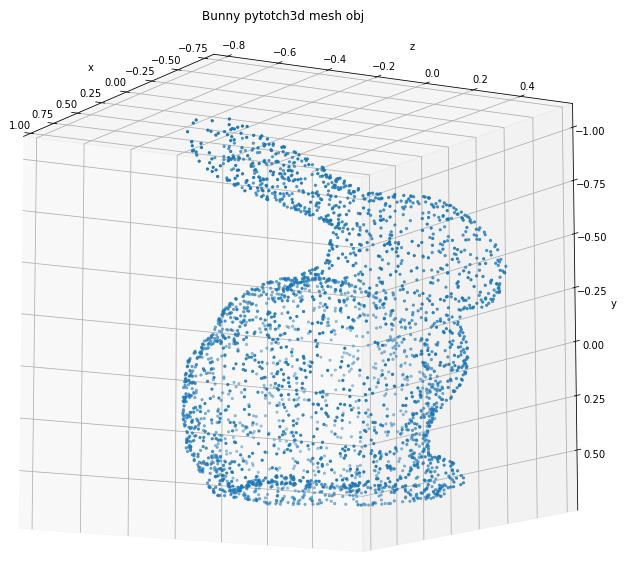
Облако точек является типичной формой данных о пространстве в робототехнике и компьютерном зрении. Физически облако точек представляет собой неупорядоченное множество трехмерных радиус-векторов. Иногда для каждого такого вектора (точки) можно дополнительно указать ее цвет, как дополнительное составляющей не влияющее на геометрию. Такая форма представления пространственных данных часто на практике встречается в задачах сканирования помещений или отдельно взятых объектов. Камеры глубины в качестве результата работы возвращают изображение вместе с его картой глубины (RGBD), что является частным случаем облака точек. Восстановления карты глубины для данного изображения часто называют задачами 2.5D, указывая на то, что, снятый глубинной камерой объект с одного ракурса, не может быть дополнен пространственной информацией с другого ракурса. В этом смысле облако точек содержит в себе больше информации о геометрии объектов чем RGBD изображения.

Примером формата, с помощью которого хранят облака точек является .pcd формат, хотя чаще сканы в виде облака точек хранят в .ply формате. Также стоит отметить, что существует очень удобная, оптимизированная и разнообразная библиотека для обработки данных данного формата — PCL.

Рассматриваемую нами модель кролика в форме облака точек в формате .ply можно найти на официальном сайте стэнфорда:

ply
format ascii 1.0
obj_info is_cyberware_data 1
obj_info is_mesh 0
obj_info is_warped 0
obj_info is_interlaced 1
obj_info num_cols 512
obj_info num_rows 400
obj_info echo_rgb_offset_x 0.013000
obj_info echo_rgb_offset_y 0.153600
obj_info echo_rgb_offset_z 0.172000
obj_info echo_rgb_frontfocus 0.930000
obj_info echo_rgb_backfocus 0.012660
obj_info echo_rgb_pixelsize 0.000010
obj_info echo_rgb_centerpixel 232
obj_info echo_frames 512
obj_info echo_lgincr 0.000500
element vertex 40256
property float x
property float y
property float z
element range_grid 204800
property list uchar int vertex_indices
end_header
-0.06325 0.0359793 0.0420873 
-0.06275 0.0360343 0.0425949 
-0.0645 0.0365101 0.0404362 
-0.064 0.0366195 0.0414512 
-0.0635 0.0367289 0.0424662 
-0.063 0.0367836 0.0429737 
-0.0625 0.0368247 0.0433543 
-0.062 0.0368657 0.0437349 
-0.0615 0.0369067 0.0441155 
-0.061 0.0369614 0.044623 
...

К преимуществам облака точек можно отнести:

• Естественный формат данных в задачах пространственного сканирования.
• Данные данного формата могут быть легко получены из полигональных и функциональных моделей.

К недостаткам облака точек можно отнести:

• Неупорядоченность данных приводит к проблеме выбора функции ошибки и необходимости разработки специального математического аппарата.
• Отсутствует информация о связях между точками, что не позволяет корректно восстановить геометрию и топологию исследуемого объекта и требует сложной процедуры постпроцессинга для перевода результата в иные формы представления пространственных данных.

Для того, чтобы работать с облаком точек, можно загрузить .ply модель и создать объект класса PointClud, а можно получить облако точек из текущей .obj модели. Для того, чтобы облако точек, полученное из полигональной модели, было достаточно информативным, необходимо, чтобы точки из которых оно состоит достаточно равномерно и полно покрывали поверхность объекта. Для этого существуют специальные методы сэмплирования точек на поверхности.

Мы можем воспользоваться методом, встроенным в pytorch3d, тем более что он позволяет помимо самих координат точек генерировать и нормали для них:

# Mesh to pointcloud with normals in pytorch3d
num_points_to_sample = 25000

bunny_vert, bunny_norm = sample_points_from_meshes(
    bunny_mesh,
    num_points_to_sample ,
    return_normals=True
)

sphere_vert, sphere_norm = sample_points_from_meshes(
    sphere_mesh,
    num_points_to_sample,
    return_normals=True
)

Визуализируем заданное облакоточек функцией:

def plot_pointcloud(points, elev=70, azim=-70, title=""):
    # Sample points uniformly from the surface of the mesh.
    fig = plt.figure(figsize=(10, 10))
    ax = Axes3D(fig)
    x, y, z = points
    ax.scatter3D(x, z, -y,marker='.')  
    ax.set_xlabel('x')
    ax.set_ylabel('z')
    ax.set_zlabel('y')
    ax.set_title(title)
    ax.view_init(elev, azim)
    plt.show()

Посмотрим на результат визуализации облаков точек для наших моделей (pytorch3d):

points = sample_points_from_meshes(bunny_mesh, 5000)
points = points.clone().detach().cpu().squeeze().unbind(1)
plot_pointcloud(points, elev=190, azim=150, title='Bunny pytotch3d mesh obj')

points = sample_points_from_meshes(sphere_mesh, 3000)
points = points.clone().detach().cpu().squeeze().unbind(1)
plot_pointcloud(points, elev=190, azim=130, title='Sphere pytotch3d mesh obj')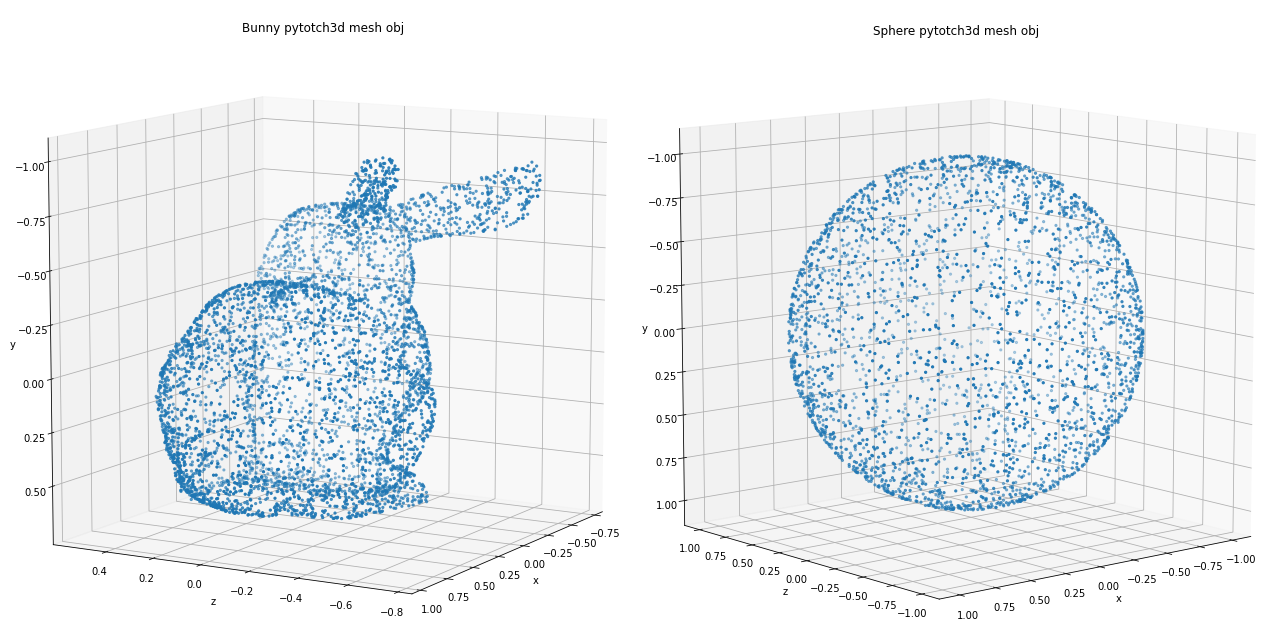

Проблема неупорядоченности данных (повернув или отмасштабировав 3D модель, данные её описывающее существенно меняются, при этом по сути модель остаётся прежней) характерна и для полигональных моделей, несмотря на это, облако точек самая редко используемая форма данных в области 3D ML. Если говорить о задаче 2D-to-3D, то изображение в данный формат вообще не принято переводить, вместо этого решают другую задачу PC2Mesh (восстановление полигональной модели из облака точек).

Твердотельные/функциональные модели (CAD models, functions)

Основной идеей функционального подхода (т. н. твердотельные модели) является использование функционального описания поверхностей и функциональное описание физических свойств объектов. Например, помимо формы объекта, заданной некоторой функцией, можно хранить распределение массовой плотности, и тем самым иметь возможность не только корректно визуализировать объект на всех масштабах, но использовать эту же модель для расчета физических свойств. Для создания и работы с твердотельными моделями существуют специальные системы автоматического проектирования и моделирования (САПР), также в английском эквиваленты CAD и CAM системы. Форматов твердотельных моделей сегодня существует намного больше, чем любых других форматов хранения трехмерных данных. Это связано с тем, что для различных инженерных приложений, существуют различные CAD системы и у каждой присутствует свой специфический формат данных.

Функция, с помощью которой описывается геометрия объекта, может иметь разный смысл: с одной стороны это может быть аналитическое описание поверхности, которая ограничивает твёрдое тело в пространстве, с другой стороны, это может быть некоторая специфическая функция, например плотность вероятности случайной величины, которая должна с наибольшей вероятностью принадлежать внутренности объекта (пример из [5]).
Одним из наиболее распространенных способов функционального описания в 3D ML является т.н. signed distance function (SDF) — функция, которая каждой точке в пространстве ставит в соответствие расстояние до ближайшей точки поверхности объекта. Формально можно записать ее следующим образом.

Пусть рассматриваемый нами 3D объект представляется из себя подмножество $$ некоторого метрического пространства $$, т.е. $$, а поверхность нашей модели — граница этого множества, обозначаемая $$.

В данном случае, расстояние от точки до границы множества вычисляется по формуле:

Тогда сама поверхность является множеством решений уравнения: $$. Например, такой подход использован в модели DeepSDF [10]. Авторы этой же работы реализовали библиотеку mesh_to_sdf, которая позволяет вычислять значение SDF функции в окрестности произвольной 3D модели.

Рассмотрим пример вычисления SDF функции для внутренних и внешних точек рассматриваемых нами моделей:

Кролик

center_mass = bunny_trimesh.center_mass
query_points = np.array([[center_mass],[[3,3,3]]])
for point in query_points:
    print(
        "SDF{0} = {1}".format(point[0],mesh_to_sdf(bunny_trimesh,point)[0])
)

Out:

>>SDF[-0.00036814  0.01044934 -0.00012521] = -0.26781705021858215
>>SDF[3. 3. 3.] = 4.746691703796387

Икосфера

center_mass = trimesh_sphere.center_mass
query_points = np.array([[center_mass],[[3,3,3]]])
for point in query_points:
    print(
        "SDF{0} = {1}".format(point[0],mesh_to_sdf(trimesh_sphere,point)[0])
)

Out:

>>SDF[ 0.0000000e+00  0.0000000e+00 -8.8540061e-18] = -0.9988667964935303
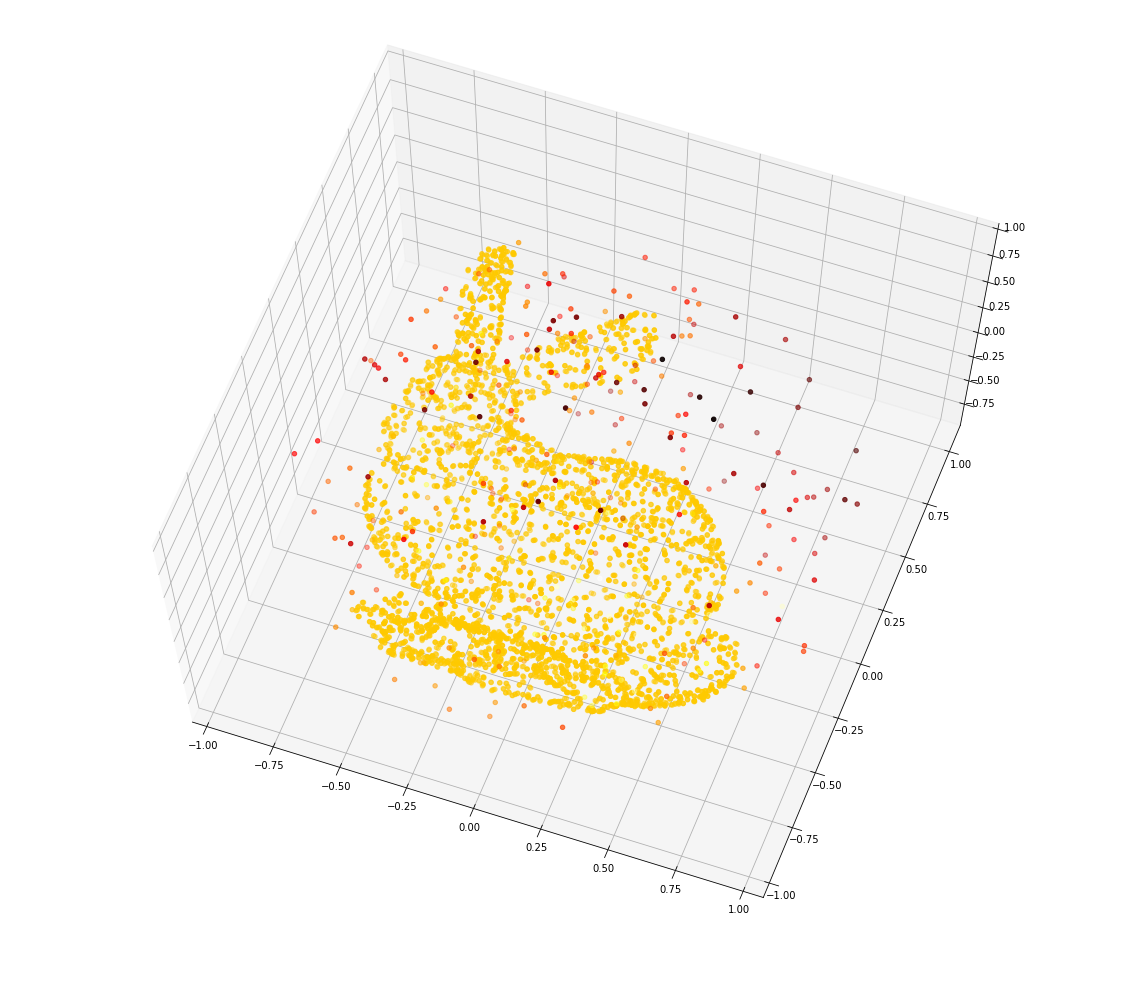
>>SDF[3. 3. 3.] = 4.195330619812012

Визуализируем SDF, просемплировав точки в окрестности моделей и разукрасив их в градиент значение функции:

points, sdf = sample_sdf_near_surface(trimesh_sphere, number_of_points=5000)
fig = plt.figure(figsize=(20, 18))
ax = fig.add_subplot(111, projection="3d")
ax.view_init(elev=70, azim=-70)
ax.scatter(points[:, 0], points[:, 1], zs=-points[:, 2], c=sdf, cmap="hot_r")

points, sdf = sample_sdf_near_surface(bunny_trimesh, number_of_points=5000)
fig = plt.figure(figsize=(20, 18))
ax = fig.add_subplot(111, projection="3d")
ax.view_init(elev=70, azim=-70)
ax.scatter(points[:, 0], points[:, 1], zs=-points[:, 2], c=sdf, cmap="hot_r")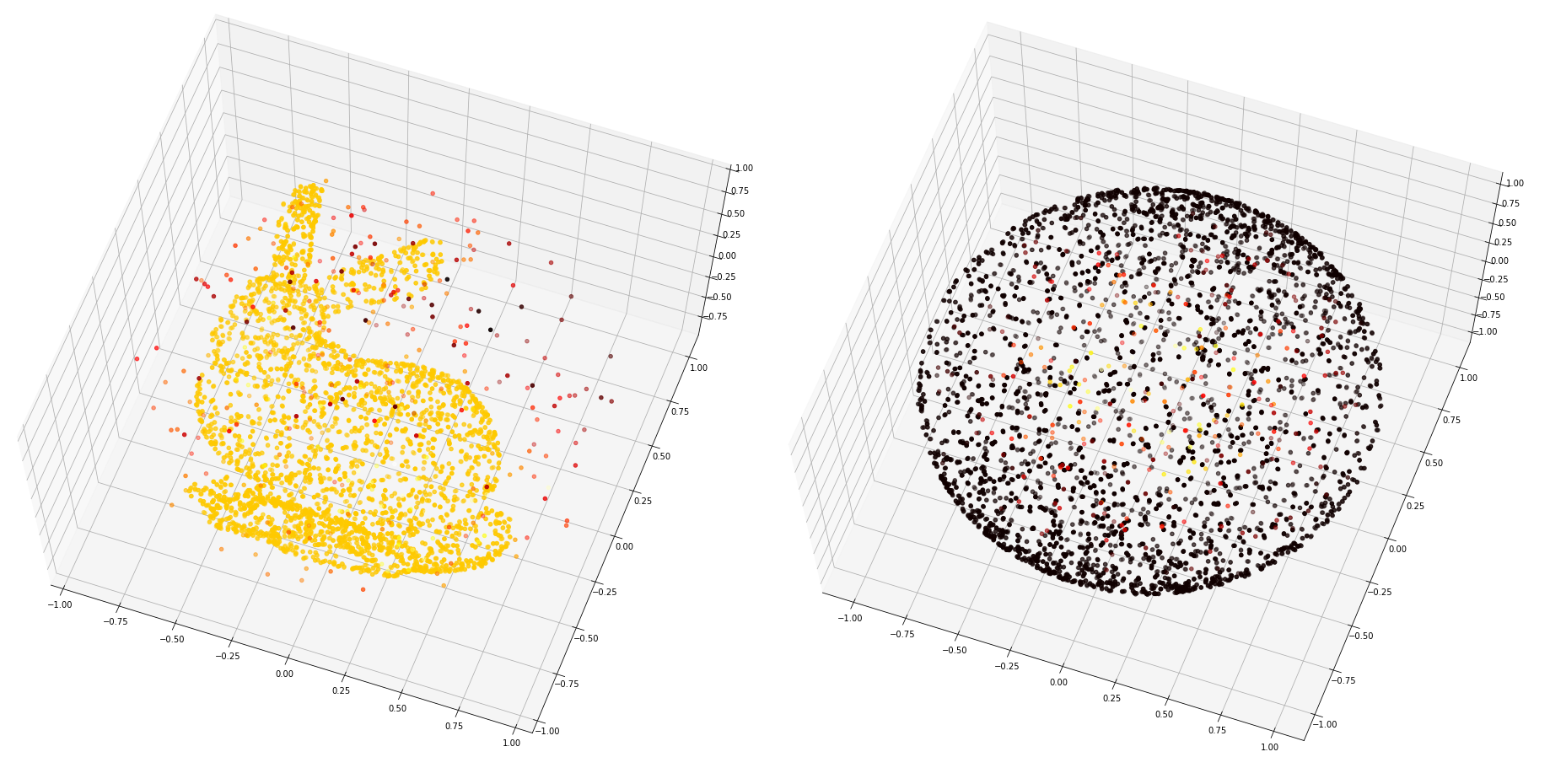

Стоит заметить, что с помощью SDF функции можно решать множество сложных и актуальных задач в области компьютерной графики и машинного обучения.

С помощью процедуры raymarching можно визуализировать объекты, имеющие такие функциональные представления (в виде SDF). В репозитории на GitHub (raymarch_sdf.ipynb) представлен пример того как работает raymarchng в двумерном случае на примере отрисовки окружности. Если бы мы находились в двумерном мире, располагались в начале координат и хотели бы отрисовать видимую часть окружности, то процесс с raymarching выглядел бы примерно так как на рисунке ниже:

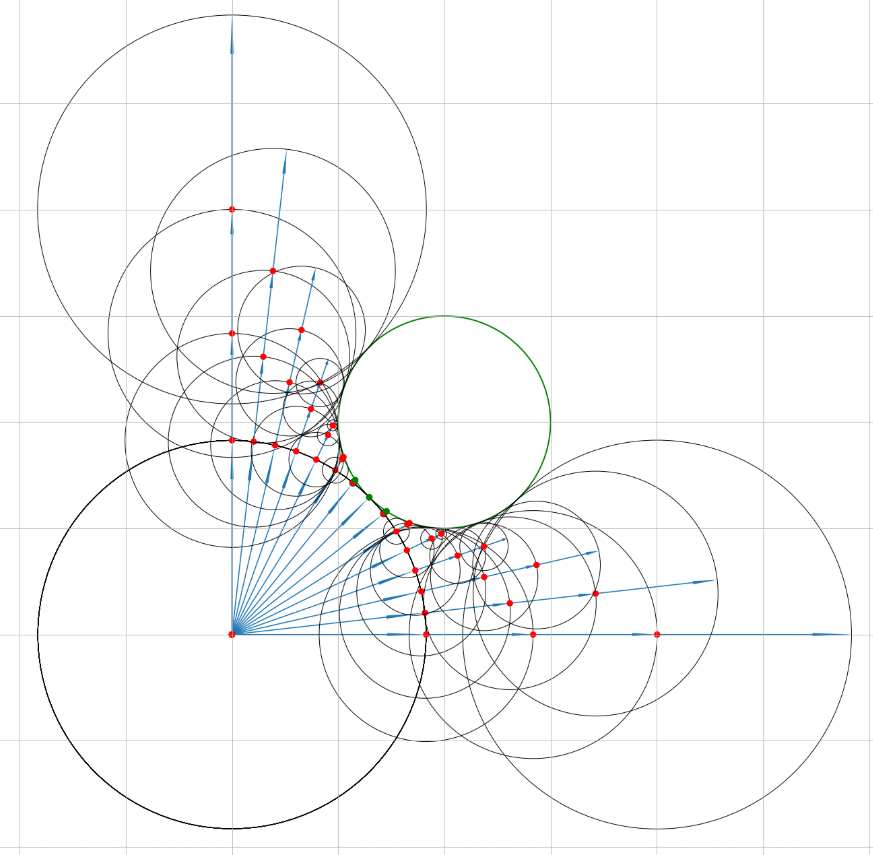
Красные точки обозначают местоположения, который проходит луч для того чтобы определить есть ли на его пути какой-то объект, описываемый с помощью SDF. Окружности вокруг каждой точки обозначают пространство в пределах которого точно нет никакого объекта. В каждой точке мы запрашиваем расстояние с помощью вычисления SDF до других объектов и берём минимальное значение (радиус окружности). Зелёные точки обозначают местоположения пересечения луча и видимо части окружности. Если таких лучей будет много, то мы можем восстановить видимый контур окружности. На практике достаточно было бы количества лучей равного разрешению экрана. В нашем плоском мире это полоска определённой длины. Например, 1024.

В 3D это имеет большее значение так как позволяет реализовать достаточно сложные эффекты. В этом видео можно найти пример построения неполигонального рендерера, основанного на визуализации с помощью известных SDF функциях объектов.

Ценность данного подхода к описанию трехмерных объектов особенно очевидна при работе с объектами, которые должны испытывать различные динамические деформации и слияния друг с другом (пример реализации на Unity) или при работе с объемными объектами (пример написания объемного рендеринга).

К преимуществам функционального подхода можно отнести:

• Компактное описание сложной пространственной структуры.
• Физически корректная модель.
• Масштабируемость модели.
• Возможность получить модель любого другого формата из данной.

К недостаткам функционального подхода можно отнести:

• Малое количество датасетов (обучающих выборок), использующих данный формат.
• Любые другие форматы крайне проблематично приводить к функциональному.
• Сложно работать с текстурами и шейдерами.

Преобразования форм 3D данных

Функциональное описание объектов можно назвать самым информативным, ведь из данной формы можно легко перейти к любой другой. Например, чтобы получить полигональную модель из функциональной, можно воспользоваться алгоритмом Multiresolution IsoSurface Extraction, предложенный авторами архитектуры Occupancy Net в [5], также существует множество альтернативных подходов, например [7].

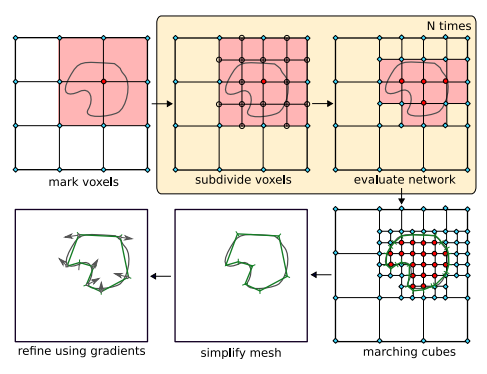
Рис.4 Схема работы алгоритма Multiresolution IsoSurface Extraction. Пространство с функциональной моделью разбивается на воксельную сеть. Воксельная сеть разбивается на более мелкие воксели по принципу октодеревьев. Итоговая сеть преобразуется в меш. Меш оптимизируется и используется для вычисления функции потерь.

Для перехода от полигональной модели к облаку точек, иногда можно отбросить все грани в описании пространственного графа двумя множествами: G — множество граней и V — множество вершин. Однако этот самый простой в реализации способ не является оптимальным, и в большинстве задач требуется применять иные методы. Например, как это было продемонстрировано в коде выше, можно сэмплировать дополнительные точки на гранях полигональной модели. Для перехода от полигональной модели к воксельному представлению существуют специальные алгоритмы вокселизации, которые сегодня нативно встроены в большинство программ для работы с 3D. Пример такого алгоритма можно посмотреть здесь.

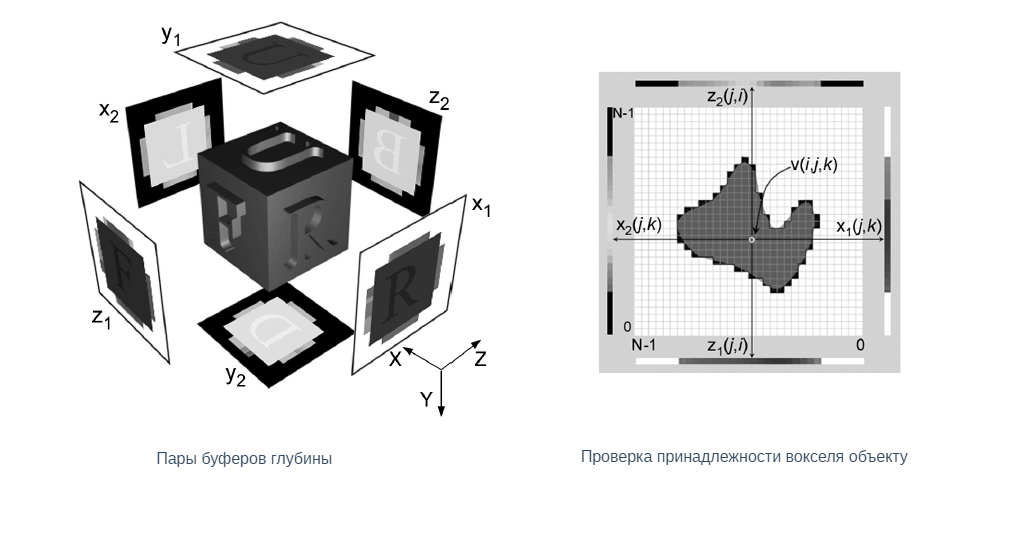
Рис.5 Пример алгоритма вокселизации. Для полигональной модели создаются 6 “буферов” — карт глубины объекта, которые используются для проверки принадлежности вокселя пространственной сети к итоговой модели.

Таким образом, выстраивается некоторая шкала информативности, изображённая на рис. 3. На этом же рисунке приведены примеры двумерных аналогов всех форм описания пространственных данных рассмотренных выше. Если же мы хотим пойти “снизу вверх”, то есть получить из менее информативной модели более информативную, мы вынуждены решать задачу аппроксимации данных. Помимо классических методов восстановления трехмерных данных, например метода радиальных базисных функций [8] или метода реконструкции из ориентированного облака точек [9], сегодня для решения этой задачи активно применяют подходы, основанные на данных (data driven), такие как нейронные сети. Так, архитектура Occupancy Net., о которой уже упоминалось выше, может не только восстанавливать функциональное представление по двумерным входным данным, но и решать эту же задачу для облака точек на входе.

Заключение

Понять, как устроены данные — одна из первых и главных задач для data science специалиста. Выше были рассмотрены основные формы представления трехмерных данных и их особенности, что в будущем лучше поможет нам понять алгоритмы машинного обучения, направленные на работу с подобными типами данных.

Следующим шагом после выбора формы представления данных с которыми работает исследователь является выбор функции расстояния на данных: функции, которая позволит ответить на вопрос — насколько две трехмерные модели похожи друг на друга? О том, какие есть функции расстояния и ошибок в пространстве трехмерных моделей, и как на их основе конструировать метрики качества, мы поговорим в следующей заметке.

Ниже приведен список источников, в котором помимо непосредственно упомянутых в тексте статей и книг, присутствует много других источников на тематику 3D ML, которые будут полезны всем интересующимся задачами 3D ML в общем, и 2D-to-3D в частности.