Всем хорошо известно, что индексы на основе структуры данных В-дерево помогают нам быстрее читать и находить записи в таблицах. В сети можно найти огромное количество информации по этому поводу, но я постараюсь показать, с какими проблемами нам пришлось бы столкнуться без использования индексов на основе В-дерева, и почему выбрали эту структуру данных. И в качестве примера я возьму подсистему хранения InnoDB из MySQL.
Чтобы разобраться, как появились индексы на основе В-дерева, давайте представим мир без них и попробуем решить типовую задачу. Попутно обсудим проблемы, с которыми столкнемся, и способы их решения.

В мире баз данных выделяют два самых распространенных способа хранения информации:
Преимущество первого способа в том, что он позволяет просто и быстро читать и сохранять данные. Новую информацию можно записывать только в конец файла (последовательная запись), что обеспечивает высокую скорость записи. Этот способ используют такие базы, как Leveldb, Rocksdb, Cassandra.
При втором способе (на основе страниц) данные разделяются на части фиксированного размера и сохраняются на диск. Эти части и называют «страницами» или «блоками». Они содержат записи (строки, кортежи) из таблиц.
Такой способ хранения данных используют MySQL, PostgreSQL, Oracle и другие. И поскольку мы говорим про индексы в MySQL, именно этот подход мы и рассмотрим.
Итак, все данные в MySQL сохраняются на диск в виде страниц. Размер страницы регулируется настройками базы данных и по умолчанию равен 16 Кб.
Каждая страница содержит в себе 38 байтов заголовков и 8-байтовое окончание (как показано на рисунке). А пространство, отведенное для хранения данных заполняется не полностью, потому что MySQL на каждой странице оставляет пустое место для будущих изменений.
Далее в расчетах мы будем пренебрегать служебной информацией, предполагая, что все 16 Кб страницы заполнены нашими данными. Мы не будем углубляться в организацию страниц InnoDB, это тема для отдельной статьи. Подробнее об этом вы можете почитать здесь.

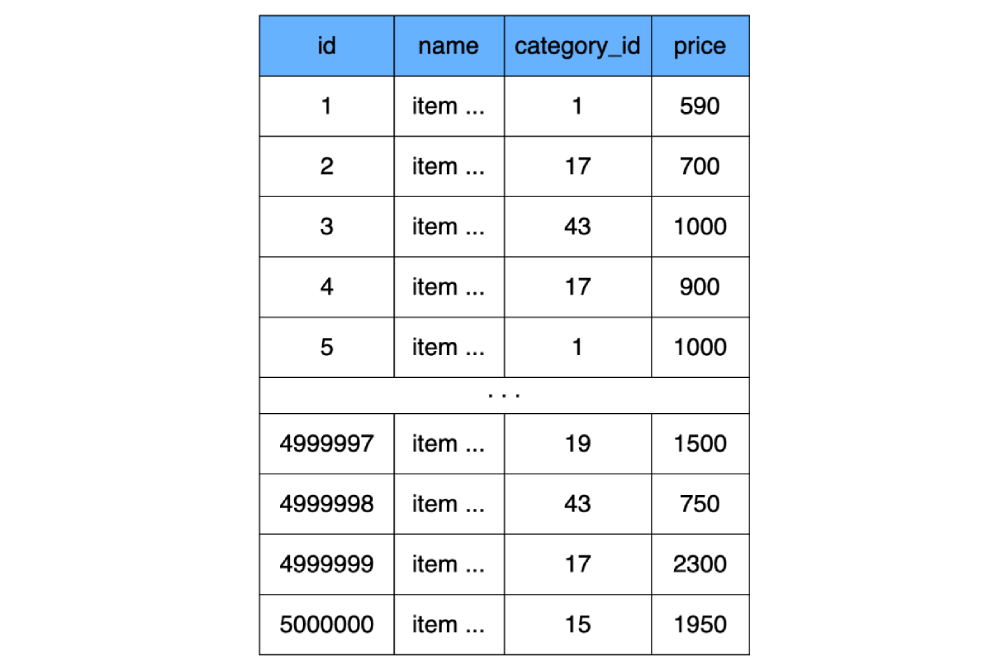
Поскольку мы выше договорились, что индексы еще не существуют, то для примера создадим простую табличку без всяких индексов (на самом деле, MySQL все равно создаст индекс, но мы его не будем учитывать в расчетах):
и выполним такой запрос:
MySQL откроет файл, где хранятся данные из таблицы
С какими же проблемами мы при этом можем столкнуться?
Так как у нас все хранится на жестком диске, давайте посмотрим на его устройство. Жесткий диск читает и пишет данные по секторам (блокам). Размер такого сектора может быть от 512 байтов до 8 Кб (в зависимости от диска). Несколько идущих подряд секторов могут объединяться в кластеры.
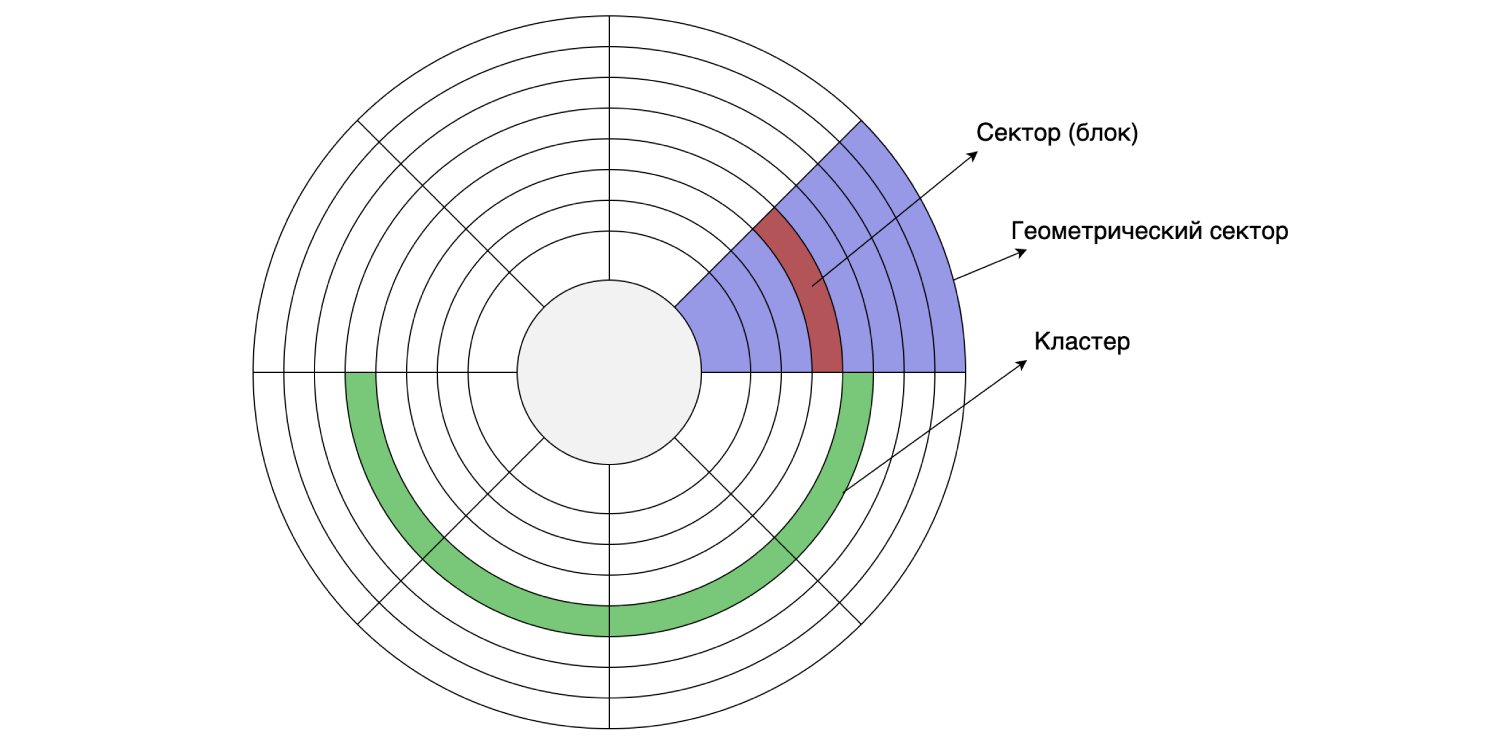
Размер кластера можно задать при форматировании/разметке диска, то есть это делается программно. Предположим, что размер сектора на диске равен 4 Кб, а файловая система размечена с размером кластера 16 Кб: один кластер состоит из четырех секторов. Как мы помним, MySQL по умолчанию хранит данные на диске страницами по 16 Кб, поэтому одна страница помещается в один кластер диска.
Давайте посчитаем, сколько пространства займет наша табличка с продуктами при условии, что в ней хранится 500 000 позиций. Мы имеем три четырехбайтных поля
Таким образом, для хранения этой таблички необходимо 9750 кластеров на жестком диске (9750 страниц по 16 Кб).
При сохранении на диск берутся свободные кластеры, что приводит к «размазыванию» кластеров одной таблички (файла) по всему диску (это называют фрагментацией). Чтение таких случайно расположенных на диске блоков памяти называют случайным чтением (random read). Такое чтение получается медленнее, потому что требуется многократно перемещать головку жесткого диска. Чтобы считать весь файл, нам приходится прыгать по всему диску для получения нужных кластеров.
Вернемся к нашему SQL-запросу. Для нахождения всех строк серверу придется считать все 9750 кластеров, разбросанных по всему диску, при этом будет затрачено много времени на перемещение считывающей головки диска. Чем больше кластеров используют наши данные, тем медленнее будет осуществляться поиск по ним. И кроме того, наша операция забьет систему ввода/вывода операционной системы.
В конечном итоге мы получаем низкую скорость чтения данных; «подвешиваем» ОС, забивая систему ввода/вывода; и производим много сравнений, проверяя условия запроса для каждой строки.
Как мы можем самостоятельно решить эту проблему?
Нужно придумать, как улучшить поиск по таблице
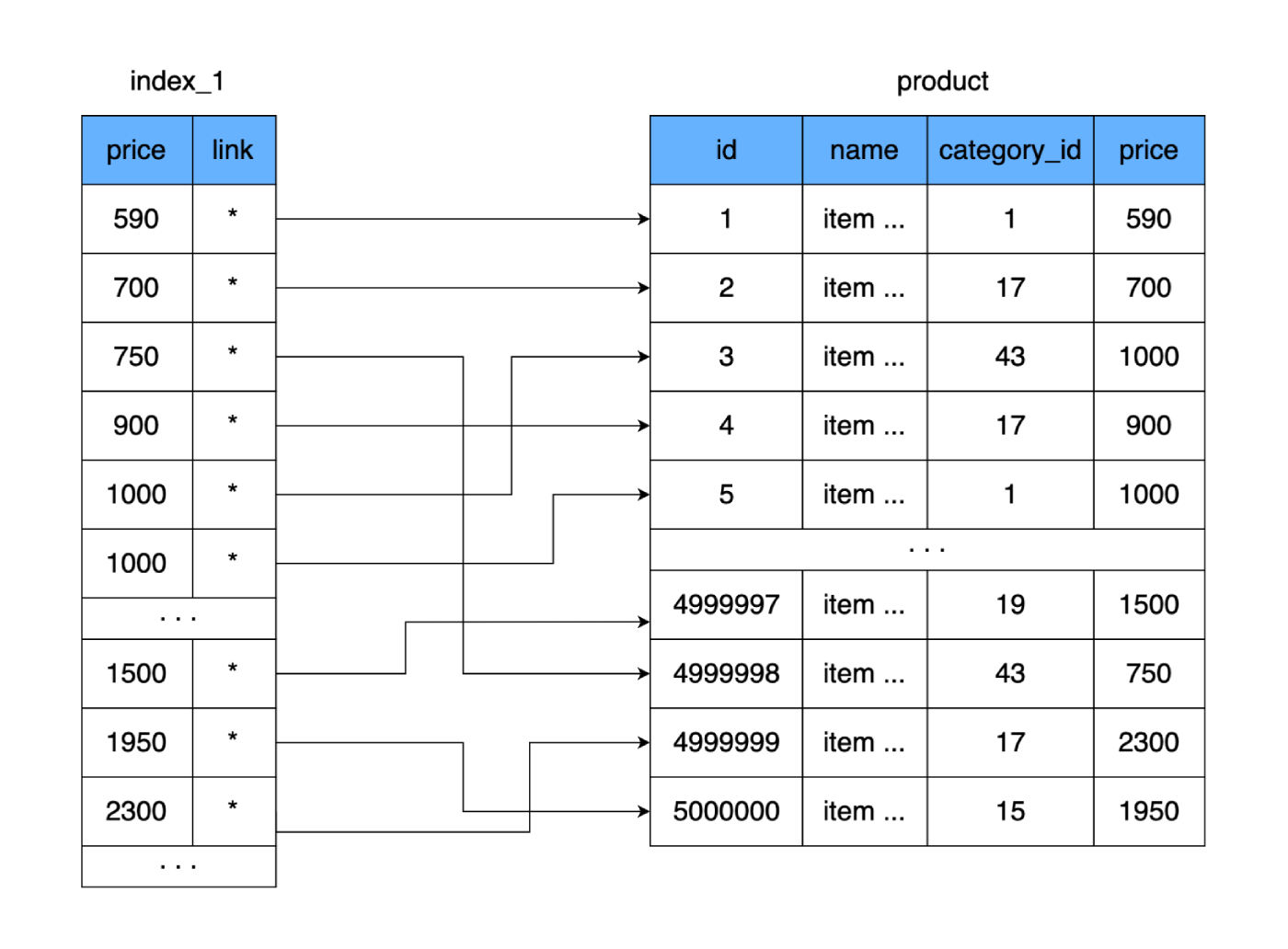
Что нам это дает? Новая таблица, как и основная, хранится на диске постранично (блоками). В ней записаны цена и ссылка на основную таблицу. Давайте посчитаем, сколько места займет такая таблица. Цена занимает 4 байта, и пусть ссылка на основную таблицу (адрес) тоже будет размером 4 байта. Для 500 000 строк наша новая таблица будет весить всего 4 Мб. Тогда на одну страницу с данными поместится намного больше строк из новой таблицы, и потребуется меньше страниц для хранения всех наших цен.
Если для полной таблицы требуется 9750 кластеров на жестком диске (а в худшем случае это 9750 прыжков по жесткому диску), то новая таблица помещается всего на 250 кластеров. За счет этого многократно уменьшится количество использованных кластеров на диске, а значит и время, затраченное на случайное чтение. Даже если мы будем читать всю нашу новую табличку и сравнивать значения для поиска нужной цены, то в худшем случае понадобится 250 прыжков по кластерам новой таблицы. И после нахождения нужного адреса прочитаем еще один кластер, где лежат полные данные. Результат: 251 считывание против изначальных 9750. Разница существенная.
Помимо этого, для поиска по такой таблице можно воспользоваться, например, алгоритмом бинарного поиска (так как список отсортированный). Так мы еще больше сэкономим на количестве чтений и операциях сравнения.
Давайте назовем нашу вторую таблицу индексом.
Ура! Мы придумали свой собственныйвелосипед индекс!
Но стоп: ведь по мере роста таблицы индекс тоже будет все больше и больше, и в конечном итоге мы снова вернемся к исходной проблеме. Поиск опять будет занимать много времени.
А если создать еще один индекс над уже имеющимся?
Только на этот раз запишем не каждое значение поля
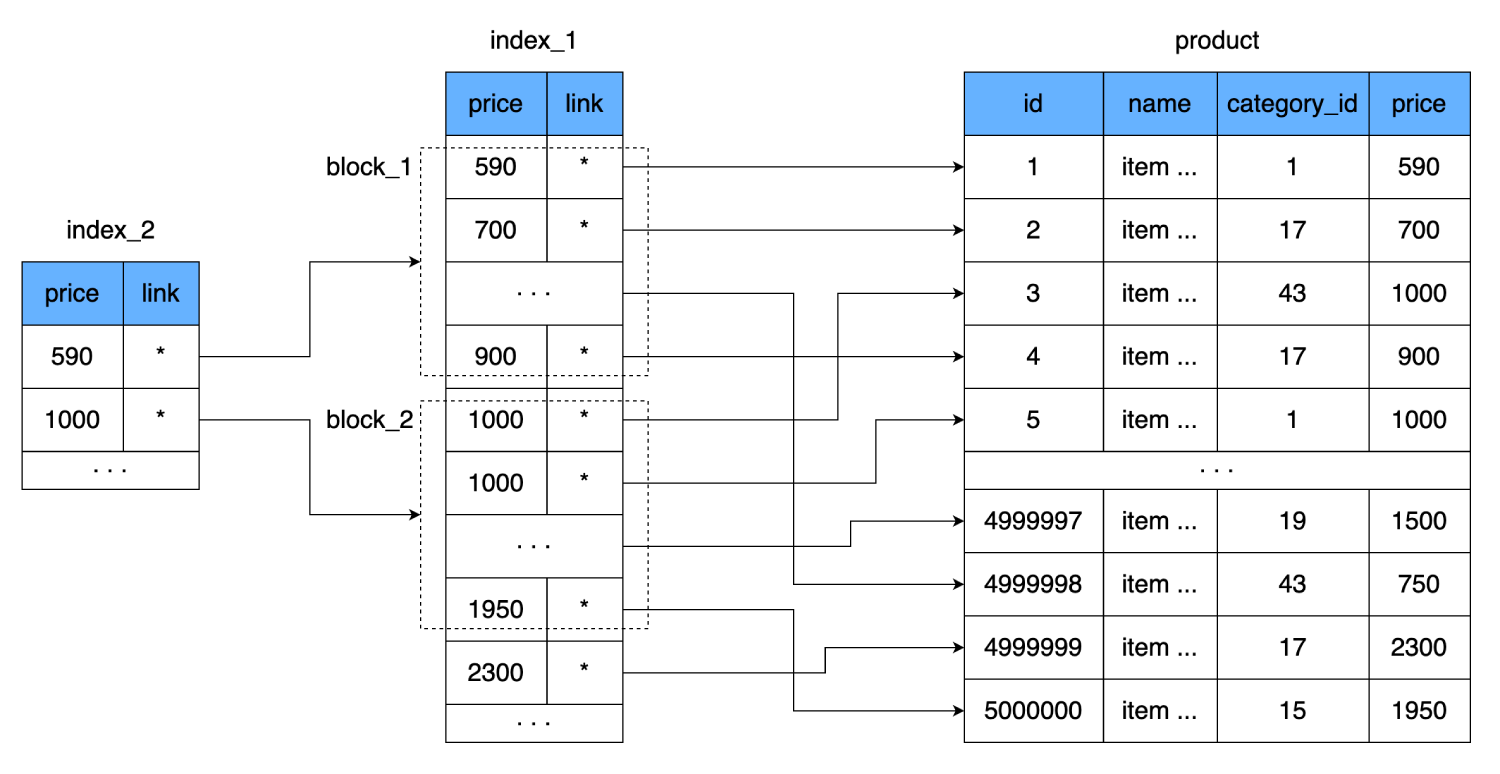
Это еще уменьшит количество чтений. Одна строка нашего индекса занимает 8 байтов, то есть на одну 16-килобайтовую страницу мы можем вместить 2000 таких строк. Новый индекс будет содержать в себе ссылку на блок из 2000 строк первого индекса и цену, с которой этот блок начинается. Одна такая строка тоже занимает 8 байтов, но их количество резко уменьшается: вместо 500 000 всего 250. Они даже помещаются в один кластер жесткого диска. Таким образом, чтобы найти нужную цену мы сможем точно определить, в каком блоке из 2000 строк она находится. И в худшем случае, для нахождения все той же записи мы:
Получим всего 3 прыжка по кластерам.
Но и этот уровень рано или поздно тоже наполнится множеством данных. Поэтому нам придется повторить все сделанное, добавляя новый уровень снова и снова. То есть нам нужна такая структура данных для хранения индекса, которая будет добавлять новые уровни по мере увеличения размера индекса и самостоятельно при этом балансировать данные между ними.
Если мы перевернем таблички, чтобы сверху был последний индекс, а снизу основная таблица с данными, то получится структура, очень похожая на дерево.
По похожему принципу работает структура данных B-дерево, поэтому ее выбрали для этих целей.
Чаще всего в MySQL используются индексы, упорядоченные на основе B-дерева (сбалансированное дерево поиска).
Общая идея В-дерева похожа на наши таблички индексов. Значения хранятся по порядку и все листья дерева находятся на одинаковом расстоянии от корня.
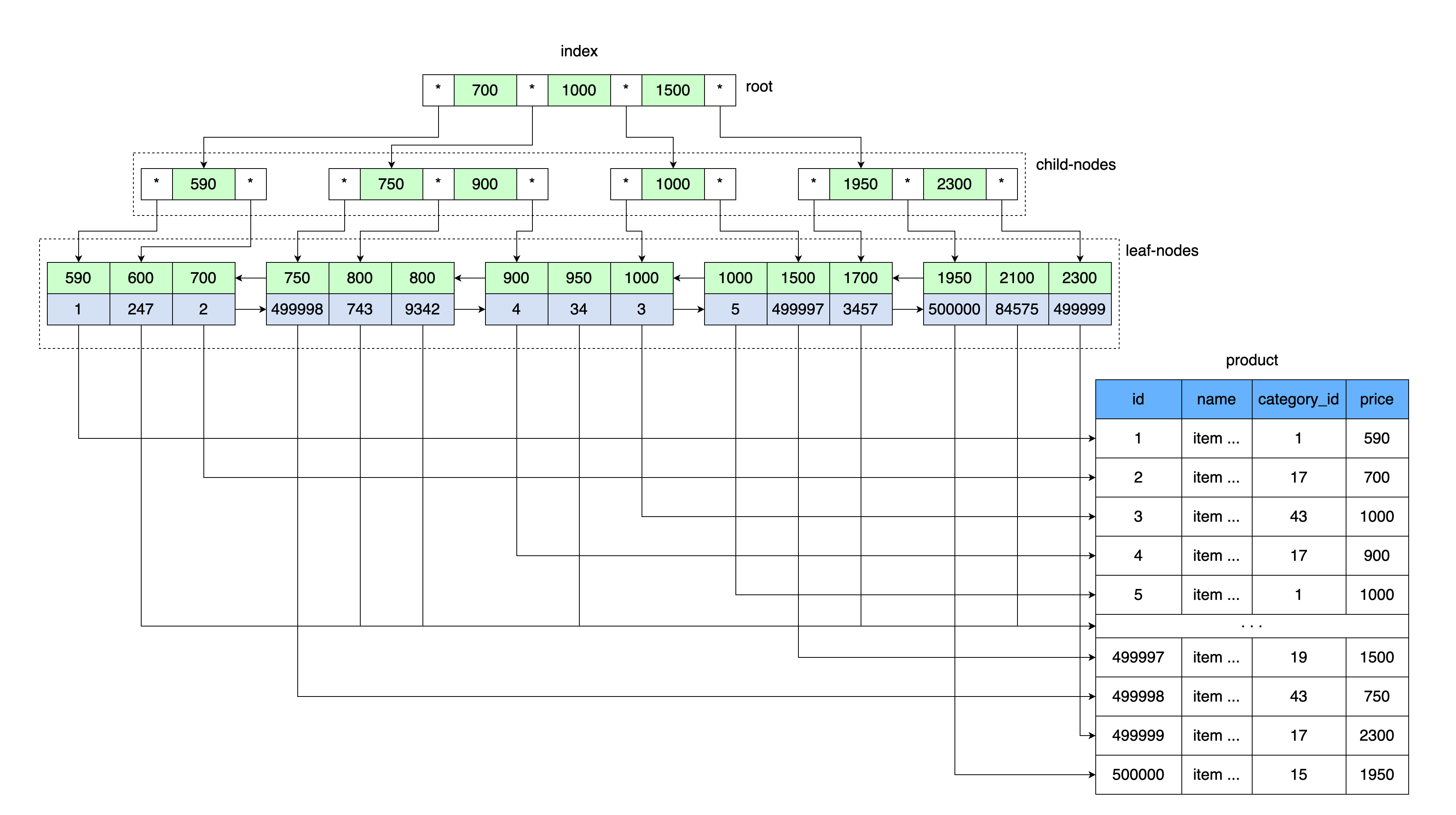
Подобно тому, как наша таблица с индексом хранила значение цены и ссылку на блок данных, в которой находится диапазон значений с этой ценой, так и в корне В-дерева хранится значение цены и ссылка на область памяти на диске.
Сначала читается страница, в которой находится корень В-дерева. Далее по вхождению в диапазон ключей находится указатель на нужный дочерний узел. Читается страница дочернего узла, откуда по значению ключа берется ссылка на лист с данными, и по этой ссылке читается страница с данными.
Если быть точнее, то в InnoDB используется структура данных B+дерево (B+tree).
Каждый раз, создавая таблицу вы автоматически создаете В+дерево, потому что MySQL хранит такой индекс для первичного и вторичного ключей.
Вторичные ключи дополнительно хранят в себе еще и значения первичного (кластерного) ключа в качестве ссылки на строку с данными. Следовательно, вторичный ключ увеличивается на размер значения первичного ключа.
Кроме того, в В+деревьях используются дополнительные ссылки между дочерними узлами, что увеличивает скорость поиска по диапазону значений. Подробнее о структуре b+tree индексов в InnoDB читайте здесь.
Индекс на основе b-дерева дает большое преимущество при поиске данных по диапазону значений за счет многократного снижения количества считываемой информации с диска. Он участвует не только во время поиска по условию, но и при сортировках, соединениях, группировках. Как MySQL использует индексы читайте здесь.
Большая часть запросов к базе — это как раз запросы на поиск информации по значению или по диапазону значений. Поэтому в MySQL самым часто используемым индексом является индекс на основе b-дерева.
Также, b-tree индекс помогает при получении данных. Так как в листьях индекса хранятся первичный ключ (кластерный индекс) и само значение колонки, по которой построен некластерный индекс (вторичный ключ), то за этими данными можно уже не обращаться к основной таблице и брать их из индекса. Это называется покрывающим индексом. Подробнее о кластерных и некластерных индексах можно найти в этой статье.
Индексы, как и таблицы, тоже хранятся на диске и занимают место. При каждом добавлении информации в таблицу индекс нужно поддерживать в актуальном состоянии, следить за правильностью всех ссылок между узлами. Это создает накладные расходы при записи информации, что является основным недостатком индексов на основе b-дерева. Мы жертвуем скоростью записи для увеличения скорости чтения.
Чтобы разобраться, как появились индексы на основе В-дерева, давайте представим мир без них и попробуем решить типовую задачу. Попутно обсудим проблемы, с которыми столкнемся, и способы их решения.

Введение
В мире баз данных выделяют два самых распространенных способа хранения информации:
- На основе Log based-структур.
- На основе страниц.
Преимущество первого способа в том, что он позволяет просто и быстро читать и сохранять данные. Новую информацию можно записывать только в конец файла (последовательная запись), что обеспечивает высокую скорость записи. Этот способ используют такие базы, как Leveldb, Rocksdb, Cassandra.
При втором способе (на основе страниц) данные разделяются на части фиксированного размера и сохраняются на диск. Эти части и называют «страницами» или «блоками». Они содержат записи (строки, кортежи) из таблиц.
Такой способ хранения данных используют MySQL, PostgreSQL, Oracle и другие. И поскольку мы говорим про индексы в MySQL, именно этот подход мы и рассмотрим.
Хранение данных в MySQL
Итак, все данные в MySQL сохраняются на диск в виде страниц. Размер страницы регулируется настройками базы данных и по умолчанию равен 16 Кб.
Каждая страница содержит в себе 38 байтов заголовков и 8-байтовое окончание (как показано на рисунке). А пространство, отведенное для хранения данных заполняется не полностью, потому что MySQL на каждой странице оставляет пустое место для будущих изменений.
Далее в расчетах мы будем пренебрегать служебной информацией, предполагая, что все 16 Кб страницы заполнены нашими данными. Мы не будем углубляться в организацию страниц InnoDB, это тема для отдельной статьи. Подробнее об этом вы можете почитать здесь.

Поскольку мы выше договорились, что индексы еще не существуют, то для примера создадим простую табличку без всяких индексов (на самом деле, MySQL все равно создаст индекс, но мы его не будем учитывать в расчетах):
CREATE TABLE `product` (
`id` INT NOT NULL AUTO_INCREMENT,
`name` CHAR(100) CHARACTER SET utf8 COLLATE utf8_general_ci NOT NULL,
`category_id` INT NOT NULL,
`price` INT NOT NULL,
) ENGINE=InnoDB;
и выполним такой запрос:
SELECT * FROM product WHERE price = 1950;MySQL откроет файл, где хранятся данные из таблицы
product, и начнет перебирать все записи (строки) в поисках нужных, сравнивая поле price из каждой найденной строки со значением в запросе. Для наглядности я специально рассматриваю вариант с полным сканированием файла, так что случаи, когда MySQL получает данные из кэша, нам не подходят.С какими же проблемами мы при этом можем столкнуться?
Жесткий диск
Так как у нас все хранится на жестком диске, давайте посмотрим на его устройство. Жесткий диск читает и пишет данные по секторам (блокам). Размер такого сектора может быть от 512 байтов до 8 Кб (в зависимости от диска). Несколько идущих подряд секторов могут объединяться в кластеры.

Размер кластера можно задать при форматировании/разметке диска, то есть это делается программно. Предположим, что размер сектора на диске равен 4 Кб, а файловая система размечена с размером кластера 16 Кб: один кластер состоит из четырех секторов. Как мы помним, MySQL по умолчанию хранит данные на диске страницами по 16 Кб, поэтому одна страница помещается в один кластер диска.
Давайте посчитаем, сколько пространства займет наша табличка с продуктами при условии, что в ней хранится 500 000 позиций. Мы имеем три четырехбайтных поля
id, price и category_id. Условимся, что поле name у всех записей заполнено до конца (все 100 символов), и каждый символ занимает 3 байта. (3*4) + (100*3) = 312 байт — столько весит одна строка нашей таблицы, и умножив это на 500 000 строк получим вес таблицы product 156 мегабайтов.Таким образом, для хранения этой таблички необходимо 9750 кластеров на жестком диске (9750 страниц по 16 Кб).
При сохранении на диск берутся свободные кластеры, что приводит к «размазыванию» кластеров одной таблички (файла) по всему диску (это называют фрагментацией). Чтение таких случайно расположенных на диске блоков памяти называют случайным чтением (random read). Такое чтение получается медленнее, потому что требуется многократно перемещать головку жесткого диска. Чтобы считать весь файл, нам приходится прыгать по всему диску для получения нужных кластеров.

Вернемся к нашему SQL-запросу. Для нахождения всех строк серверу придется считать все 9750 кластеров, разбросанных по всему диску, при этом будет затрачено много времени на перемещение считывающей головки диска. Чем больше кластеров используют наши данные, тем медленнее будет осуществляться поиск по ним. И кроме того, наша операция забьет систему ввода/вывода операционной системы.
В конечном итоге мы получаем низкую скорость чтения данных; «подвешиваем» ОС, забивая систему ввода/вывода; и производим много сравнений, проверяя условия запроса для каждой строки.
Сам себе велосипед
Как мы можем самостоятельно решить эту проблему?
Нужно придумать, как улучшить поиск по таблице
product. Создадим еще одну таблицу, в которой будем хранить только поле price и ссылку на запись (область на диске) в нашей таблице product. Примем сразу за правило, что при добавлении данных в новую таблицу мы будем хранить цены в отсортированном виде.
Что нам это дает? Новая таблица, как и основная, хранится на диске постранично (блоками). В ней записаны цена и ссылка на основную таблицу. Давайте посчитаем, сколько места займет такая таблица. Цена занимает 4 байта, и пусть ссылка на основную таблицу (адрес) тоже будет размером 4 байта. Для 500 000 строк наша новая таблица будет весить всего 4 Мб. Тогда на одну страницу с данными поместится намного больше строк из новой таблицы, и потребуется меньше страниц для хранения всех наших цен.
Если для полной таблицы требуется 9750 кластеров на жестком диске (а в худшем случае это 9750 прыжков по жесткому диску), то новая таблица помещается всего на 250 кластеров. За счет этого многократно уменьшится количество использованных кластеров на диске, а значит и время, затраченное на случайное чтение. Даже если мы будем читать всю нашу новую табличку и сравнивать значения для поиска нужной цены, то в худшем случае понадобится 250 прыжков по кластерам новой таблицы. И после нахождения нужного адреса прочитаем еще один кластер, где лежат полные данные. Результат: 251 считывание против изначальных 9750. Разница существенная.
Помимо этого, для поиска по такой таблице можно воспользоваться, например, алгоритмом бинарного поиска (так как список отсортированный). Так мы еще больше сэкономим на количестве чтений и операциях сравнения.
Давайте назовем нашу вторую таблицу индексом.
Ура! Мы придумали свой собственный
Но стоп: ведь по мере роста таблицы индекс тоже будет все больше и больше, и в конечном итоге мы снова вернемся к исходной проблеме. Поиск опять будет занимать много времени.
Еще один индекс
А если создать еще один индекс над уже имеющимся?
Только на этот раз запишем не каждое значение поля
price, а одно значение свяжем с целой страницей (блоком) из индекса. То есть появится дополнительный уровень индекса, который будет указывать на набор данных из предыдущего индекса (страницу на диске, где хранятся данные из первого индекса). 
Это еще уменьшит количество чтений. Одна строка нашего индекса занимает 8 байтов, то есть на одну 16-килобайтовую страницу мы можем вместить 2000 таких строк. Новый индекс будет содержать в себе ссылку на блок из 2000 строк первого индекса и цену, с которой этот блок начинается. Одна такая строка тоже занимает 8 байтов, но их количество резко уменьшается: вместо 500 000 всего 250. Они даже помещаются в один кластер жесткого диска. Таким образом, чтобы найти нужную цену мы сможем точно определить, в каком блоке из 2000 строк она находится. И в худшем случае, для нахождения все той же записи мы:
- Выполним одно чтение из нового индекса.
- Пробежав по 250 строкам найдем ссылку на блок данных из второго индекса.
- Считаем один кластер, в котором хранится 2000 строк с ценами и ссылками на основную таблицу.
- Проверив эти 2000 строк, найдем нужную и еще один раз прыгнем по диску, чтобы прочитать последний блок с данными.
Получим всего 3 прыжка по кластерам.
Но и этот уровень рано или поздно тоже наполнится множеством данных. Поэтому нам придется повторить все сделанное, добавляя новый уровень снова и снова. То есть нам нужна такая структура данных для хранения индекса, которая будет добавлять новые уровни по мере увеличения размера индекса и самостоятельно при этом балансировать данные между ними.
Если мы перевернем таблички, чтобы сверху был последний индекс, а снизу основная таблица с данными, то получится структура, очень похожая на дерево.
По похожему принципу работает структура данных B-дерево, поэтому ее выбрали для этих целей.
Коротко о В-деревьях
Чаще всего в MySQL используются индексы, упорядоченные на основе B-дерева (сбалансированное дерево поиска).
Общая идея В-дерева похожа на наши таблички индексов. Значения хранятся по порядку и все листья дерева находятся на одинаковом расстоянии от корня.

Подобно тому, как наша таблица с индексом хранила значение цены и ссылку на блок данных, в которой находится диапазон значений с этой ценой, так и в корне В-дерева хранится значение цены и ссылка на область памяти на диске.
Сначала читается страница, в которой находится корень В-дерева. Далее по вхождению в диапазон ключей находится указатель на нужный дочерний узел. Читается страница дочернего узла, откуда по значению ключа берется ссылка на лист с данными, и по этой ссылке читается страница с данными.
В-дерево в InnoDB
Если быть точнее, то в InnoDB используется структура данных B+дерево (B+tree).
Каждый раз, создавая таблицу вы автоматически создаете В+дерево, потому что MySQL хранит такой индекс для первичного и вторичного ключей.
Вторичные ключи дополнительно хранят в себе еще и значения первичного (кластерного) ключа в качестве ссылки на строку с данными. Следовательно, вторичный ключ увеличивается на размер значения первичного ключа.
Кроме того, в В+деревьях используются дополнительные ссылки между дочерними узлами, что увеличивает скорость поиска по диапазону значений. Подробнее о структуре b+tree индексов в InnoDB читайте здесь.
Подводим итоги
Индекс на основе b-дерева дает большое преимущество при поиске данных по диапазону значений за счет многократного снижения количества считываемой информации с диска. Он участвует не только во время поиска по условию, но и при сортировках, соединениях, группировках. Как MySQL использует индексы читайте здесь.
Большая часть запросов к базе — это как раз запросы на поиск информации по значению или по диапазону значений. Поэтому в MySQL самым часто используемым индексом является индекс на основе b-дерева.
Также, b-tree индекс помогает при получении данных. Так как в листьях индекса хранятся первичный ключ (кластерный индекс) и само значение колонки, по которой построен некластерный индекс (вторичный ключ), то за этими данными можно уже не обращаться к основной таблице и брать их из индекса. Это называется покрывающим индексом. Подробнее о кластерных и некластерных индексах можно найти в этой статье.
Индексы, как и таблицы, тоже хранятся на диске и занимают место. При каждом добавлении информации в таблицу индекс нужно поддерживать в актуальном состоянии, следить за правильностью всех ссылок между узлами. Это создает накладные расходы при записи информации, что является основным недостатком индексов на основе b-дерева. Мы жертвуем скоростью записи для увеличения скорости чтения.
Список используемой литературы
- MySQL по максимуму. 3-е издание
Автор: Зайцев Пётр, Ткаченко Вадим и Шварц Бэрон
Год выпуска: 2018 - blog.jcole.us/innodb
- dev.mysql.com/doc/refman/8.0/en/innodb-storage-engine.html


bullgare
Вообще-то, если нет covering index, то для чтения всех записей с ценой больше 1950 понадобится не 251 чтение с диска, а, в худшем случае, 10000: 250+9750. Поэтому MySQL производит предварительную оценку статистики, сколько процентов записей данный запрос может вернуть. И иногда делает full table scan вместо использования индекса.
hanagantig Автор
Да, MySQL использует статистику. Но цель рассматриваемого примера в статье — наглядно показать уменьшение количества чтений. И для этого «изобретался» способ решить возникшую проблему. А именно, вынести цены в отдельную табличку index_1, которая помещается на 250 кластерах диска, прочитать ее полностью, найти цену 1950 и по соответствующей ссылке получить данные из основной таблицы. Поэтому в расчетах получили чтение 251 кластера.
bullgare
Данные лежат на диске. Для их чтения (select *) нужно чтение с диска. В худшем случае — 9750 штук.
hanagantig Автор
Выбор происходит по условию price = 1950. Находим цену в индексе и, если нет covering index, то за данными (select *) будет одно обращение к диску (если в табличке одна запись с ценой 1950).
bullgare
Поэтому я и говорю, про худший случай (у всех товаров цена 1950) и про оценку статистики.
hanagantig Автор
В таблице обозначена одна запись с ценой 1950 (смотрите рисунки).
bullgare
Поэтому я и говорю, про худший случай (у всех товаров цена 1950) и про оценку статистики.