Привет, Хаброжители! Квантовые компьютеры спровоцировали новую компьютерную революцию, и у вас есть прекрасный шанс присоединиться к технологическому прорыву прямо сейчас. Разработчики, специалисты по компьютерной графике и начинающие айтишники найдут в этой книге практическую информацию по квантовым вычислениям, нужную программистам. Вместо штудирования теории и формул вы сразу займетесь конкретными задачами, демонстрирующими уникальные возможности квантовой технологии.

Эрик Джонстон, Ник Хэрриган и Мерседес Химено-Сеговиа помогают развить необходимые навыки и интуицию, а также освоить инструментарий, необходимый для создания квантовых приложений. Вы поймете, на что способны квантовые компьютеры и как это применить в реальной жизни. Книга состоит из трех частей: — Программирование QPU: основные концепции программирования квантовых процессоров, выполнение операций с кубитами и квантовая телепортация. — Примитивы QPU: алгоритмические примитивы и методы, усиление амплитуды, квантовое преобразование Фурье и оценка фазы. — Практика QPU: решение конкретных задач с помощью примитивов QPU, методы квантового поиска и алгоритм разложения Шора.

Реальные данные

Полноценные приложения для QPU строятся для работы с реальными, не учебными данными. Реальные данные далеко не всегда ограничиваются базовыми целыми числами, которыми мы обходились до сих пор. Следовательно, вопрос о том, как представить более сложные данные в QPU, стоит потраченных усилий, и хорошие структуры данных могут быть не менее важны, чем хорошие алгоритмы. В этой главе мы постараемся ответить на два вопроса, которые ранее обходили стороной:

1. Как представить сложные типы данных в регистре QPU? Положительное целое число можно представить в простой двоичной кодировке. Но что делать с иррациональными числами или даже с составными типами данных вроде векторов или матриц? Этот вопрос обретает новую глубину, если учесть, что суперпозиция и относительная фаза могут предоставить новые квантовые варианты кодирования таких типов данных.
2. Как прочитать данные, хранящиеся в регистре QPU? До сих пор мы инициализировали свои входные регистры вручную, используя операции WRITE для ручной инициализации кубитов регистра нужными двоичными числами. Если вы собираетесь применять квантовые приложения с большими массивами данных, эти данные нужно будет прочитать в регистры QPU из памяти. Это нетривиальное требование, так как, возможно, регистр QPU нужно будет инициализировать суперпозицией значений, а для этого традиционная оперативная память не приспособлена.

Начнем с первого вопроса. При описании представлений QPU для типов данных возрастающей сложности мы придем к введению полноценных квантовых структур данных и концепции квантовой оперативной памяти (QRAM). Квантовая оперативная память является критическим ресурсом для многих практических применений QPU.

Материал последующих глав будет сильно зависеть от структур данных, представленных в этой главе. Например, так называемое комплексное амплитудное кодирование, которое будет описано для векторных данных, занимает центральное место во всех квантовых приложениях машинного обучения, представленных в главе 13.

Нецелые данные

Как закодировать нецелые числовые данные в регистре QPU? Два стандартных способа представления таких значений в двоичной форме — представления с фиксированной точкой и с плавающей точкой. Хотя представление с плавающей точкой обладает большей гибкостью (и способностью адаптироваться к диапазону значений, которые требуется представить с определенным количеством битов), из-за высокой ценности кубитов и нашего стремления к простоте представление с фиксированной точкой лучше подойдет для начала работы.

Числа с фиксированной точкой часто описываются в Q-записи (к сожалению, Q в данном случае не означает «квантовый»). Это помогает избавиться от неоднозначности относительно того, в какой позиции регистра кончаются биты дробной части и начинаются биты целой части. Запись Qn.m обозначает n-разрядный регистр, m разрядов которого предназначены для дробной части (а следовательно, оставшиеся (n – m) содержат целую часть). Конечно, при помощи той же записи можно указать, как регистр QPU должен использоваться для кодирования числа с фиксированной точкой. Например, на рис. 9.1 изображен восьмикубитный регистр QPU, в котором закодировано значение 3.640625 в представлении с фиксированной точкой Q8.6.

В приведенном примере выбранное число может быть точно закодировано в представлении с фиксированной точкой, потому что 3.640625 = Конечно, такое везение встречается не всегда. Увеличение количества битов в целой части регистра с фиксированной точкой расширяет диапазон целочисленных значений, которые могут быть им представлены, а увеличение количества битов в дробной части повышает точность представления дробной части числа. Чем больше кубитов в дробной части, тем больше вероятность того, что некоторая комбинация 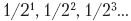сможет точно представить заданное число.


И хотя в следующих главах мы будем кратко упоминать об использовании представления с фиксированной точкой, оно играет чрезвычайно важную роль в экспериментах с реальными данными в небольших регистрах QPU. Работая с разными способами кодировки, необходимо внимательно следить за тем, какая конкретная кодировка использовалась для данных в конкретном регистре QPU, чтобы правильно интерпретировать состояние его кубитов.

QRAM

В регистрах QPU можно хранить представления разных числовых значений, но как записать в них эти значения? Данные, инициализированные вручную, очень быстро устаревают. В действительности нам нужна возможность читать значения из памяти, с выборкой хранимых значений по двоичному адресу. Программист работает с традиционной оперативной памятью при помощи двух регистров: один инициализируется адресом памяти, а другой остается неинициализированным. Оперативная память записывает во второй регистр двоичные данные, хранящиеся по адресу, заданному первым регистром, как показано на рис. 9.2.


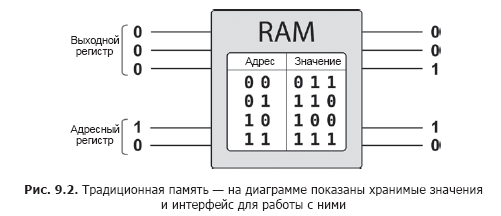
Можно ли использовать традиционную память для хранения значений, предназначенных для инициализации регистров QPU? Конечно, идея выглядит привлекательно.

Если вы хотите инициализировать регистр QPU только одним традиционным значением (в дополнительном коде, в представлении с фиксированной точкой или в простой двоичной кодировке), то оперативная память прекрасно подойдет. Нужное значение просто хранится в памяти, а для его записи или чтения из регистра QPU используются операции write() и read(). Именно этот ограниченный механизм использовался кодом QCEngine JavaScript для взаимодействия с регистрами QPU до настоящего момента.

Так, пример кода из листинга 9.1, который получает массив a и реализует операцию a[2] += 1;, неявно извлекает этот массив значений из оперативной памяти для инициализации регистра QPU. Схема изображена на рис. 9.3.

Пример кода

Этот пример можно выполнить онлайн по адресу http://oreilly-qc.github.io?p=9-1.
Листинг 9.1. Использование QPU для увеличения числа в памяти

var a = [4, 3, 5, 1];

qc.reset(3);
var qreg = qint.new(3, 'qreg');

qc.print(a);
increment(2, qreg);
qc.print(a);

function increment(index, qreg)
{
      qreg.write(a[index]);
      qreg.add(1);
      a[index] = qreg.read();
}

Стоит заметить, что в этом простом случае не только традиционная оперативная память используется для хранения целого числа, но и традиционный процессор выполняет индексирование массива для выбора и передачи QPU нужного значения.

Хотя такое использование оперативной памяти позволяет инициализировать регистры QPU простыми двоичными значениями, у него есть серьезные ограничения. Что, если потребуется инициализировать регистр QPU суперпозицией хранимых значений? Например, предположим, что в оперативной памяти значение 3 (110) хранится по адресу 0x01, а значение 5 (111) — по адресу 0x11. Как подготовить входной регистр в суперпозиции этих двух значений?

С традиционной оперативной памятью и неуклюжей традиционной операцией write() это сделать не удастся. Квантовым процессорам, как и когда-то их ламповым предкам, понадобится принципиально новое оборудование памяти — квантовое по своей природе. Знакомьтесь: квантовая оперативная память (QRAM) позволяет читать и записывать данные на квантовом уровне. Уже есть несколько идей относительно того, как физически строить QRAM, но стоит заметить, что история вполне может повториться, и невероятно мощные квантовые процессоры могут появиться задолго до того, как появится работоспособное оборудование квантовой памяти.

Стоит чуть точнее объяснить, что же делает QRAM. Как и традиционная память, QRAM получает на входе два регистра: адресный регистр QPU для адреса памяти и выходной регистр QPU, в котором возвращается значение, хранящееся по заданному адресу. Для QRAM оба регистра состоят из кубитов. Это означает, что в адресном регистре можно задать суперпозицию ячеек памяти и как следствие получить в выходном регистре суперпозицию соответствующих значений (рис. 9.4).


Таким образом, QRAM фактически позволяет читать хранимые значения в суперпозиции. Точные комплексные амплитуды суперпозиции, которая будет получена в выходном регистре, определяются суперпозицией, предоставленной в адресном регистре. На рис. 9.2 показаны различия при выполнении той же операции инкремента в листинге 9.1 (рис. 9.5), но для обращения к данным используется QRAM вместо операций чтения/записи QPU. Буквой «A» обозначен регистр, в котором QRAM передается адрес (или суперпозиция). Буквой «D» обозначен регистр, в котором QRAM возвращает соответствующую суперпозицию хранимых значений (данных).

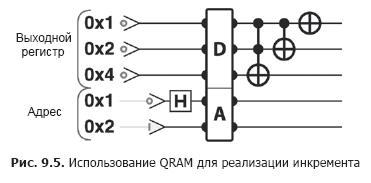
Пример кода

Этот пример можно выполнить онлайн по адресу oreilly-qc.github.io?p=9-2.
Листинг 9.2. Использование QPU для увеличения числа из QRAM — адресный регистр может содержать суперпозицию, что приведет к тому, что выходной регистр будет содержать суперпозицию хранимых значений

var a = [4, 3, 5, 1];
var reg_qubits = 3;
qc.reset(2 + reg_qubits + qram_qubits());
var qreg = qint.new(3, 'qreg');
var addr = qint.new(2, 'addr');
var qram = qram_initialize(a, reg_qubits);

qreg.write(0);
addr.write(2);
addr.hadamard(0x1);

qram_load(addr, qreg);
qreg.add(1);

Такое описание QRAM может показаться слишком неопределенным — что же собой представляет оборудование квантовой памяти? В этой книге мы не станем приводить описание того, как построить QRAM на практике (как, скажем, в большинстве книг по C++ не приводится подробное описание того, как работает традиционная память). Примеры кода вроде приведенного в листинге 9.2 выполняются с использованием упрощенной модели, имитирующей поведение QRAM. Тем не менее прототипы технологий QRAM существуют.

Хотя квантовая память будет критическим компонентом любого серьезного QPU, подробности ее реализации с большой вероятностью изменятся, как у любого квантового вычислительного устройства. Для нас важна сама идея фундаментального ресурса, который ведет себя так, как показано на рис. 9.4, и мощные приложения, которые могут быть построены на ее основе.
Имея в распоряжении квантовую память, можно переходить к построению сложных квантовых структур данных. Особый интерес представляют структуры, которые позволяют представлять векторные и матричные данные.

Кодирование векторов

Допустим, вы хотите инициализировать регистр QPU для представления простого вектора, вроде приведенного в формуле 9.1.

Формула 9.1. Пример вектора для инициализации регистра QPU.


Данные в такой форме часто встречаются в квантовых приложениях машинного обучения.
Пожалуй, самым очевидным методом кодирования векторных данных является представление каждого компонента в состоянии отдельного регистра QPU с подходящим двоичным представлением. Мы будем называть этот (вероятно, самый очевидный) метод кодированием состояния для векторов. Вектор из приведенного примера можно закодировать в четырех двухкубитных регистрах, как показано на рис. 9.6.


Одна из проблем наивного кодирования состояния заключается в том, что оно неэффективно расходует кубиты — самый драгоценный ресурс QPU. Впрочем, к плюсам традиционных векторов с кодированием состояния следует отнести то, что они не требуют квантовой памяти. Компоненты вектора можно просто сохранить в стандартной памяти и использовать их отдельные значения для управления подготовкой каждого отдельного регистра QPU. Но это преимущество также лежит в основе самого серьезного недостатка кодирования состояния векторов: хранение векторных данных таким традиционным способом не позволяет нам использовать нетрадиционные возможности QPU. Чтобы пользоваться мощью QPU, необходимо уметь манипулировать относительными фазами суперпозиций, а это непросто сделать, если каждый компонент вектора фактически рассматривает ваш квантовый процессор как набор традиционных двоичных регистров!

Вместо этого необходимо спуститься на квантовый уровень. Предположим, компоненты вектора хранятся в суперпозиции амплитуд одного регистра QPU. Так как регистр QPU из n кубитов может существовать в суперпозиции с 2n амплитудами (а следовательно, для экспериментов с круговой записью будет 2n кругов), можно представить кодирование вектора с n компонентами в регистре QPU с ceil(log(n)) кубитами.

Для примера вектора из формулы 9.1 этот подход потребует двухкубитного регистра — идея заключается в том, чтобы найти подходящую квантовую схему для кодирования векторных данных на рис. 9.7.


Назовем этот уникальный квантовый способ кодирования векторных данных комплексным амплитудным кодированием. Важно оценить различия между комплексным амплитудным кодированием и более привычным кодированием состояния. В табл. 9.1 сравниваются эти два способа кодирования для разных векторных данных. В последнем примере кодирования состояния понадобятся четыре семикубитных регистра, каждый из которых использует представление с фиксированной точкой Q7.7.

Таблица 9.1. Различия между способами кодирования векторных данных (комплексным амплитудным кодированием и кодированием состояния)


Для получения векторов с комплексным амплитудным кодированием в QCEngine можно воспользоваться удобной функцией amplitude_encode(). Программа в листинге 9.3 получает вектор значений и ссылку на регистр QPU (который должен иметь достаточный размер) и подготавливает этот регистр, выполняя комплексное амплитудное кодирование вектора.

Пример кода

Этот пример можно выполнить онлайн по адресу oreilly-qc.github.io?p=9-3.

Листинг 9.3. Подготовка векторов с комплексным амплитудным кодированием в QCEngine

// Заранее следует убедиться в том, что длина входного вектора
// равна степени 2
var vector = [-1.0, 1.0, 1.0, 5.0, 5.0, 6.0, 6.0, 6.0];

// Создать регистр достаточного размера для вектора с комплексным
// амплитудным кодированием
var num_qubits = Math.log2(vector.length);
qc.reset(num_qubits);
var amp_enc_reg = qint.new(num_qubits, 'amp_enc_reg');

// Сгенерировать комплексное амплитудное кодирование в amp_enc_reg
amplitude_encode(vector, amp_enc_reg);

В этом примере вектор просто передается в виде массива JavaScript, хранящегося в традиционной памяти, — при том что мы указали, что комплексное амплитудное кодирование зависит от QRAM. Как QCEngine выполняет комплексное амплитудное кодирование, если для программы доступна только оперативная память вашего компьютера? Хотя возможно сгенерировать схему для комплексного амплитудного кодирования и без QRAM, сделать это эффективно, безусловно, не получится. QCEngine предоставляет медленную, но работоспособную модель того, что можно достигнуть с доступом к QRAM.

Ограничения комплексного амплитудного кодирования

Поначалу идея комплексного амплитудного кодирования выглядит отлично — оно использует меньше кубитов и предоставляет квантовые средства для работы с векторными данными. В любом приложении, в котором используется этот механизм, необходимо учитывать два важных фактора.

Проблема 1: квантовые результаты

Возможно, вы уже обратили внимание на первое из этих ограничений: квантовые суперпозиции в общем случае не могут читаться операцией READ. Снова наш главный противник! Если распределить компоненты вектора по квантовой суперпозиции, их не удастся прочитать снова. Естественно, это не создает особых проблем при передаче векторных данных на вход другой программы QPU из памяти. Но очень часто приложения для QPU, получающие векторные данные с комплексным амплитудным кодированием на входе, также генерируют векторные данные с комплексным амплитудным кодированием на выходе.

Таким образом, применение комплексного амплитудного кодирования жестко ограничивает нашу возможность чтения выходных данных приложений операцией READ. К счастью, из результатов с комплексным амплитудным кодированием часто возможно извлечь полезную информацию. Как будет показано в следующих главах, хотя вы не можете узнать отдельные компоненты, можно узнать глобальные свойства векторов, закодированных таким способом. Тем не менее комплексное амплитудное кодирование — не панацея, и его успешное применение требует внимания и изобретательности.

Проблема 2: требование нормировки векторов

Вторая проблема, связанная с комплексным амплитудным кодированием, скрыта в табл. 9.1. Присмотритесь повнимательнее к комплексному амплитудному кодированию первых двух векторов в таблице: [0,1,2,3] и [6,1,1,4]. Могут ли комплексные амплитуды двухкубитного регистра QPU принять значения [0,1,2,3] или значения [6,1,1,4]? К сожалению, нет. В предыдущих главах мы обычно обходили обсуждение амплитуд и относительных фаз в пользу более интуитивной круговой записи. Хотя такой подход был более интуитивным, он оградил вас от одного важного числового правила, касающегося комплексных амплитуд: квадраты комплексных амплитуд регистра должны в сумме давать 1. Это требование, называемое нормировкой, выглядит логично, если вспомнить, что квадраты амплитуд в регистре соответствуют вероятностям чтения различных результатов. Так как должен быть получен один какой-то результат, эти вероятности (а следовательно, и квадраты всех комплексных амплитуд) должны в сумме давать 1. При использовании удобной круговой записи легко забыть о нормировке, но она устанавливает важное ограничение на то, к каким векторным данным может применяться комплексное амплитудное кодирование. Законы физики не позволяют создать регистр, находящийся в суперпозиции с комплексными амплитудами [0,1,2,3] или [6,1,1,4].

Чтобы применить комплексное амплитудное кодирование к двум проблемным векторам из табл. 9.1, сначала необходимо их нормировать, разделив каждый компонент на сумму квадратов всех компонентов. Например, при комплексном амплитудном кодировании вектора [0,1,2,3] сначала необходимо разделить все компоненты на 3,74 для получения нормированного вектора [0.00, 0.27, 0.53, 0.80], который теперь подходит для кодирования в комплексных амплитудах суперпозиции.

Имеет ли нормировка векторных данных какие-либо нежелательные эффекты? Все выглядит так, словно данные полностью изменились! На самом деле нормировка оставляет большую часть важной информации без изменений (в геометрическом представлении она всего лишь масштабирует длину вектора, оставляя направление без изменений). Можно ли считать, что нормализованные данные полностью заменяют исходные? Это зависит от потребностей конкретного приложения QPU, в котором вы собираетесь их использовать. Помните, что при необходимости числовое значение коэффициента нормализации можно хранить в другом регистре.

Комплексное амплитудное кодирование и круговая запись

Когда вы начинаете более конкретно думать о числовых значениях комплексных амплитуд регистров, будет полезно напомнить себе, как комплексные амплитуды представляются в круговой записи, и заметить возможную ловушку. Заполненные области в круговой записи представляют квадраты амплитуд комплексных амплитуд квантового состояния. В таких ситуациях, как при комплексном амплитудном кодировании, когда комплексные амплитуды должны представлять компоненты вектора с вещественными значениями, это означает, что заполненные области определяются квадратом соответствующего компонента вектора, а не самим компонентом. На рис. 9.8 показано, как правильно интерпретировать представление вектора [0,1,2,3] после нормализации в круговой записи.


Теперь вы знаете о векторах с комплексным амплитудным кодированием достаточно, чтобы разобраться в приложениях для QPU, которые будут приведены в книге. Но для многих приложений, особенно относящихся к области квантового машинного обучения, необходимо пойти на шаг дальше и использовать QPU для манипуляций не только с векторами, но и с целыми матрицами данных. Как же закодировать двумерные массивы чисел?

» Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок

Для Хаброжителей скидка 25% по купону — Programming

По факту оплаты бумажной версии книги на e-mail высылается электронная книга.