Сегодняшняя статья будет посвящена сразу двум нашим любимым темам: компьютерной томографии (КТ) и отечественному процессору Эльбрус. Мы расскажем, чем отличается рентгенограмма от результатов КТ и объясним, зачем такой большой и серьезной машине, как томограф, был бы кстати специализированный вычислитель. Несмотря на то, что томографы используются уже почти 50 лет (создание первого томографа было анонсировано в 1972 году [1]), это не означает, что все проблемы KT сегодня решены. Наоборот, существует острая потребность в новых томографических алгоритмах, которые были бы быстрее и точнее используемых, позволили бы уменьшить лучевую нагрузку на объект, что, в свою очередь, существенно расширило бы и сферу применения метода КТ. Понимая все это, мы создали такое программное обеспечение Smart Tomo Engine. О нем речь пойдет ниже. Рассказав ранее о борьбе с ортотропными артефактами и об оценке “эффекта чаши”, в данной статье мы опишем несколько тестов, проведенных с использованием синтетических и собранных на отечественном томографе реальных томографических датасетах и покажем работу нашей программы на процессоре Эльбрус нового поколения (видео прилагается ниже). Результат работы программы приоткроет внутренний мир майского жука, причем значение слова “внутренний” здесь следует понимать буквально.

Рентгенография — широко используемый метод неинвазивной диагностики, основанный на формировании изображения объекта с помощью рентгеновского излучения. Для этого исследуемый объект помещается между источником рентгеновского излучения и регистратором (рис. 1 слева). В качестве регистратора может выступить рентгеночувствительная пленка или позиционно-чувствительный детектор. Изображение формируется прошедшим через объект и ослабленным при своем прохождении излучением. Разные материалы ослабляют рентгеновское излучение по-разному, что обеспечивает контраст на изображении. Регистрируя прошедшее через объект рентгеновское излучение, можно судить о локальном составе исследуемого объекта. Пример рентгенограммы грудной клетки показан на рис. 1 справа. Здесь светлые области характеризуют участки большего поглощения. Рассматривая ребра (светлые изогнутые пластинки), ограничивающие грудную клетку (темная полость с просматриваемыми светлыми участками бронхиального дерева), в верхней части грудины (центральный светлый столб) с правой стороны мы видим небольшое светлое утолщение.

Рис. 1. Рентгенография: принципиальная схема (слева); результат рентгеновского исследования — рентгенограмма (справа). Источник.
Рентгенография не позволяет понять, на какой глубине находится проблемная часть — прямо на грудине, перед ней или за ней. По одной проекции трудно не только проанализировать тонкую пространственную структуру проблемной части, но и определить ее общую форму. На рис. 2 данный факт и проиллюстрирован.

Рис.2. Источник.
Уточнить форму и внутреннее строение поможет метод КТ. Также как и в рентгенографии, для сбора данных КТ объект помещается между источником рентгеновского излучения и детектором, но регистрируется уже набор рентгенограмм под разными углами. Углы поворота обычно равномерно распределены в некотором интервале. Принципиальная схема измерения показана на рис. 3.

Рис. 3. Принципиальная схема томографической съемки (источник).
Сбор изображений под разными углами проводится на специальном приборе — томографе. Поскольку томографироваться могут самые разные объекты живой и неживой природы, а исследования проводятся и на микро-, и макро- уровнях, то разновидностей томографов огромное число. Они отличаются схемами сканирования (послойно-круговая, спиральная и т.д.), используемыми типами источников излучения, схемами формирования зондирующего пучка (конусная, параллельная, микрофокусная). В самых общих чертах схему томографа можно представить так: источник излучения, держатель объекта исследования и детектор. Подвижной частью, позволяющей контролируемо менять ракурс съемки, может быть любая из трех частей. Современный томограф также немыслим без компьютера, который не только управляет схемой сбора рентгенограмм, но производит обработку собранных данных с помощью специализированного ПО.
Для исследования объектов разной природы могут использоваться принципиально отличающиеся друг от друга технические решения. Так, при медицинских исследованиях гентри (подвижное устройство, содержащее систему детекторов и рентгеновских излучателей) (Рис. 4) вращается вокруг неподвижного пациента. Пространственное разрешение в таких томографах достигает 0.2-0.5 мм. Результаты КТ сохраняются в формате DICOM — медицинском отраслевом стандарте, разработанном для создания, хранения, передачи цифровых медицинских изображений и сопутствующих документов обследованного пациента.

Рис. 4. Схема медицинского томографа (источник).
Для научных исследований in vitro, проводимых в лабораторных условиях, применяется другая экспериментальная схема — источник и детектор неподвижны, а набор рентгенограмм получают, вращая образец. Во ФНИЦ “Кристаллография и фотоника” РАН (ФНИЦ КФ РАН) в лаборатории рефлектометрии и малоуглового рассеяния был сконструирован и функционирует целый комплекс лабораторных рентгеновских микротомографов. Изображение одного из созданных приборов представлено на рис. 5. В нем образец размещается на гониометре, ось которого перпендикулярна направлению зондирования. Прибор оборудован двумерным детектором. Размер пикселя — 9 мкм, поле зрения детектора — 24 на 36 мм. В данном приборе реализована возможность использования для зондирования как полихроматического, так и монохроматического излучения. Это позволяет не только повышать качество реконструируемых изображений, но и получать дополнительную информацию об элементном составе изучаемых объектов. Разработка собственных томографов позволяет получить доступ к экспериментальным данным (рентгенограммам) и параметрам работы всех узлов томографа, а, значит, позволяет оптимизировать протоколы измерений в зависимости от поставленных задач.

Рис. 5. Фотография лабораторного микротомографа ФНИЦ КФ РАН.
После регистрации рентгенограмм под разными углами, т.е. сбора полного набора проекций, начинается их обработка. Финальная цель обработки — восстановление внутренней морфологической структуры объекта. Поскольку контраст на регистрируемом изображении формируется за счет способности разных материалов по-разному ослаблять рентгеновское излучение, то результатом реконструкции является пространственное распределение коэффициентов ослабления зондирующего излучения. На это распределение и опирается описание морфологической структуры томографируемых объектов.
Если зондирование проводится с использованием параллельного пучка, то задачу трехмерной реконструкции можно решить, восстановив серию двумерных сечений объекта. Для реконструкции одного сечения нет необходимости использовать полный набор проекций. Требуется лишь одна строка фиксированного номера от каждой угловой проекции. Все эти строки соответствуют одному горизонтальному сечению восстанавливаемого 3D распределения, которому можно приписать тот же номер. На рис. 6 слева представлено изображение, собранное из таких строк. Горизонтальная ось отвечает за номер столбца детектора, вертикальная — за номер углового поворота. Справа на рис. 6 приведен результат реконструкции сечения.
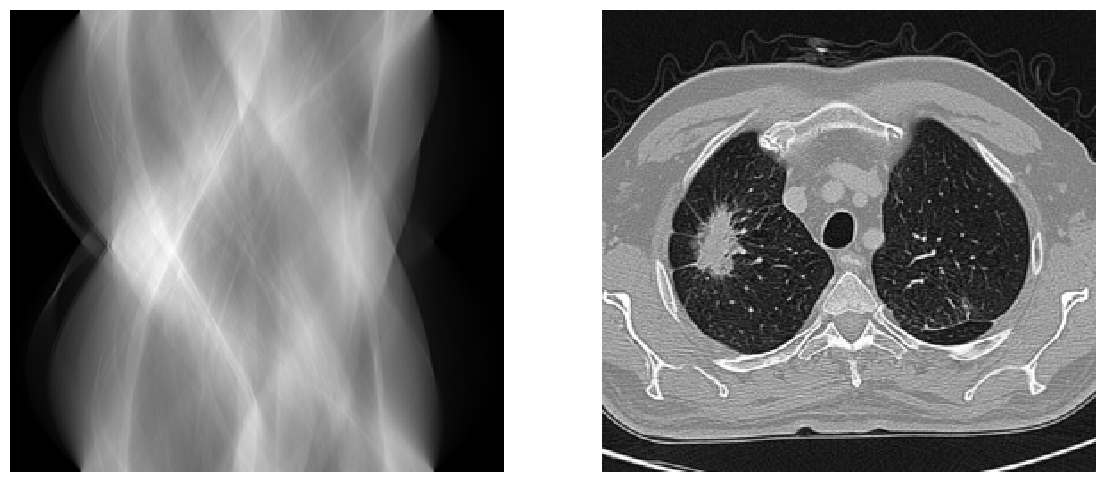
Рис 6. Синограмма грудной клетки (слева); результат КТ — сечение 3D изображения (справа).
Если для томографического зондирования используется монохроматическое рентгеновское излучение, то, опираясь на закон Бугера-Ламберта-Бера, задачу реконструкции можно свести к задаче обращения преобразования Радона. Преобразование Радона — это интегральное преобразование, которое связывает значения функции со значениями ее интегралов по всевозможным прямым. Процедура обращения — это восстановление неизвестной функции по известным значениям ее интегралов по прямым. Подынтегральная функция, которую и надо восстановить — это распределение линейного коэффициента ослабления монохроматического рентгеновского излучения в объеме образца. Свойство обратимости преобразования Радона гарантирует точное восстановление неизвестной частотно-ограниченной функции при наличии достаточного числа интегралов по регулярно расположенным прямым. Это свойство использует алгоритм свертки и обратной проекции (Filtered Back Projection, FBP), реализованный в большинстве современных серийных томографов. Он состоит из двух шагов. Первый шаг — линейная фильтрация зарегистрированных изображений. Второй шаг — обратное проецирование, т.е. равномерное “размазывание” каждой полученной на предыдущем шаге одномерной функции по соответствующему направлению на все двумерное изображение с последующей суммацией. Результат работы алгоритма — восстановленное пространственное распределение линейного коэффициента ослабления рентгеновского излучения заданной энергии. Если зондирование ведется не параллельным, а конусным пучком, то послойную реконструкцию организовать не удается, и приходится использовать более сложные алгоритмы. Об алгоритмах трехмерной реконструкции, например об алгоритме Фельдкампа, мы напишем как-нибудь в следующий раз. А теперь перейдем, наконец, к описанию нашего ПО.
Smart Tomo Engine
Сердцем Smart Tomo Engine служит библиотека томографической реконструкции, предоставляющая через API следующие функции: чтение томографических изображений (проекций); собственно томографическую реконструкцию (предлагается на выбор три алгоритма) и сохранение результатов (предлагаемые форматы: DICOM, PNG). Программный продукт дополнительно включает в себя графический интерфейс пользователя, обеспечивающий двухмерную визуализацию томографических изображений и результатов реконструкции. Основное назначение программного продукта — выполнение реконструкции трехмерного цифрового изображения объекта по набору его трансмиссионных томографических изображений в рентгеновском диапазоне.
Для послойной двумерной реконструкции реализованы следующие алгоритмы:
- FBP — Filtered Back Projection. Классический метод томографической реконструкции, комбинирующий обратное проецирование и линейную фильтрацию. Вычислительная сложность O(n3). Подробнее о методе можно почитать в [2]).
- DFR — Direct Fourier Reconstruction. Алгоритм работает в частотной области и использует быстрое преобразование Фурье для фильтрации и обратного проецирования [3]. Вычислительная сложность O(n2 log n) операций умножений.
- HFBP — Hough FBP. Алгоритм реконструкции, который разработали наши ученые. Для обратного проецирования используется алгоритм Брейди быстрого вычисления преобразования Хафа, а для ускорения линейной фильтрации применяется метод Дериша [4,5]. Вычислительная сложность по сравнению с DFR снижена до O(n2) операций умножения (при O(n2 log n) операций сложения).
Тестирование на Эльбрус
Мы протестировали наше ПО на отечественной платформе. Тестирование проводилось на машинах Эльбрус-401, Эльбрус-804 и Эльбрус-801СВ. Эльбрус-401 — это рабочая станция с процессором Эльбрус-4С, Эльбрус-804 — сервер с 4 процессорами Эльбрус-8С. (Мы уже тестировали на них наше ПО, разработанное для решения других задач, и почитать про это можно, например, тут.) Эльбрус-801СВ — это новейшая разработка МЦСТ: рабочая станция с процессором Эльбрус-8СВ. Про принципиальные отличия Эльбрусов разных поколений нам рассказали коллеги из МЦСТ: “Эльбрус-4С – первый процессор, массово поставленный на рынок. Имеет 4 ядра с частотой 750…800 МГЦ, 3 канала памяти DDR3-1600. Эльбрус-8С – 8 ядер, частота 1.2…1.3 ГГц, 4 канала памяти DDR3-1600, и при этом – в каждом ядре в 1.5 раза больше исполнительных устройств (ALU) для вычислений с плавающей запятой. Эльбрус-8СВ – дальнейшее улучшение: 8 ядер с частотой 1.5 ГГц, память DDR4-2400 и ещё в 2 раза больше ALU. Эльбрус-8СВ лучше работает с невыровненными данными, и в нём масса других небольших улучшений по сравнению с Эльбрус-8С”.
Характеристики процессоров представлены в таблице 1.
Таблица 1. Технические характеристик использованных процессоров.
| Эльбрус-4C, 800 МГц | Эльбрус-8C, 1200 МГц | Эльбрус-8СВ, 1500 МГц | AMD Ryzen 7 2700 | AMD Ryzen Threadripper 3970X | |
|---|---|---|---|---|---|
| Тактовая частота, МГц | 800 | 1200...1300 | 1500 | 3200 | 3700 |
| Число ядер | 4 | 8 | 8 | 8 | 32 |
| Число операций за такт (на ядро) | до 23 | до 25 | до 50 | – | – |
| L1 кэш, на ядро (данные) | 64 Кб | 64 Кб | 64 Кб | 32 Кб | 32 Кб |
| L1 кэш, на ядро (команды) | 128 Кб | 128 Кб | 128 Кб | 64 Кб | 32 Кб |
| L2 кэш, на ядро | 2 Mб | 512 Кб | 512 Кб | 512 Кб | 512 Кб |
| L3 кэш, общая | – | 16 Мб | 16 Мб | 16 Мб | 128 Мб |
| Организация оперативной памяти | До 3 каналов DDR3-1600 ECC | До 4 каналов DDR3-1600 ECC | До 4 каналов DDR4-2400 ECC | До 2 каналов DDR4-2933 ECC | До 4 каналов DDR4-3200 ECC |
| Технологический процесс | 65 нм | 28 нм | 28 нм | 12 нм | 7 нм |
| Количество транзисторов | 986 млн. | 2,73 млрд. | 3,5 млрд. | 4,8 млрд. | 23,54 млрд. |
| Максимальная ширина SIMD инструкции | 64 бита | 64 бита | 128 бит | 256 бит | 256 бит |
| Поддержка многопроцессорных систем | до 4 проц. | до 4 проц. | до 4 проц. | ? | ? |
| Год начала производства | 2014 | 2016 | 2019 | 2018 | 2019 |
| Операционная система | ОС “Эльбрус” 5.0-rc2 | ОС “Эльбрус” 6.0-rc1 | ОС “Эльбрус” 6.0-rc1 | Ubuntu 18.04 | Archlinux |
| Версия компилятора | lcc 1.24.09 | lcc 1.25.07 | lcc 1.25.05 | gcc 7.5.0 | gcc 10.1.0 |
Про оптимизацию на платформе Эльбрус мы уже писали тут и тут, поэтому не будем повторяться. Здесь мы не делали ничего сверхъестественного:
- использовали оптимизированную библиотеку EML (геометрические преобразования изображения (напр., аффинное преобразование), арифметические операции и т.д.);
- использовали интринсики там, где EML не смогла нам помочь; однако на Эльбрус-8СВ SIMD стал 128-битным, и мы не успели полностью на него перейти, поэтому интринсики все еще работали с 64-битными векторами.
Для тестирования Smart Tomo Engine мы собрали два датасета: с синтетическими и реальными данными. Синтетический датасет “Шепп-Логан 3D” был получен методом математического моделирования. Проекции рассчитаны послойно от трехмерного фантома Шеппа-Логана с использованием веерной схемы. Срез представлен на рис. 8 слева. Размер изображения фантома 511х511х511. Проекции рассчитаны для 420 углов, равномерно распределенных от 0.5 до 210 градусов. В эксперименте на вход Smart Tomo Engine подавалось 511 синограмм (изображение одной из них приведено на рис. 7 справа) размером 511х420. Выход — 511 реконструированных слоев, размер каждого слоя 511х511. Размер фантома примерно соответствует изображениям, получаемым на современных стоматологических томографах: максимальный размер зоны сканирования челюсти обычно составляет 16 см, заявляемое производителями пространственное разрешение — 0.3-0.4 мм. В таком случае размер регистрируемой проекции составит примерно 500х500 пикселей.

Рис. 7. Слева — срез трехмерного фантома Шеппа-Логана, справа — синограмма центрального слоя.
Реальные томографические данные (датасет "Майский жук") были собраны на микротомографе ФНИЦ КФ РАН, предназначенном для проведения научных исследований. Размер пикселя использованного детектора составлял 9 микрон. Экспериментальный образец — высушенный майский жук. Было снято 400 проекций в параллельной схеме. Образец, закрепленный на держателе, поворачивался на углы в диапазоне от 0.5 до 200 градусов с шагом 0.5 градусов. Время измерения одной проекции составило 5 секунд. Размер измеренной проекции — 1261х1175. Вход для Smart Tomo Engine — 1261 синограмма размером 1175х400, выход — 1261 восстановленный слой размера 1175х1175.
А теперь самое интересное — результаты замеров и выводы
На этих датасетах мы провели замеры скорости выполнения реализованных нами алгоритмов реконструкции: FBP, DFR и HFBP. Время работы алгоритмов приведено в таблице 2. Замеры проводились на 5 машинах: Эльбрусе-401, Эльбрусе-804, Эльбрусе-801СВ, AMD Ryzen 7 2700 и AMD Ryzen Threadripper 3970X. Для каждой машины в таблице указано число процессоров, число физических ядер и максимальное число одновременно выполняемых потоков (указано в скобках). Замеры скорости реконструкции проводились в двух режимах: однопоточном (1П) и многопоточном (МП), реализованном с помощью библиотеки tbb версии “2017 update 7”.
Таблица 2. Замеры времени работы программы, сек.
| Архитектура | Эльбрус | x86_64 (AMD Ryzen) | ||||||||
| Модель | 4С(800MHz) | 8С(1200MHz) | 8СВ(1500MHz) | 7 2700 | Threadripper 3970X | |||||
| Процессоры х ядра (потоки) | 1 x 4(4) | 4 x 8(8) | 1 x 8(8) | 1 x 8(16) | 1 x 32(64) | |||||
| Режим | 1П | 4П | 1П | 32П | 1П | 8П | 1П | 16П | 1П | 64П |
| Алгоритм | Время работы, с | |||||||||
| Датасет «Шепп-Логан 3D» (511 слоёв) | ||||||||||
| FBP | 959 | 271 | 569 | 31 | 514 | 85 | 213 | 52 | 237 | 19 |
| DFR | 853 | 234 | 546 | 23 | 497 | 69 | 60 | 10.5 | 61 | 5.1 |
| HFBP | 760 | 200 | 496 | 19 | 406 | 55 | 46 | 8.3 | 42 | 2.3 |
| Датасет «Майский жук » (1261 слой) | ||||||||||
| FBP | 17755 | 6593 | 8845 | 685 | 8342 | 1992 | 4789 | 1061 | 4326 | 568 |
| DFR | 9910 | 2847 | 6351 | 236 | 5575 | 733 | 771 | 141 | 724 | 77 |
| HFBP | 9075 | 2419 | 5512 | 189 | 4540 | 597 | 578 | 97 | 579 | 41 |
Анализируя полученные результаты, прежде всего отметим, что в многопоточном режиме 4-процессорный сервер Эльбрус-804 затратил на реконструкцию 511 слоев фантома алгоритмом HFBP 19 секунд, то есть каждый слой был восстановлен за 0.037 секунды, а послойная частота составила 26.8 слоев в секунду (26.8 ips). Чтобы понять, высокая это частота или низкая, приведем следующую оценку. За секунду гентри 16-срезового кардиологического томографа совершает чуть меньше двух оборотов, регистрируя порядка 30 синограмм. Мы восстанавливаем 26.8 слоя в секунду, т.е. проводим реконструкцию практически в режиме реального времени. Таким образом, проведение реконструкции с использованием российской платформы удовлетворяет требованиям по скорости, предъявляемым в кардиологии, где основным реперным параметром является период сокращения сердца, который в среднем составляет одну секунду.
Реконструкция в реальном времени требуется также для реализации нового протокола сканирования, предложенного недавно нашими учеными — контролируемой реконструкции [6]. Использование этого протокола уменьшает лучевую нагрузку за счет того, что сбор рентгенограмм прерывается сразу, как только их набор оказывается достаточным для восстановления.
Для научных исследований таких жестких ограничений по времени нет, но выше требования к пространственному разрешению. Поэтому размеры восстанавливаемых сечений — больше. При работе с датасетом, полученным с лабораторного микротомографа, на реконструкцию 1261 слоя потребовалось 189 секунды в многопоточном режиме (6.7 ips). Измерение входных данных на лабораторном томографе заняло 2000 секунд, а 3 с небольшим минуты, которые потребовались на реконструкцию всех слоев при использовании Smart Tomo Engine на Эльбрусе-804, соответствуют 10% этого времени. Ещё быстрее будет работать 4-процессорный сервер с процессором Эльбрус-8СВ, который в МЦСТ уже разработали и скоро планируют довести до готовности к серийному производству.
В полученных результатах интересны и сами по себе соотношения производительностей разных платформ на каждом из алгоритмов, с учётом тактовой частоты ядер. На FBP отставание Эльбрусов умеренное, и при нормировании относительно тактовой частоты получаются близкие результаты. Но на алгоритмах DFR и HFBP отставание всех Эльбрусов от платформы х86 значительно больше. Почему? Ответ кроется в недостаточной оптимизации нашего ПО под платформу Эльбрус, все же на x86_64 мы потратили 5 лет, а под Эльбрус, особенно под 8СВ, большую часть программ и алгоритмов мы еще вовсе не оптимизировали.
В ближайшее время мы планируем ускорения в трех направлениях. Первое, что мы сделаем, — это оптимизируем наши вычисления на интринсиках. Сейчас наши вычисления сделаны для 64-битного SIMD, а у Эльбрус-8СВ SIMD стал 128-битным. Второе ускорение будет сделано командой МЦСТ. Уже сейчас ведутся разработки для поддержки двумерного и одномерного дискретного преобразования Фурье для входного вектора, размер которого не равен степени двойки. И так как пока его нет, мы пользовались библиотекой ffts, с некоторой доработкой как под Эльбрус, так и под х86.
Для оценки возможного ускорения нашей программы мы сделали замеры времени выполнения дискретного преобразования Фурье на процессоре Эльбрус-8СВ для входной комплексной матрицы размером 512 на 512. Неоптимизированная на Эльбрус библиотека ffts выполнила эту операцию за 27 миллисекунд, а eml справилась всего за 5.5. Мы ускорили, как могли, ffts с помощью вызовов EML в 2 раза, и в таблице 2 замеры проведены уже с учётом этой оптимизации. Таким образом, если оптимизацию проводить с той тщательностью, с которой сделана библиотека eml, то алгоритм DFR на Эльбрусе все еще может быть ускорен почти в 2,5 раза.
Третье, но не менее важное ускорение относится к алгоритму HFBP, который основан на применении преобразования Хафа. Данное преобразование также пока еще не представлено в библиотеке eml, а наша версия оптимизирована только с помощью векторных операций. И, так как данный алгоритм вычислительно эффективнее, чем DFR, наши теоретические выводы и оптимизированная под платформу x86_64 версия это показывают, то данный алгоритм тоже может быть ускорен еще в несколько раз. О результатах этих оптимизаций мы обязательно расскажем в следующий раз.
А вот и обещанное видео с работой программы на Эльбрус-8СВ.
Вот такой внутренний мир майского жука у нас получился.
Заключение
В статье мы представили вам нашу новую разработку — программное обеспечение для томографической реконструкции Smart Tomo Engine, которое:
- включает в себя инновационный алгоритм HFBP, стабильно обгоняющий по производительности лидера прошлых лет DFR;
- поддерживает операционные системы: ОС Эльбрус, MS Windows, macOS, различные дистрибутивы Linux;
- поддерживает процессорные архитектуры: Эльбрус, x86, x86_64;
- является полностью отечественной разработкой;
- в составе программно-аппаратного комплекса на платформе Эльбрус подходит для медицинских и промышленных сканеров всех поколений, для новейших нано-томографов (приборов, которые реконструируют объекты с субмикронным разрешением), а также синхротронных центров.
Ну а главный результат этой статьи заключается в том, что комбинации отечественного процессора Эльбрус и Smart Tomo Engine достаточно для томографии в реальном времени, даже без дополнительных ускорений, работа над которыми уже ведется!
P.S. А еще мы не смогли удержаться и замерили производительность UNet’а на Эльбрусе. UNet — популярная нейросетевая архитектура для решения задач сегментации. Изначально Unet была разработана для решения задачи сегментации в медицине, а по обработанным этим нейросетевым подходом томографическим снимкам теперь определяют патологии и новообразования. Вычислительно тяжелые части нейронных сетей у нас реализованы на EML, а EML оптимизировано под разные поколения Эльбрусов, поэтому на таком замере можно лучше оценить реальную производительность разных процессоров. Замеры выполнены для одного ядра, без распараллеливания, чтобы не оглядываться на число ядер.
| Эльбрус-4C, 800 МГц | Эльбрус-8C, 1200 МГц | Эльбрус-8СВ, 1500 МГц | AMD Ryzen Threadripper 3970X, 3700 (до 4500) МГц | |
|---|---|---|---|---|
| UNet, вход 256 на 256 | 4,45 c | 2,45 c | 0,81 с | 0,61 c |
Обратите внимание на последние две цифры. Круто?.. А наши исследования продолжаются...
- https://en.wikipedia.org/wiki/History_of_computed_tomography
- A. C. Kak, M. Slaney, G. Wang. "Principles of computerized tomographic imaging", Medical Physics, 2002, vol. 29, №1, pp. 107-107.
- F. Natterer. "Fourier reconstruction in tomography", Numerische Mathematik, 1985, vol. 47, №3, pp. 343-353.
- A. Dolmatova, M. Chukalina and D. Nikolaev. "Accelerated fbp for Computed tomography image reconstruction", IEEE ICIP 2020, Washington, DC, United States, IEEE Computer Society, 2020, to be published.
- А. В. Долматова, Д. П. Николаев. "Ускорение свертки и обратного проецирования при реконструкции томографических изображений", Сенсорные системы, 2020, Т. 34, №1, c. 64-71, doi: 10.31857/S0235009220010072.
- K. Bulatov, M. Chukalina, A. Buzmakov, D. Nikolaev and V. V. Arlazarov, "Monitored Reconstruction: Computed Tomography as an Anytime Algorithm", IEEE Access, 2020, vol. 8, pp. 110759-110774, doi: 10.1109/ACCESS.2020.3002019.


Alexufo
Здорово. А для задачи восстановления проекционных изображений могут ли использоваться мощности графических карт? Вроде бы есть библиотеки для FFT. developer.nvidia.com/cufft
SmartEngines Автор
Реализации томографической реконструкции на видеокартах, конечно, уже существуют. И на суперкомпьютерах — тоже. Однако цель нашей статьи — рассказать об алгоритмах, обеспечивающих восстановление в реальном времени на процессорах общего назначения.
Civil
А зачем ограничиваться процессорами общего назначения, если есть видеокарты, которые скорее всего намного лучше подходят для этих задач?
SmartEngines Автор
Решая задачу с ограничениями, инженер создает продукт, обладающий конкурентными преимуществами. Инженеры производителей видеокарт работают в условиях жестких ограничений и упаковывают громадное количество АЛУ в единицу площади кремниевой пластины. Их бизнес процветает. Мы работаем с другим типом ограничений — наши продукты должны работать, по возможности, на любых платформах. Это тоже действует. А работая без ограничений ничего инновационного создать нельзя.
Civil
Не понимаю связь «любой платформы» с «только на CPU».
Мне как не сведующему в томографии человеку кажется, что если у вас вычислительно-интенсивная задача и требование скорости, то логично делать рассчеты на видеокартах. Я не вижу при этом чтобы это накладывало принципиальные ограничения на платформу, даже наоборот, кажется что будь все это сделано на OpenCL можно было бы поддерживать еще большее их число и сразу оптимально (просто требовать наличия поддержки OpenCL платформой или наличие PCIe шины куда можно воткнуть какой-нибудь FirePro) без необходимости делать архитектурно-специфические оптимизации. Но да, придется делать оптимизации под различные видеокарты, что тоже в общем-то ограничение, просто другое.
SmartEngines Автор
В ужасе мы перечитали статью и комментарии. И с облегчением обнаружили, что нигде не было заявлено про «только на CPU». Мы работаем и на GPU. Наши алгоритмы хорошо параллелизуются на векторных архитектурах. Но писать тут не о чем — это технологический мэйнстрим. Вот когда появится отечественный GPU — будет, о чем написать. Или вот: мы планируем освоить еще и NPU. Как осилим — обязательно напишем, это должно быть любопытно. А на OpenCL мы возлагали очень большие надежды. Думали, что можно будет одинаково абстрагировать CPU и GPU. Но в прошлом, 2019 году он выглядел как дохлая лошадь. В этом году движение возобновилось, и мы внимательно наблюдаем, появятся ли стабильные реализации на достаточном числе платформ. Тогда и решим.
lelik363
Модуль МС127.05 тоже пробовали?
SmartEngines Автор
Пока нет, но в ближайших планах научится с ним работать в наших задачах и не только по томографии.
LittleAlien
Тогда непонятно, как можно хвалиться визуализацией, которая работает несколько секунд (второе видео в материале) вместо реального времени на GPU.
Для сравнения, 2015-й год и слабая ноутбучная видеокарта:
www.youtube.com/watch?v=d9I9OoqHK2o
SmartEngines Автор
Присланное видео и наша визуализация — это не об одном и том же. Цель нашей визуализации — мониторинг процесса реконструкции (показан на первом ролике). Цель присланного видео — показать возможности программы визуализации.
Второй же наш ролик сделан для красивой демонстрации результата реконструкции, полученного с помощью Smart Tomo Engine, скорость визуализации задана из наших представлений о прекрасном и наглядности результата.
LittleAlien
Я понимаю, что это две отдельные задачи, реконструкция и визуализация. Я хотел сказать (и подтвердить предположение Civil), что GPU здесь в целом подходят лучше, так как могут делать и реконструкцию, и визуализацию в реальном времени.
Сравнить скорость отрисовки на GPU и CPU можно например в этой софтине:
ngavrilov.ru/invols/index.php?id=Download
SmartEngines Автор
Для отрисовки, однозначно, лучше всего подходят GPU — они для этого созданы. А вот для вычислений все зависит от алгоритмов(упс) и часть алгоритмов хорошо «ложится» на GPU, а многие совсем нет. В своих работах мы используем ресурсы GPU, по мере необходимости и если это эффективно. Но ориентироваться только на них мы считаем глупостью.
LittleAlien
Отрисовка КТ на GPU, кстати, совсем не похожа на полигональную графику в играх, так что «для этого созданы» не совсем верно.