Два специалиста по информатике нашли в весьма неожиданном месте идею, которая как раз пригодилась им для прорыва в теории графов

В октябре 2019 Якоб Хольм и Ева Ротенберг пролистывали работу, опубликованную ими за несколько месяцев до этого – и вдруг поняли, что наткнулись на нечто серьёзное.

Десятилетиями специалисты по информатике пытались разработать быстрый алгоритм для определения того, можно ли добавить к определённому графу рёбра так, чтобы он остался «планарным» – то есть, чтобы его рёбра не пересекались. Однако ни у кого не получалось улучшить алгоритм, опубликованный более 20 лет назад.

Хольм и Ротенберг с удивлением обнаружили, что в их работе есть идея, позволявшая достаточно сильно улучшить этот алгоритм. Она «разобралась с одним из главных препятствий на пути к реальному алгоритму», — сказал Хольм, специалист по информатике из Копенгагенского университета. «Возможно, мы полностью раскрыли этот вопрос».

Парочка поспешила приступить к работе над новой статьёй. Они представили её в июне на симпозиуме по вычислительной теории, проводимом Ассоциацией вычислительной техники, где подробно описали метод проверки графа на планарность, превосходящий предыдущий вариант экспоненциально.

«Новый алгоритм устроен поистине мастерски», — сказал Джузеппе Италиано, специалист по информатике из Луисского университета, соавтора работы от 1996 года, где описывается уже теперь второй по скорости алгоритм. «Когда я участвовал в написании той работы, я не думал, что такое может случиться».

Графы – это наборы вершин, соединённых рёбрами. С их помощью можно обозначать всё – от социальных сетей до дорожных сетей и электрических проводников на плате. Если в последнем случае граф не будет планарным, то два проводника пересекут друг друга, что приведёт к короткому замыканию.

Ещё в 1913 году планарные графы появились в сложной «коммунальной» задачке про три домика, опубликованной в журнале The Strand Magazine. Издание попросило читателей проложить коммуникации для трёх домов, соединяющие каждый из них с тремя энергоносителями – водой, газом и электричеством – так, чтобы коммуникации не пересекались друг с другом. Не нужно много времени, чтобы понять, что эта задача неразрешима.

Однако в случаях с более сложными графами не всегда очевидно, являются ли они планарными. Ещё сложнее сказать, останется ли сложный граф планарным, когда вы начнёте добавлять к нему рёбра – как бывает при планировке новых дорог.

Специалисты по информатике давно ищут алгоритм, способный быстро определить, можно ли внести нужное изменение так, чтобы граф оставался планарным, не перебирая при этом каждую из частей графа, когда изменениям подвергается лишь малая его часть. Алгоритму от 1996 года требовалось для этого количество шагов, примерно пропорциональное квадратному корню от количества вершин графа.

«Это гораздо лучше, чем каждый раз проверять всё с нуля, но не идеально», — сказал Хольм.

Новый алгоритм проверяет планарность за количество шагов, пропорциональное кубу логарифма от количества вершин графа – улучшение получается экспоненциальным. Хольм и Ротенберг из Датского технического университета достигли этого ускорения, воспользовавшись преимуществом особого свойства планарных графов, открытого ими в прошлом году.

Чтобы понять их метод, сначала нужно отметить, что один и тот же планарный граф можно рисовать по-разному. Все связи этих вариантов остаются одинаковыми, однако рёбра могут располагаться относительно друг друга по-разному.

К примеру, рисунок А можно поменять на рисунок В, перевернув треугольник, который составляют вершины 1,2 и 3 относительно ребра, соединяющего вершины 2 и 3. Верхнюю часть рисунка В также можно отразить относительно вершин 4 и 5, получив рисунок С. Рисунки выглядят по-разному, но обозначают один и тот же граф.



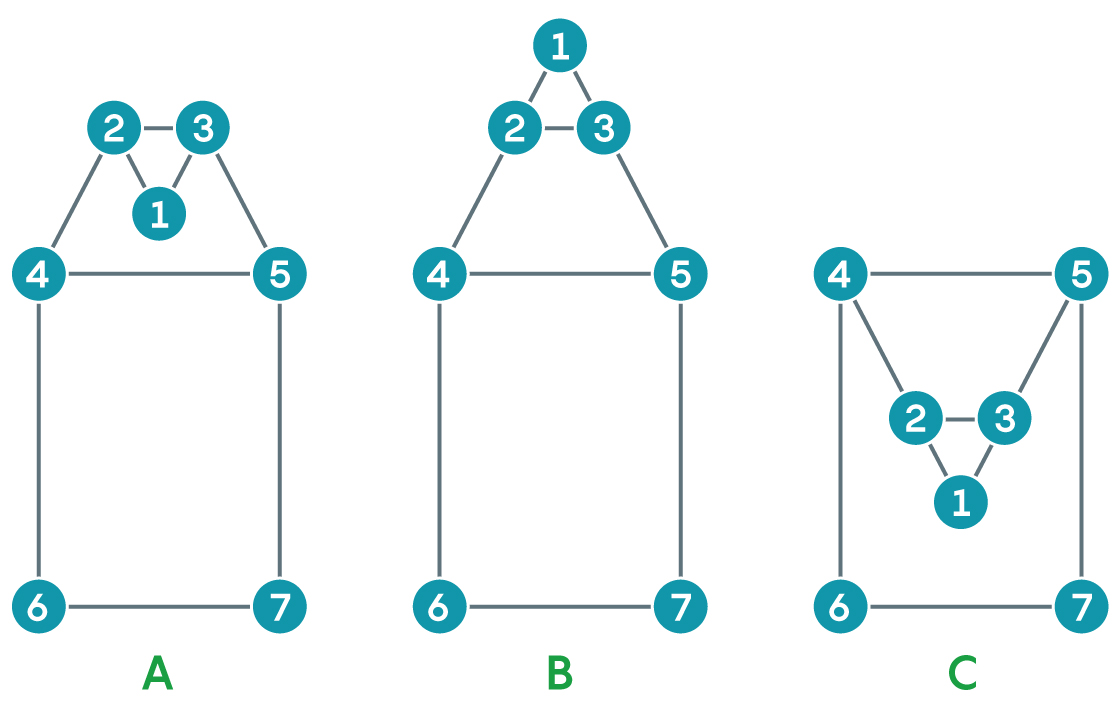
Теперь представьте, что вы хотите вставить новое ребро, соединяющее две вершины планарного графа – допустим, вершины 1 и 6. Для этого вы проводите последовательность переворотов. Из начальной позиции слева за два переворота можно перевести вершину 1 в то место, где её можно соединить с вершиной 6 без пересечения других рёбер.



В работе 2019 года Хольм и Ротенберг обнаружили, что у некоторых рисунков есть больше преимуществ для вставки рёбер, чем у других. Этим «годным» рисункам требуется лишь несколько переворотов для того, чтобы добавить новое ребро, не нарушая планарности.

А вот что они с опозданием осознали в октябре – так это то, что переворот, приближающий вас к позиции, в которой можно добавить новое ребро, также приближает граф к одному из годных рисунков, уже ими определённых. Показав, что последовательность переворотов неизбежно приближает граф к предпочтительным рисункам, можно сделать новый алгоритм, ограничивающий количество переворотов, которое вам может понадобиться для того, чтобы найти способ добавить ребро (если это вообще возможно).

«Мы очень быстро поняли, что с этим новым анализом задачу может решить
крайне простой по концепции алгоритм», — сказал Хольм.


Ева Ротенберг и Якоб Хольм

Новый алгоритм в поисках решения выполняет по одному перевороту за раз. В итоге происходит одно из двух: либо алгоритм находит способ вставить нужное ребро, либо следующий переворот отменяет предыдущий – после чего алгоритм заключает, что добавить новое ребро нет возможности.

«Мы называем этот алгоритм лениво-жадным, — пояснила Ротенберг. – Он проводит только те изменения, которые необходимы для размещения нового ребра».

Их новый метод приближается – но не совпадает – с показателями наилучшего из возможных в принципе алгоритмов для подобных задач. Новому алгоритму тоже приходится проходить через слишком большое число шагов, чтобы его можно было использовать в большинстве реальных приложений – обычно графы бывают достаточно простыми, чтобы их можно было проверить методом полного перебора.

Но для Хольма и Ротенберг скорость работы алгоритма не так важна, как ускорившие его идеи. «Из этого понимания сразу же вытекают следствия», — сказала Ротенберг.

Итальяно считает, что в конечном счёте он сможет найти реальное применение. «Рано или поздно, он наверняка повлияет на то, что находится за пределами информатики с математикой», — сказал он.

Никто не знает, когда могут появиться ещё более быстрые алгоритмы. Это может потребовать совершенно нового прорыва, или же секретный ингредиент уже может где-то существовать, ожидая своего часа в стопке старых исследований.